聚类的肘部法则原理

肘部法则（Elbow Method）是聚类分析中用于确定最佳聚类数（K值） 的常用技术，尤其适用于K-Means等算法。其核心思想是通过分析不同K值下聚类结果的簇内平方和（WCSS, Within-Cluster Sum of Squares） 变化趋势，寻找WCSS下降速率显著放缓的"拐点"（即"肘点"），该点对应的K值即为最佳聚类数。以下从原理、步骤、示意图到代码实现进行完整说明：

一、肘部法则原理

WCSS定义

WCSS是所有样本点到其所属簇中心的距离平方和 ，公式为：
WCSS=∑i=1K∑x∈Ci∥x−μi∥2 \text{WCSS} = \sum_{i=1}^{K} \sum_{x \in C_i} \|x - \mu_i\|^2 WCSS=i=1∑Kx∈Ci∑∥x−μi∥2

其中，CiC_iCi 是第 iii 个簇，μi\mu_iμi 是该簇的质心。
- WCSS越小，表示簇内样本越紧密，聚类效果越好。
K值与WCSS的关系
- 当 K=1K=1K=1 时，WCSS最大（所有样本属于同一簇）。
- 随着 KKK 增加，WCSS逐渐减小（样本被划分到更精细的簇）。
- 当 KKK 超过真实聚类数时，WCSS下降幅度显著降低，形成"肘部"拐点。
"肘点"的意义

拐点处对应的 KKK 值实现了簇内紧密性 与计算效率 的最佳平衡，再增加 KKK 带来的聚类质量提升有限。

二、肘部法则实现步骤

选择K值范围 （如 K=1K=1K=1 到 K=10K=10K=10）。
计算每个K的WCSS ：
- 对每个 KKK 运行K-Means聚类，记录 model.inertia_（即WCSS）。
绘制WCSS-K曲线 ：
- 横轴：KKK 值；纵轴：WCSS值。
识别肘点 ：
- 曲线斜率明显变缓的位置即为最佳 KKK（如下图 K=4K=4K=4 处）。

三、示意图与代码演示

以下代码使用Python的sklearn和matplotlib生成模拟数据并绘制肘部图，最终通过HTML展示结果：

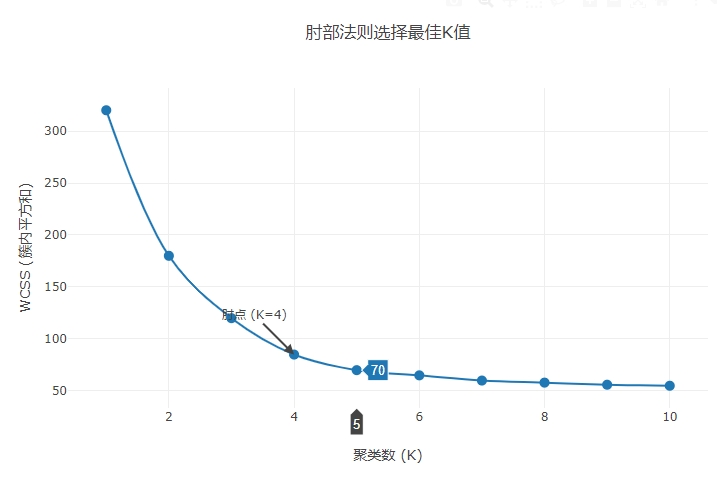
示意图关键点解析

K值	WCSS	趋势分析
K=1	320	最高，样本未分组
K=2→3	180→120	显著下降
K=4	85	拐点（斜率骤减）⭐
K>4	70→55	缓慢下降，收益递减

四、注意事项与局限性

主观性 ：肘点位置可能因数据分布而异，需结合业务解读（如 K=3K=3K=3 或 K=5K=5K=5 均可能合理）。
数据敏感性 ：
- 若曲线无显著拐点（如平稳下降），需结合轮廓系数（Silhouette Score） 验证。
- 复杂结构（多模态分布）可能需更高 KKK 值。
计算优化 ：
- 大数据集可限制 max_iter 或采用MiniBatch K-Means。

五、总结

肘部法则通过量化簇内紧密度随K值的变化 ，为无监督聚类提供了一种直观的评估方式。其核心价值在于平衡模型复杂度 与聚类效果，但需注意：

⚠️ 并非万能：若数据无自然分组（如均匀分布），肘部法则可能失效，此时需依赖领域知识或密度聚类（如DBSCAN）。

实际应用中，建议肘部法则+轮廓系数+业务验证 三者结合，例如在燃气压力分析中，若 K=3K=3K=3 对应"正常/高压故障/低压故障"模式，则优先取 K=3K=3K=3。