数论1.01 - 技术栈

欧几里得（GCD,exGCD）

1.两个数除以最大公约数的结果互为质数

2.欧几里得算法（辗转相除法）求最大公约数

设a,b,c是不全为0的整数，满足1存在整数q, a=bq+c,,那么（a,b）=(b,c)

其中c就等a%b

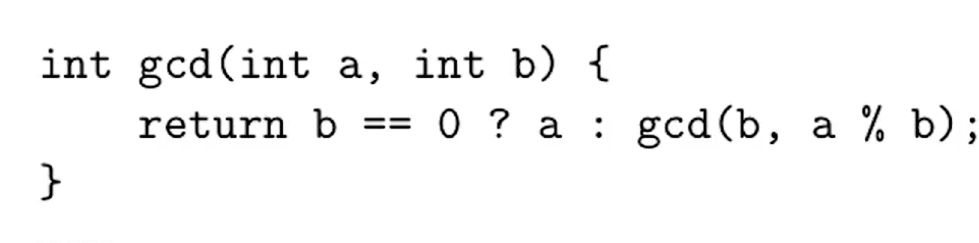
时间复杂度是log的

如果a*m=b*n（a|b*n==m）并且a和b互质，那么a就能整除b*n(其实是a能整除n);

0和任何一个数的最大公约数等于该数本身

至于为什么是下面这个代码咋这么求的：

我以我以及的理解写一遍

第一次：ax+by=gcd;

第二次：bx+(a%b)y=gcd

而a%b=a-a/b*b;

所以b*x+(a-a/b*b)*y=gcd;

bx+ay-a/b*b*y=gcd

ay+b*(x-a/b*y)=gcd;

两个红色字体相比不难看出对应的x,y是谁(从后往前推)

x=y, y=x-a/b*y

如果ax+by=gcd

b=0,那么gcd=a，所以x=1,y=0;

cpp 复制代码

#include<iostream>
#include<cstdio>
#include<cmath>
 
using namespace std;
 
int exgcd(int a,int b,int &x,int &y)//扩展欧几里得算法
{
    if(b==0)
    {
        x=1;y=0;
        return a;  //到达递归边界开始向上一层返回
    }
    int r=exgcd(b,a%b,x,y);
    int temp=y;    //把x y变成上一层的
    y=x-(a/b)*y;
    x=temp;
    return r;     //得到a b的最大公因数
}

整数分解：

埃氏筛：O(nlog(log(n)))

用质数把质数的倍数筛掉

欧拉筛：O（n）

每个合数只需要被其最小的质因子筛掉

cpp 复制代码

const int maxn = 101;   // 表长
int prime[maxn], pNum = 0;    // prime记录素数，pNum记录素数个数 
bool p[maxn] = {false};        // p记录当前数是否被筛去

void eulerSieve(int n)    // 查找记录2-n的素数
{
	for (int i = 2; i <= n; i++)
	{
		if (p[i] == false)  // 如果未被筛过，则为素数
			prime[pNum++] = i;
		for (j = 0; j < pNum; j++)
		{
			if (i * prime[j] > n)      // 当要标记的合数超出范围时跳出
				break;
			p[i * prime[j]] = true;     // 将已经记录的素数的倍数进行标记
			if (i % prime[j] == 0)      //关键步骤
				break;
		}
	}
}

详细解释看这个：欧拉筛详解-CSDN博客挺详细的。