超全面已封装，可直接替换算法！智能算法应用于57个工程应用，CEC2020中57个真实世界问题附完整代码

项目申报小狂人2025-07-30 20:09

表1：57个现实世界中的COPs的详细信息。D是问题的决策变量总数，g是不等式约束的数量，h是等式约束的数量，f(x⃗∗)f(\vec{x}^*)f(x ∗)是已知的最佳可行目标函数值。

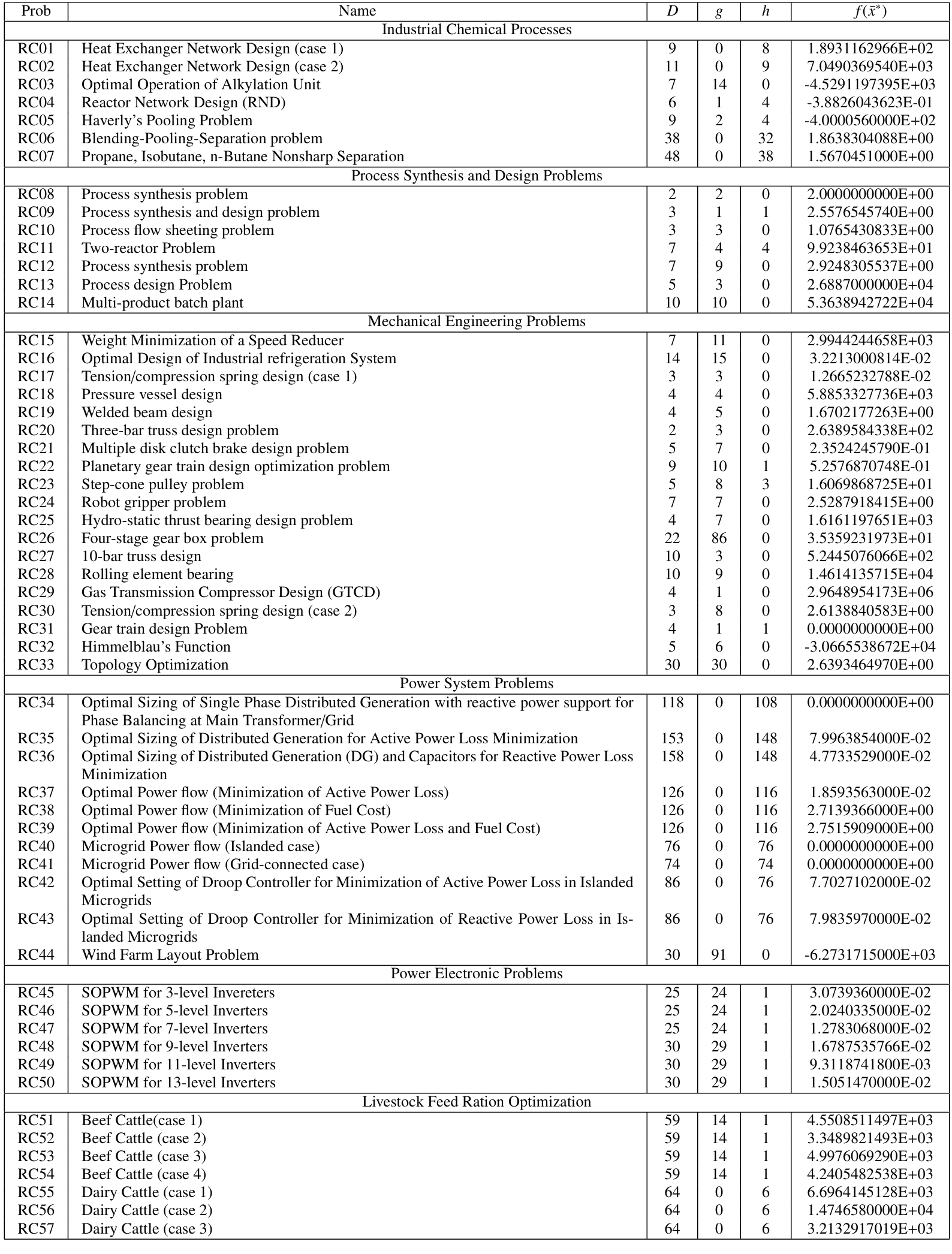
优化问题测试集

编号 问题名称 维度(D) 不等式约束(g) 等式约束(h) 最优解f(x*)
工业化工过程
RC01 换热器网络设计(案例1) 9 0 8 1.8931E+02
RC02 换热器网络设计(案例2) 11 0 9 7.0490E+03
RC03 烷基化单元优化操作 7 14 0 -4.5291E+03
RC04 反应器网络设计(RND) 6 1 4 -3.8826E-01
RC05 Haverly混合池问题 9 2 4 -4.0001E+02
RC06 混合-池化-分离问题 38 0 32 1.8638E+00
RC07 丙烷/异丁烷/正丁烷非精馏分离 48 0 38 1.5670E+00
过程合成与设计
RC08 过程合成问题 2 2 0 2.0000E+00
RC09 过程合成与设计问题 3 1 1 2.5577E+00
RC10 过程流程模拟问题 3 3 0 1.0765E+00
RC11 双反应器问题 7 4 4 9.9238E+01
RC12 过程合成问题 7 9 0 2.9248E+00
RC13 过程设计问题 5 3 0 2.6887E+04
RC14 多产品批次工厂 10 10 0 5.3639E+04
*机械工程问题
RC15 减速器重量最小化 7 11 0 2.9944E+03
RC16 工业制冷系统优化设计 14 15 0 3.2213E-02
RC17 拉伸/压缩弹簧设计(案例1) 3 3 0 1.2665E-02
RC18 压力容器设计 4 4 0 5.8853E+03
RC19 焊接梁设计 4 5 0 1.6702E+00
RC20 三杆桁架设计 2 3 0 2.6389E+02
RC21 多盘离合器制动设计 5 7 0 2.3524E-01
RC22 行星齿轮系优化设计 9 10 1 5.2577E-01
RC23 阶梯锥滑轮问题 5 8 3 1.6070E+01
RC24 机器人夹持器问题 7 7 0 2.5288E+00
RC25 静压推力轴承设计 4 7 0 1.6161E+03
RC26 四级齿轮箱问题 22 86 0 3.5359E+01
RC27 10杆桁架设计 10 3 0 5.2445E+02
RC28 滚动轴承设计 10 9 0 1.4614E+04
RC29 气体传输压缩机设计(GTCD) 4 1 0 2.9649E+06
RC30 拉伸/压缩弹簧设计(案例2) 3 8 0 2.6139E+00
RC31 齿轮系设计问题 4 1 1 0.0000E+00
RC32 Himmelblau函数优化 5 6 0 -3.0666E+04
RC33 拓扑优化问题 30 30 0 2.6393E+00
电力系统问题
RC34 配电网单相分布式发电优化配置(含无功支撑) 118 0 108 0.0000E+00
RC35 有功损耗最小的分布式发电优化配置 153 0 148 7.9964E-02
RC36 无功损耗最小的DG与电容器优化配置 158 0 148 4.7734E-02
RC37 最优潮流(有功损耗最小) 126 0 116 1.8594E-02
RC38 最优潮流(燃料成本最小) 126 0 116 2.7139E+00
RC39 最优潮流(有功损耗与燃料成本最小) 126 0 116 2.7516E+00
RC40 微电网潮流(孤岛模式) 76 0 76 0.0000E+00
RC41 微电网潮流(并网模式) 74 0 74 0.0000E+00
RC42 孤岛微电网有功损耗最小的下垂控制优化 86 0 76 7.7027E-02
RC43 孤岛微电网无功损耗最小的下垂控制优化 86 0 76 7.9836E-02
RC44 风电场布局优化 30 91 0 -6.2732E+03
电力电子问题
RC45 3电平逆变器SOPWM优化 25 24 1 3.0739E-02
RC46 5电平逆变器SOPWM优化 25 24 1 2.0240E-02
RC47 7电平逆变器SOPWM优化 25 24 1 1.2783E-02
RC48 9电平逆变器SOPWM优化 30 29 1 1.6788E-02
RC49 11电平逆变器SOPWM优化 30 29 1 9.3119E-03
RC50 13电平逆变器SOPWM优化 30 29 1 1.5051E-02
畜牧饲料配比优化
RC51 肉牛饲料优化(案例1) 59 14 1 4.5509E+03
RC52 肉牛饲料优化(案例2) 59 14 1 3.3490E+03
RC53 肉牛饲料优化(案例3) 59 14 1 4.9976E+03
RC54 肉牛饲料优化(案例4) 59 14 1 4.2405E+03
RC55 奶牛饲料优化(案例1) 64 0 6 6.6964E+03
RC56 奶牛饲料优化(案例2) 64 0 6 1.4747E+04
RC57 奶牛饲料优化(案例3) 64 0 6 3.2133E+03

完整代码

matlab 复制代码 
clear all
close all
clc

format longG
T = 1000;
ProN = 3;
N = 50;

for i = 1:ProN
    disp(['======= Problems: ',num2str(i)]);
    [lb,ub,dim,fobj] = Problem_Define(i);
    [SDECOA_fMin,SDECOA_bestX,SDECOA_curve] = SDECOA(N,T,lb,ub,dim,fobj);
    figure(i);
    plot(SDECOA_curve,'b--','LineWidth',1.5,'MarkerIndices',1:ceil(T/10):T);
end
matlab 复制代码 
function [par] = Cal_par(prob_k)
	% CEC2020 Constrained Optimization Test Suite 
	% Abhishek Kumar (email: abhishek.kumar.eee13@iitbhu.ac.in, Indian Institute of Technology (BHU), Varanasi) 
	
	% prob_k -> Index of problem.
	% par.n  -> Dimension of the problem.
	% par.g  -> Number of inequility constraints.
	% par.h  -> Number of equality constraints.
	% par.xmin -> lower bound of decision variables.
	% par.xmax -> upper bound of decision variables.
	
	
	D        = [9	11	7	6	9	38	48	2	3	3	7	7	5	10	7	14	3	4	4	2	5	9	5	7	4	22	10	10	4	3	4	5	...
	            30	118	153	158	126	126	126	76	74	86	86	30	25	25	25	30	30	30	59	59	59	59	64	64	64];
	par.n    = D(prob_k);     
	gn       = [0,0,14,1,2,0,0,2,1,3,4,9,3,10,11,15,3,4,5,3,7,10,8,7,7,86,3,9,1,8,1,6,30,0,0,0,0,0,0,0,0,0,0,105,24,24,24,29,29,29,14,14,14,14,0,0,0];
	hn       = [8,9,0,4,4,32,38,0,1,0,4,0,0,0,0,0,0,0,0,0,0,1,3,0,0,0,0,0,0,0,1,0,0,108,148,148,116,116,116,76,74,76,76,0,1,1,1,1,1,1,1,1,1,1,6,6,6];
	par.gn    = gn;
	par.hn    = hn;
	par.g     = gn(prob_k);
	par.h     = hn(prob_k);
	%% range
	% bound constraint definitions for all 18 test functions
	xmin1    = [0,0,0,0,1000,0,100,100,100];
	xmax1    = [10,200,100,200,2000000,600,600,600,900];
	xmin2    = [10^4,10^4,10^4,0,0,0,100,100,100,100,100];
	xmax2    = [0.819*10^6, 1.131*10^6, 2.05*10^6,0.05074,0.05074,0.05074,200,300,300,300,400];
	xmin3    = [1000,0,2000,0,0,0,0];
	xmax3    = [2000,100,4000,100,100,20,200];
	xmin4    = [0,0,0,0,1e-5,1e-5];
	xmax4    = [1,1,1,1,16,16];
	xmin5    = -0*ones(1,par.n);
	xmax5    = [100,200,100,100,100,100,200,100,200];
	xmin6    = 0*ones(1,par.n);
	xmax6    = [90,150,90,150,90,90,150,90,90,90,150,150,90,90,150,90,150,90,150,90,1,1.2,1,1,1,0.5,1,1,0.5,0.5,0.5,1.2,0.5,1.2,1.2,0.5,1.2,1.2];
	xmin7    = -0*ones(1,par.n); xmin7([24,26,28,31]) = 0.849999;
	xmax7    = 1*ones(1,par.n); xmax7(4) = 140; xmax7([25,27,32,35,37,29]) = 30;xmax7([2,3,5,13,14,15]) = 90; xmax7([1,6,7,8,9,10,11,12,16,17,18,19,20]) = 35;
	xmin8    = [0,-0.51];
	xmax8    = [1.6,1.49];
	xmin9    = [0.5,0.5,-0.51];
	xmax9    = [1.4,1.4,1.49];
	xmin10   = [0.2, -2.22554, -0.51];
	xmax10   = [1, -1, 1.49];
	xmin11   = [0,0,0,0,-0.51,-0.51,0];
	xmax11   = [20,20,10,10,1.49,1.49,40];
	xmin12   = [0,0,0,-0.51,-0.51,-0.51,-0.51];
	xmax12   = [100,100,100,1.49,1.49,1.49,1.49]; 
	xmin13   = [27,27,27,77.51,32.51];
	xmax13   = [45,45,45,102.49,45.49];
	xmin14   = [ 0.51,0.51,0.51,250,250,250,6,4,40,10];
	xmax14   = [3.49,3.49,3.49,2500,2500,2500,20,16,700,450];
	xmin15   = [2.6, 0.7, 17, 7.3, 7.3, 2.9, 5];
	xmax15   = [3.6, 0.8, 28, 8.3, 8.3, 3.9, 5.5];
	xmin16   = 0.001*ones(1,par.n);
	xmax16   = +5*ones(1,par.n);
	xmin17   = [0.05,0.25,2.00];
	xmax17   = [2,1.3,15.0];
	xmin18   = [0.51,0.51,10,10];
	xmax18   = [99.49,99.49,200,200];
	xmin19   = [0.125,0.1,0.1,0.1];
	xmax19   = [2,10,10,2];
	xmin20   = 0*ones(1,par.n);
	xmax20   = 1*ones(1,par.n); 
	xmin21   = [60,90,1,0,2];
	xmax21   = [80,110,3,1000,9];
	xmin22   = [16.51,13.51,13.51,16.51,13.51,47.51,0.51,0.51,0.51];
	xmax22   = [96.49,54.49,51.49,46.49,51.49,124.49,3.49,6.49,6.49];
	xmin23   = [0,0,0,0,0];
	xmax23   = [60,60,90,90,90];
	xmin24   = [10,10,100,0,10,100,1];
	xmax24   = [150,150,200,50,150,300,3.14];
	xmin25   = [ 1, 1,  1e-6,1];
	xmax25   = [16, 16, 16*1e-6,16];
	xmin26   = [ 6.51.*ones(1,8), 0.51.*ones(1,14)];
	xmax26   = [ 76.49.*ones(1,8), 4.49.*ones(1,4), 9.49.*ones(1,10)];
	xmin27   = 0.645e-4*ones(1,par.n);
	xmax27   = 50e-4*ones(1,par.n); 
	xmin28   = [125,10.5,4,0.515,0.515,0.4,0.6,0.3,0.02,0.6];
	xmax28   = [150,31.5,50,0.6,0.6,0.5,0.7,0.4,0.1,0.85];
	xmin29   = [20,1,20,0.1];
	xmax29   = [50,10,50,60];
	xmin30   = [0.51,0.6,0.51];
	xmax30   = [70.49,3,42.49];
	xmin31   = 12.*ones(1,4);
	xmax31   = 60.*ones(1,4);
	xmin32   = [78,33,27,27,27];
	xmax32   = [102,45,45,45,45];
	xmin33   = 0.001.*ones(1,par.n);
	xmax33   = ones(1,par.n);
	xmin34   = -1*ones(1,par.n);
	xmax34   = +1*ones(1,par.n);
	xmin35   = -1*ones(1,par.n);
	xmax35   = +1*ones(1,par.n);
	xmin36   = -1*ones(1,par.n);
	xmax36   = +1*ones(1,par.n);
	xmin37   = -1*ones(1,par.n);xmin37(117:126) = 0;
	xmax37   = +1*ones(1,par.n);
	xmin38   = -1*ones(1,par.n);xmin38(117:126) = 0;
	xmax38   = +1*ones(1,par.n);
	xmin39   = -1*ones(1,par.n);xmin39(117:126) = 0;
	xmax39   = +1*ones(1,par.n);
	xmin40   = -1*ones(1,par.n);xmin40(75:76) = 0;
	xmax40   = +1*ones(1,par.n);xmax40(75:76) = 2;
	xmin41   = -1*ones(1,par.n);
	xmax41   = +1*ones(1,par.n);
	xmin42   = -1*ones(1,par.n);xmin42(75:76) = 0;xmin42(77:86) = 0;
	xmax42   = +1*ones(1,par.n);xmax42(75:76) = 2;xmax42(77:86) = 500;
	xmin43   = -1*ones(1,par.n);xmin43(75:76) = 0;xmin43(77:86) = 0;
	xmax43   = +1*ones(1,par.n);xmax43(75:76) = 2;xmax43(77:86) = 500;
	xmin44   = 40*ones(1,par.n);
	xmax44   = 1960*ones(1,par.n);
	xmin45   = -0*ones(1,par.n);
	xmax45   = +90*ones(1,par.n);
	xmin46   = -0*ones(1,par.n);
	xmax46   = +90*ones(1,par.n);
	xmin47   = -0*ones(1,par.n);
	xmax47   = +90*ones(1,par.n);
	xmin48   = -0*ones(1,par.n);
	xmax48   = +90*ones(1,par.n);
	xmin49   = -0*ones(1,par.n);
	xmax49   = +90*ones(1,par.n);
	xmin50   = -0*ones(1,par.n);
	xmax50   = +90*ones(1,par.n);
	xmin51   = 0.*ones(1,par.n);
	xmax51   = 10.*ones(1,par.n);
	xmin52   = 0.*ones(1,par.n);
	xmax52   = 10.*ones(1,par.n);
	xmin53   = 0.*ones(1,par.n);
	xmax53   = 10.*ones(1,par.n);
	xmin54   = 0.*ones(1,par.n);
	xmax54   = 10.*ones(1,par.n);
	xmin55   = 0.*ones(1,par.n);
	xmax55   = 10.*ones(1,par.n);
	xmin56   = 0.*ones(1,par.n);
	xmax56   = 10.*ones(1,par.n);
	xmin57   = 0.*ones(1,par.n);
	xmax57   = 10.*ones(1,par.n);
	
	eval(['par.xmin=xmin' int2str(prob_k) ';']);
	eval(['par.xmax=xmax' int2str(prob_k) ';' ]);
end
相关推荐
励志成为糕手11 分钟前
编程语言Java——核心技术篇（五）IO流：数据洪流中的航道设计
java·开发语言·性能优化
世界emm1 小时前
Python 脚本：获取公网 IPv4 和 IPv6 地址
开发语言·python
慕y2741 小时前
Java学习第八十四部分——HttpClient
java·开发语言·学习
Bruce-li__2 小时前
Python多线程利器：重入锁（RLock）详解——原理、实战与避坑指南
开发语言·python
用户3074596982072 小时前
《PHP属性详解：从基础到只读的完全指南》
后端·php
用户3074596982072 小时前
《PHP类的基础概念：从零开始学面向对象》
后端·php
程序员编程指南2 小时前
Qt 移动应用常见问题与解决方案
c语言·开发语言·c++·qt
kebeiovo2 小时前
C++代码题部分（1）
开发语言·c++
tomato092 小时前
河南萌新联赛2025第（二）场：河南农业大学（补题）
开发语言·c++
双力臂4043 小时前
Java注解与反射：从自定义注解到框架设计原理
java·开发语言
热门推荐
01Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code02全球最强模型Grok4，国内已可免费使用！（附教程）03Coze 开源了，送上保姆级私有化部署方案【建议收藏】04MSPM0G3507——读取引脚的高低电平方法（数字信号循迹模块）05腾讯还是太全面了，限时免费！超全CodeBuddy IDE保姆级教程！（附案例）06扣子开源本地部署教程 丨Coze智能体小白喂饭级指南07KGG转MP3工具|非KGM文件|解密音频08机器学习——多项式回归算法09【手把手攻略】国家育儿补贴正式开领！一键算清你能拿多少钱？附补贴领取计算器10coze 开源版本地部署及踩过的坑【喂饭级教程】