河南萌新联赛2025第（二）场：河南农业大学（补题）

文章目录

• 前言
• A.约数个数和
• • 整除分块(相当于约数求和)
  • • 相关例题：取模
• B.异或期望的秘密
• • 二进制的规律
  • • 相关例题
    • • 累加器
      • 小蓝的二进制询问
  • 乘法逆元
  • • [1. 概念](#1. 概念)
    • 2.基本定义
    • 3.费马小定理
    • • 1.定理内容
      • 2.重要推论
• D.开罗尔网络的备用连接方案
• E.咕咕嘎嘎!!!(easy)
• I.猜数游戏(easy)
• K.打瓦
• M.米娅逃离断头台
• 总结

前言

依旧是只会写签到题的一场。

---

A.约数个数和

题目传送门：约数个数和

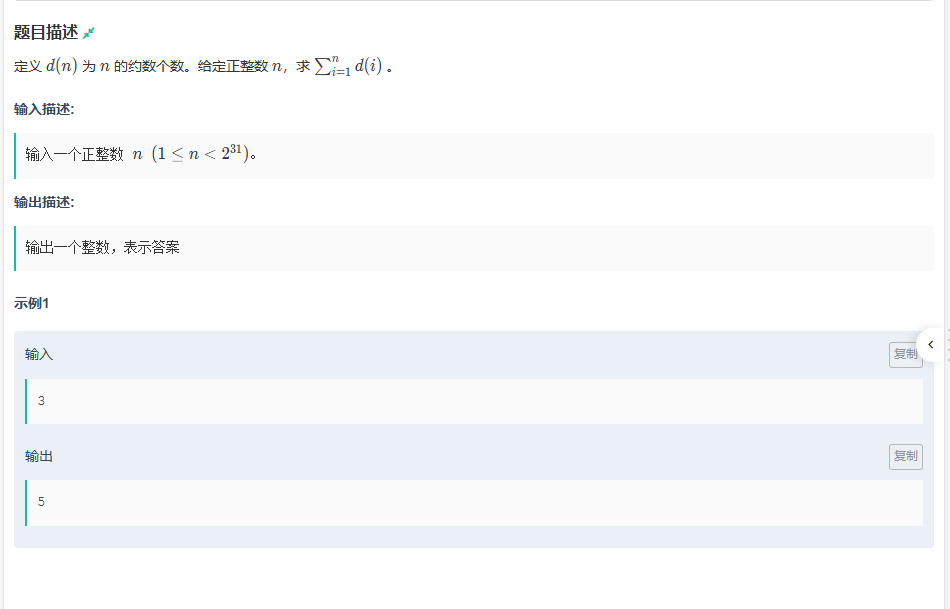
这一题利用到了整除分块，如果不这样的话，数据太大，会时间超限。

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll ans=0;
void solve()
{
	ll n;
	cin>>n;
    for(ll l=1,r;l<=n;l=r+1)
    {
        r=n/(n/l);
        ans+=(n/l)*(r-l+1);
    }
    cout<<ans<<endl;
}
signed main()
{
	IOS;
	ll t=1;
	//cin>>t;
	while(t--)
	solve();
	return 0;
	}

整除分块(相当于约数求和)

介绍：整除分块（也叫数论分块）是数论和算法竞赛中常用的优化技巧，主要用于高效计算形如
∑ i = 1 n f ( i ) ⋅ g ( ⌊ n i ⌋ ) \sum_{i=1}^n f(i) \cdot g\left(\left\lfloor \frac{n}{i} \right\rfloor\right) i=1∑nf(i)⋅g(⌊in⌋) 的求和式，核心思想是利用「整除的周期性」，将求和式中结果相同的区间合并，减少计算次数。
一、整除分块的核心原理 ：

利用整除的「周期性」对于固定的 n，当 i 从 1 到 n 变化时， ⌊ n i ⌋ \left\lfloor \frac{n}{i} \right\rfloor ⌊in⌋ 的值会分段相同。

例如：(n=10) 时， ⌊ 10 i ⌋ \left\lfloor \frac{10}{i} \right\rfloor ⌊i10⌋ 的取值如下：

可以看到， ⌊ n i ⌋ \left\lfloor \frac{n}{i} \right\rfloor ⌊in⌋ 的值会形成连续的区间段（如 i=4,5 时，值都是 2； i = 6 ∼ 10 i=6\sim10 i=6∼10时，值都是 1）。关键发现：

对于某个值 k = ⌊ n i ⌋ k = \left\lfloor \frac{n}{i} \right\rfloor k=⌊in⌋，所有能使 ⌊ n i ⌋ = k \left\lfloor \frac{n}{i} \right\rfloor = k ⌊in⌋=k的 i 会构成一个连续区间 ([l, r])，其中：左端点 l 是当前区间的起始右端点 r 满足：
r = ⌊ n k ⌋ = ⌊ n ⌊ n l ⌋ ⌋ r = \left\lfloor \frac{n}{k} \right\rfloor = \left\lfloor \frac{n}{\left\lfloor \frac{n}{l} \right\rfloor} \right\rfloor r=⌊kn⌋=⌊⌊ln⌋n⌋

利用这一性质，我们可以将原本需要遍历 n 次的求和，优化为遍历所有不同的 k 对应的区间段， 时间复杂度从 O ( n ) 降到 O ( n ) （因为不同的 k 最多有 2 n 个） 时间复杂度从 O(n) 降到 O(\sqrt{n})（因为不同的 k 最多有 2\sqrt{n} 个） 时间复杂度从O(n)降到O(n )（因为不同的k最多有2n 个）。
模板：

long long sum = 0;
for (int l = 1, r; l <= n; l = r + 1) {
    int k = n / l;
    r = n / k;  // 计算当前段的右端点
    sum += (r - l + 1) * k;
}

相关例题：取模

题目传送门：取模

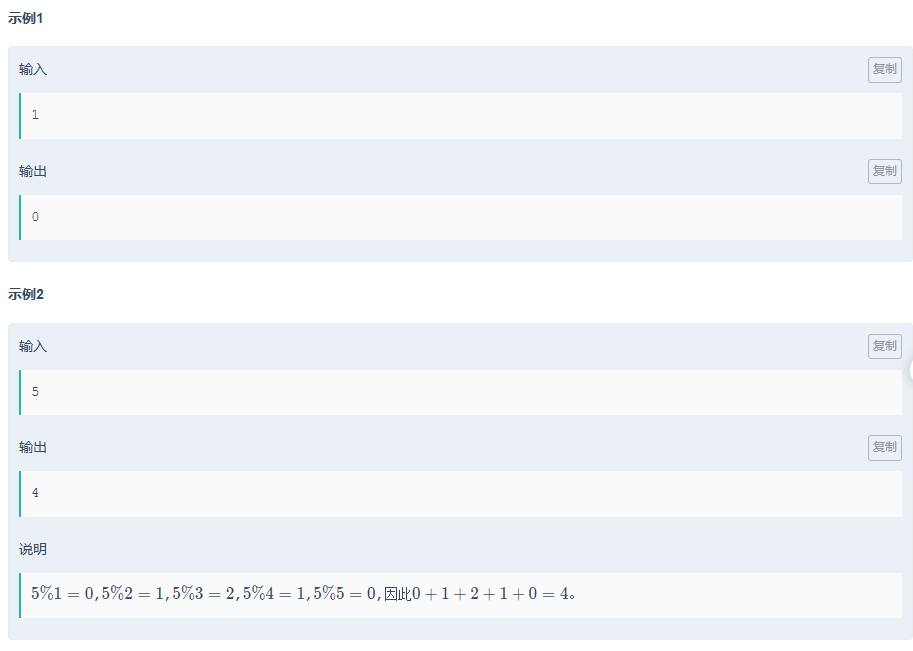
对于这一题，同样可以通过一系列推理，将其转换到整除分块

利用取模的数学定义：
n % i = n − i ⋅ ⌊ n i ⌋ n \% i = n - i \cdot \left\lfloor \frac{n}{i} \right\rfloor n%i=n−i⋅⌊in⌋因此，原求和式可展开为：
∑ i = 1 n ( n % i ) = ∑ i = 1 n ( n − i ⋅ ⌊ n i ⌋ ) \sum_{i=1}^n \left( n \% i \right) = \sum_{i=1}^n \left( n - i \cdot \left\lfloor \frac{n}{i} \right\rfloor \right) i=1∑n(n%i)=i=1∑n(n−i⋅⌊in⌋)拆分求和式：
∑ i = 1 n ( n % i ) = ∑ i = 1 n n − ∑ i = 1 n ( i ⋅ ⌊ n i ⌋ ) \sum_{i=1}^n \left( n \% i \right) = \sum_{i=1}^n n - \sum_{i=1}^n \left( i \cdot \left\lfloor \frac{n}{i} \right\rfloor \right) i=1∑n(n%i)=i=1∑nn−i=1∑n(i⋅⌊in⌋)

对于i求和，可以通过等差数列求和推理出来

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll mod=998244353;
void solve()
{
	ll n;
	cin>>n;
	__int128 ans=0;//特别注意类型，因为数据范围非常大
	for(__int128 l=1,r;l<=n;l=r+1)
	{
		ll k=n/l;
		r=n/k;
		ans+=k*((r-l+1)*(r-l)/2+(r-l+1)*l)%mod;
	}
    ll an=((__int128)n*(__int128)n-ans)%mod;
	cout<<an<<endl;
}
signed main()
{
	IOS;
	ll t=1;
	// cin>>t;
	while(t--)
	solve();
	return 0;
}

B.异或期望的秘密

题目传送门：异或期望的秘密

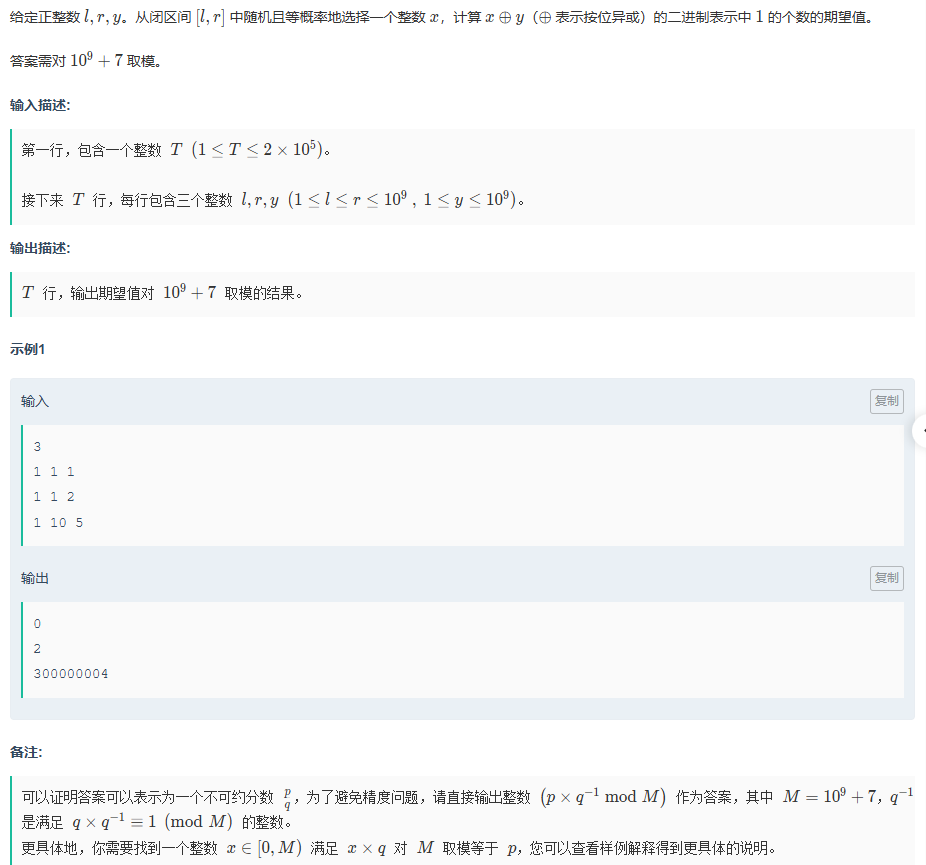
这一题用到的知识就很多了，有关于二进制的规律，以及乘法逆元，还有数学期望的计算；

思路：

通过数据范围可以发现，直接进行循环肯定会时间超限，为此就有了一个很妙的方法，利用到异或以及二进制的规律，通过遍历y在bitset的每一位，通过当前y在二进制下的0与1，与L到R之间相同位数下的1的个数来进行判断，由于异或的性质，相同为0，由此来反着推出贡献为1的总数，最后再通过乘法逆元。

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll mod=1e9+7;
ll qmod(ll x,ll y)//乘法逆元（快速幂）
{
	ll sum=1;
	while(y)
	{
		if(y&1)
		{
			sum*=x;
			sum%=mod;
		}
		x*=x;
		x%=mod;
		y>>=1;
	}
	return sum;
}
ll f(ll x,ll i)//计算x第i位的1的个数
{
	if(x==0)
	return 0;
	ll sum=0;
	ll val=1ll<<i;//每个周期的贡献值
	ll curr=1ll<<(i+1);//一个周期的大小
	ll re=x%curr-val+1;//计算不足一个周期的贡献值
	sum+=val*(x/curr);//计算整周期的贡献
    sum+= max((ll)0,re);//比较剩余周期是否有贡献值
	sum%=mod;
	return sum;
}
void solve()
{
	ll l,r,y;
	cin>>l>>r>>y;
	ll k=r-l+1;
	ll ans=0;
	bitset<31>m(y);//方便进行异或
	for(ll i=0;i<=29;i++)
	{
		ll num=f(r,i)-f(l-1,i);//计算当前位数的区间1的个数总和
		if(m[i]==1)
		num=k-num;//贡献为0的反推出贡献为1的
		ans+=num;
		ans%=mod;
	}
	
	cout<<(ans*qmod(k,mod-2))%mod<<endl;//乘法逆元
}
signed main()
{
	IOS;
	ll t=1;
	cin>>t;
	while(t--)
	solve();
	return 0;
}

二进制的规律

1 ------ 00001

2 ------ 00010

3 ------ 00011

4 ------ 00100

5 ------ 00101

6 ------ 00110

7 ------ 00111

8 ------ 01000

9 ------ 01001

10 ------01010

11 ------ 01011

12 ------ 01100

13 ------ 01101

14 ------ 01110

15 ------ 01111

16 ------ 10000

17 ------ 10001

18 ------ 10010

19 ------ 10011

20 ------ 10100

通过观察会发现，每一位的周期就是权值的2倍，而权值又是该当前位数的
(2ⁱ ) ,注意位数i是从0开始的，故而周期为2ⁱ⁺¹ .

至于求余数的贡献值时，会发现在周期的一半的前一位值是1，故而需要多加上1，因为其是余数减去一半的周期。

关键点：

    if(x==0)
	return 0;
	ll sum=0;
	ll val=1ll<<i;//每个周期的贡献值
	ll curr=1ll<<(i+1);//一个周期的大小
	ll re=x%curr-val+1;//计算不足一个周期的贡献值
	sum+=val*(x/curr);//计算整周期的贡献
    sum+= max((ll)0,re);//比较剩余周期是否有贡献值

相关例题

累加器

题目传送门：累加器

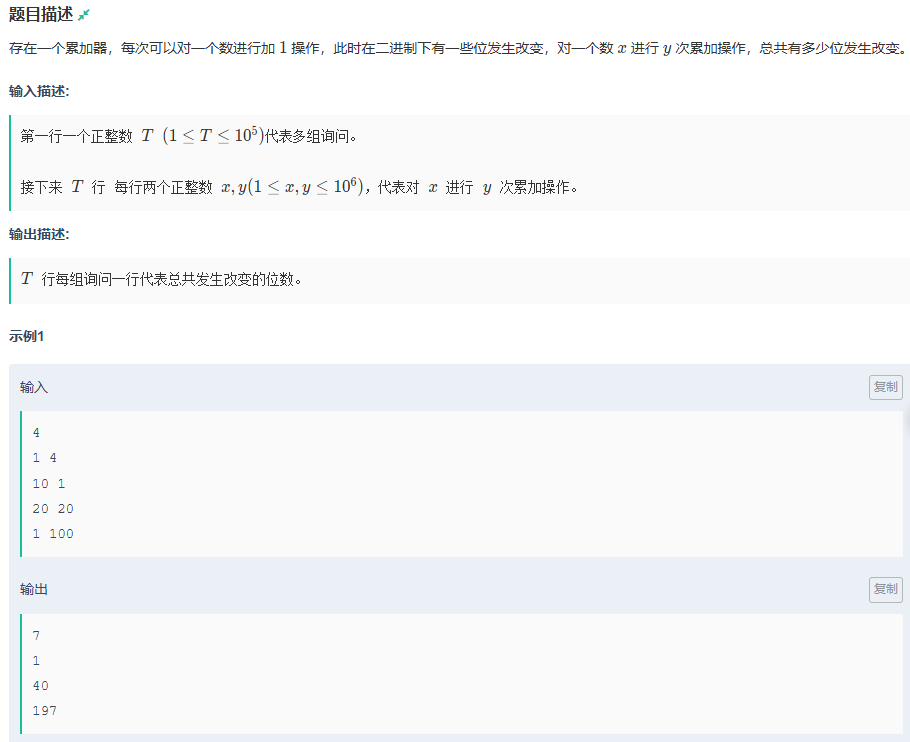
通过观察样例会发现，每位改变的位数，都与当前的2的位数次方

AC代码;

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
const ll N=1e6+10;
ll f(ll x)//进行前缀和
{
	ll sum=0;
	ll y=log2(x);
	for(ll i=0;i<y;i++)
	{
		ll k=(ll)pow(2,i);//关键规律
		sum+=x/k;
	}
	return sum;
}
void solve()
{
	ll x,y;
	cin>>x>>y;
	cout<<f(x+y)-f(x)<<endl;
}
signed main()
{
	IOS;
	ll t=1;
	cin>>t;
	while(t--)
	solve();
	return 0;
}

小蓝的二进制询问

题目传送门：小蓝的二进制询问

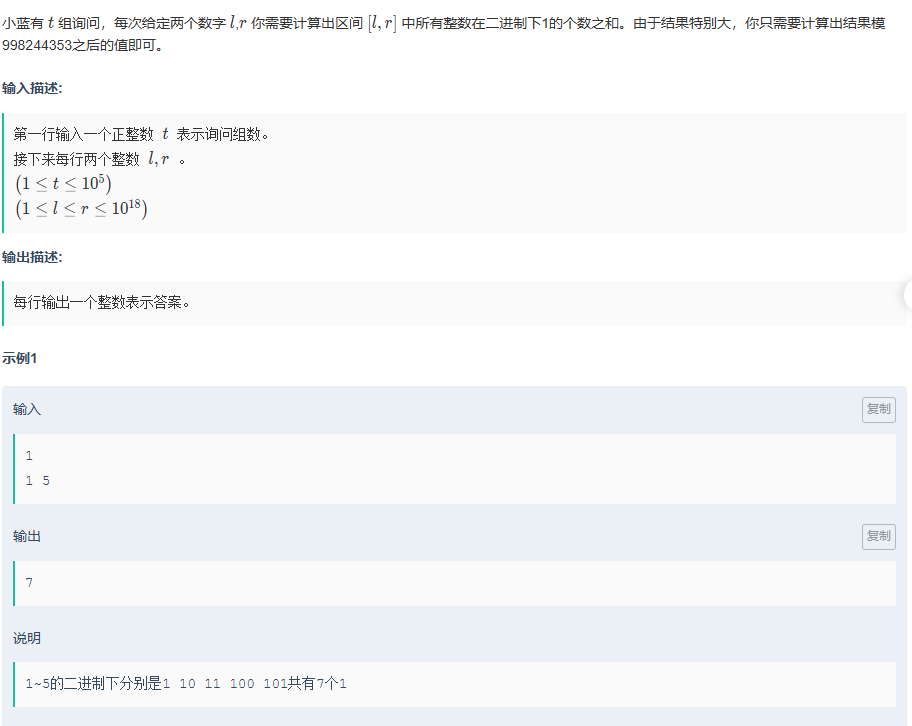
这一题便是之前的规律了；

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
const ll N=1e6+10;
const ll mod=998244353;
ll f(ll x)
{
	ll sum=0;
    ll y=log2(x)+1;//计算当前的位数
    if(x==0)
        return 0;
    ll val=1;
	for(ll i=0;i<=y;i++)
    {
        val=1ll<<i;//权值
        ll curr=val*2;//周期
        sum+=val*(x/curr);//完整周期总和
        ll re=x%curr-val+1;//剩余周期的贡献
        sum+=max((ll)0,re);//判断是否有贡献
        sum%=mod;
    }
	return sum%mod;
}
void solve()
{
	ll x,y;
	cin>>x>>y;
	cout<<(f(y)-f(x-1)+mod)%mod<<endl;
}
signed main()
{
	IOS;
	ll t=1;
	cin>>t;
	while(t--)
	solve();
	return 0;
}

乘法逆元

1. 概念

在数学中，乘法逆元是一个与乘法运算相关的重要概念，它描述了两个数之间的一种特殊关系。简单来说，对于给定的数 a，如果存在另一个数 b，使得它们的乘积等于乘法单位元（通常是 1），那么 b 就被称为 a 的乘法逆元。

2.基本定义

设 a 是一个数（或更广泛的代数结构中的元素），若存在数 b 满足： a × b = b × a = 1 a \times b = b \times a = 1 a×b=b×a=1

则称 b 是 a 的乘法逆元，记作 b = a − 1 b = a^{-1} b=a−1（读作 "a 的逆"）。这里的 "1" 是乘法单位元，即与任何数相乘都不改变该数的特殊元素（例如整数乘法中，1 就是单位元）。

3.费马小定理

1.定理内容

若 p 是一个质数，且整数 a 不是 p 的倍数 （即 a 与 p 互质， gcd ⁡ ( a , p ) = 1 ) （即 a 与 p 互质，\gcd(a, p) = 1) （即a与p互质，gcd(a,p)=1)，

则有： a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \pmod{p} ap−1≡1(modp)

符号解释： ≡ ( m o d p ) 表示"模 p 同余"，即 a p − 1 除以 p 的余数等于 1 。 \equiv \pmod{p}表示 "模 p 同余"，即 a^{p-1}除以 p 的余数等于 1。 ≡(modp)表示"模p同余"，即ap−1除以p的余数等于1。

2.重要推论

费马小定理的一个关键应用是求模运算中的乘法逆元。

由定理 a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \pmod{p} ap−1≡1(modp)

变形可得： a × a p − 2 ≡ 1 ( m o d p ) a \times a^{p-2} \equiv 1 \pmod{p} a×ap−2≡1(modp)

这表明：当 p 是质数且 a 与 p 互质时， a p − 2 m o d    p a^{p-2} \mod p ap−2modp

就是 a 模 p 的乘法逆元 （即 a − 1 ≡ a p − 2 ( m o d p ) ） （即 a^{-1} \equiv a^{p-2} \pmod{p}） （即a−1≡ap−2(modp)）。

根据费马小定理，当 p 是质数且 gcd ⁡ ( a , p ) = 1 时 \gcd(a, p) = 1时 gcd(a,p)=1时，

有： a p − 1 ≡ 1 ( m o d p ) a^{p-1} \equiv 1 \pmod{p} ap−1≡1(modp)

将等式左边因式分解 （把 a p − 1 拆成 a × a p − 2 ），得到： a × a p − 2 ≡ 1 ( m o d p ) （把 a^{p-1} 拆成 a \times a^{p-2} ），得到：a \times a^{p-2} \equiv 1 \pmod{p} （把ap−1拆成a×ap−2），得到：a×ap−2≡1(modp)

D.开罗尔网络的备用连接方案

题目传送门：开罗尔网络的备用连接方案

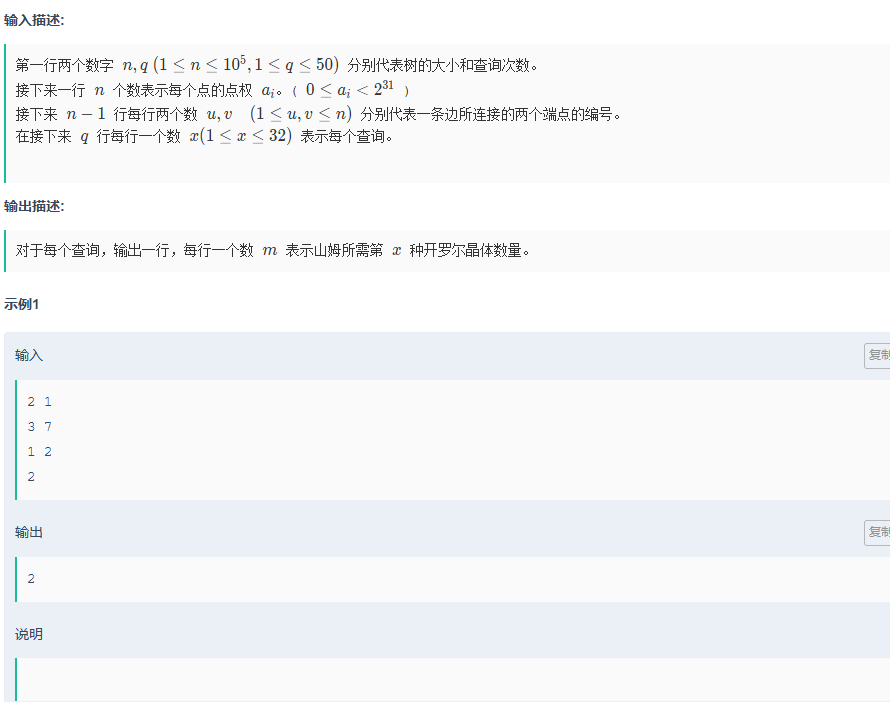
通过题目，可以发现就是一个加权无向图，来求取经过按位与之后该数二进制下1的个数，

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e5+10;
vector<ll> p[N];//用来存边
ll a[N];//存该节点的权值
ll ans[N];//保存种类数目
void dfs(ll x,ll w,ll f)
{
    ll c=a[x]&w;//每次都进行按位与
    bitset<40>b(c);//为了更好的求1的个数
    ans[b.count()]++;//统计种类
    for(ll i:p[x])
    {
        if(i!=f)//防止重边也就是防止一个节点遍历两次
        {
            dfs(i,c,x);//继续往下搜索i代表的是子节点，c则是要更新的值，x则代表的是父节点
        }
    }
}
void solve()
{
    ll n,q;
    cin>>n>>q;
    for(ll i =1;i<=n;i++)
        cin>>a[i];
    for(ll i=1;i<n;i++)
    {
        ll x,y;
        cin>>x>>y;
        p[x].push_back(y);//存边，即双向边
        p[y].push_back(x);
    }
    dfs(1,-1,0);//从节点1开始进行搜索
        while(q--)
        {
            ll x;
            cin>>x;
            cout<<ans[x]<<endl;
        }
}
signed main()
{
    IOS;
    ll t=1;
    //cin>>t;
    while(t--)
        solve();
    return 0;
}

E.咕咕嘎嘎!!!(easy)

题目传送门：咕咕嘎嘎!!!(easy)

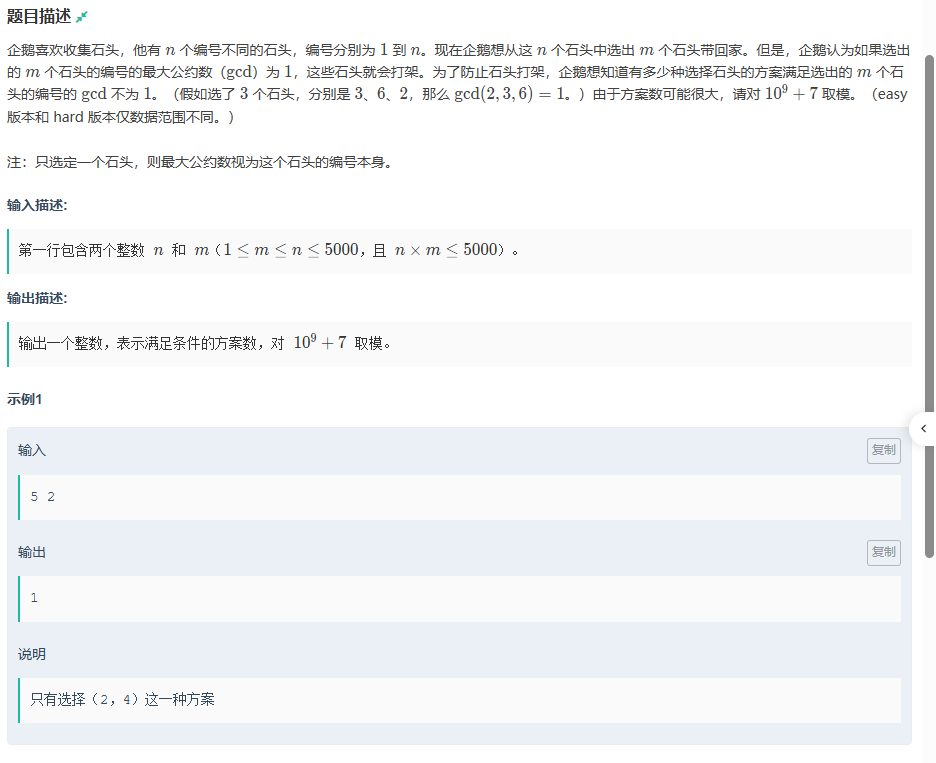
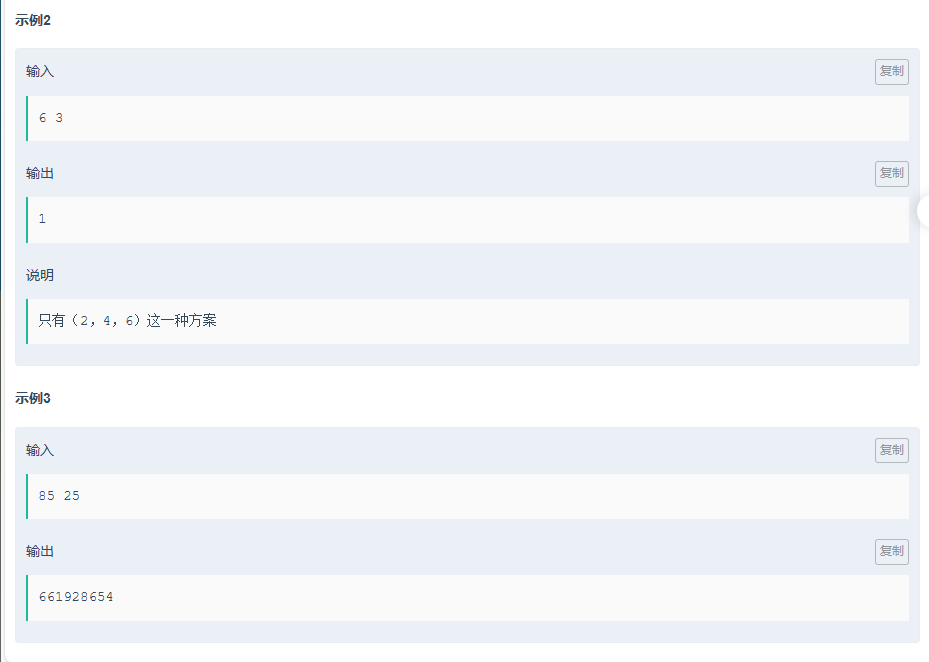
对于这一题，既然最大公因数为1的不满足，那就求出最大公因数大于等于2的。

一、问题转化：补集思想 + 容斥原理

题目要求 选 m 个石头，且它们的 gcd 不为 1 的方案数。直接计算较复杂，采用 补集思想 + 容斥原理 转化问题：
补集思想

总合法方案 = 所有 gcd 为 d（d≥2）的方案数之和。

但直接枚举 d 会重复计算（比如 gcd 为 6 的方案会被 d=2 和 d=3 重复统计），因此需要容斥：从大到小枚举 d，减去其倍数的贡献。
容斥原理

定义 f[d] 为选 m 个石头、且它们的 gcd 恰好为 d 的方案数。

但直接求 f[d] 困难，因此先定义 g[d] 为选 m 个石头、且它们的 gcd 是 d 的倍数（即所有选中的数都是 d 的倍数）的方案数。

则根据容斥关系： f [ d ] = g [ d ] − ∑ k > d , d ∣ k f [ k ] f[d] = g[d] - \sum_{k > d,\ d|k} f[k] f[d]=g[d]−k>d, d∣k∑f[k]

通过从大到小枚举 d，用 f[d] -= f[k] 的方式实现容斥。
二，预处理：求组合数

递推：s[i][j] = s[i-1][j-1] + s[i-1][j]（选第 i 个元素则从 i-1 选 j-1，不选则从 i-1 选 j）。

这样可以在 O(n^2) 时间内预处理出所有需要的组合数，避免重复计算。
三，核心流程
1. 计算 g[d]：选 m 个 d 的倍数的方案数

对于每个 d（从 1 到 n）：

统计 1~n 中是 d 的倍数的数的个数，记为 num = n / d（因为 d, 2d, 3d, ..., kd ≤n → k = n/d）。

若 num ≥ m，则从 num 个数中选 m 个的方案数为组合数 s[num][m]，即 g[d] = s[num][m]；否则 g[d] = 0（不够选 m 个）。

for(ll i=1;i<=n;i++)
	{
		ll num=n/i;
		if(num>=m)
		f[i]=s[num][m];
		else
		f[i]=0;
	}

2. 容斥修正：从大到小枚举 d

为了得到恰好 gcd 为 d 的方案数 f[d]，需要减去所有 d 的倍数 k=2d, 3d, ... 的 f[k]：

for(ll i=n;i>=2;i--) {
    for(ll j=2*i;j<=n;j+=i) {
        f[i] = (f[i] - f[j] + mod) % mod;
    }
    ans = (ans + f[i] + mod) % mod;
}

从大到小枚举：保证处理 d 时，其倍数 k>d 已经被处理过，这样减去的 f[k] 是 "恰好 gcd 为 k" 的方案数，避免重复计算。

(f[i] - f[j] + mod) % mod：防止负数，用 mod 调整。

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=5e3+10;
const ll mod=1e9+7;
ll s[N][N];
ll f[N];
void pre()//预处理组合数
{
	for(ll i=0;i<=N;i++)
	{
		s[i][0]=0;
		s[i][i]=1;
		for(ll j=0;j<i;j++)
		{
			s[i][j]=(s[i-1][j-1]+s[i-1][j]+mod)%mod;
		}
	}
}
void slove()
{
	ll n,m;
	cin>>n>>m;
	ll ans=0;
	for(ll i=1;i<=n;i++)
	{
		ll num=n/i;//1~n中i的倍数的个数
		if(num>=m)// 若数量足够选m个
		f[i]=s[num][m];
		else
		f[i]=0;
	}
	// 第二步：容斥原理计算f[d] = 选m个数且gcd恰好为d的方案数
    // 从大到小枚举d，确保处理d时其倍数已被处理
	for(ll i=n;i>=2;i--)
	{
	// 减去所有i的倍数的f[j]（这些是gcd为j的方案，已被包含在g[i]中）
		for(ll j=2*i;j<=n;j+=i)
		{
			f[i]=(f[i]-f[j]+mod)%mod;
		}// 累加所有gcd≥2的方案数
		ans=(ans+f[i]+mod)%mod;
	}
	cout<<ans<<endl;
}
signed main()
{
	IOS;
	ll t=1;
	pre();
	// cin>>t;
	while(t--)
	slove();
	return 0;
}

I.猜数游戏(easy)

题目传送门：猜数游戏(easy)

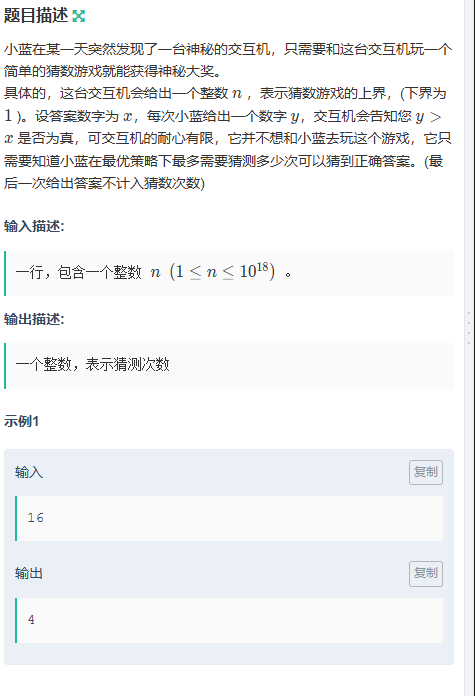
签到题没啥说的

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll ans=0;
void solve()
{
	ll n;
    cin>>n;
    ll sum=1;
   while(sum<=n)
   {
       sum*=2;
       ans++;
   }
    if(sum/2==n)
    cout<<ans-1<<endl;
    else
        cout<<ans<<endl;
}
signed main()
{
	IOS;
	ll t=1;
	//cin>>t;
	while(t--)
	solve();
	return 0;
	}

K.打瓦

题目传送门：打瓦

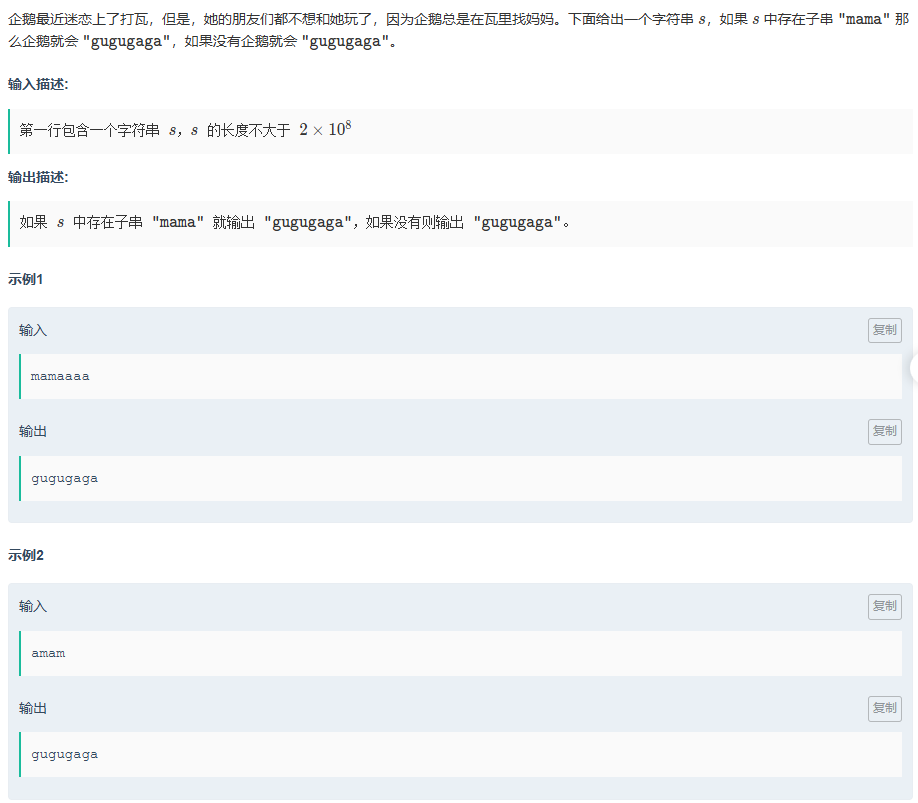
同样签到题

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
void solve()
{
	string s;
    cin>>s;
    cout<<"gugugaga"<<endl;
}
signed main()
{
	IOS;
	ll t=1;
	//cin>>t;
	while(t--)
	solve();
	return 0;
	}

M.米娅逃离断头台

题目传送门：米娅逃离断头台

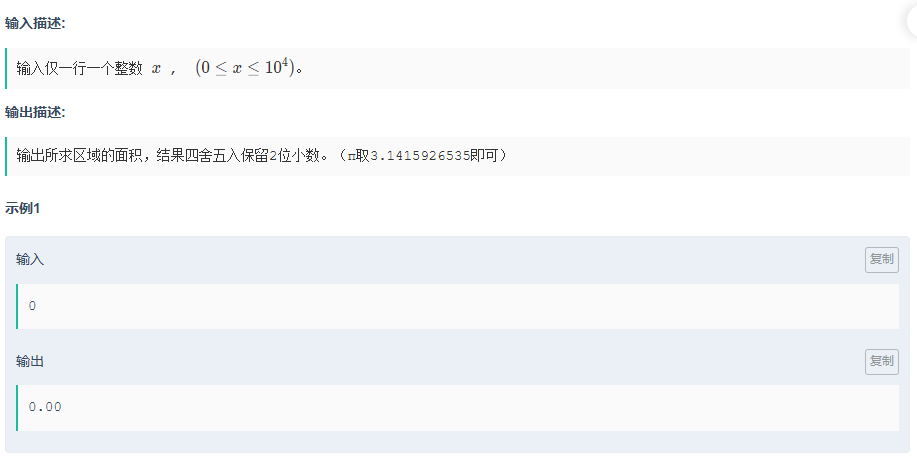
简单的数学题

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
double x;
void solve()
{
	cin>>x;
    double sum=3.1415926535;
    double ans=0;
    if(x==0)
    {
       printf("0.00\n");
        return ;
    }
    else{
        ans=(sum*x*x)/8;
        printf("%.2lf\n",ans);
    }
}
signed main()
{
	IOS;
	ll t=1;
	//cin>>t;
	while(t--)
	solve();
	return 0;
	}

总结

对于其他题，尤其a题就是属于没思路的一题

而D题，才开始题目没看太懂，没有建立无向边，建立的是有向边，等到后续给了题目更近一步的解释时，越来越迷糊，图论还是接触的少。