matlab矩阵的操作

一、复习线性代数

1.矩阵的定义

由m×n个元素组成的m行n列的数表（如下图）称为一个m×n阶矩阵，记为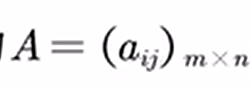

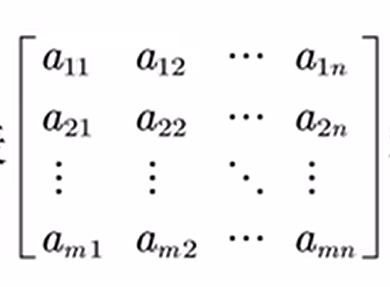
当m=n时，矩阵A为n阶方阵（或n阶矩阵）。

2.同型矩阵

两个矩阵行数和列数都相同。

3.转置矩阵

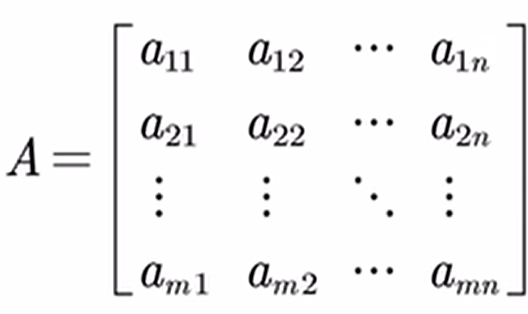
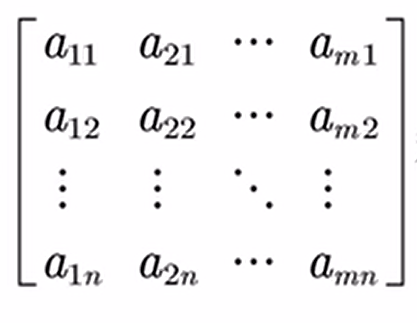是A的转置矩阵，记为

4.单位矩阵

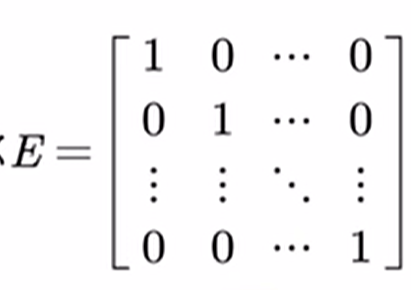
5.向量的定义

由n个数构成的数表[a,a2,...,an]或[a，a2,...,an]T称为n维行向量或n维列向量。显然，向量是矩阵的特例，行向量的行数为1，列向量的列数为1。

6.向量的模

设向量 α = [ a1 , a2 , a3 ]T，称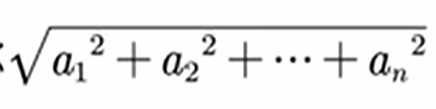为向量α的模，记为lal。

7.矩阵的加减法

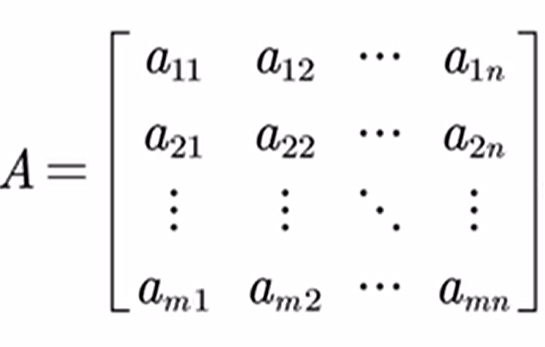
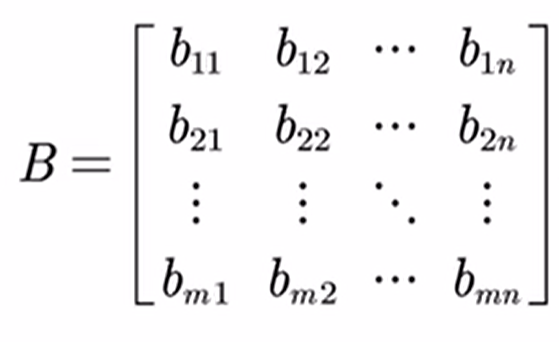
则A+-B=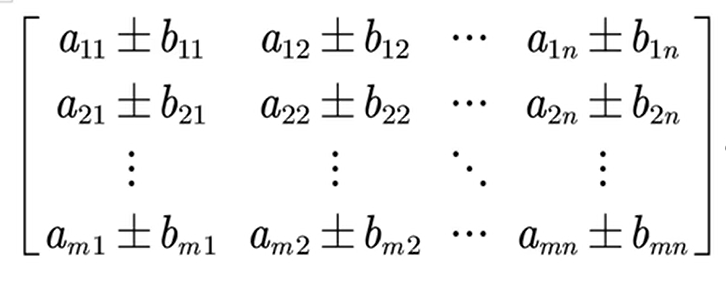

8.数与矩阵的乘法

9.矩阵与矩阵的乘法

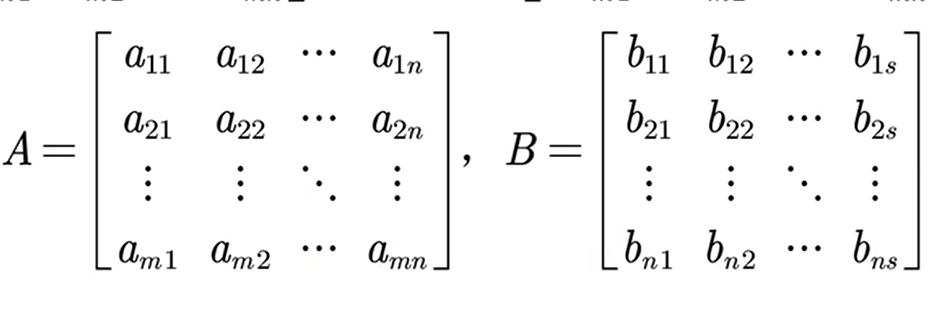
AB=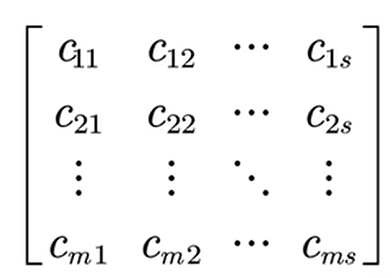，其中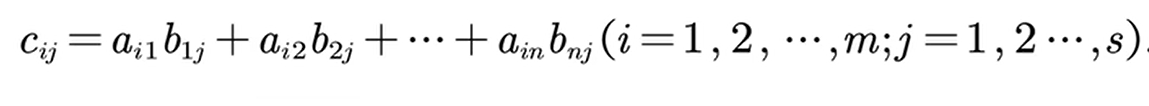

必须满足左边矩阵的列数与右边矩阵的行数相等。

10.矩阵的逆

设A是n阶矩阵，若存在n阶矩阵B，使得BA=E或AB=E，则称矩阵A可逆，矩阵B称为矩阵A的逆矩阵，记为B=A^(-1)。

11.特征值和特征向量

设n阶方阵A满足以下条件：存在数入（入可为复数）和非零n维列向量c，使得Ax=入x成立，则称数入是方阵A的特征值，称x为方阵A对应于特征值入的特征向量。注意，特征向量并不唯一，kx（k！=0）也是方阵A对应于特征值入的特征向量。

二、matlab中的向量

上一节我们知道，向量可以视为矩阵的一个特例：若一个矩阵的行数为1，则它可以视为一个行向量；若列数为1，则可以视为列向量；如果行数和列数同时为1，那么它就是一个标量（又称为常量、常数）。

学过其他编程语言的同学应该听过数组这个概念，在程序设计中，为了处理方便，我们需要把具有相同类型的若干元素按有序的形式组织起来，这些有序排列的同类型数据元素的集合就被称为数组。

在MATLAB的官方文档中，有时候也会出现数组这个概念。在MATLAB里，向量可以被称为一维数组，而我们常见到的由多行多列构成的矩阵可以被称为二维数组，这两个维度由矩阵的行和列表示。在MATLAB中，一维数组可以视为二维数组的一个特例。另外，在MATLAB中，我们还可以定义多维数组，多维数组是指具有两个以上维度的数组，绝大多数情况下我们不会用到，有兴趣的同学可以查看官方帮助文档。

以后在不引起误会的情况下，我们将MATLAB中的矩阵和数组视为同一个概念。

1.向量的创建方法

①直接输入法

a=[1,3,5]
b=[1 3 5]
c=[1
   3
   5]
d=[1;3;5]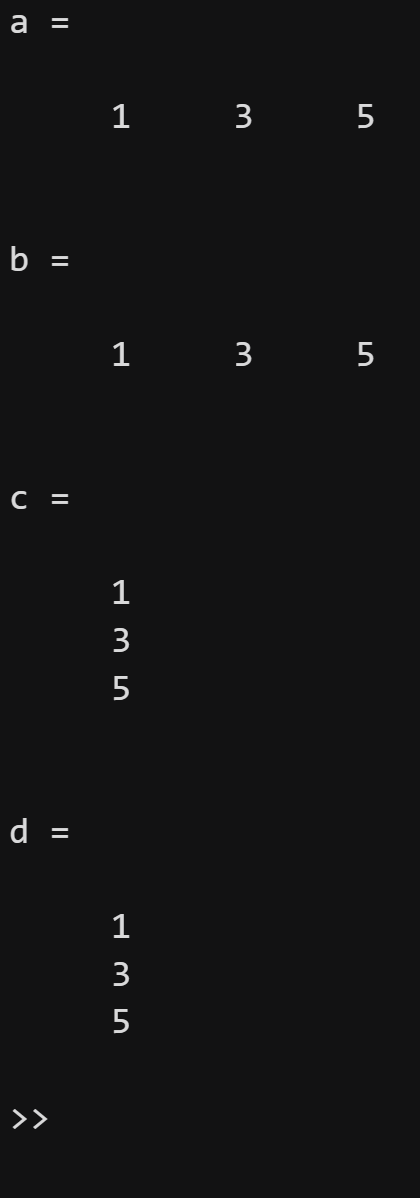

②冒号法：最常用

我们可以利用命令：A：step:B来创建一个行向量。

其中，A是起始值，Istep是每次递增或递减的步长，B是终止值（不一定刚好停在这里）。

若step等于1，则可以直接简写成A:B。

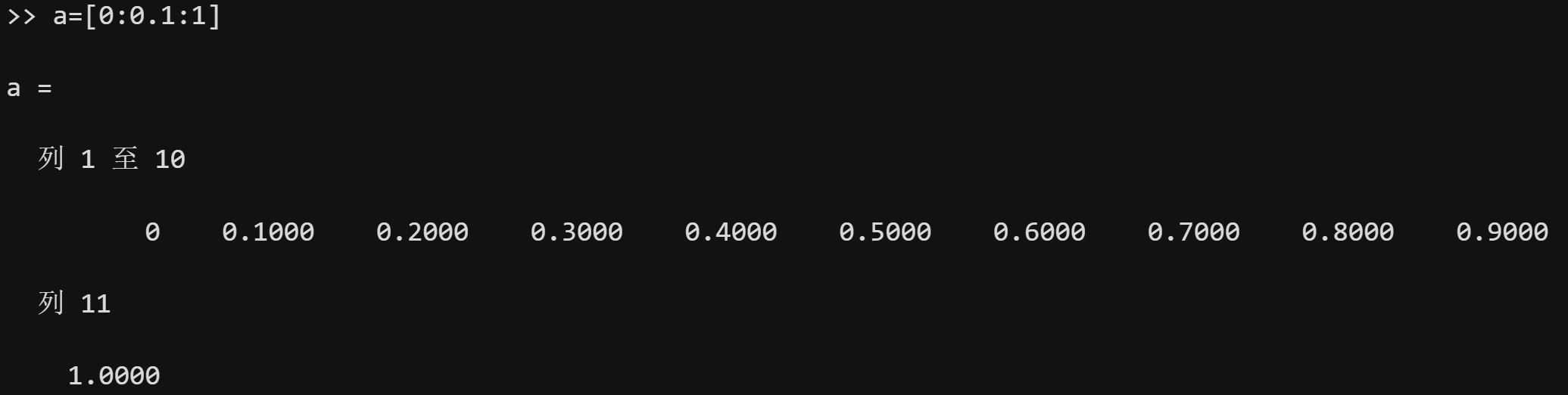
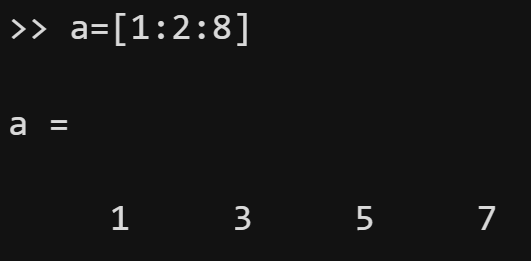
大家根据上面的例子应该很容易发现规律。下面再给大家补充两个知识点：

第一：上表中，有三种情况都会导致MATLAB返回空的向量：空的1xOdouble行向量。

怎么理解这个返回结果呢？这个"1×0"指的是向量的维度，你可以理解为1行0列，即这个向量是空的，不存在元素。在MATLAB中，我们可以直接使用命令[]创建空的向量。

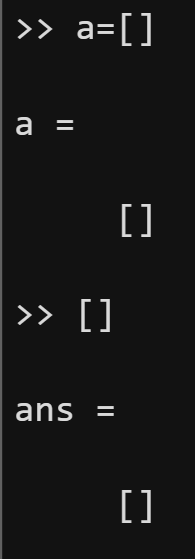
第二：MATLAB返回空的向量时，出现了一个英文单词：double。这里的double表示双精度浮点型，我在这门课中并没有特意去介绍数值的类型，原因是这一块的知识比较底层，涉及到数值在计算机中的存储方式。同时，和C、C++、JAVA等语言相比，MATLAB是偏应用的一门语言，其对数值类型的要求较弱。对数值类型感兴趣的同学可以先在b站学习C语言的公开课，然后再从MATLAB官网搜索数值类型的帮助文档进行学习。

③利用matlab函数创建

我们主要介绍两个函数：linspace和logspace，它们分别用来创建等差数列和等比数列。

首先介绍linspace函数，它有两种用法，区别在于是否给定第三个输入参数n，如果我们不指定n，则MATLlAB会默认n=100。这个函数使用的频率也很高，大家需要掌握。

●linspace(a，b)：该命令用来创建一个行向量，向量中的第一个元素为a，最后一个元素为b，形成总数为100个元素的线性间隔的向量。

●linspace(a，b，n)：该命令用来创建一个行向量，向量中的第一个元素为a ，最后一个元素为b ，形成总数为n个元素的线性间隔的向量。

初学者可能搞不懂linspace(a,b,n)和冒号法a:step:b生成向量的区别，我这里为大家总结：

（1）linspace不需要指定步长，MATLAB会根据你给定的元素个数n自动计算出来；而使用冒号法可以自己指定步长。

(2）linspace生成的向量的最后一个元素一定是b ，而使用冒号法A:step:B生成的向量的最后元素不一定是b。

（3）后续章节讲解循环语句时，冒号法使用的频率最高；而在绘制函数图形时，使用linspace得到的x轴的范围要比冒号法稍微准确一点。例如：我们要绘制sin(x)在区间[0，2π]上的图形，x的范围是0到2π，我们使用 linspace(0,2*pi)生成的向量的最后一个元素一定是2π；如果使用冒号法令x=0:0.1:2*pi，那么x向量的最后一个元素和2π有一个微小的差异，当然，如果我们将step取得更小，例如取成0.01，那么这个差异几乎可以忽略。

另一个函数是logspace函数它使用的频率不高，大家了解即可。它有两种常见的用法：

●logspace(a,b)：创建一个行向量，其第一个元素为10°，最后一个元素为10°，形成总数为50个元素的等比数列向量。

●logspace(a,b,n）：创建一个行向量，其第一个元素为10^a，最后一个元素为10^b，形成总数为n个元素的等比数列向量。

linspace 是 "Linear Space"（线性空间）的缩写。

2.向量元素的引用

对向量元素的引用（即提取向量指定位置的值）有两种情形，分别是提取向量中的单个元素和提取向量中的多个元素。在正式讲解之前，我们先来介绍索引（或下标）的概念。我们知道，向量分为行向量和列向量，它们在MATLAB中只有一个维度，因此我们可以利用向量中包含的元素个数来描述一个向量的大小。在MATLAB中，可以使用Iength 函数或numel函数来计算向量中包含的元素个数。

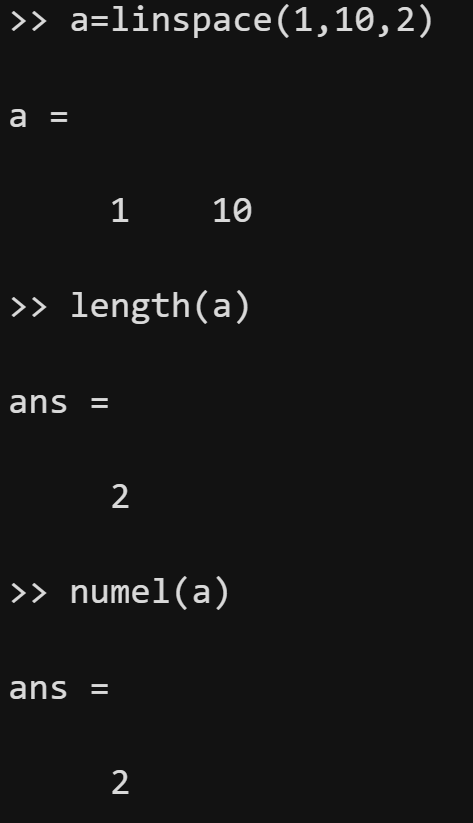
例如：a=[1,3,8,9,7];length(a)或numel(a)的返回结果是5，因为向量a中有五个元素。

假如我们有一个行向量a，里面包含了n个元素（n是大于等于1的常数)，它们分别是a1,a2,,am，那么我们可以列一个表格：

从上表可以看出，索引就是指某一个元素在向量中对应的位置，也可以称为元素在向量中所处的下标，在MATLAB中，向量的索引是从1开始的。

举个具体的例子，假设向量a=[2481632641282565121024]，那么a中有10个元素，因此a的最大索引是10。

（1）单个元素引用

我们提取向量a中单个元素的方法很简单，只需要利用a(ind)命令，小括号中的ind就是你要提取的对应元素的索引。（注意：创建向量用中括号，提取元素要用小括号哦！）

例如：a（1)的结果为2，因为a中第1个位置（索引或下标等于1）的元素是2；类似的，a(9)等于512，因为a中第9个位置的元素是512。

有些同学可能会好奇，如果我取索引为11，即输入a（11)会出现什么情况？

MATLAB会报错："索引超出数组元素的数目（10）"，即告诉我们，现在这个向量中元素的数目只有10个，即最大索引是10，而你取了索引11的元素，超出了取值范围。

如果a为空：

（2）多个元素引用

类似的，我们也可以利用向量的索引来同时提取多个位置的元素，这时候只需要将ind设

置成一个向量，ind中放入我们想要提取的元素的索引，然后使用a(ind)命令即可。

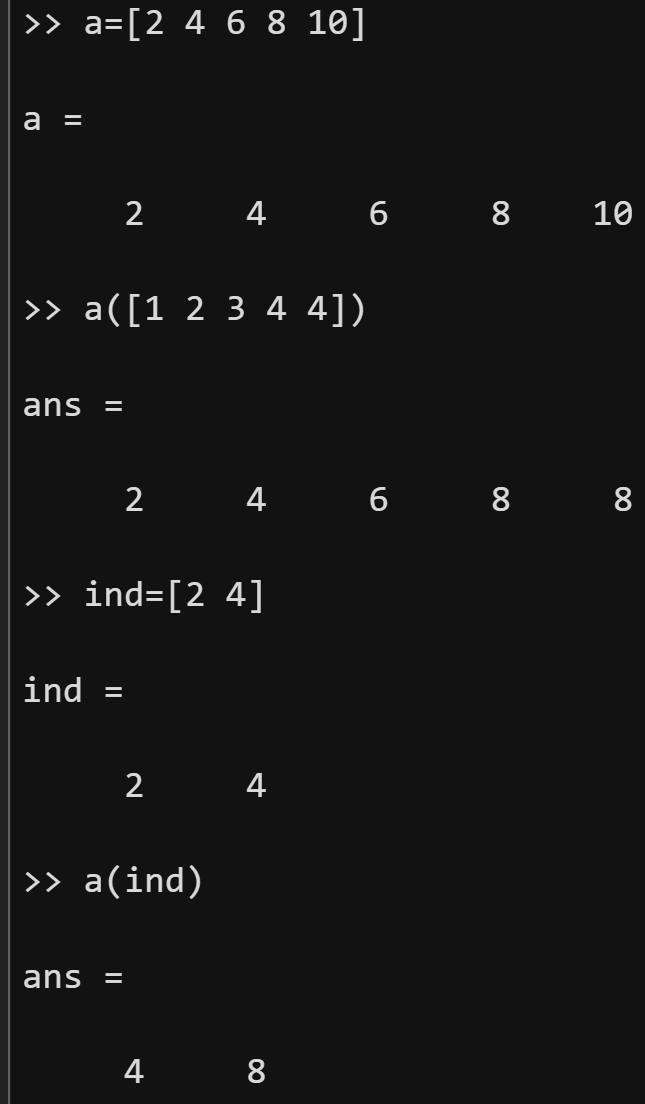
例如，我们令 ind=[13579]，那么a(ind)的结果为[2832128512]，即我们提取了向量a

中奇数位置的元素。熟悉向量冒号创建方法的同学应该能够看出，ind等于1:2:9，因此我们可

以直接将a(ind)写成a(1:2:9)，这就表示提取a中奇数位置的元素；类似的，提取a中偶数位置

元素的命令是a(2:2:10)，如果你不熟练的话，可以分成两步写，即先令ind=2:2:10，然后再使

用a(ind)的命令。当然，对于同一个位置的元素，我们也可以提取多次，例如：ind=[12233

3]，那么a(ind)得到的结果应该是[244888]，以后熟悉的话可以直接写成a([122333])。

技巧：使用end索引

有同学会想，假如我不知道向量a中有多少个元素，也不想使用length函数或者numel函

数来计算向量中元素的个数，那我能不能提取出a中奇数位置的元素呢？这时候就需要用到一

个特殊的关键字：end。它有很多种用法，在这里end可以用来替代向量的最后一个索引。

例如，我现在要访问a中第五个至最后一个元素，那么我们可以直接使用a（5:end)，这里的end就表示了a的最后一个索引；另外，我们还可以对end进行计算，例如要访问a中第五个至倒数第三个元素，我们可以使用a(5:end-2)，得到的结果为[3264128256]。这里有一个易错点，如果使用了end，不能将要取元素的索引赋值给ind。例如，还是要访问a中第五个至最后一个元素，如果你令ind=5:end，MATLAB就会报错。因此，我们只能在a后面的小括号中使用end来替代数组的最后一个索引。那我们回到上面的问题，在不知道a中有多少个元素的前提下，我们可以使用a（1:2:end)最后请大家思考：如何将一个向量倒序？例如原来的向量是[1 5 8 4]，倒序后是[4 8 5 1]。

3.向量元素的修改和删除

如果右边为常数，则将指定位置的元素全部变成这个常数。

如果我们将等号右侧变成空向量[ ]，则表示删除对应位置的元素。

三、matlab中的矩阵

（1）直接输入法

我们先来看直接输入法，直接输入法适用于矩阵中元素数量较少的情况。

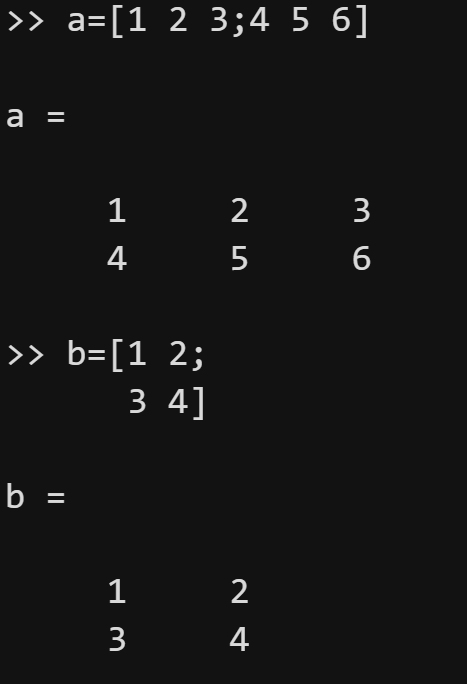
输入矩阵时要以中括号"[]"作为标识符号，矩阵的所有元素必须都在中括号内。矩阵的同行元素之间用空格或逗号分隔，行与行之间用分号或回车键分隔。

例如：命令a=[123;456]；可以在工作区创建出变量名为a的矩阵

（2）函数创建法

MATLAB提供了一些函数，这些函数可以用来生成某些特定的矩阵，我们这里介绍几组最常用到的函数。

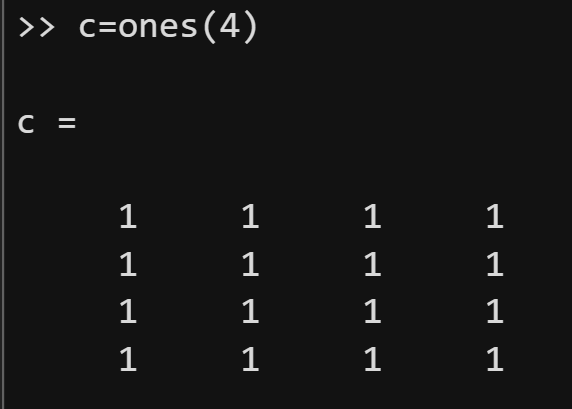
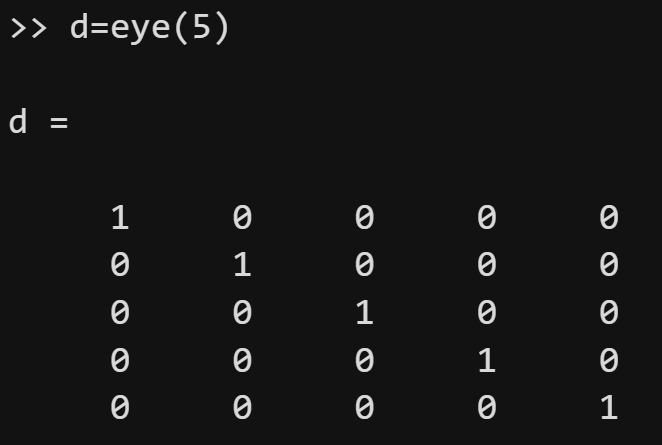
第一组函数：zeros、ones 和 eye。

这三个函数分别用来创建全为0的矩阵、全为1的矩阵和单位矩阵

eye 这个名字是一个非常巧妙的双关语：它既描述了矩阵对角线元素排列像一只眼睛 ，又谐音了代表"恒等元素"的字母 I。

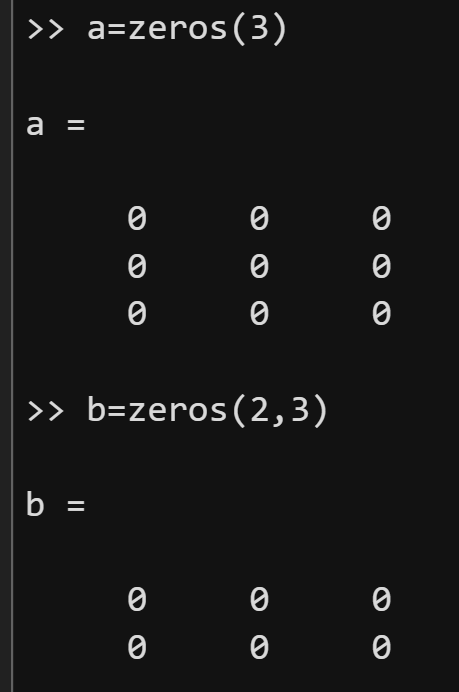
以zeros函数为例，其常见的用法有两种：

（1)zeros(n)可以创建一个n行n列全为0的矩阵；

（2）zeros(m,n)可以创建一个m行n列全为0的矩阵。

第二组函数：rand、randi和randn。

这三个函数分别用来创建均匀分布的随机数、均匀分布的随机整数和标准正态分布的随机数，以后会大量用到，请大家熟记。（数据的分布是概率论里面的知识点，没学过的同学可以搜索关键词自学）

i：int

n：normal

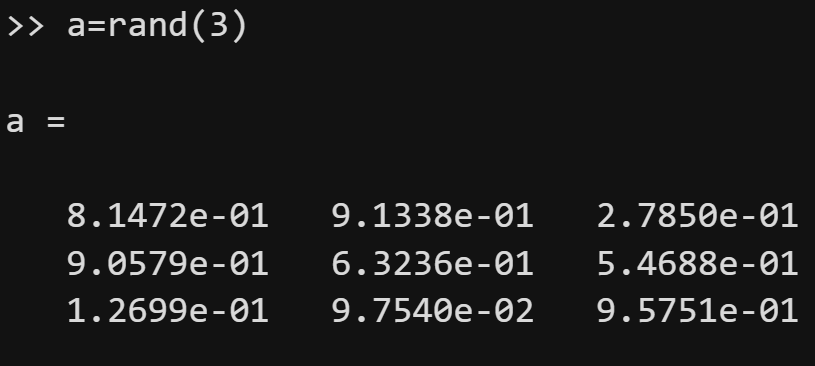
rand函数用来创建区间0和1内均匀分布的随机数，其最常用的方法有两种：

（1)rand(n）可以创建一个n行n列的随机数矩阵；

（2）rand(m，n)可以创建一个m行n列的随机数矩阵。

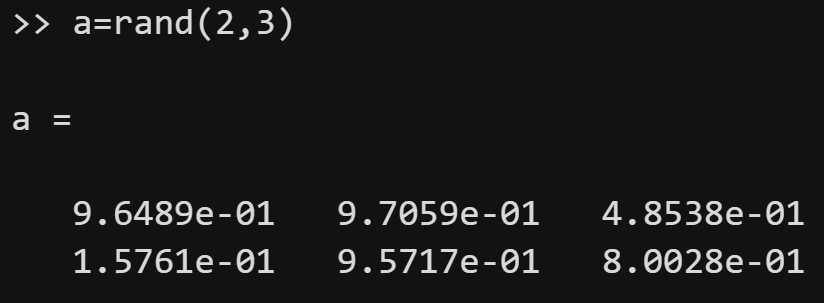
由rand函数创建的随机数矩阵的每个元素都随机取样自0和1之间的均匀分布。

randi函数用来创建均匀分布的随机整数，其最一般的用法为：randi([imin，imax]，m,n)，该命令可创建一个m行n列的随机数矩阵，随机数矩阵中的每个元素都是从区间[imin，imax]内随机抽取的整数。举个例子，假设我们要模拟投掷100次骰子，骰子有6个面，那么我们可以使用randi([1，6]，1,100)得到一个长度为100的行向量，向量中的每个元素都是取自1，2，3，4，5，6。

如果m和n相同，即生成一个n行n列的方阵，那么可以直接写成randi([imin,imax],n)。

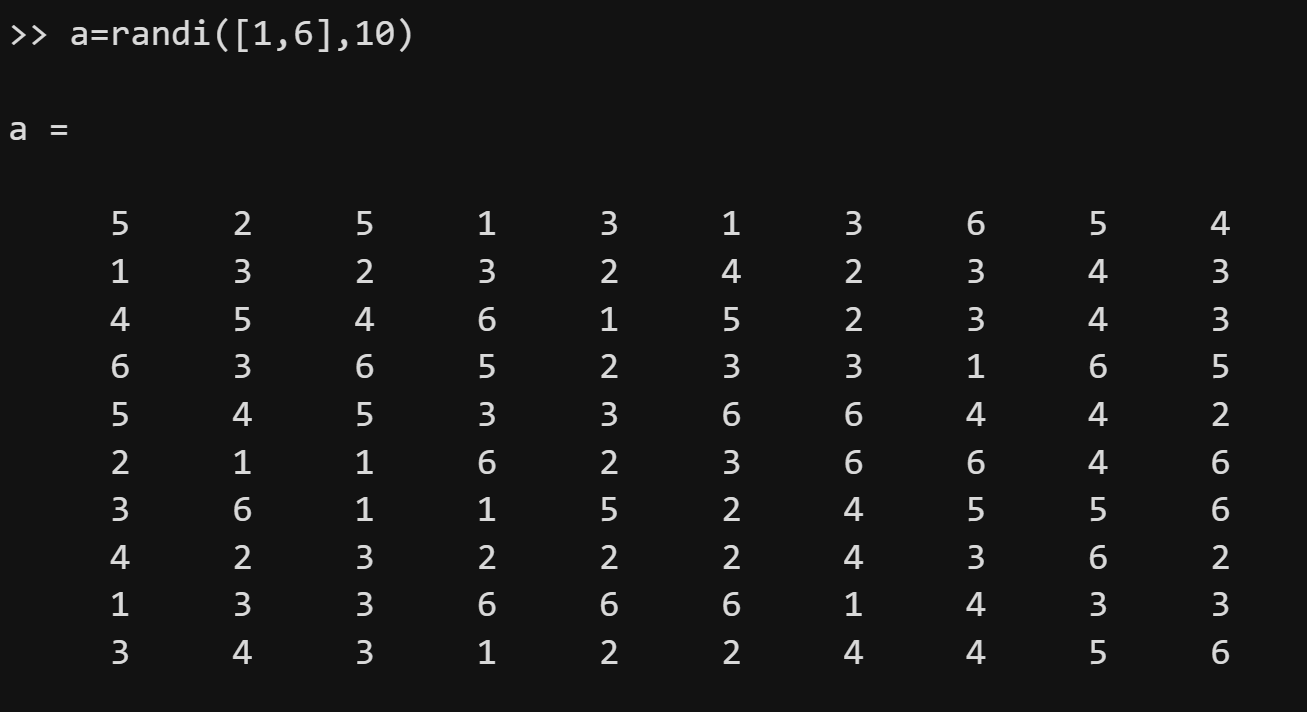
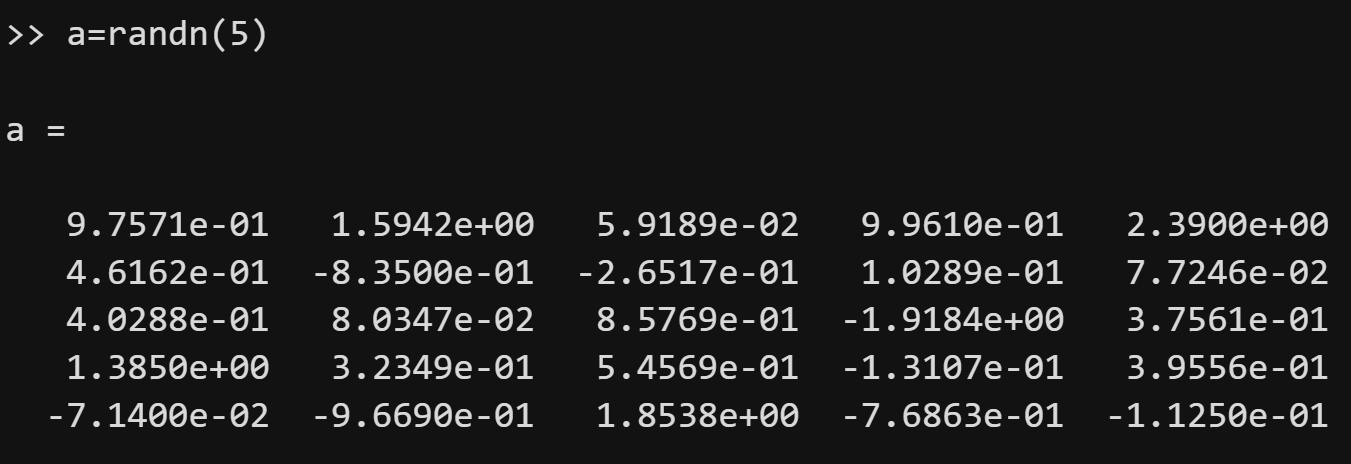
randn函数用来创建标准正态分布的随机数，其使用方法和rand函数类似：

(1）randn(n)可以创建一个n行n列的随机数矩阵；

(2）randn(m,n)可以创建一个m行n列的随机数矩阵。

由randn函数创建的随机数矩阵的每个元素都随机取样自标准正态分布。

标准正态分布：以0为平均数、以1为标准差的正态分布，记为N（0，1）。

第三组函数：diag 和 blkdiag。

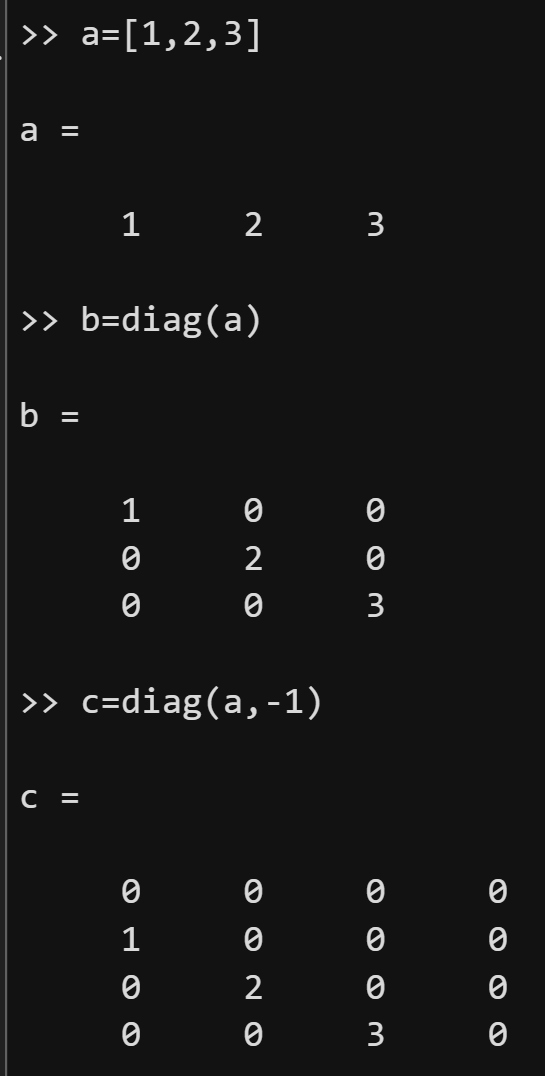
diag函数可用来创建对角矩阵或者获取矩阵的对角元素

情况1：如果输入的第一个参数是向量，则表示创建对角矩阵。diag(v,k)将向量v的元素放置在第k条对角线上，其他位置元素为0。k=0表示主对角线，k>0位于主对角线上方，k<0位于主对角线下方。如果k=0，可以直接写成diag(v)。

diag 是英文单词 Diagonal（对角线）的缩写

blk：block 分块

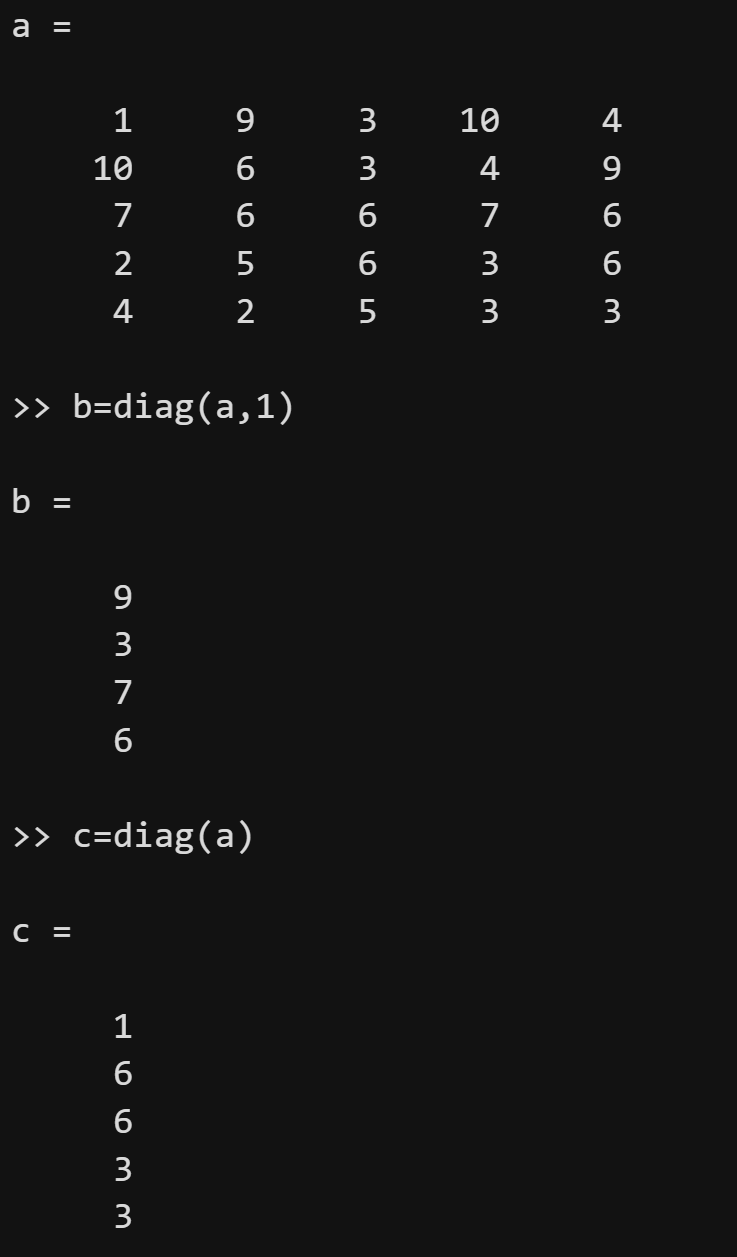
情况2：如果输入的第一个参数是矩阵，则表示获取矩阵的对角元素。diag(A，k)返回A的第k条对角线上元素的构成的列向量。

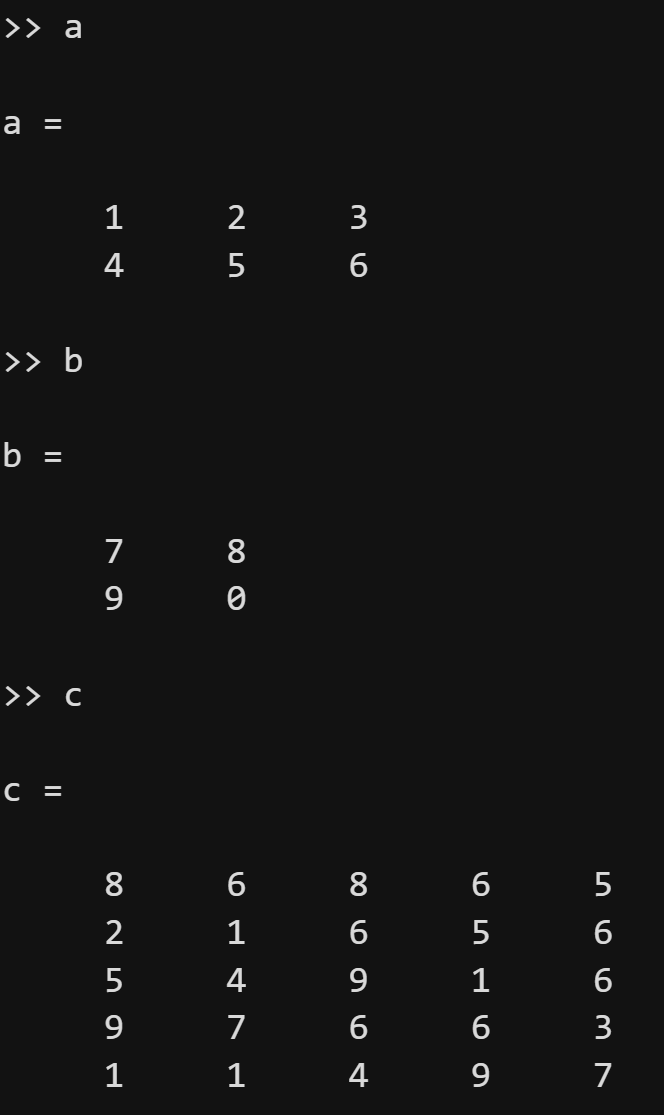
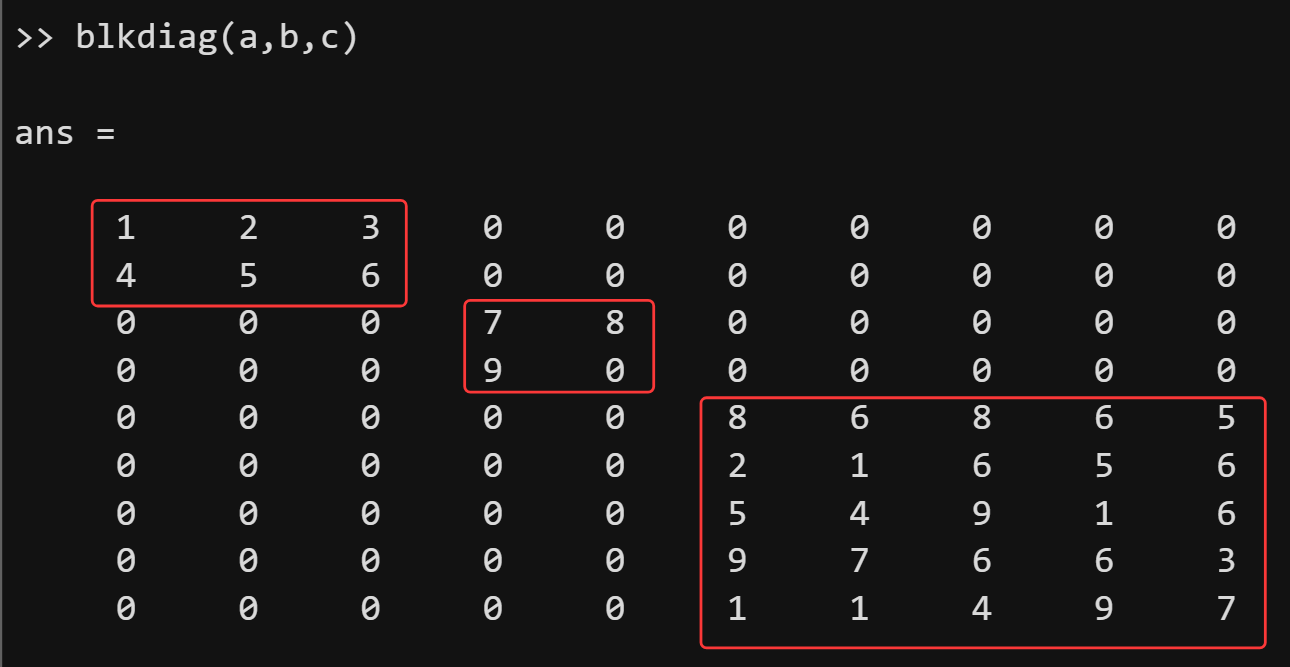
blkdiag函数可用来创建分块对角矩阵。

分块对角矩阵是相对于常规的对角矩阵而言的，常规的对角矩阵沿对角线具有单个元素，而分块对角矩阵的对角线的元素是矩阵。我们可采用以下形式表示一个分块对角矩阵：

（3）导入本地文件中的数据

MATLAB可读取本地的文件，支持的常见格式如下：

>.txt、.dat或.csv（适用于带分隔符的文本文件）

>.xls、.xlsb、.xlsm、.xlsx、.xltm、.xltx或.ods（适用于电子表格文件)

由于这一块的内容比较丰富且可能涉及我们没学过的知识点，所以会放在后面的章节进行讲解。到时候我们会重点学习MATLAB菜单栏："主页------导入数据"这个功能。

（4）矩阵元素的引用

上方给出了一个m行n列的矩阵，对于第i行第j列的元素，我们用aj表示。因此，我们可以使用矩阵元素所处的行(row)和列(column)来进行引用矩阵的某一个元素，方式为:a(row_ind,column_ind).这里的row_ind表示要引用的元素的行索引，column_ind表示列索引。如果row_ind和column_ind都是一个常数，则表示提取矩阵中的单个元素；如果row_ind或column_ind是包含有多个元素的向量，则表示同时提取多个位置的元素。与向量类似，end也可以用来替代最后一个索引，通常和冒号法一起使用。

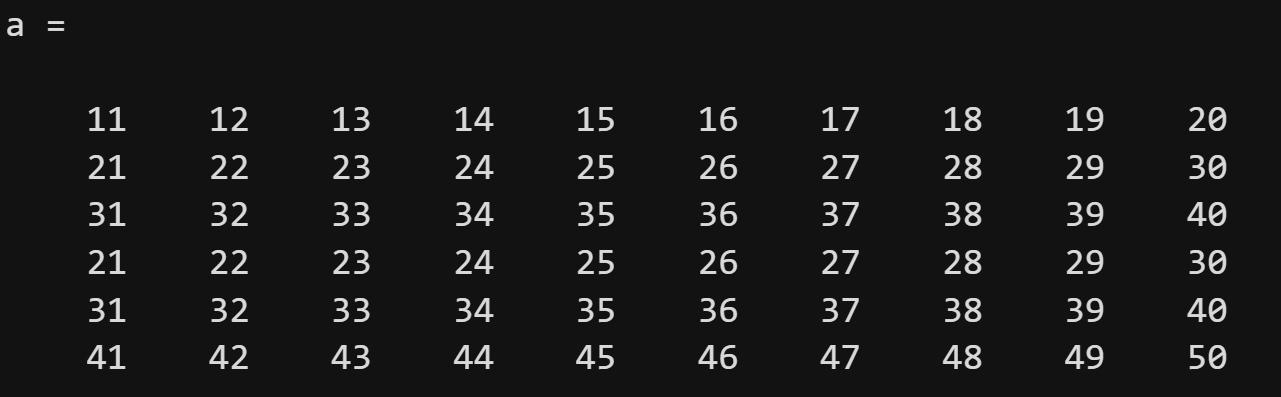
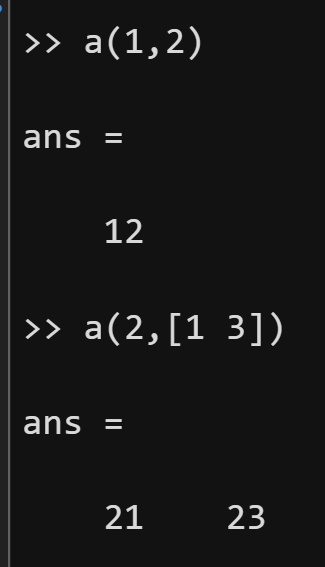
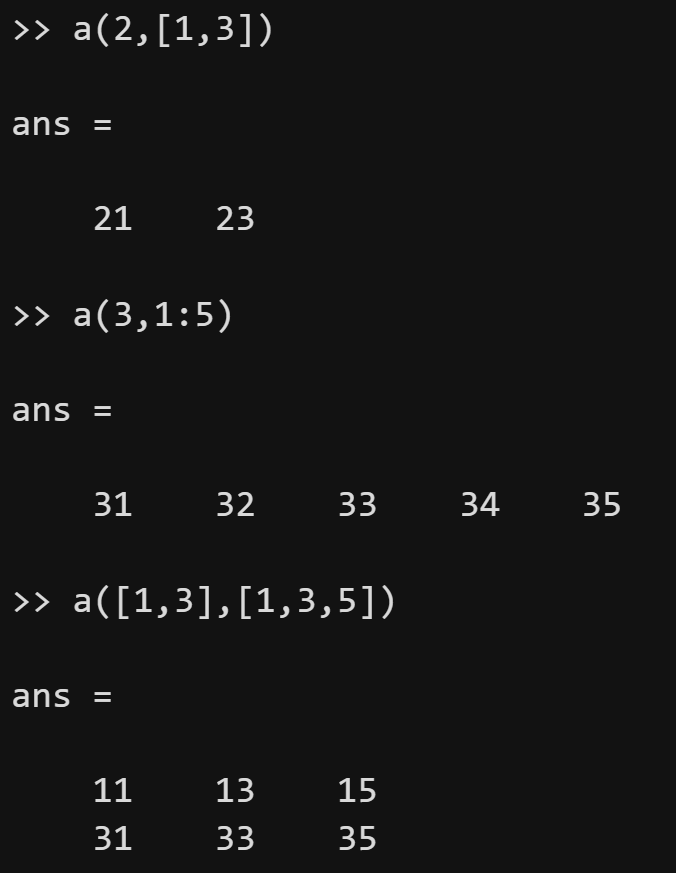
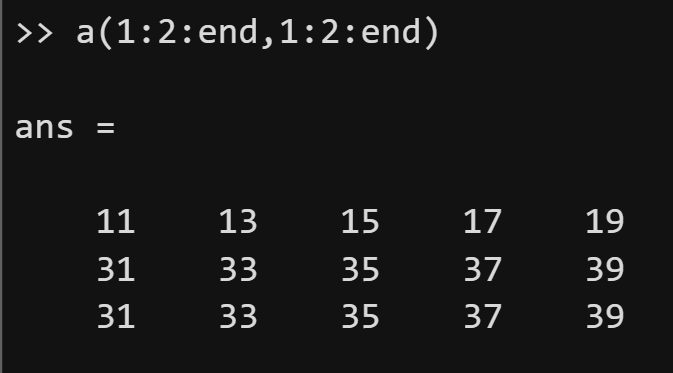
前面我们学过，可以使用length函数和numel函数来计算向量中包含的元素个数。那么，怎样计算一个矩阵的大小呢？我们可以使用size函数，它有两种常见的用法：

(1）size(A)返回一个行向量，其元素是A的各维度的长度。若A是一个3X4的矩阵，则 size(A)返回向量[3 4]；如果让[r,c]=size(A)，那么r=3,c=4。

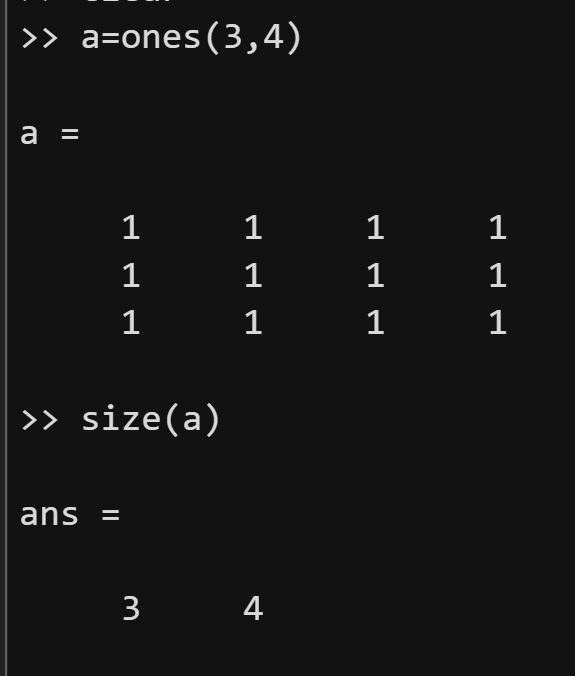
(2)size(A,dim)返回在维度dim上的长度。dim=1时表示行；dim=2时表示列。若A是一个3X4的矩阵，则size(A,1)返回3，size(A,2)返回4。

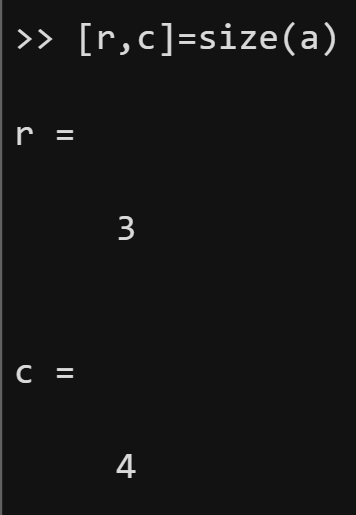
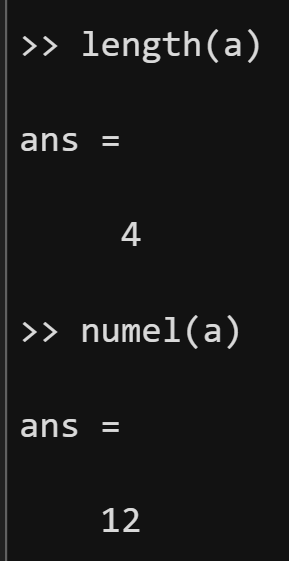
（(length函数和numel函数也可以用在矩阵上。length函数会返回行和列的较大值：对上面的A矩阵，length(A)返回4；numel函数会返回矩阵中元素的总数，numel(A)返回12)

有时候我们需要取出矩阵的某一行或者某一列。以取出矩阵A的第一行为例，我们可以使用代码A(1，1:end)，row_ind取1表示第一行，column_ind取1:end表示从1到最后一列的索引。这时候我们可以直接将其简写为：A（1，），逗号后面是列索引的位置，加一个冒号就表示取出每一列的元素。同理，要取第一列的所有元素，我们可以使用代码：A（：，1).