AI可以帮助我们找到问题的解决方案，比如：导航应用程序中帮我们规划从出发地到目的地的最佳路线、玩游戏时规划好下一步动作以提高胜率。
本节的搜索问题涉及到一个被赋予初始状态和目标状态的代理（Agent），该代理则需要返回一个从初始状态达到目标状态的解决方案。
例如导航就使用了典型的搜索过程，其中，代理（程序的思考部分）接收用户的当前位置（起点）和目的地作为输入，再根据搜索算法得出并返回一条推荐的路线。不过还有许多其他形式的搜索问题，例如拼图和迷宫。
我们以15拼图来举例，如图：
该游戏的规则是：在15块拼图打乱顺序的基础上，通过滑动拼图（上下左右）将这15块拼图按数字从小到大的顺序还原成上图所示。
要解出15拼图，就需要用到搜索算法。
在分析解决方案前，我们需要引入一些术语。
术语
代理（Agent）
我们首先需要考虑的是代理 （Agent）------ 是感知其环境的某个实体，它能够以某种方式感知周围的事物，并以某种方式对该环境采取行动。
例如：在导航中，我们的代理可能是汽车的一种表示形式，它会根据我们的当前位置、地图信息、路况等来帮助我们决定下一步走哪条路；游戏里的NPC敌人也是一种代理，它会不断观察玩家的位置，并决定是追击、躲避还是攻击。
而在上面15拼图的情况下，代理（Agent）可能是AI或试图解决这个谜题的人，通过观察来弄清楚要移动哪些图块才能找到该解决方案。
其感知的环境则称为状态 （State），接下来我们介绍状态的概念。
状态（State）
状态则是代理在某一时刻的环境配置。
例如：在15拼图中，状态是所有数字排列在棋盘上的任意一种方式。（下图则是棋盘可能存在的3种状态）
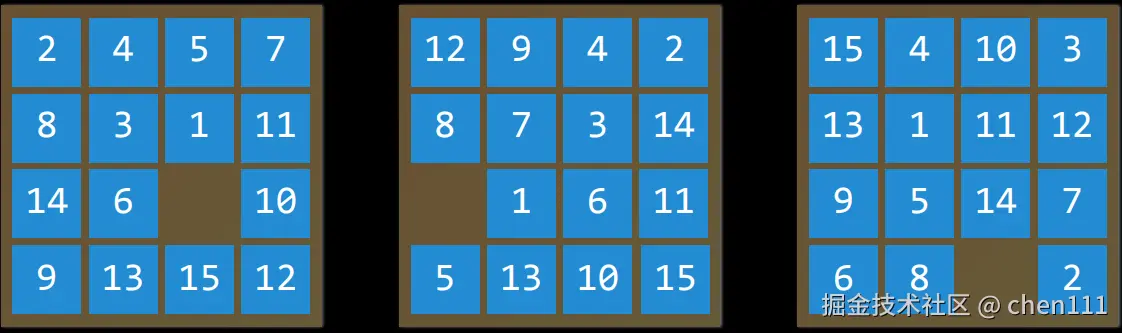初始状态 （Initial State）则是搜索算法开始的状态。例如在导航中，Initial State就表示当前位置（起点）。
我们将从这个初始状态开始，然后推理，思考我们可以采取哪些行动才能从初始状态到目标状态。我们如何从初始状态到达目标？归根结底，需要通过采取行动。
动作（Action）
Action是我们在任意给定状态下做出的选择。就上文中提到的15拼图而言，我们首先通过初始状态来决定一个拼图往一个方向移动，移动后就更新成另一种状态，然后再根据新的状态来决定下一次的动作。一直重复这个步骤，直到达到目标。所以这将是一个反复出现的步骤，我们不如将其更精确地定义为函数，以便反复使用。
因此，我们定义了一个名为 Actions 的函数 ------ Action(s)
其输入值 s 则表示目前所处的状态，而其返回值则是在该状态下可能执行的动作的集合。
例如，拿下图来说：
该图上15张拼图的顺序作为此刻的状态输入到Action函数中，输出为两个可能执行的动作，即：15号拼图向右移动、12号拼图向下移动。
当我们执行了动作后，又会得到一个新的状态，我们把这种新的状态称作状态转移模型（Transition Model）。
状态转移模型（Transition Model）
描述在任意状态下执行某个动作的结果。同理，也可以将状态转移模型定义成一个函数 ------ Result(s, a) ，以当前状态 s 和执行的动作 a 作为输入，以执行动作后呈现的新的状态作为输出。例如：
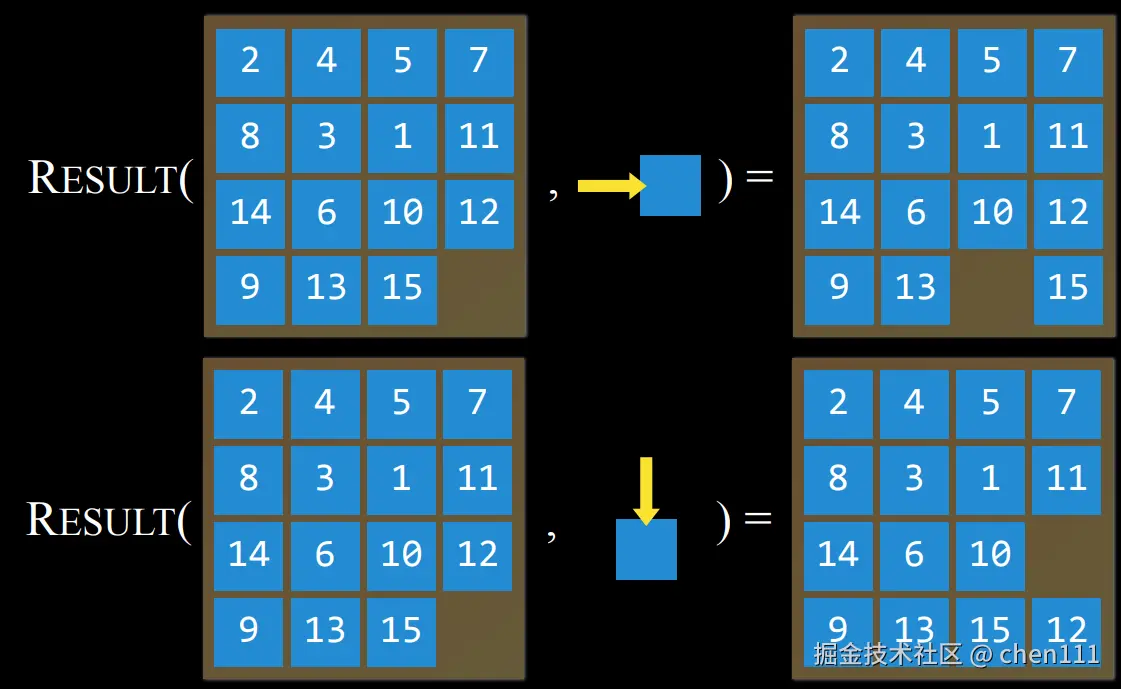状态转移模型描述了状态和动作是如何相互关联的。
而从初始状态出发，通过任意一系列动作得出的Result函数的返回值的集合，就称为状态空间（State Space）。
状态空间（State Space）
从初始状态出发，通过一系列动作能得出的所有状态的集合，就称作 State Space。 通常，为了简单起见，我们会以图的方式来展示整个事件 由于我们可以在前后两个动作之间相互切换，也就是我可以从第一步到第二步，又能从第二步回到第一步，所以，可以将State Space可视化为有向图，节点表示为不同的状态，每个节点间的双向箭头就表示为动作。
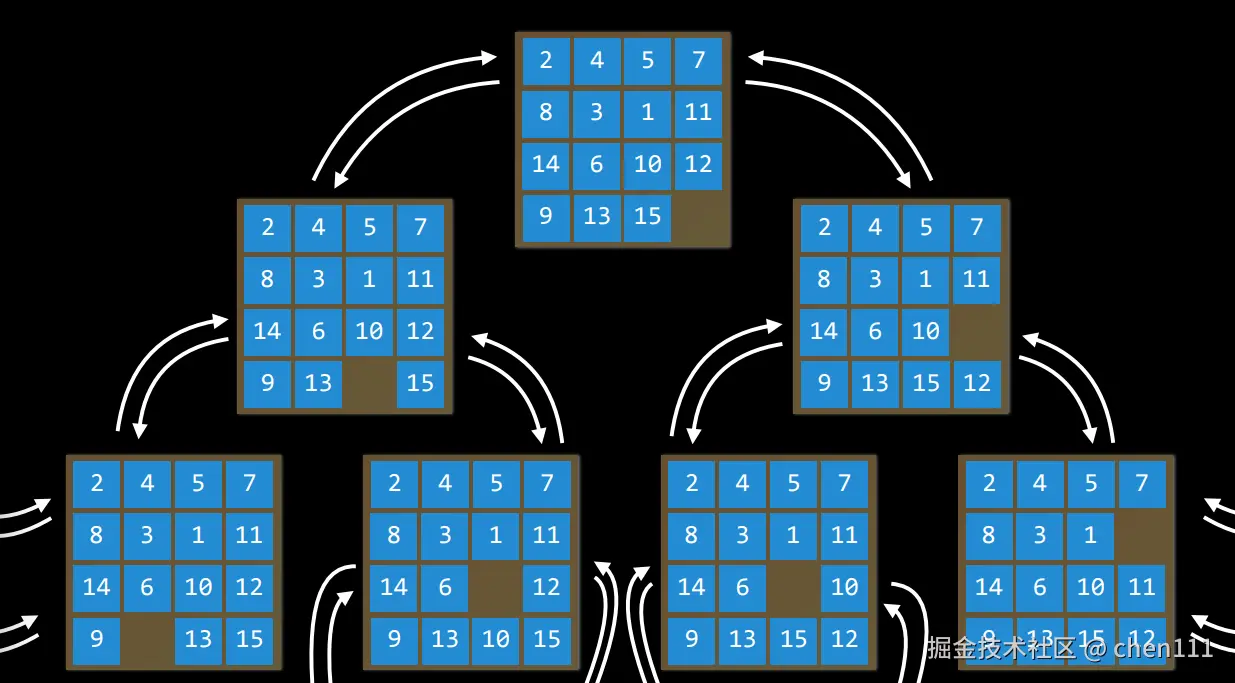这是部分State Space的有向图。
现在我们已经有了这些概念：
- 节点表示各种状态
- 动作可以让我们从一个状态转移到另一个状态
- 状态转移模型定义了我们执行某个特定的动作之后会发生什么。
这些都是在我们解决问题的过程中会涉及到的，但问题是，我们如何确定AI什么时候才解决完问题？
所以我们需要在AI中code出一个目标测试（Goal Test）。
目标测试（Goal Test）
Goal Test为判断给定状态（一般为当前状态）是否为目标状态的方法。例如，导航中的目标测试为判断你当前所处位置是否为你的目的地。
但往往从一个初始状态到目标状态，会有多种解决方法，例如导航里面去往同一个目的地可能有多条路径供选择，而我们往往会选择最短的那条路径，也就是往往会选择成本低的解决方法。成本低对应不同的问题会有不同的表现方式，例如路径短、用时短、步骤少等等，如何判断某个解决方法的成本低，就需要通过其 路径成本（Path Cost） 来对比判断。
路径代价（Path Cost）
Path Cost是与某条路径相关联的一个数值型的代价。它可能表示距离、时间、费用、能量消耗等。导航就往往会选路径代价最低（路程最近或用时最短）的那条路线。
所以人工智能往往不只是找到解决方案，还要找到能够最大限度地减少这种路径代价的方法。
在理想状态下，AI不仅要找到解决方案，还应找到最优解决方案。
解决方法
对于迷宫这种游戏，我们无法确定选择的方向是否能通往目的地，因此就需要不断尝试，当尝试的方向碰到死路，再回到上一个选择，选择另一个方向，为了能执行这些操作，我们往往会选择节点这样的数据结构，其中每个节点又包含了以下数据：
- 一个状态
- 从父节点到该节点所执行的动作(Action)
- 从初始状态到该状态的路径成本
由于该节点只用来保存信息，因此我们需要借助frontier来帮我们完成搜索，这里的frontier相当于一个盒子，里面可以放入未处理或预处理的节点。
下面是个例子：
需要找到从A到E的路径，我们可以用深度优先遍历（DFS）：
Frontier 则是用栈实现的，里面放置的则是当前节点的子节点以及预处理的节点，处理一个则从里面移出一个。
但是也可能会出现"bug"，如图：
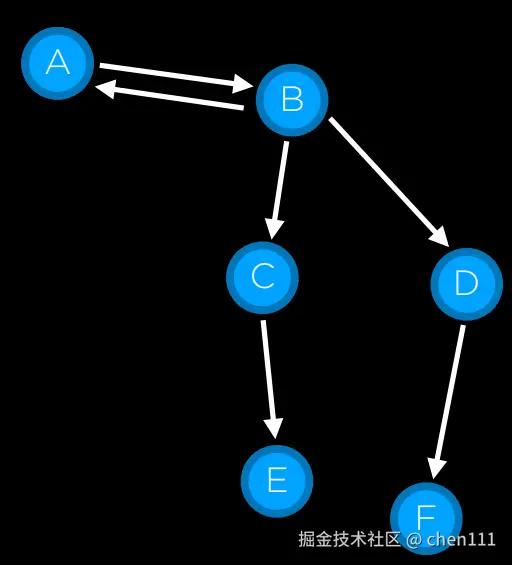A和B之间是相通的，若用上面那种方法则容易进入A和B交替的死循环，因此，我们再加入一个 explored set，里面用于放置已经遍历过的元素，现在，我们遍历的步骤就变成了这样：
遍历过程也就变成了这样：
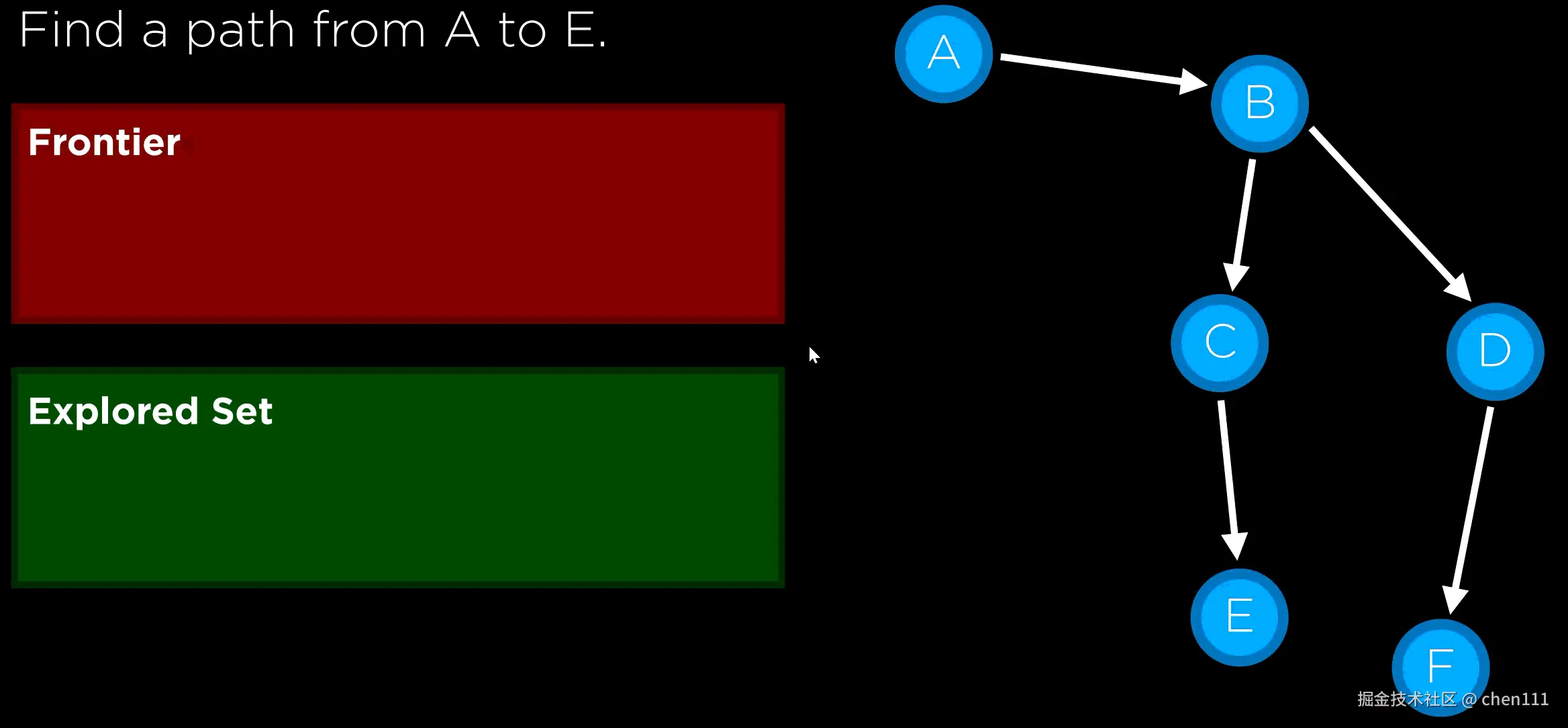
若要用广度优先遍历（BFS），则只需将Frontier 的结构改成队列（queue），过程如下：
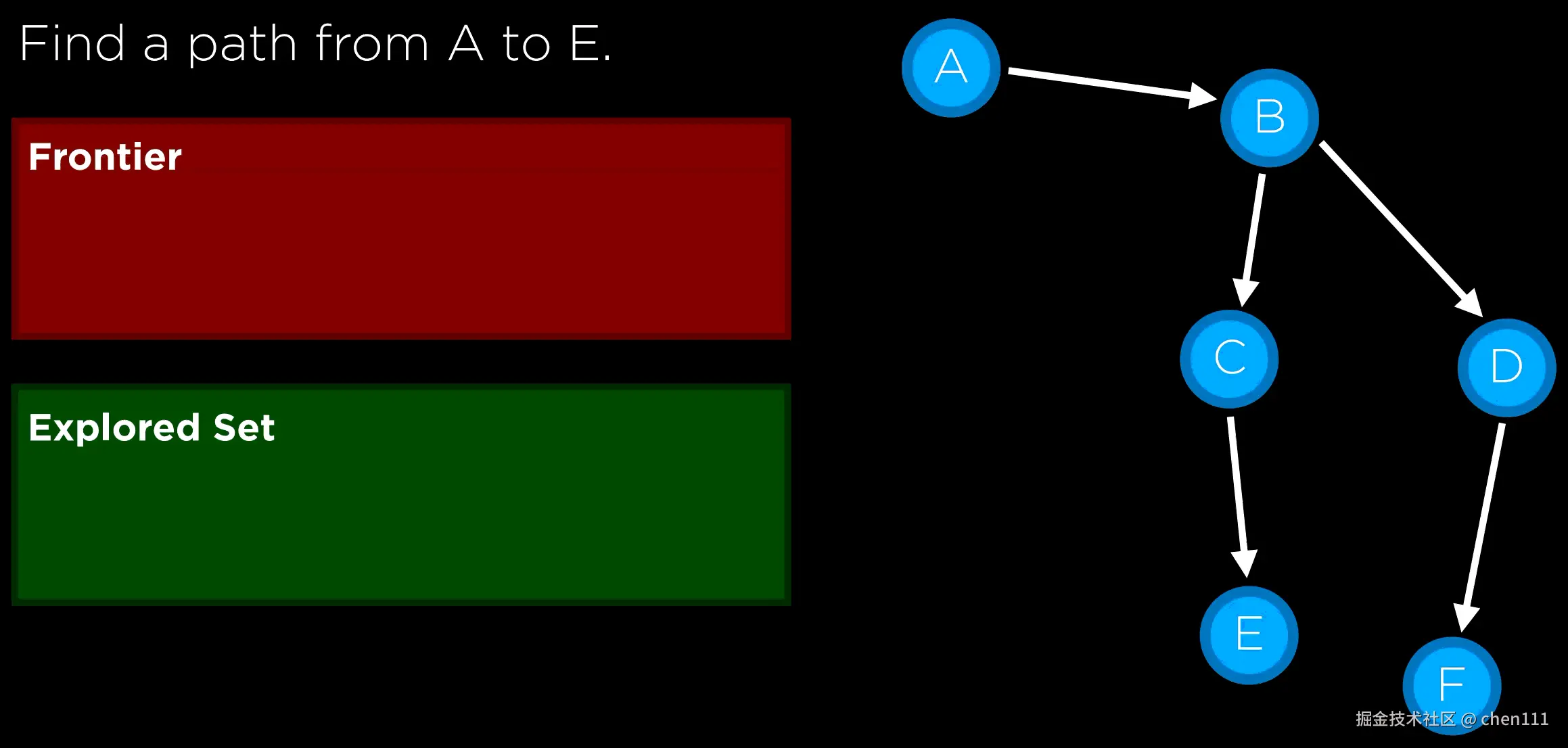好，现在我们已经大致了解如何实现DFS和BFS了，接下来转战迷宫问题。
迷宫
在我们小时候玩迷宫游戏时，对于那种复杂的迷宫，我们往往会选择一条路走到尽头，然后再回溯，这种方式也就是深度优先遍历。然而，虽然深度优先遍历在有限的迷宫地图中一定能找到通往终点的路径，但有时却不能找到通往终点的最优路径（最短路径），下图则是一种情况：
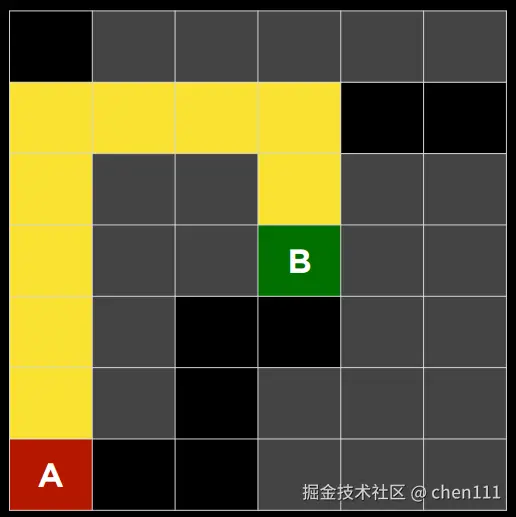很明显，从A点出发，先向右走才是最优路线，但往往DFS方法遇见岔路口先转哪个方向是随机定的。
如果用BFS呢？
若DFS是一条路走到尽头，那么可以理解BFS是"齐头并进"。下面是BFS的运行过程： 
显而易见，这种情况下的BFS能找到最优路线。 既然BFS一定能在有限的迷宫图中找到最优路径，为什么不全用BFS？
下面是一个迷宫图的两种解决效果：
DFS：
BFS：
由遍历的结果图可知，BFS遍历的状态比DFS更多。因此，在一定情况下，DFS会比BFS更节省内存。（保存的节点更少）
事实上，BFS和DFS都是无信息搜索算法（uninformed search），所谓"无信息"是指，这些算法在搜索过程中不会利用任何额外的、预先已知的问题信息，它们只依赖在探索过程中自己获取到的信息去决定下一步怎么走。也就是，不管处理的迷宫地图是什么样的，当遇见岔路口时处理的方法都是一样的。
但是，很多时候我们是可以获取一些关于问题的额外信息的，例如，当我们拿到迷宫地图，可以根据起点和终点的位置判断出应该向哪个方向移动，当我们走到岔路口时，可以看出哪一条路大致朝着出口方向，哪一条路"背道而驰"。
人工智能也可以利用类似思路------根据特殊情况进行针对性搜索。
因此，能利用这些额外知识、试图提升搜索效率的算法，叫做有信息搜索算法 （informed search algorithm）。 贪心最佳优先搜索 （Greedy Best-First Search）就是一种有信息搜索算法。
贪心最佳优先搜索（Greedy Best-First Search，GBFS）
贪心最佳优先搜索（Greedy Best-First Search）就是每次都挑看起来离目标最近的节点 去扩展，这个"最近"是靠一个启发式函数 h(n) 来判断的。
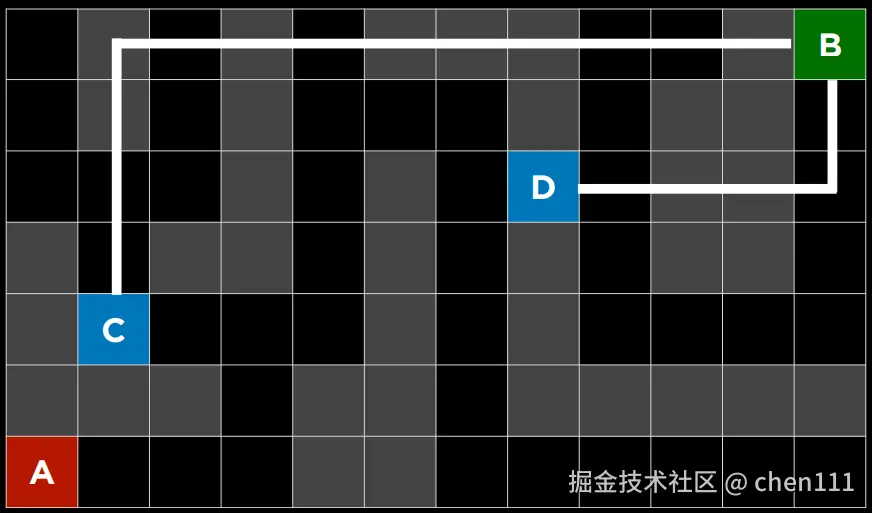
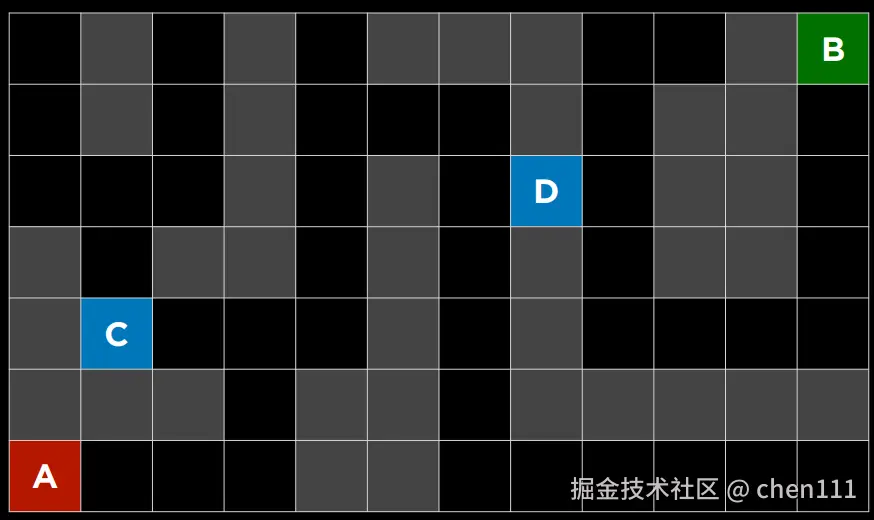如图，A是起点，B是出口，我在地图中选两个点C和D，让你选一个作为新的起点，在以到达终点B为目的的情况下，你会选哪个？
毋庸置疑，任何人看到都会选D。是因为我们忽略了墙的存在，即每格都是通的，这样，我们就可以将这个图看作一个二维坐标图，在知道A、B、C、D四个点的坐标的情况下，计算得D离B的距离更近。
这就是一种常见的距离计算的方法 ------ 曼哈顿距离（Manhattan Distance） （在二维平面上，两个点之间的曼哈顿距离 是它们在 x 方向的距离 + y 方向的距离）
在这里的启发式函数h(c)就是两点间曼哈顿距离的比较计算。
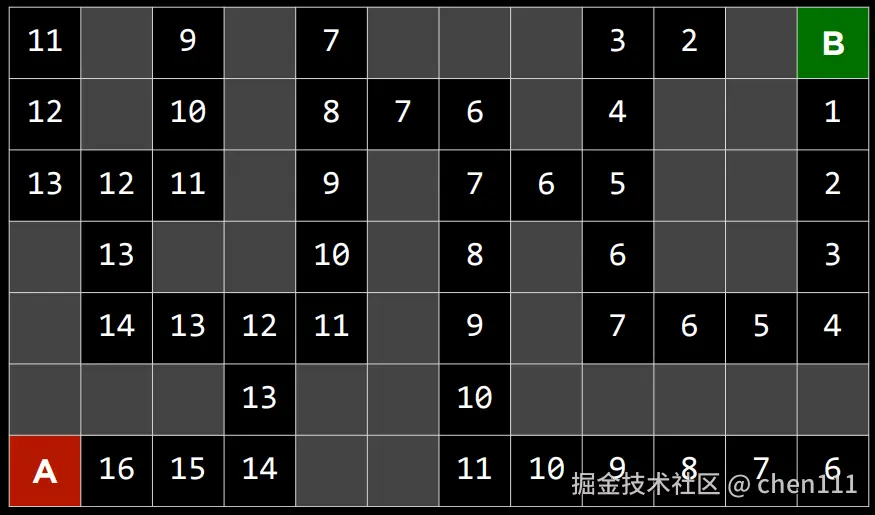这样，我们就能标出每个点对于出口的曼哈顿距离，并尽量走数值小的点。过程如下：
贪婪最佳优先搜索算法好不好用，效率高不高，很大程度上取决于这个启发式函数准不准。比如，在迷宫里，我们可以用"曼哈顿距离"来当这个估算方法：它完全不管墙壁，只计算从当前格子到目标格子上下左右走几步能到。但计算结果一定对吗？我们的计算是基于没有墙壁的，加上墙壁，实际情况也可能变化，所以:
这个函数是用来估算某个节点到目标还有多近，但说到底它只是估算，可能会出错。
下面就是一个例子：
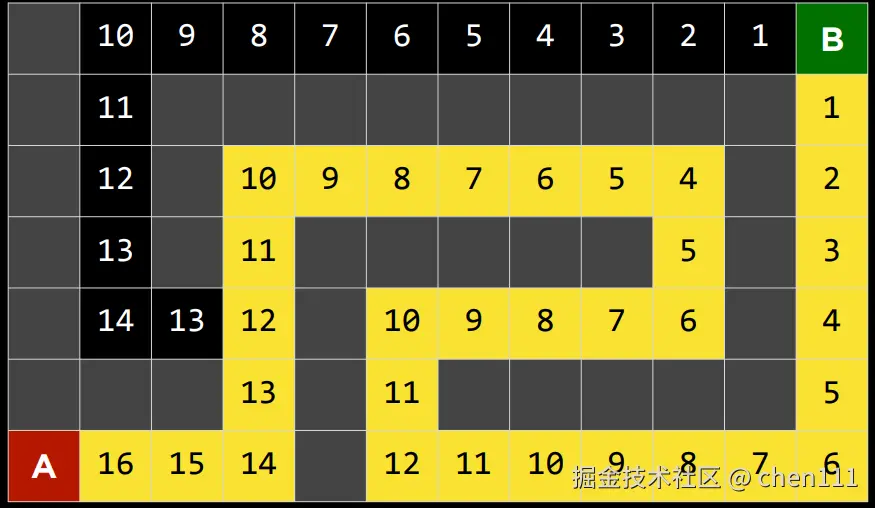夸张地说，贪婪最佳搜索算法不仅没有选择最佳路径，反而选择了最长路径（最坏情况）。这也能体现贪婪算法的特点：选择当前状态下的最佳决策。但有时会错过全局的最佳决策。
可以看到，选择的这条路上的数值先是逐渐减少，后来却在没有分岔口的情况下逐渐增加，或许这就是需要我们优化的痛点。
我们从起点右拐到第二个12的点需要21步，但是左拐到第二个13的点却只需要6步，对于贪婪算法来说，12小于13，所以该选第一个路径。但或许我们可以更聪明一点地想 ------ 如果某个地方按启发式估算看起来离目标稍微远一点，但我实际上能更快到达那里，我宁愿去那个地方。
所以我们不仅需要考虑从当前位置到目标的估计成本，还需要考虑从起点到当前位置的应计成本，这就衍生出另一个算法------ A* 搜索。
A* 搜索（A* Search）
该搜索算法则需要考虑 h(n) 和 g(n) 的和， 其中，g(n) 指的是从起点到当前状态花费的成本，h(c)指当前状态到目标状态需花费的估计成本。
于是，整个过程就变成了这样： 
当右拐后走到 15+6 时，发现左拐第一个点的16+3 的值更小，于是立即转到另一个路口，换句话概括说------A* 会一路记录这个总费用，如果发现现在这条路的 g(n) + h(n) 已经比之前某条候选路线的估算总费用还高，它就会果断放弃当前这条路，回头去走那条更优的路线。这样就避免了被 h(n) 误导。
再强调一次，A* 搜索也是依赖启发式函数的，其效果如何，取决于这个启发式是否适用当前情况。若启发式函数给的方向不靠谱，有时候该算法会比贪心搜索，甚至比那些完全不看启发式的"盲搜"还慢。
当然还有其他的搜索算法对其他情况进行了优化，我们在这只举例这些。
对抗搜索（Adversarial Search）
虽然之前我们已经讨论过需要找到问题答案的算法，但在对抗性搜索中，该算法面对的是试图实现相反目标的对手。通常，在游戏中会遇到使用对抗性搜索的人工智能，例如井字游戏。
所使用的符号连成3个，该方获胜。这种规则是我们人所能理解的，但是如何以"计算机的语言"来表达，我们知道的是，计算机能理解数字，能够判断数字的大小，所以我们就利用这一点，用数字来分配不同状态。
对于这种对抗游戏，结局无非有三种可能：玩家赢、对手赢、平局。所以我们将这些状态赋值，拿井字游戏来说------O赢为-1，X赢为 1，平局为 0 。 所以O方玩家的目标是使得状态对应的值越小 越好，我们将其称为最小玩家；X方玩家的目标是使得状态对应的值越大越好，我们将其称为最大玩家。
这就是极大极小算法的思想之一。
极大极小（Minimax）
极小极大是对抗搜索中的一种算法，将获胜条件表示为一侧的获胜条件为 （-1），另一侧的获胜条件为 （+1）。进一步的行动将由这些条件驱动，最小化的一方试图获得最低的分数，而最大化的一方试图获得最高分数。
在我看来，该算法就是用AI来模拟两个玩家下棋的过程，并举出所有可能性。
所以我们需要通过每一步的状态信息，再一步一步地得出结果。 我们用一些函数来定义游戏规则和状态变化：
- S0 ：初始状态。也就是一开始的棋盘。
- Players(s)：一个函数，输入当前棋盘状态
s，返回轮到哪方下棋。 - Actions(s)：一个函数，输入当前棋盘状态
s，返回所有能走的合法位置（哪些格子是空的）。
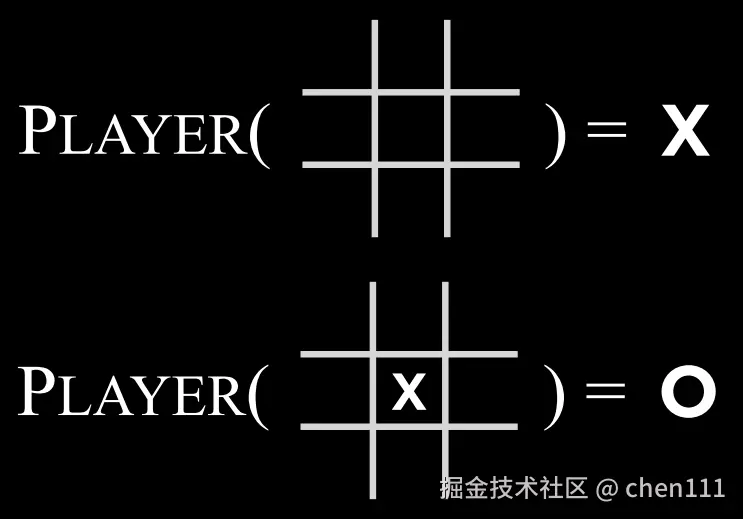
- Result(s, a)：一个函数，输入当前棋盘状态
s和一个动作a，返回在s状态下执行动作a后产生的新的状态。 - Terminal(s)：一个函数，输入当前棋盘状态
s，判断游戏是否结束（结束返回True，反之返回False）。 - Utility(s)：一个函数，输入一个结束状态
s，返回结局对应的值。- 1：X玩家赢
- -1：O玩家赢
- 0：平局
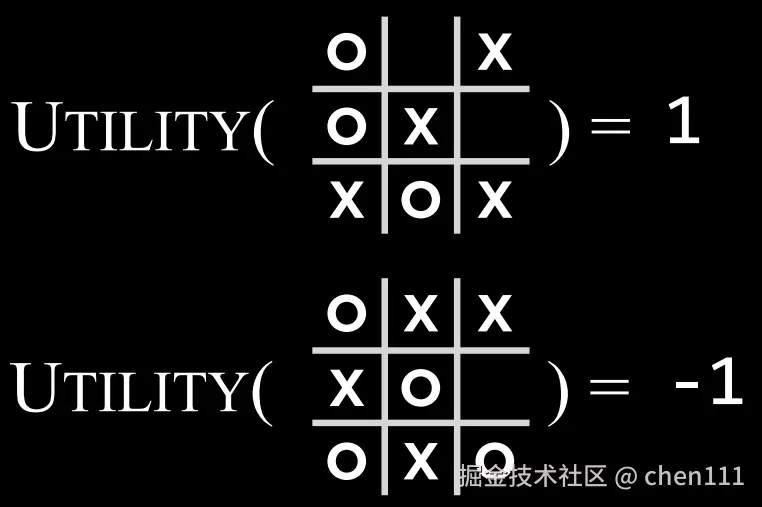
在X玩家的视角模拟从初始状态到最终状态过程中所有的可能性：
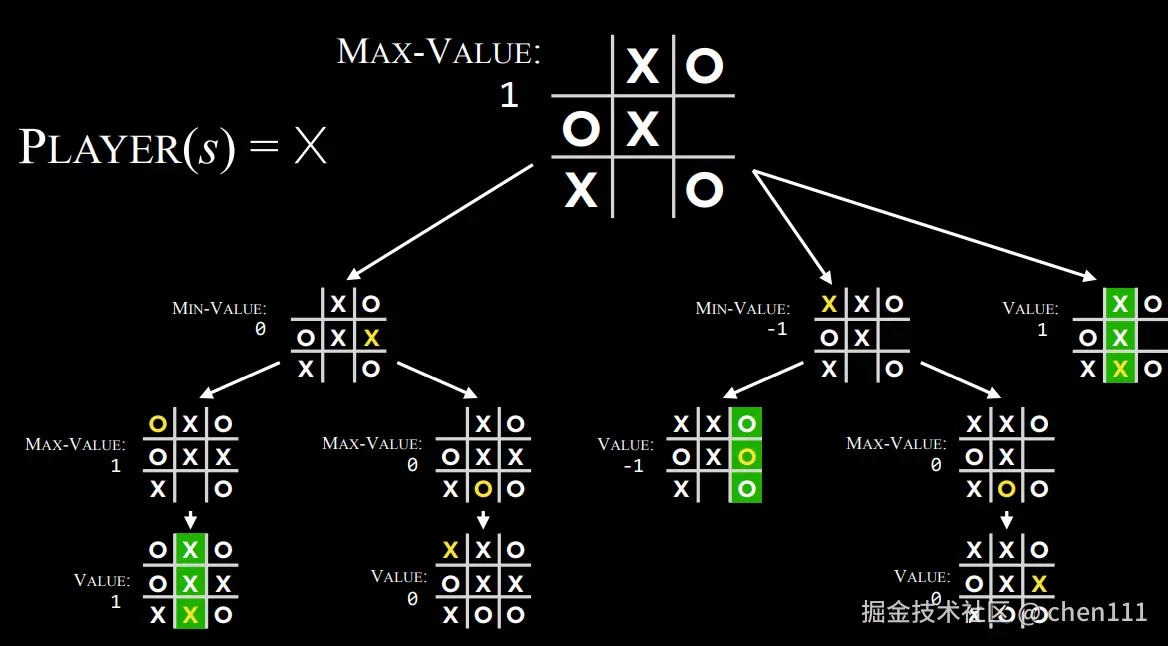再根据最终值来选择走哪一步。
其实除了井字棋游戏，还有其他的对抗游戏，所以我们需要用它们的共同点得出通用的式子------那就是，双方玩家的目的都不变，一方尽力使数值更小，另一方尽力使数值更大。
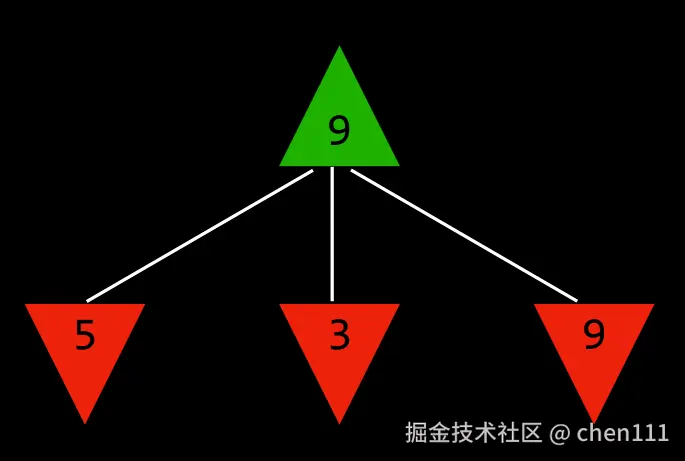上图中，绿色的向上的箭头代表最大玩家，红色的向下箭头代表最小玩家，此时到最大玩家执行动作，有三个选择，选择结果分别是5、3、9，很明显，对于最大玩家来说，选择9是当下最好的打算。
没这么简单，我们还可以预判对方的选择。下图：
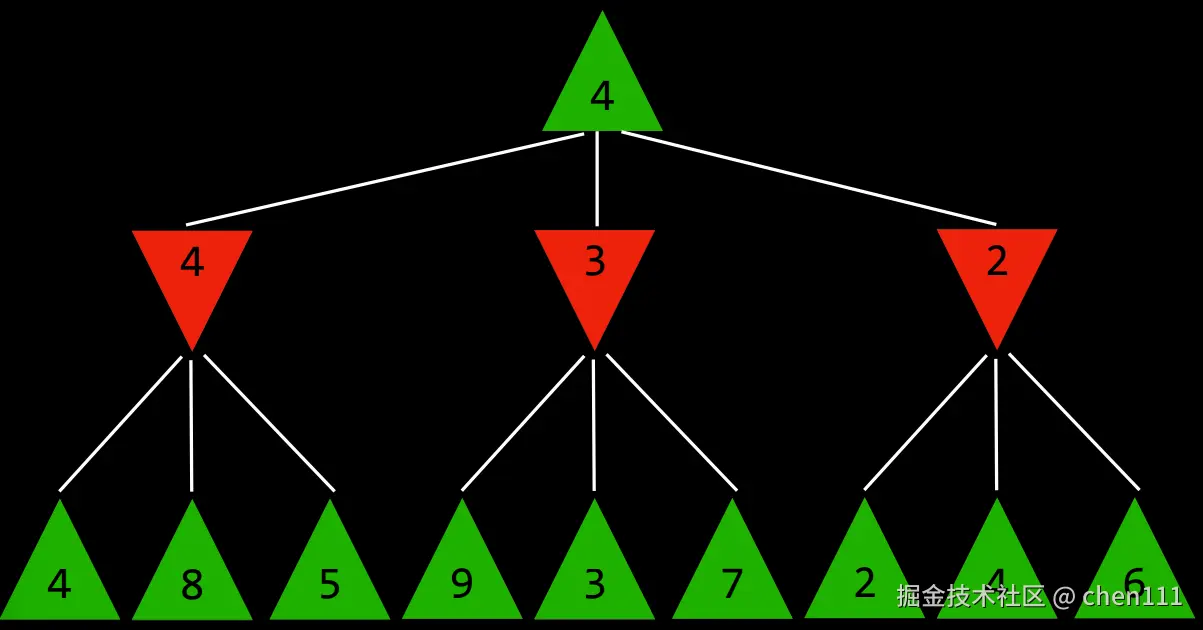我们是最大玩家，现在面临三个选择：4、3、2，若我们选择4，对手则可能选择4、8、5中的一个，按照最坏情况，对手可能选4，以此类推，若我们选3，对手可能选3，若我们选2，对手可能选2，所以，我们若要让分数尽量大，我们就需要选择4。
这种情况需要执行12次才能得出选择4的这个决定。但井字棋一共只有 255,168 种可能的对局过程（从开局到结束的完整走法组合），这是一个极其巨大的数字。
如果遇到比刚才更糟糕的情况呢？难道我们要全部遍历一遍吗？还是说，如何优化？
Alpha-Beta剪枝（Alpha-Beta Pruning）
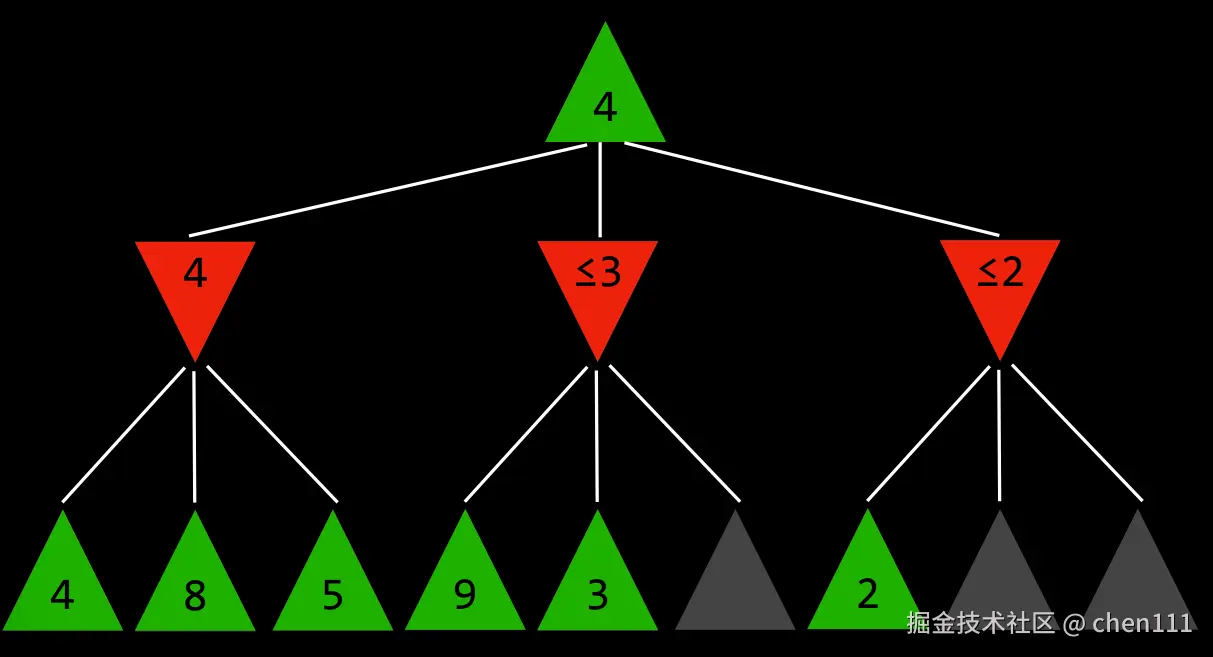由于最大玩家会尽量提高分数，所以第三层的节点的值一定大于其父节点。当我们遍历完4分数的子节点，明白若选择4则最坏的情况下对手会选择4。我们开始遍历分数3的子节点，当遍历到第二个节点3的时候，我们就能知道，剩下的节点分数一定大于等于3，所以最大玩家若选择3，其对手可能会选择3，这个结果比4更差。遍历分数2的子节点也是同理，当我们遍历到第一个子节点2时，由于其父节点是2，所以其剩下的子节点的分数一定大于等于2，最坏的情况下对家就会选择2，比前两个选择结果更差。（注：以上都是从最坏的情况考虑）
经过上面的分析，最大玩家才选择4。这种算法叫做Alpha-Beta剪枝 （Alpha-Beta Pruning ），是采取剪枝措施对Minimax的一种优化。
井字棋的全部可能对局只有 255,168 种 ，而国际象棋的可能对局数大约是 1029000 这么夸张的数量级。
Minimax如果按照最原始的方式运行，需要从当前局面一直穷举到游戏结束的所有可能走法。 井字棋的情况，计算机可以轻松算完，但国际象棋就完全不可能做到。
深度限制极大极小算法
所以我们有了深度限制极大极小算法（Depth-limited Minimax） ------它只计算一个预先设定的步数，然后就停下来，不一定走到游戏真正结束。
问题是，这样停下来时并不知道每个走法的最终结果，所以没法直接给出精确的数值评价。
为了解决这个问题，就引入了评估函数（Evaluation Function） 。
评估函数的作用就是在游戏中途，根据当前局面去估算这个局面对玩家的好坏程度（也就是"效用值"）。
比如在国际象棋里，它会看当前双方的棋子数量、棋子种类、位置等，综合评估谁的形势更好，然后返回一个正数（对一方有利）或负数（对另一方有利）。
这样，Minimax 虽然没走到终局，也能通过评估函数的分数来决定哪个走法更好。评估函数越精准，Minimax 算法做出的选择就越靠谱。