算法奇妙屋(十四)-简单多状态dp问题

少许极端2025-11-27 12:32

文章目录

一. 力扣面试题 17.16. 按摩师

1. 题目

这里题目的意思是这一组数据, 不能选择相邻的数字, 最少间隔一个, 然后求选择数据和的最大值

2. 算法原理

3. 代码

java 复制代码 
    public int massage(int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = nums[0];
        for (int i = 1; i < n; i++) {
            f[i] = g[i- 1] + nums[i];
            g[i] = Math.max(g[i - 1], f[i - 1]);
        }
        return Math.max(f[n - 1], g[n - 1]);
    }

二. 力扣LCR 090. 打家劫舍 II

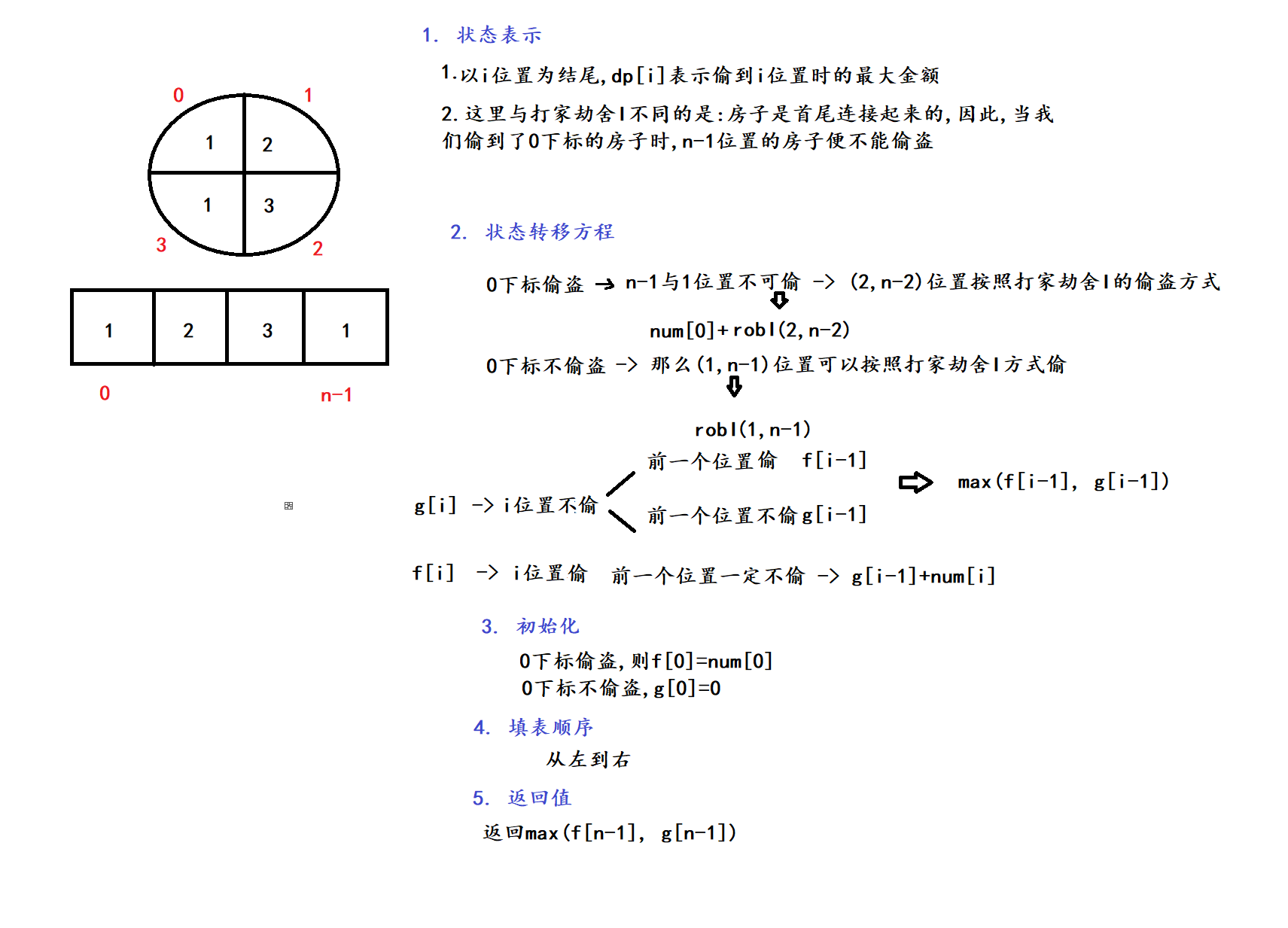
1. 题目

相比于打家劫舍I(上一道题和打家劫舍I解法一样), 这里的房子只是变为了环形

2. 算法原理

3. 代码

java 复制代码 
    public int rob(int[] nums) {
        int n = nums.length;
        // 0 偷
        int t1 = robI(nums, 2, n - 2) + nums[0];
        // 0 不偷
        int t2 = robI(nums, 1, n - 1);
        return Math.max(t1, t2);
    }

    public int robI(int[] nums, int start, int end) {
        if (start > end) {
            return 0;
        }
        int n = nums.length;
        int[] f = new int[n];
        int[] g = new int[n];
        f[start] = nums[start];
        for (int i = start + 1; i <= end; i++) {
            f[i] = g[i - 1] + nums[i];
            g[i] = Math.max(f[i - 1], g[i - 1]);
        }
        return Math.max(f[end], g[end]);
    }

三. 力扣740. 删除并获得点数

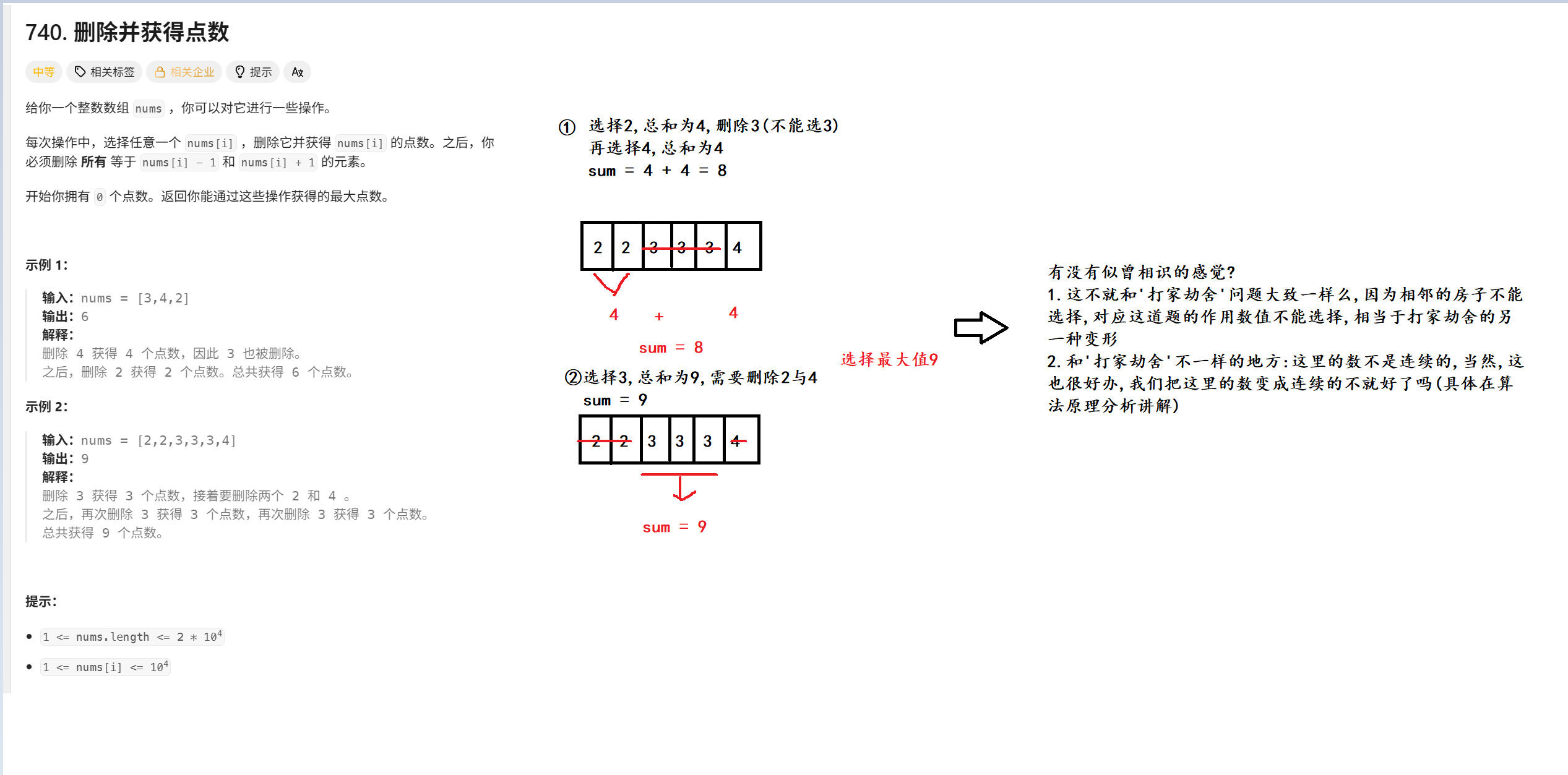
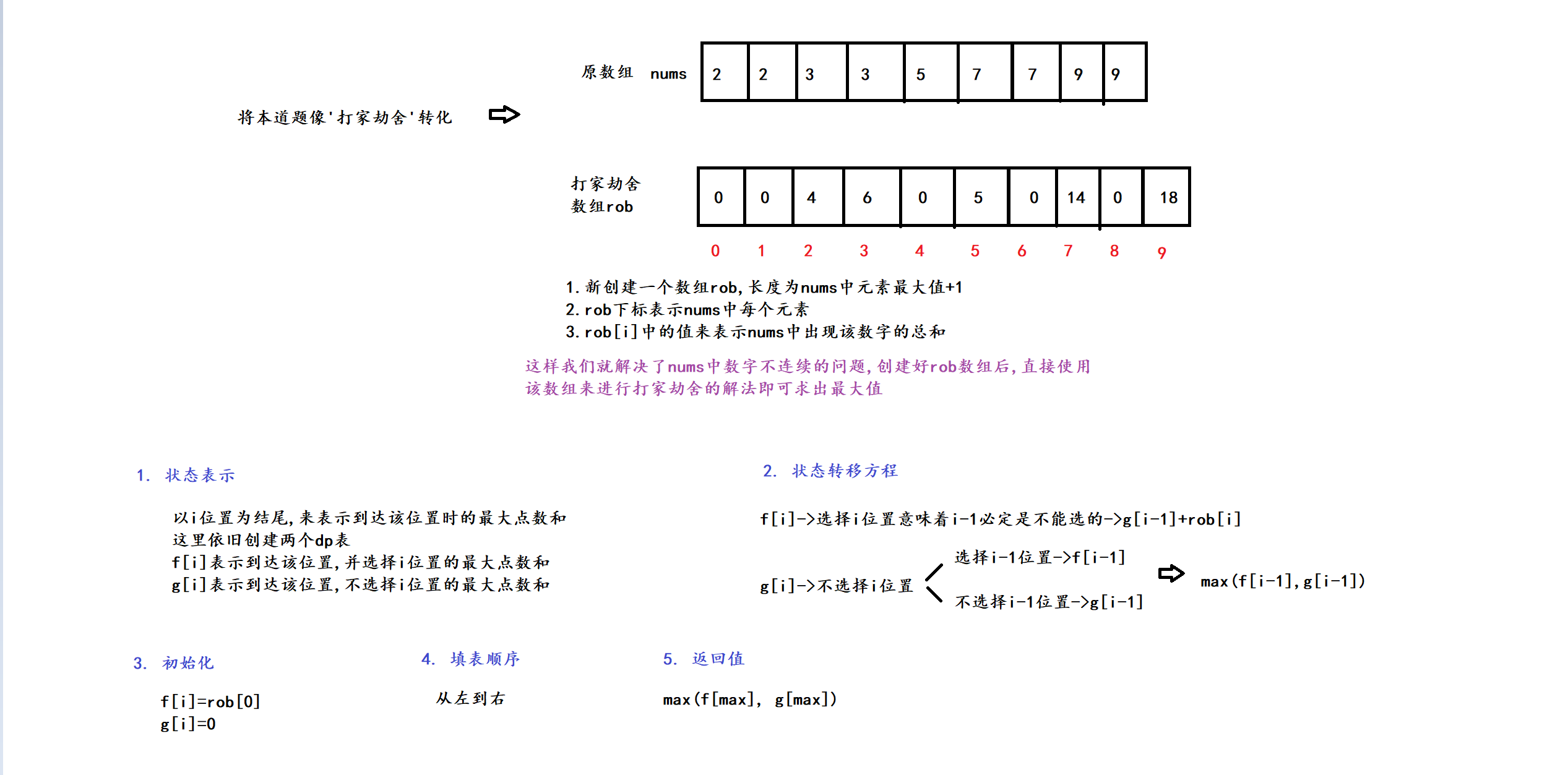
1. 题目

2. 算法原理

3. 代码

java 复制代码 
    public int deleteAndEarn(int[] nums) {
        int[] rob = new int[10001];
        int max = 0;
        for (int x : nums) {
            if (x > max) {
                max = x;
            }
            rob[x] += x;
        }
        int[] f = new int[max + 1];
        int[] g = new int[max + 1];
        f[0] = rob[0];
        for (int i = 1; i <= max; i++) {
            f[i] = g[i - 1] + rob[i];
            g[i] = Math.max(f[i - 1], g[i - 1]);
        }
        return Math.max(f[max], g[max]);
    }

四. 力扣LCR 091. 粉刷房子

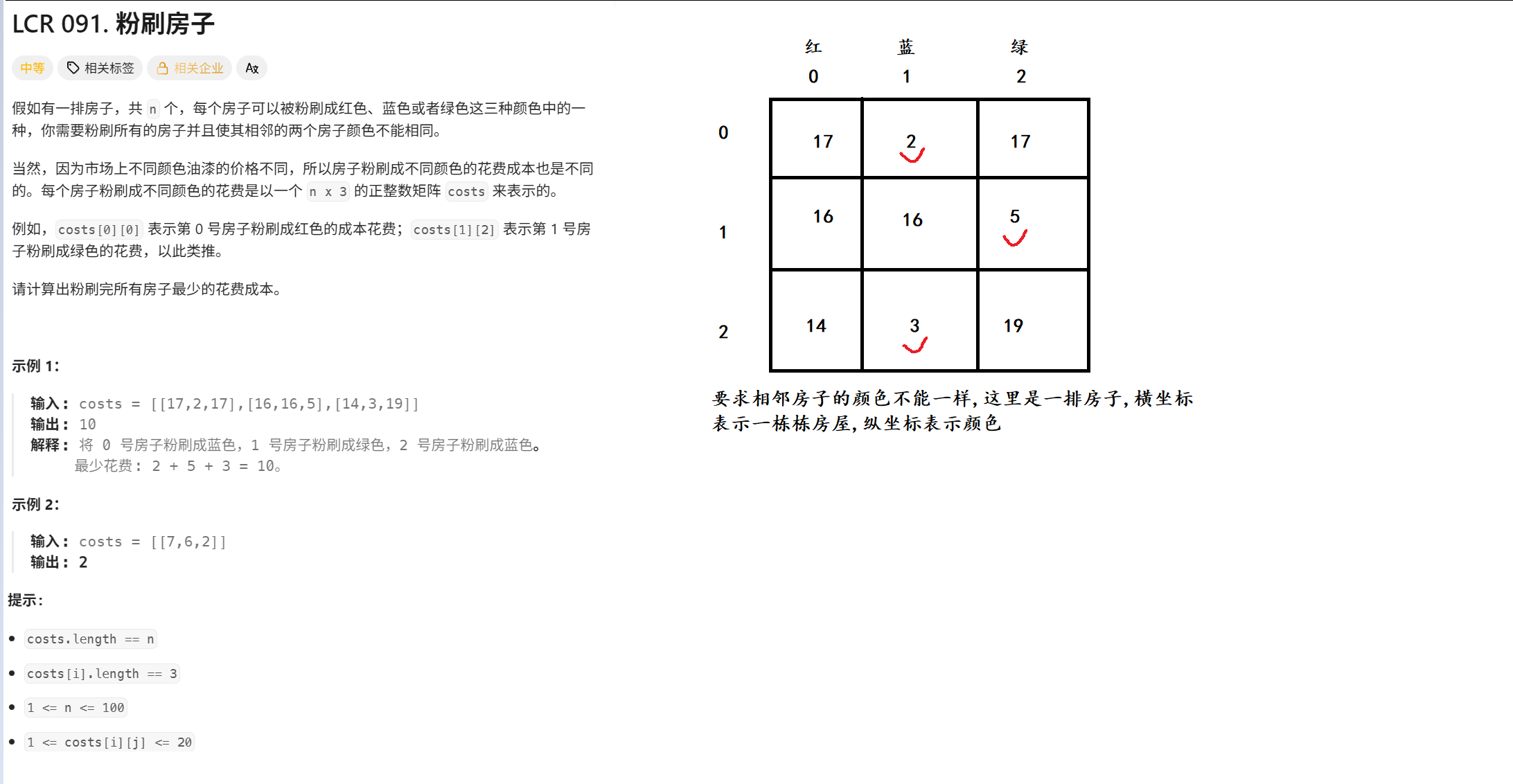
1. 题目

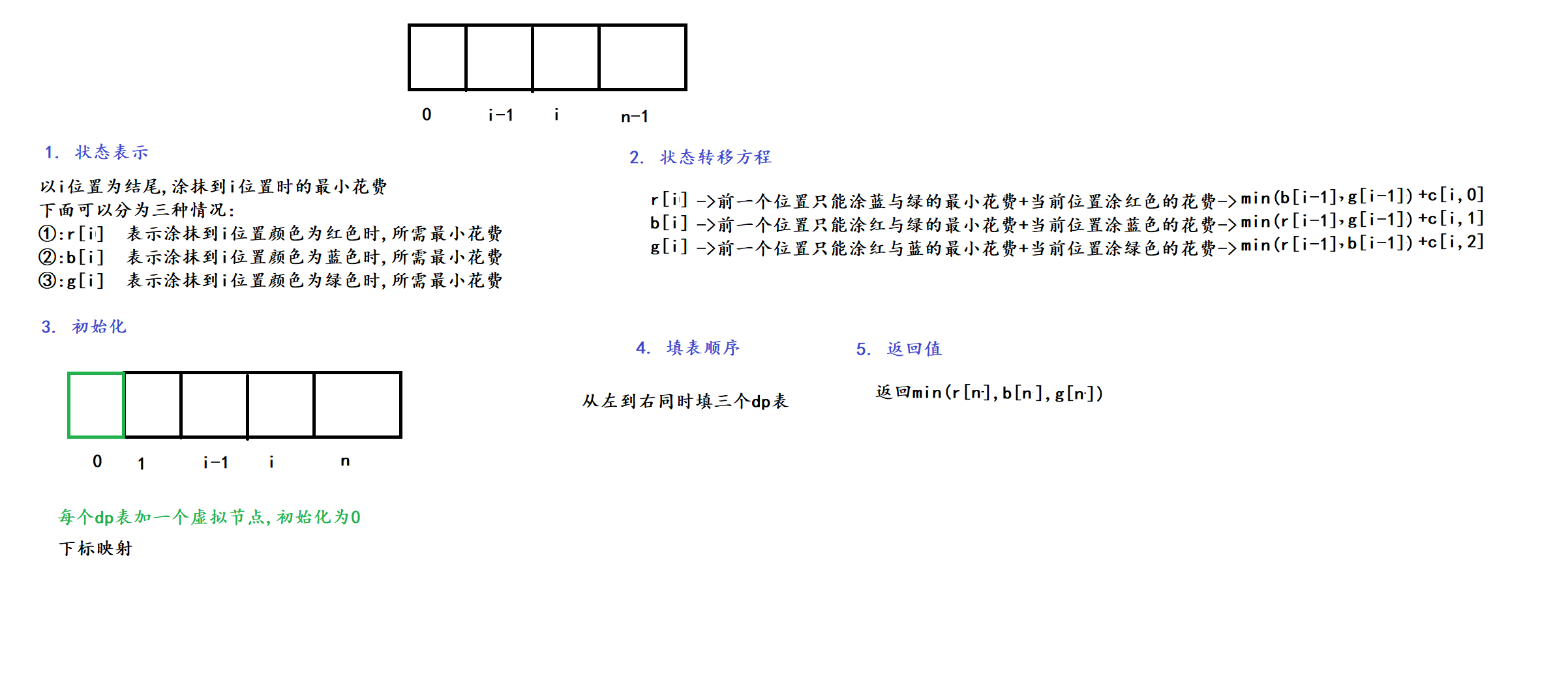
2. 算法原理

3. 代码

java 复制代码 
    public int minCost(int[][] costs) {
        int n = costs.length;
        int[] r = new int[n + 1];
        int[] b = new int[n + 1];
        int[] g = new int[n + 1]; 
        for (int i = 1; i <= n; i++) {
            r[i] = Math.min(b[i - 1], g[i - 1]) + costs[i - 1][0];
            b[i] = Math.min(r[i - 1], g[i - 1]) + costs[i - 1][1];
            g[i] = Math.min(b[i - 1], r[i - 1]) + costs[i - 1][2];
        }
        return Math.min(r[n],Math.min(b[n], g[n]));
    }

五. 力扣309. 买卖股票的最佳时机含冷冻期

1. 题目

2. 算法原理

小编参悟这道题也是参悟了2个小时,才弄懂, 只能第一次见到题解的时候云里雾里, 后来多想了想, 才弄明白一些隐含条件, 一些注意事项都写到了下面图解里

3. 代码

java 复制代码 
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] dp = new int[n][3];
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]);
            dp[i][1] = dp[i - 1][0] + prices[i];
            dp[i][2] = Math.max(dp[i - 1][1], dp[i - 1][2]);
        }
        return Math.max(dp[n - 1][1], dp[n - 1][2]);
    }

六. 力扣714. 买卖股票的最佳时机含手续费

1. 题目

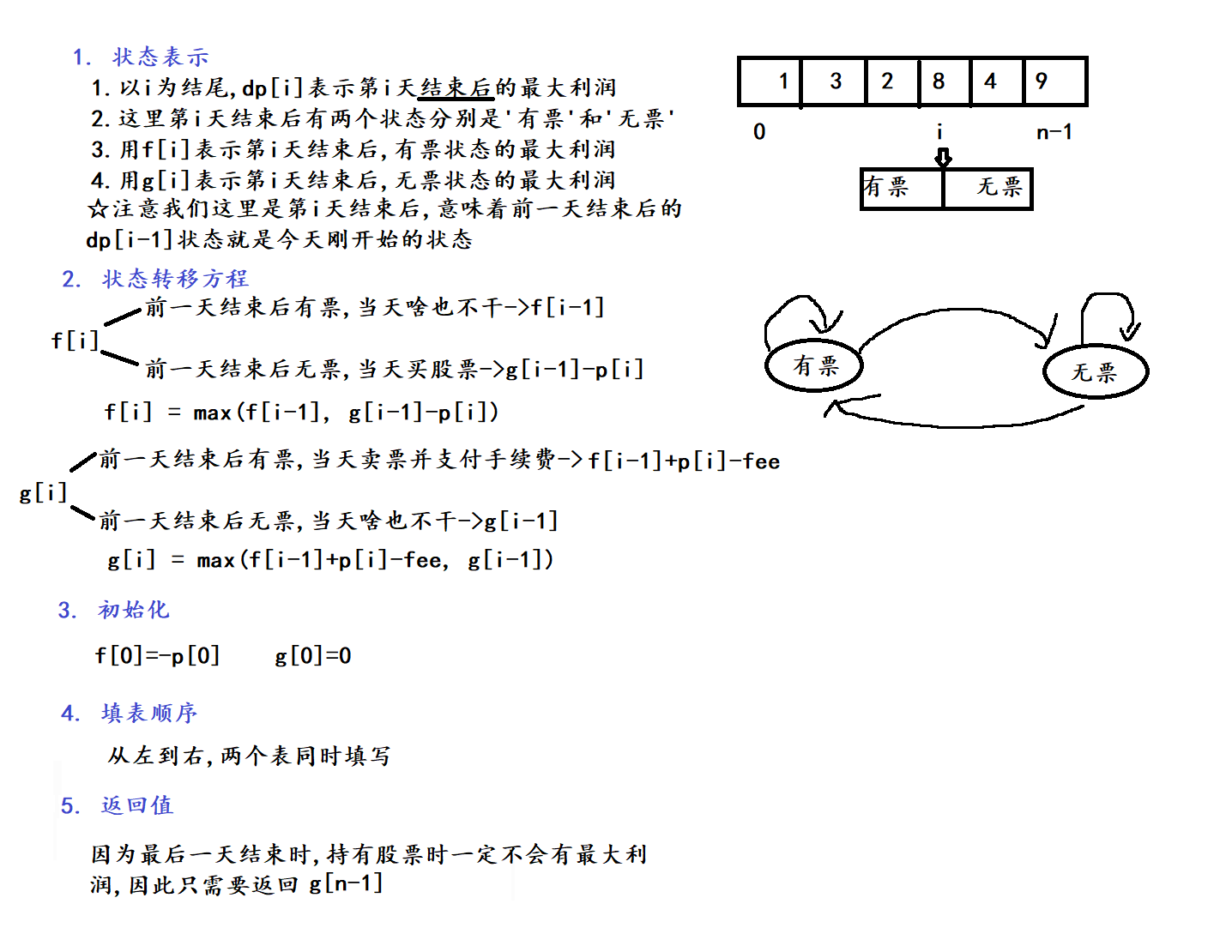
2. 算法原理

3. 代码

java 复制代码 
    public int maxProfit(int[] prices, int fee) {
        int n = prices.length;
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = -prices[0];
        for (int i = 1; i < n; i++) {
            f[i] = Math.max(f[i - 1], g[i - 1] - prices[i]);
            g[i] = Math.max(f[i - 1] + prices[i] - fee, g[i - 1]);
        }
        return g[n - 1];
    }

七. 力扣123. 买卖股票的最佳时机 III

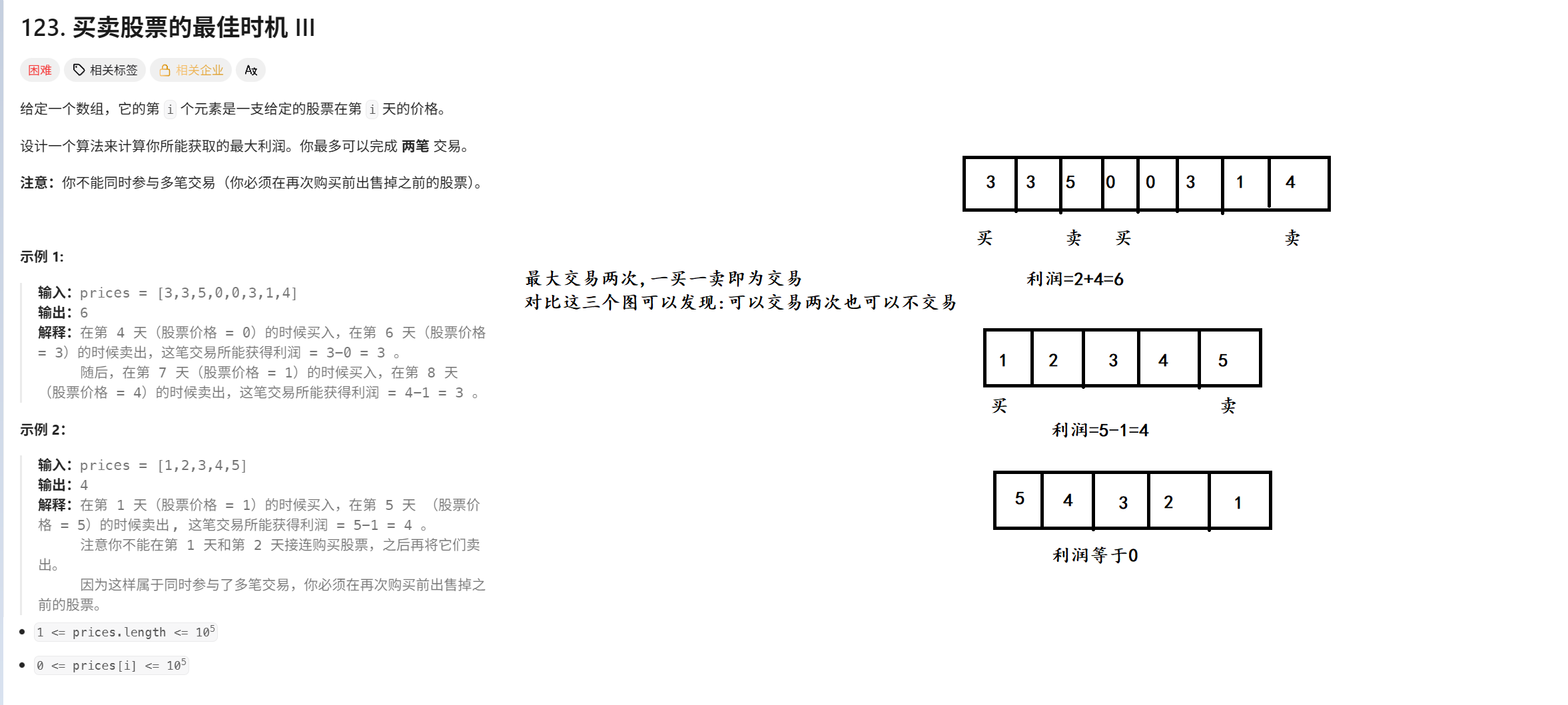
1. 题目

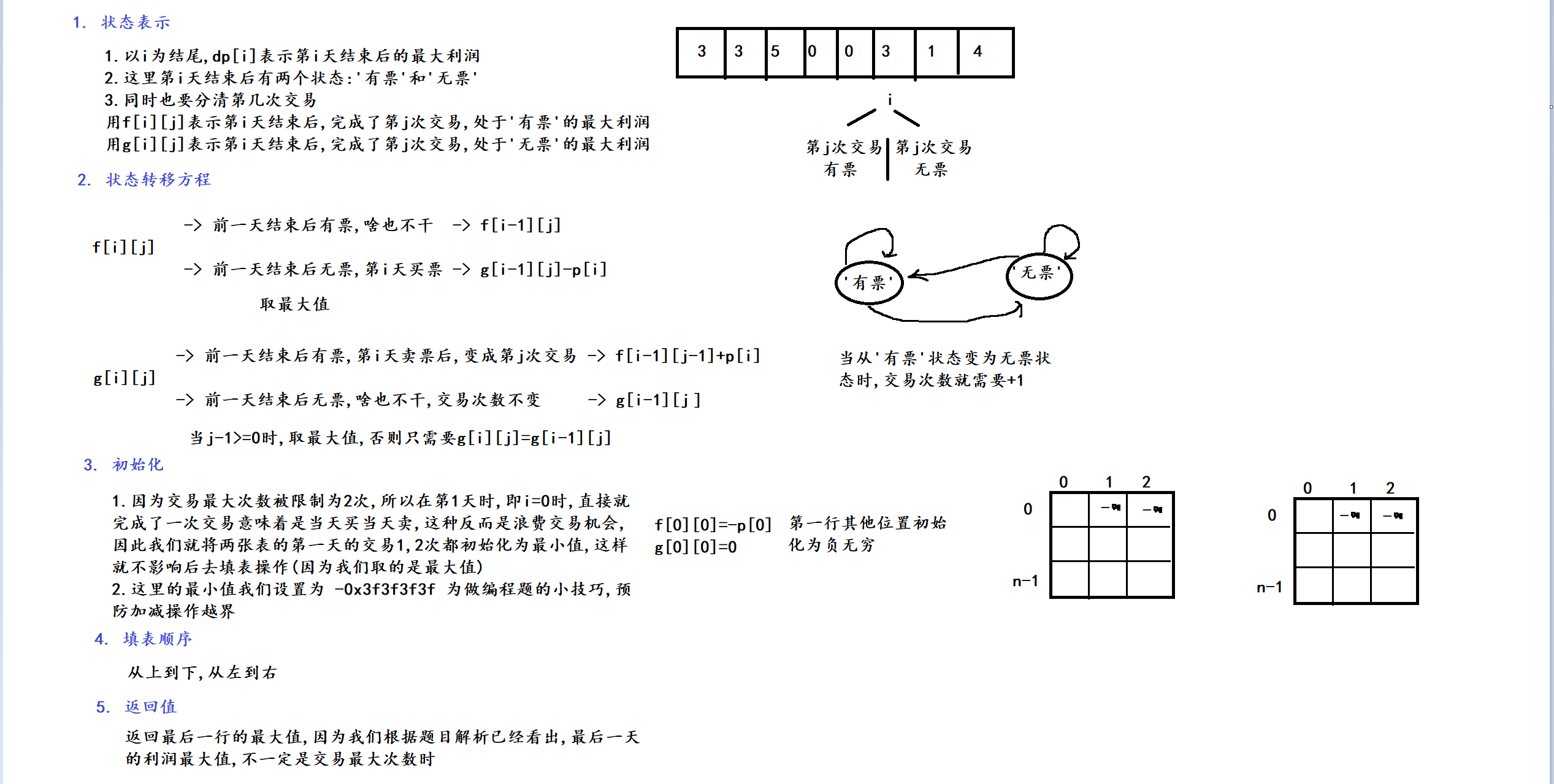
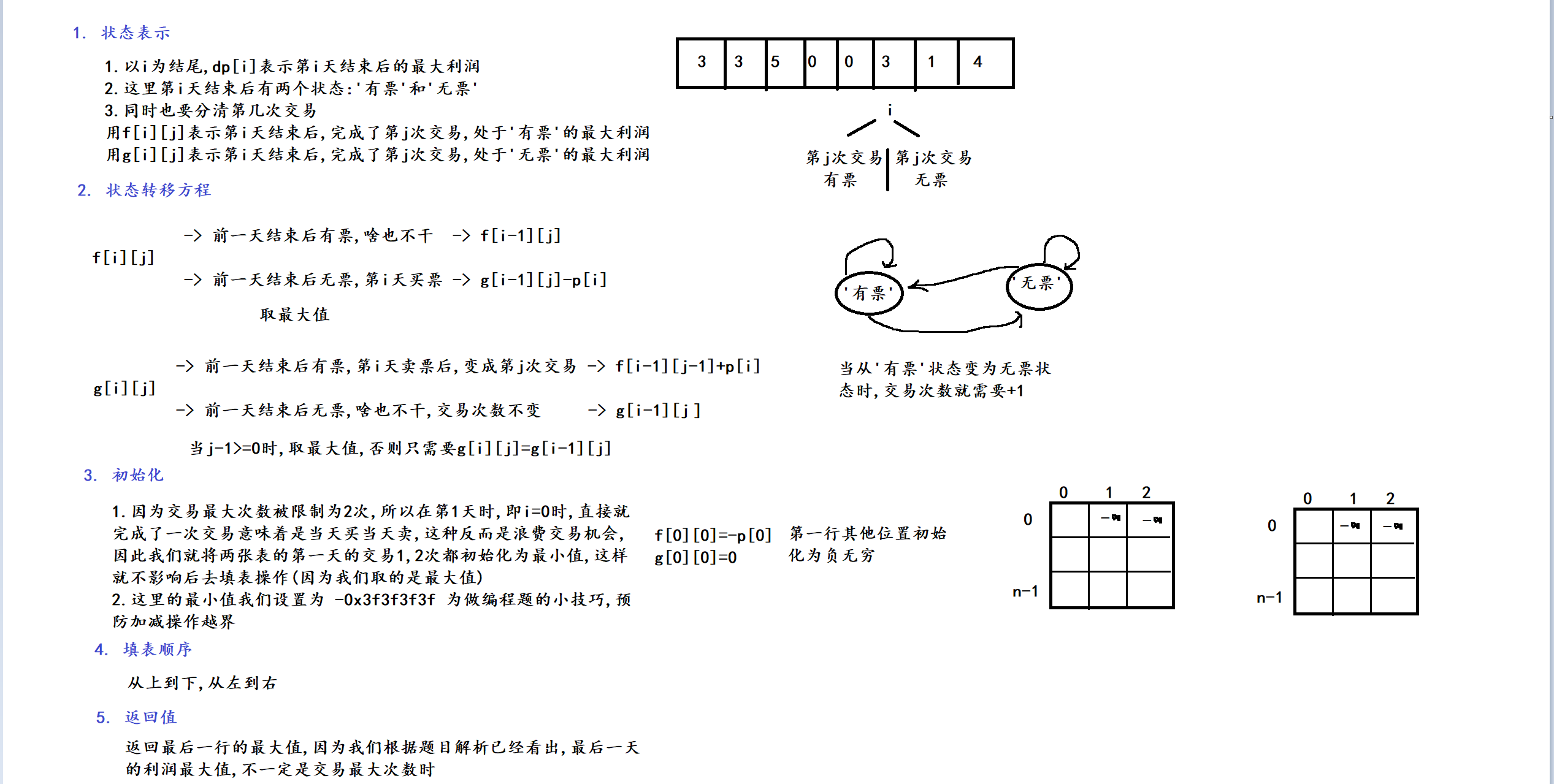
2. 算法原理

3. 代码

java 复制代码 
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] f = new int[n][3];
        int[][] g = new int[n][3];
        f[0][0] = -prices[0];
        f[0][1] = f[0][2] = g[0][1] = g[0][2] = -0x3f3f3f3f;
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < 3; j++) {
                f[i][j] = Math.max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if (j - 1 >= 0) {
                    g[i][j] = Math.max(g[i][j], f[i - 1][j - 1] + prices[i]);
                }
            }
        }
        return Math.max(g[n - 1][0], Math.max(g[n - 1][1], g[n - 1][2]));
    }

八. 力扣188. 买卖股票的最佳时机 IV

1. 题目

相较于上一道题,这里的最大交易两次变为了k次, 但是丝毫不慌, 因为我们上一道题提供的解法是通用的, 不管你最大限制交易多少次, 都是一样的解法

2. 算法原理

因为我们上一道题的解法和这道题一模一样, 这里我就懒一下,不过多赘述, 直接从上面讲解法复制下来了, 同样也是方便大家观看

3. 代码

java 复制代码 
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
        int[][] f = new int[n][k + 1];
        int[][] g = new int[n][k + 1];
        for (int j = 1; j <= k; j++) {
            f[0][j] = g[0][j] = -0x3f3f3f3f;
        }
        f[0][0] = -prices[0];
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= k; j++) {
                f[i][j] = Math.max(f[i - 1][j], g[i - 1][j] - prices[i]);
                if (j - 1 >= 0) {
                    g[i][j] = Math.max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);
                }else {
                    g[i][j] = g[i - 1][j];
                }
            }
        }
        int max = 0;
        for (int j = 0; j <= k; j++) {
            if (g[n - 1][j] > max) {
                max = g[n - 1][j];
            }
        }
        return max;
    }
相关推荐
2401_857683547 分钟前
C++代码静态检测
开发语言·c++·算法
时艰.12 分钟前
JVM 垃圾收集器（G1&ZGC）
java·jvm·算法
2401_8384725112 分钟前
内存泄漏自动检测系统
开发语言·c++·算法
m0_7066532330 分钟前
基于C++的爬虫框架
开发语言·c++·算法
diediedei37 分钟前
嵌入式数据库C++集成
开发语言·c++·算法
君义_noip39 分钟前
洛谷 P3388 【模板】割点（割顶）
c++·算法·图论·信息学奥赛·csp-s
xie0510_39 分钟前
string模拟实现
开发语言·c++·算法
xuedingbue1 小时前
数据结构与顺序表：高效数据管理秘籍
数据结构·算法·链表
星火开发设计1 小时前
共用体 union：节省内存的特殊数据类型
java·开发语言·数据库·c++·算法·内存
求梦8201 小时前
【力扣hot100题】合并两个有序链表（22）
算法·leetcode·链表
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）04Clawdbot 中文汉化版 接入微信、飞书05Claude Code Skills 实用使用手册06在Trae中使用Pencil MCP07struts2 XML外部实体注入漏洞复现（CVE-2025-68493）08UV安装并设置国内源09零门槛部署本地 AI 助手：Clawdbot/Meltbot 部署深度保姆级教程10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南