文章目录
- Subsets
-
- Resources
- [Solution - Apple Division](#Solution - Apple Division)
-
- [递归生成子集Generating Subsets Recursively](#递归生成子集Generating Subsets Recursively)
- [二进制枚举子集Generating Subsets with Bitmasks](#二进制枚举子集Generating Subsets with Bitmasks)
- Permutations
-
- [Solution - Creating Strings I](#Solution - Creating Strings I)
- 回溯Backtracking
Subsets
问题-problem
Resources
完全搜索
完全搜索(Complete search)是一种通用方法,可以用来解决几乎任何算法问题。
它的思想是通过穷举法生成问题的所有可能解,然后根据题目要求,要么选出最优解,要么统计解的数量。
如果有足够的时间遍历所有解,完全搜索是一种很好的技巧,因为它通常容易实现,并且一定能给出正确答案。
如果完全搜索太慢,就需要使用其他方法,例如贪心算法或动态规划。
5.1 生成子集
我们先考虑一个问题:生成一个 n n n 元集合的所有子集。
例如,集合: ∅, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}
生成子集有两种常用方法:
-
使用递归搜索
-
利用整数的二进制表示
方法一:递归生成
一种优雅的方式是使用递归。下面的函数 search 用来生成集合 {0,1,...,n−1} 的所有子集。
函数维护一个向量 subset,保存当前子集的元素。搜索从 search(0) 开始。
cpp
void search(int k)
{
if (k == n)
{
// 处理当前子集
} else
{
search(k+1); // 不选 k
subset.push_back(k); // 选 k
search(k+1);
subset.pop_back(); // 回溯
}
}当 search(k) 被调用时,它决定是否将元素 k k k 放入子集中,然后在两种情况下都调用 search(k+1)。
如果 k == n,说明所有元素都已处理完,一个子集已生成。
递归调用树(n=3 时),在每一步,我们可以选择左分支(不选 k k k)或右分支(选 k k k):
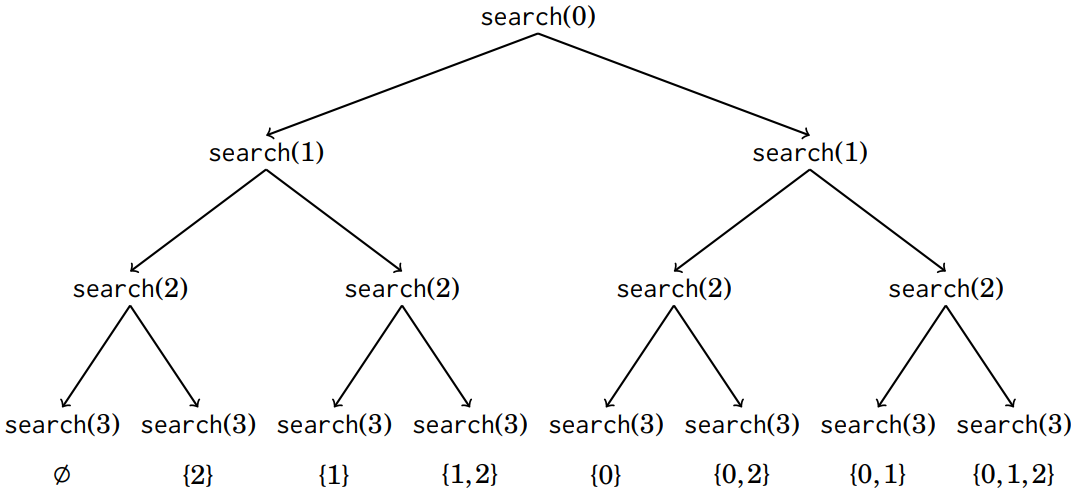
方法二:二进制枚举
另一种方法是利用整数的二进制表示。
一个 n n n 元集合的每个子集都可以表示为 n n n 位的二进制数(bit 序列),对应一个 0 0 0 到
2 n − 1 2^n - 1 2n−1 的整数。在该 bit 序列中, 1 1 1 表示对应元素被选入子集。
例如,整数 25 25 25 的二进制表示是 11001,对应的子集是 {0,3,4}。
遍历所有子集的代码如下:
cpp
for (int b = 0; b < (1<<n); b++)
{
// 处理子集 b
}如果想获取子集的具体元素,可以这样写:
cpp
for (int b = 0; b < (1<<n); b++)
{
vector<int> subset;
for (int i = 0; i < n; i++)
{
if (b & (1<<i)) subset.push_back(i);
}
// subset 现在就是 b 对应的子集
}Solution - Apple Division
由于 n ≤ 20 n≤20 n≤20,我们可以通过尝试所有可能的将 n n n 个苹果分成两组的方式,来找到重量差最小的分法。这里有两种实现方法。
递归生成子集Generating Subsets Recursively
第一种方法是编写一个递归函数来遍历所有可能的情况。
在某个下标位置,我们要么将 w e i g h t i weight_i weighti 加入第一组,要么加入第二组,同时分别用 s u m 1 sum_1 sum1 和 s u m 2 sum_2 sum2 记录两组的重量和。
当我们遍历到数组末尾时,就返回两组重量之差。
cpp
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int n;
vector<long long> weights;
ll recurse_apples(int index, ll sum1, ll sum2) {
// 已经分配完所有苹果 ------ 返回两组重量的绝对差
if (index == n) { return abs(sum1 - sum2); }
// 尝试将当前苹果加入第一组或第二组,取差值较小的情况
return min(recurse_apples(index + 1, sum1 + weights[index], sum2),
recurse_apples(index + 1, sum1, sum2 + weights[index]));
}
int main() {
cin >> n;
weights.resize(n);
for (int i = 0; i < n; i++) { cin >> weights[i]; }
// 从第 0 个苹果开始,两组均为空,递归求解
cout << recurse_apples(0, 0, 0) << endl;
}二进制枚举子集Generating Subsets with Bitmasks
位掩码(bitmask)是一个整数,它的二进制表示用来表示一个子集。
在本题中,如果某个位掩码的第 i i i 位等于 1 1 1,我们就说第 i i i 个苹果在 s 1 s_1 s1 中;否则,就认为它在 s 2 s_2 s2 中。
如果我们遍历所有从 0 0 0 到 2 N − 1 2^N - 1 2N−1 的位掩码,就能枚举出 s 1 s_1 s1 的所有子集。
我们用 N = 3 N = 3 N=3 来做一个快速演示:
下面列出了从 0 0 0 到 2 3 − 1 2^3 - 1 23−1 的所有整数、它们对应的二进制表示,以及对应的 s 1 s_1 s1 中包含的元素。
可以看到,所有可能的子集都被涵盖到了。
| Number | Binary | Apples in s 1 s_1 s1 |
|---|---|---|
| 0 | 000 | { } \{\} {} |
| 1 | 001 | { 0 } \{0\} {0} |
| 2 | 010 | { 1 } \{1\} {1} |
| 3 | 011 | { 0 , 1 } \{0,1\} {0,1} |
| 4 | 100 | { 2 } \{2\} {2} |
| 5 | 101 | { 0 , 2 } \{0,2\} {0,2} |
| 6 | 110 | { 1 , 2 } \{1,2\} {1,2} |
| 7 | 111 | { 0 , 1 , 2 } \{0,1,2\} {0,1,2} |
有了这个概念,我们就可以实现解法了。
你会注意到我们的代码中有一些花哨的按位操作:
-
1 << x对于整数 x x x 来说,这是另一种表示 2 x 2^x 2x 的写法,在二进制中只有第 x x x 位是
1(其余位都是0)。 -
&(按位与)操作符对两个整数做逐位比较:对于整数 a a a 和 b b b,表达式
a & b会返回一个新整数,其第 i i i 位仅在 a a a 和 b b b 的第 i i i 位都为1时才是1。
因此,mask & (1 << x) 只有在 mask 的第 x x x 位被置为 1 时才会返回一个非零(正)值。
cpp
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
int n;
cin >> n;
vector<ll> weights(n);
for (ll &w : weights) { cin >> w; }
ll ans = INT64_MAX;
for (int mask = 0; mask < (1 << n); mask++) {
ll sum1 = 0;
ll sum2 = 0;
for (int i = 0; i < n; i++) {
// 检查第 i 位是否被置位
if (mask & (1 << i)) {
// 如果是,则该苹果属于第一组 sum1
sum1 += weights[i];
} else {
sum2 += weights[i];
}
}
ans = min(ans, abs(sum1 - sum2));
}
cout << ans << endl;
}Permutations
排列(Permutation) 是对一组元素的重新排序。
问题-problem
想想字典里单词是如何排序的。(实际上,"lexicographical"(字典序)一词就是由此而来。)
在字典中,所有以字母 a a a 开头的单词出现在最前面,接着是以字母 b b b 开头的单词,依此类推。
如果两个单词首字母相同,则比较第二个字母;如果第一、第二个字母都相同,则比较第三个字母,依此类推,直到遇到不同的字母,或者一个单词结束(这时较短的单词排在前面)。
排列的字典序排列方式几乎相同。
我们先按排列的第一个元素分组;如果两个排列的第一个元素相同,则比较第二个元素;如果第二个元素也相同,则比较第三个,以此类推。
例如, 3 3 3 个元素的排列按字典序排列为:
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] 。
注意,这个排列列表以第一个元素为 1 1 1 的排列开始(就像字典中以 a a a 开头的单词排在最前),然后是以 2 2 2 开头的,接着是以 3 3 3 开头的。在相同第一个元素的组内,再用第二个元素比较排序。
通常情况下,除非题目特别要求求出字典序最小或最大的解,否则不必担心排列是否按字典序生成。
不过字典序的概念在编程竞赛题目中经常出现,且涉及多种场景,建议你熟悉其定义。
有些题目要求对元素进行满足特定条件的排序。
对于这类问题,如果 ( N ≤ 10 N \leq 10 N≤10 ),我们可以直接遍历所有 ( N ! = N × ( N − 1 ) × ⋯ × 1 N! = N \times (N-1) \times \cdots \times 1 N!=N×(N−1)×⋯×1 ) 个排列,检查每个排列是否满足条件。
Solution - Creating Strings I
Resources
我们考虑一个问题:生成一个包含 n n n 个元素的集合的所有排列。
例如,集合 {0,1,2} 的所有排列为:(0,1,2), (0,2,1), (1,0,2), (1,2,0), (2,0,1), (2,1,0)
我们有两种方法可以完成这个任务:
-
使用递归
-
使用迭代(通过不断构造"下一个排列")
方法一:递归生成排列
与子集(subsets)类似,排列也可以通过递归来生成。
下面是一个函数 search(),它生成 {0,1,...,n−1} 的所有排列:
cpp
void search() {
if (permutation.size() == n)
{
// 处理排列结果(例如打印)
} else
{
for (int i = 0; i < n; i++)
{
if (chosen[i]) continue; // 如果已经选择过了,就跳过
chosen[i] = true; // 选中第 i 个元素
permutation.push_back(i); // 加入当前排列
search(); // 递归生成下一层
chosen[i] = false; // 回溯:取消选择
permutation.pop_back(); // 回溯:移除元素
}
}
}方法二:使用 next_permutation 迭代生成排列
另一种生成排列的方法是:
从初始排列 {0,1,...,n−1} 开始,使用一个函数反复生成"字典序下一个排列"。
C++ 标准库提供了 next_permutation 函数,可以用如下方式使用它:
cpp
vector<int> permutation;
for (int i = 0; i < n; i++)
{
permutation.push_back(i); // 初始化为最小字典序排列
}
do
{
// 处理排列结果
} while (next_permutation(permutation.begin(), permutation.end()));回溯Backtracking
问题-problem
Resources
一个回溯算法从一个空的解开始,并一步步扩展这个解。搜索过程会递归地遍历构造一个解的所有不同方式。
例如,考虑这样一个问题:计算将 n n n 个皇后放置在一个 n × n n×n n×n 的国际象棋棋盘上,使得任意两个皇后都不会互相攻击的摆放方案总数。例如,当 n = 4 n = 4 n=4 时,有两种合法的摆放方案:
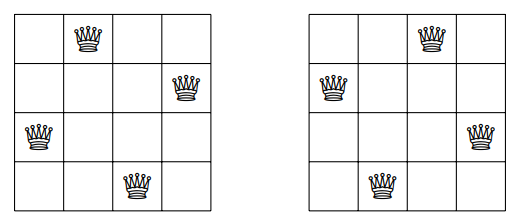
这个问题可以使用回溯算法来解决:每次尝试在棋盘的一行中放置一个皇后。
更具体地说,在每一行放置恰好一个皇后,并确保这个皇后不会攻击到之前已经放置的任何一个皇后。当所有 n n n 个皇后都被成功放置后,说明我们找到了一种可行解。
以 n = 4 n=4 n=4 为例,回溯算法生成的一些中间(部分)状态如下所示:
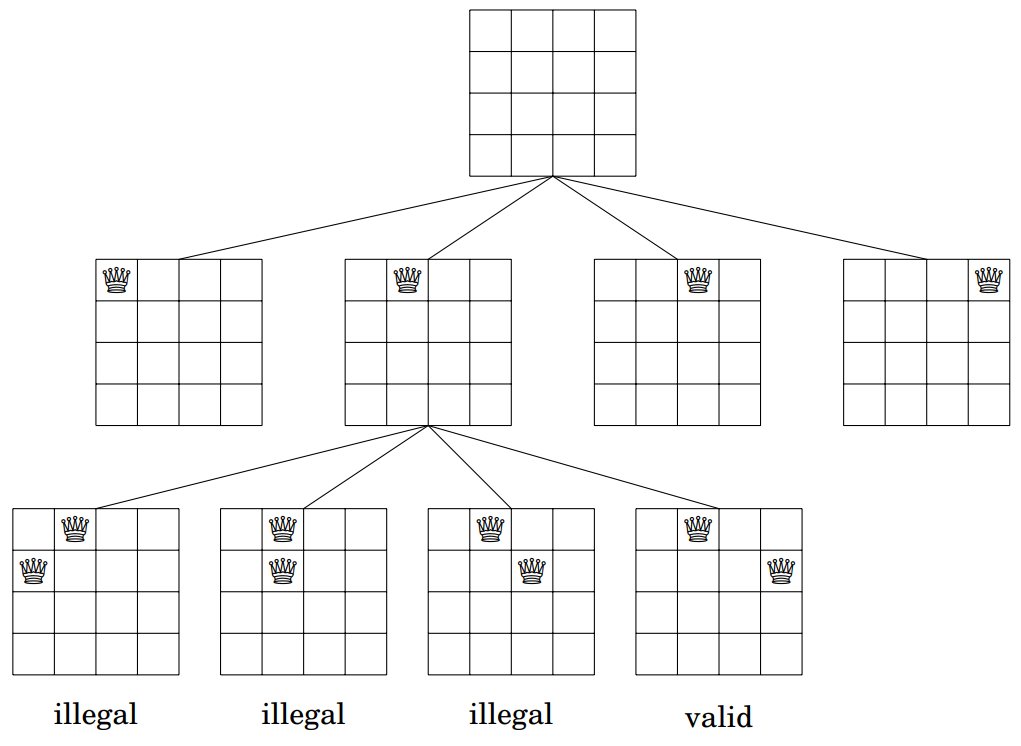
在底部的几种情况中,前三种是非法的,因为皇后之间存在攻击关系。
但第四种是合法的,可以继续扩展,在棋盘上放置剩下的两个皇后。只有一种方式可以完成这个扩展。
这个算法可以通过如下代码来实现:
cpp
void search(int y)
{
if (y == n)
{
count++;
return;
}
for (int x = 0; x < n; x++)
{
if (column[x] || diag1[x+y] || diag2[x-y+n-1]) continue;
column[x] = diag1[x+y] = diag2[x-y+n-1] = 1;
search(y+1);
column[x] = diag1[x+y] = diag2[x-y+n-1] = 0;
}
}搜索过程从 search(0) 开始。棋盘的大小为 n × n,代码通过回溯方法将所有合法解的数量保存在变量 c o u n t count count 中。
代码假设棋盘的行和列编号从 0 0 0 到 n − 1 n − 1 n−1。当函数 search 被调用时,它会尝试在第 y y y 行放置一个皇后,然后递归调用自己放置第 y + 1 y+1 y+1 行的皇后。如果此时 y = n y=n y=n,说明所有皇后都已经成功放置,找到一个解,于是 count++。
数组 column 用于记录哪些列已经有皇后,数组 diag1 和 diag2 用于记录两个方向的对角线上是否已经有皇后。不能将皇后放在已经被其他皇后控制的列或对角线上。例如,4×4 棋盘中列和对角线编号方式如下:
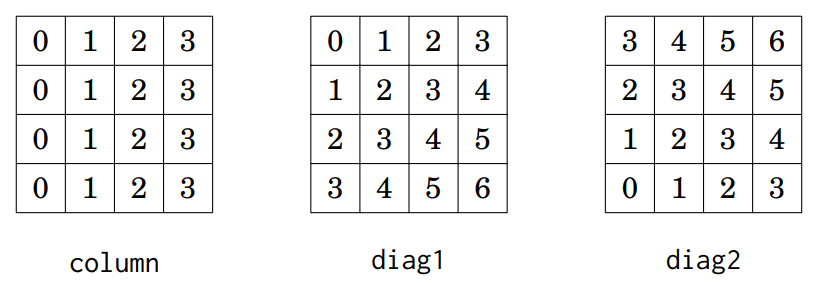
全排列思想解决八皇后问题
一个暴力破解的解法是检查所有 ( 64 8 ) \binom{64}{8} (864) 种可能的皇后放置方式,但这将涉及超过 40 40 40 亿种排列组合,太慢了。
我们需要"更聪明地"暴力破解:
-
注意到我们可以直接生成一些排列,使得不会有两个皇后处于相同行或相同列,因此不会互相攻击。
-
由于不能有两个皇后在同一列,我们可以为每一列放置一个皇后。这样,每列就固定放一个皇后了。
-
剩下的就是确定每个皇后位于哪一行。我们可以通过生成 1 ⋯ 8 1 \cdots 8 1⋯8 的所有排列来完成,排列中的数字代表每列中皇后所处的行号。
例如,排列 [6, 0, 5, 1, 4, 3, 7, 2] 表示以下的皇后布局:
(接下来通常会展示一个 8 × 8 8×8 8×8 的棋盘图像,其中每列放置一个皇后,行号由该排列决定。)

cpp
#include <bits/stdc++.h>
using namespace std;
const int DIM = 8;
int main()
{
vector<vector<bool>> blocked(DIM, vector<bool>(DIM));
for (int r = 0; r < DIM; r++)
{
string row;
cin >> row;
for (int c = 0; c < DIM; c++)
{
// 如果该格子是 *,说明是禁止放置皇后的格子
blocked[r][c] = row[c] == '*';
}
}
vector<int> queens(DIM);
// 将初始排列设置为 0, 1, 2, ..., 7
iota(queens.begin(), queens.end(), 0); //iota 把一个范围内的元素填充为从某个起始值开始的连续整数序列
int valid_num = 0;
do
{
bool works = true;
// 检查是否有皇后放在了禁止格子上
for (int c = 0; c < DIM; c++)
{
if (blocked[queens[c]][c])
{
works = false;
break;
}
}
// 检查从左上到右下方向(↘)的所有主对角线是否有冲突
vector<bool> taken(DIM * 2 - 1);
for (int c = 0; c < DIM; c++)
{
// 使用 queens[c] + c 来标识对角线索引
if (taken[c + queens[c]])
{
works = false;
break;
}
taken[c + queens[c]] = true;
}
// 检查从右上到左下方向(↙)的所有副对角线是否有冲突
taken = vector<bool>(DIM * 2 - 1);
for (int c = 0; c < DIM; c++)
{
// queens[c] - c 可能为负数,因此加上 DIM - 1 来偏移
if (taken[queens[c] - c + DIM - 1])
{
works = false;
break;
}
taken[queens[c] - c + DIM - 1] = true;
}
// 如果当前排列满足所有条件,就计数加一
if (works)
{
valid_num++;
}
// 生成下一个排列(全排列)
} while (next_permutation(queens.begin(), queens.end()));
cout << valid_num << endl;
}