icpc中求解各种搜索问题的算法

惆怅客1232026-01-04 12:33

icpc中求解各种搜索问题的算法

搜索问题通常有 判定是否有解、找最优解、找所有解 这几种类型，换一个视觉看，有些搜索问题其实是 路径寻找、对抗搜索、精确覆盖、重复覆盖 之类的问题。

判定是否有解、找所有解 通常采用DFS，往往还伴随使用回溯法，有时候还可以做一些剪枝优化以及启发式搜索。当然，找所有解也可以采用BFS。

找最优解、路径寻找 问题通常采用BFS、双向BFS（Bi-directional BFS）、迭代加深搜索（IDDFS）、启发式搜索、 A ∗ A^* A∗搜索和 I D A ∗ IDA^* IDA∗搜索。部分求最优解的路径寻找问题可以建图跑最短路算法求解。

对抗搜索是一个 minimax 搜索过程，经常用 alpha-beta 剪枝策略。

精确覆盖、重复覆盖通常用 DLX 算法求解。

多数搜索问题看完题后就能很快选定求解算法框架，再从状态表示、状态压缩、剪枝策略、启发函数的角度做一下优化即可。但也有一些题目可能需要先对整体规则做模拟，再去总结归纳状态表示或者枚举的方法才能选定求解算法框架，甚至要分多个阶段采用不同的搜索策略实现过程模拟与求解。

枚举方式分析与状态表示

UVa12325/LA5703 Zombie's Treasure Chest

题意：你有一个体积为N的箱子和两种数量无限的宝物。宝物1的体积为S1，价值为V1；宝物2的体积为S2，价值为V2。输入均为32位带符号整数。你的任务是计算最多能装多大价值的宝物。例如，n=100，S1=V1=34，S2=5，V2=3，答案为86，方案是装两个宝物1，再装6个宝物2。每种宝物都必须拿非负整数个。

分析 ： 箱子实际装的宝物总体积大于 N − min ⁡ ( S 1 , S 2 ) N - \min(S1,S2) N−min(S1,S2)，因此枚举总体积的范围是区间 ( N − min ⁡ ( S 1 , S 2 ) , N ] (N - \min(S1,S2),N] (N−min(S1,S2),N]，枚举量为 min ⁡ ( S 1 , S 2 ) \min(S1,S2) min(S1,S2)。枚举一个宝物的数量，另外一个宝物的最大数量能自动算出，枚举量为 m i n ( ⌊ N S 1 ⌋ , ⌊ N S 2 ⌋ ) min(\left \lfloor \frac N {S1} \right \rfloor, \left \lfloor \frac N {S2} \right \rfloor) min(⌊S1N⌋,⌊S2N⌋)。因此 min ⁡ ( S 1 , S 2 ) < m i n ( ⌊ N S 1 ⌋ , ⌊ N S 2 ⌋ ) \min(S1,S2) < min(\left \lfloor \frac N {S1} \right \rfloor, \left \lfloor \frac N {S2} \right \rfloor) min(S1,S2)<min(⌊S1N⌋,⌊S2N⌋) 时枚举箱子实际装的宝物总体积；否则按照 m i n ( ⌊ N S 1 ⌋ , ⌊ N S 2 ⌋ ) min(\left \lfloor \frac N {S1} \right \rfloor, \left \lfloor \frac N {S2} \right \rfloor) min(⌊S1N⌋,⌊S2N⌋) 选取枚举一个宝物的数量。

UVa10603 Fill

题意 ：有装满水的6升的杯子、空的3升杯子和1升杯子，3个杯子中都没有刻度。在不使用其他道具的情况下，是否可以量出4升的水呢？方法如下图所示：(6,0,0)→(3,3,0)→(3,2,1)→(4,2,0)

注意：由于没有刻度，用杯子x给杯子y倒水时必须一直持续到把杯子y倒满或者把杯子x倒空，而不能中途停止。你的任务是解决一般性的问题：设3个杯子的容量分别为a, b, c，最初只有第3个杯子装满了c升水，其他两个杯子为空。最少需要倒多少升水才能让某一个杯子中的水有d升呢？如果无法做到恰好d升，就让某一个杯子里的水是d'升，其中d'<d并且尽量接近d。（1≤a,b,c,d≤200）。要求输出最少的倒水量和目标水量（d或者d'）。

分析 ： 直接枚举前两个杯子的水量，第3个杯子的水量也就知道了，状态数不会超过 201 2 = 40401 201^2=40401 2012=40401。抓住每次倒水必然有杯子被倒空或者倒满这一点，可以定义三维状态：记录倒空或者倒满的杯子编号（0、1、2）、是倒空还是倒满（0：空，1：满）以及其下一个杯子的水量（0~200）。那么总状态数才 3 × 2 × 201 = 1206 3\times 2\times201=1206 3×2×201=1206 。用Dijkstra求最短路解法即可。

过程模拟与多步搜索

UVa1491/LA5693 Compress the String

题意 ：丹正在和本玩游戏。本给了丹一个长字符串 S，丹需要将 S 压缩成一个由短字符串组成的列表：s[1]，s[2]，...，s[N]。S 只包含小写字母。每个 s[i] 可以包含小写字母和数字，但 s[i] 中只允许出现介于 i + 1 到 N（包含 N）之间的数字。例如，当 N = 4 时，s[2] 中允许出现的数字是 '3' 和 '4'。

为了将这样一个字符串列表解压缩成单个字符串，我们需要按相反的顺序（从 s[N] 到 s[1]）依次对每个字符串应用解压缩算法。字符串的解压缩算法很简单：只需将字符串中的每个数字替换为对应索引的解压缩字符串。也就是说，对于字符串中的数字 i，它将被替换为解压缩后的字符串 s[i]。因为我们按相反的顺序应用解压缩算法，所以在其他字符串中用数字 i 替换之前，s[i] 总是已经被解压缩了。当所有字符串都解压缩完毕后，s[1] 的解压缩结果就是最终结果。如果解压缩的结果是 S，我们就说 S 可以被压缩成这个字符串列表。

现在本决定了丹可以使用的短字符串数量（N），以及每个短字符串的长度限制。丹需要判断在给定的限制下，是否有可能将 S 压缩成 N 个短字符串。

分析：充分理解题意之后，用dfs+回溯法模拟整个过程即可。

UVa1063/LA3807 Marble Game

题意 ：滚球游戏由一个 n×n（2≤n≤4）网格棋盘和 m 个小球组成。棋盘上恰好有 m 个单元格里有洞。球和洞均编号为 1~m。滚球游戏的目标为把每个球滚到编号相同的洞中。单元格的 4 条边上可能会有墙，可以阻挡球的滚动（见后）。

每次可以把棋盘朝着上下左右 4 个方向之一微微抬起，然后所有球同时朝另一个方向滚动，直到碰到墙、洞或者另一个球。球在滚动的过程不能跳起（因而无法越过墙、其他球或者洞），也不能离开棋盘（整个棋盘的四周都有墙）。每个单元格恰好能容纳一个球。当球落入洞之后，洞将被填平，使得今后可以有其他球经过。入洞的球将无法出洞。

下图所示是一个滚球游戏及其解法。你的任务是解决任意一个 n×n 棋盘上的滚球游戏，找出移动次数最小的解，输出其长度。

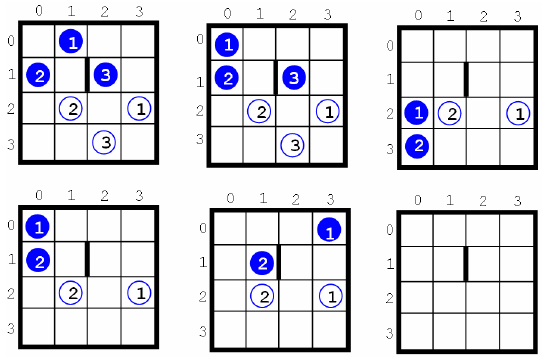
分析：本题直接bfs，模拟游戏过程直到找到解或者判定出无解即可。

UVa10639 Square Puzzle

题意：给出n个简单多边形和整数m (1≤m,n≤6)，多边形的每个顶点都是[0,m]内的整数，多边形的边只可能是水平、竖直或者对角线方向，每个多边形只能旋转但不能翻转。请判断这些多边形是否恰好能拼接成边长为m的正方形（每个多边形都要使用且拼接时不能重叠）。

分析 ：根据题目的数据规模，可以将正方形当成m×m的网格，则最终每个网格要么被一个多边形的某部分完全填充，要么被两个多边形各自填充一个三角形，dfs+回溯法可解。

将多边形内部也网格化，则多边形的每个网格形状是正方形或三角形。实际判断多边形填充网格的形状时需要计算点是否在多边形内，并判断填充网格后具体是三角形还是正方形。

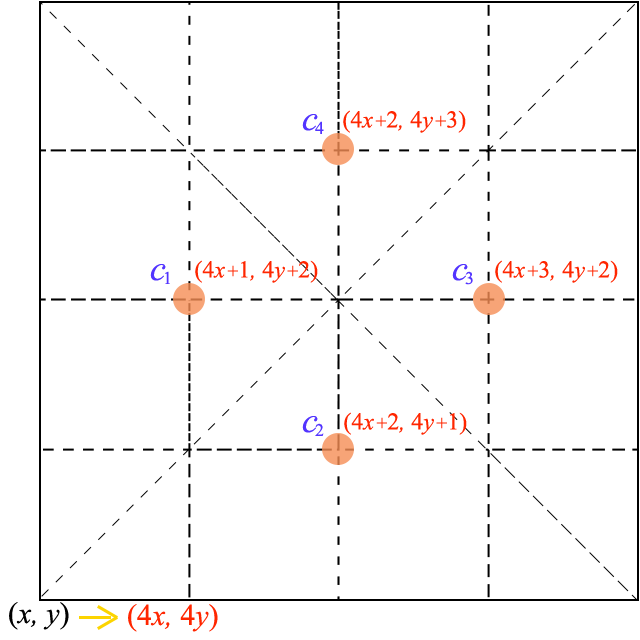
考虑网格网格的几个等分线交点c1、c2、c3、c4（见上图），计算它们在多边形内外的实际结果即可判定填充结果是正方形还是多边形：4个点都在多边形内则为正方形、C1与C2（或C3与C4、或C2与C3、或C1与C4）均在多边形内则为三角形。网格四等份后，c1、c2、c3、c4的坐标变成小数了，实际计算时可以将坐标值乘4（原多边形顶点坐标值也都乘4）来消除小数。

UVa1508/LA5842 Equipment

题意：一种武器装备按5个方面分别打分(0~10000)，若同时选择了多种装备，则每个方面的得分为这些装备此方面得分的最大值。给出n(1≤n≤10000)种装备的打分数值，求选择其中k(1≤k≤n)种装备时最大总得分。

分析：如果k≥5，则只需要对每方面得分从n个装备种找到最大值，求和即可。 如果k<5，其实也可以借鉴前一种的思路：只要把某几个方面的得分"捆绑"在一起，当成一个方面，将5个方面缩减成k个方面，用同样的方式可求。此时需要dfs枚举"捆绑"的所有可能，记录某个"捆绑"情况，可以用数组a[5]，a[i]=j表示第i(1≤i≤5)个方面最终"捆绑"到了第j(1≤j≤k,k<5)个方面。

UVa1448/LA4644 Hobby on Rails

题意 ：有一种轨道车玩具，h行w列矩形上的一个单元格即位一片轨道(2 ≤ h, w ≤ 6)，轨道一共分4种(见下图)，每片轨道可以90度倍数旋转。

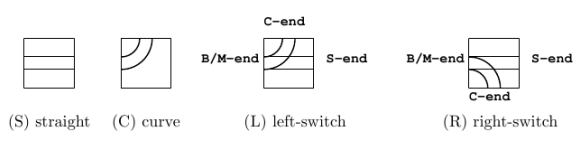
切换型轨道有直行/转弯两种状态。当玩具车从B/M端驶入时：如果此轨道为直行状态，则玩具车将从s端驶出，接下来此轨道切换为转弯状态；如果此轨道为转弯状态，则玩具车将从c端驶出，接下来此轨道切换为直行状态。当玩具车从S/C端驶入时，玩具车将从B/M端驶出并且此轨道状态不变。

切换型轨道的数量t满足：2 ≤ t ≤ 6。由于轨道可以旋转，要求合法旋转状态为： 每个切换型轨道的三端都直接或间接连接到了自己或其他切换型轨道。在合法旋转状态下，玩具车最终将沿着某个线路循环运动，可以求出此线路的周期T，它由(玩具车的初时位置, 玩具车的行驶方向, 所有切换型轨道的初时状态)三元组决定。

给定矩形上轨道方格的初时信息，求所有旋转后合法状态下的周期最大值。如果没有合法旋转状态，输出0。

分析：分多步搜索。

  • 先得到所有合法旋转状态，枚举每个切换型轨道可能的旋转状态(边界上的轨道状态可以检验一下)，再dfs拓展枚举他们实际需要延伸的周边轨道，验证要求是最终每个切换型轨道的三端都直接或间接连接到了自己或其他切换型轨道。
  • 每得到一个合法旋转状态：
    • 先计算好每一个切换型轨道从三端驶出并驶入到下一个切换型轨道的信息：步数，下一切换型轨道驶入的端。
    • 再枚举所有切换型轨道的初时状态，然后依次选择一个切换型轨道的某一端作为初时驶出点，dfs求周期T，并更新答案。

贪心、启发式搜索

UVa12130/LA3977 Summits

题意 ： 给定一个 h ∗ w h*w h∗w的地图（ 1 ≤ w , h ≤ 500 1\leq w,h\leq 500 1≤w,h≤500），每个位置有一个高度值，现在要求出这个图上的峰顶有多少个。峰顶是这样定义的：对于给定 d d d 值，一个高度为 h h h 的位置，如果它不经过不大于高度为 h − d h-d h−d 的位置就无法走到更高的山峰，那么它就是峰顶。

分析 ：如果数据规模小，对每一个点做dfs即可求解，但是题目交代的数据规模大，需要做优化，优化的思路是贪心加bfs：先将所有点按照高度递减排序，再依次遍历每个点做bfs。

具体来说，用数组 f [ w ∗ h ] f[w*h] f[w∗h] 记录每个点在给定d值条件下可以到达的最大高度（初始值全为负，代表未求解且未遍历到）。然后按高度递减排序后依次做dfs遍历，开始时计数cc=1，能到达的最大高度gx = g，初始点入队列，初始点（记其高度为g）在d值限定下可以经过的点v有以下情况：1、f[v] > gx, 说明初始点不是峰顶，gx = f[v]；2、f[v] < 0，则加入队列且赋值f[v] = g，并且若h[v] == g，则++cc。bfs结束时：若gx == g，说明本次找到cc个峰顶；否则本次未找到峰顶。

这里贪心的点在于：所有遍历到的点都是在最大下降高度<d的前提下进行的，将高度降序排列了，后遍历点经过已遍历点时所有遍历过的点必然满足高度限制，所以后遍历到的点走到已遍历的非峰顶的点时能判定出此轮高度不超过初始点的都不是峰顶。

分析一下时间复杂度：记 n = w ∗ h n=w*h n=w∗h，其实所有bfs做完仍然是O(n)时间复杂度，排序导致整体时间复杂度为 O ( n ∗ l o g n ) O(n*logn) O(n∗logn)。

UVa1302/LA2417 Gnome Tetravex

题意 ：有 n × n    ( 1 ≤ n ≤ 5 ) n\times n\;(1 \le n \le 5) n×n(1≤n≤5) 张正方形卡片，每张卡片分为上下左右四个三角形，三角形内各有一个 0~9 的数字，问能否把这些卡片排成 n\\times n 的方阵使得相邻卡片上相邻的三角形内数字相同。

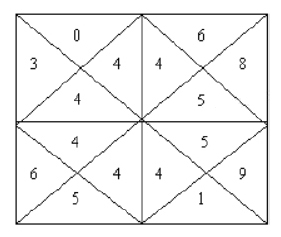
分析：将启发式搜索用于DFS优化。每张卡片分为上下左右四个三角形，其内各自包含一个数字，但是卡片要作为一个整体去摆放。不妨将其弱化使得摆放限制更宽松：将每张卡片裁剪成上下左右四个三角形，然后再去以三角形为单位进行摆放，这时候如果无解则原问题必然无解。因此可以用这个弱化的摆放限制作为启发函数 h：每次 DFS 搜索前，将尚未枚举到的那些卡片的上下左右四个三角形内数字按数值和方位分类统计，除了边界三角形外，其他三角形必须是数字相同的（上、下或者左、右）两两配对，也就是说剩下的卡片中不能配对的上下左右三角形数量不能大于剩下区域对应的上下左右边长，并且需要在统计时先将已摆放区域的下轮廓线上的三角形数字对应减掉。

UVa1499/LA5722 Gem And Prince

题意 ： 一个 n 行 m 列的矩阵一开始有 k 种不同的元素（元素值为1、2、...、k），可以选择任意一个至少包含 3 个元素的 8 连通块将其内元素消除，此时得分为消除元素数量的平方。某个元素被消除后，其上如果有元素，这些元素会下沉，且某列如果没有元素了，其右边的那些列会左移，如下图所示。

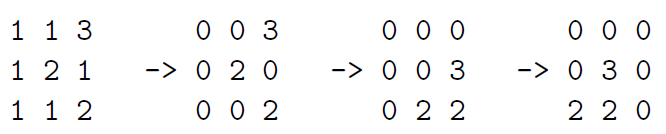
消除一次后得到新的矩阵，又可以继续在新的矩阵中选择任意一个至少包含 3 个元素的 8 连通块将其内元素消除，得分再增加本次消除元素数量的平方，注意数值为 0 的元素是已经消除了的，不能再被消除。

当没法再消除时，游戏结束。请找出初始矩阵进行游戏后的最大得分。

分析 ：启发式搜索，用A*算法即可AC。每次对当前矩阵找出所有至少包含 3 个元素的 8 连通块，依次枚举消除这些连通块后的新矩阵看启发函数值加当前消除路径下的累加得分是否超过答案，不超过答案则可以剪枝。

启发函数可以这样定：直接统计新矩阵内不同元素各自的数量，对大于 3 的那些数量取平方和。

对抗搜索

UVa10838 The Pawn Chess

题意 ：考虑如下的迷你版象棋：4×4 的棋盘上有一些黑兵和白兵。黑兵的目标是向下走到第四行，白兵的目标是向上走到第一行。如果一方无棋可走，则立刻输掉。

双方轮流走，白方先走。每次只能移动自己的一个兵，要么直着往前走一格（这个格子必须为空），要么斜着向前走一格，吃掉对方的棋子（不能吃掉己方的棋子，也不能斜着走到空格）。黑兵的"向前"指的是向下；白兵的"向前"指的是向上。

假设双方均采用最优策略，即如果能赢，则应该赢得尽量快；如果必须输，则应该输得尽量慢。

每组输入恰好包含4 行4 列，其中p 为黑兵，P 为白兵，'.'为空格。输入保证双方都至少有一种走法。

分析：不能很直观地用 alpha-beta 剪枝，按照极大极小过程处理即可。

cpp 复制代码 
#include <iostream>
using namespace std;

int minimax(unsigned int s, int p) {
    int a = 0, b = 16;
    for (int i=0, k=0; i<4; ++i) for(int j=0; j<4; ++j, k += 2) {
        int x = s>>k & 3;
        if (x == p) {
            if (p && i > 0) {
                if ((s>>k-8 & 3) == 2) {
                    if (i == 1) return 1;
                    int v = minimax(s + (255<<k-8), 0);
                    v & 1 ? a = max(a, v+1) : b = min(b, v+1);
                }
                if (j>0 && (s>>k-10 & 3) == 0) {
                    if (i == 1) return 1;
                    int v = minimax(s + (1025<<k-10), 0);
                    v & 1 ? a = max(a, v+1) : b = min(b, v+1);
                }
                if (j<3 && (s>>k-6 & 3) == 0) {
                    if (i == 1) return 1;
                    int v = minimax(s + (65<<k-6), 0);
                    v & 1 ? a = max(a, v+1) : b = min(b, v+1);
                }
            } else if (!p && i<3) {
                if ((s>>k+8 & 3) == 2) {
                    if (i == 2) return 1;
                    int v = minimax(s - (510<<k), 1);
                    v & 1 ? a = max(a, v+1) : b = min(b, v+1);
                }
                if (j>0 && (s>>k+6 & 3) == 1) {
                    if (i == 2) return 1;
                    int v = minimax(s - (62<<k), 1);
                    v & 1 ? a = max(a, v+1) : b = min(b, v+1);
                }
                if (j<3 && (s>>k+10 & 3) == 1) {
                    if (i == 2) return 1;
                    int v = minimax(s - (1022<<k), 1);
                    v & 1 ? a = max(a, v+1) : b = min(b, v+1);
                }
            }
        }
    }
    return b&1 ? b : a;
}

void solve() {
    unsigned int s = 0;
    for (int i=0, k=0; i<4; ++i) for(int j=0; j<4; ++j, k += 2) {
        char ch; cin >> ch;
        s |= (ch == 'P' ? 1 : (ch == 'p' ? 0 : 2)) << k;
    }
    int v = minimax(s, 1);
    v&1 ? cout << "white (" << v << ')' << endl : cout << "black (" << v << ')' << endl;
}

int main() {
    int t; cin >> t;
    while (t--) solve();
    return 0;
}

UVa12180/LA4300 The Game

题意 ： 这是一个双人游戏。两个人面对面坐下，每个人正前方有m（1≤m≤4）个杯子，右手边是一只大碗。不难发现，一共有2(m+1)个杯子和碗，它们摆成一个圈。游戏开始时，这些杯子和碗里有一些石子，加起来不超过15 个。每个游戏者碗里的石子数代表他的得分。

游戏规则如下：双方轮流操作，每次游戏者可以选择一个他自己的有石子的杯子，按照逆时针顺序把这些石子放到该杯子的各个相邻杯子/碗中（包含该杯子自己），每次放一个石子。

如下图左所示的局面中，如果下方的游戏者选择杯子A，则需要把杯子A 里的4个石子分到杯子B， C，自己的碗和杯子 a 里。这样比分从3:4 变成了4:4。

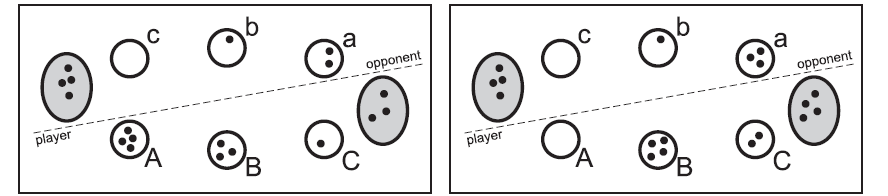
有 3 种特殊情况。

第一，如果最后一个石子放在了自己碗里，需要再操作一次。如果最后一个石子又放在了自己的碗里，还需要再操作一次，次数不限，直到不满足这个条件为止。

第二，如果最后一个石子放到了对方的杯子里，可以把这个杯子和自己对应的杯子交换（也可以不交换，A 和 a 对应，B 和 b 对应...）。如果自己对应的杯子为空，则不能交换。双方在整个游戏中各有三次交换机会，而且当一个杯子被交换过以后，接下来的4 轮中不能再次被交换（一次连续操作称为一轮）。考虑如下的操作序列：P0, O1, O2, O3, P4, O5, P6, O7，其中Pi是己方的操作，Oj 是对方的操作。如果P0 中交换了某两个杯子，接下来的四轮（第一轮是O1, O2, O3，第二轮是P4，第三轮是O5，第四轮是P6）都不能再交换这两个杯子，但O7 中可以再次交换。

第三，如果最后一个石子放在己方的杯子里，并且放之前这个杯子是空的，并且这个杯子正对的杯子（上图中A 正对着c，B 正对b，C 正对a）在放石子之后非空，这两个杯子中的所有石头都将移到自己的碗里。注意，这种情况不会引起连锁反应（即接下来轮到对方操作）。

所有杯子都为空时游戏结束。如果轮到某一方操作时他的所有杯子均为空，则下一轮仍该对方操作（但对于交换规则来说，"无法操作"也将算作一轮）；但只要有非空杯子，游戏者必须操作，而不能跳过这一轮。

假设双方都是足够聪明的，己方得分与对手的得分之差最大是多少？（己方得分大时，结果越大越好，己方得分小时，结果越小越好）。

分析：典型的极大极小搜索，上 alpha-beta 剪枝即可。主要难点在于对题意的仔细理解，笔者的翻译已经很详细了，参照翻译去做比看原英文题面省事。

UVa1495/LA5715 Three Kingdom Chess

题意 ：三国时期诸葛亮和周瑜经常在一起玩一种双人对战棋类游戏，二人在 N 行 M 列的棋盘上轮流操作 K 次，总是诸葛亮先手。一共有三种类棋子：步兵、骑兵、弓箭手，他们各自的攻击范围见下图。每类棋子可以向上下左右移动一格，可以移动多次，但是在一轮操作下其移动动步数有上限。初始时双方各自的棋子都在棋盘格的某个位置且一个格子上最多只有一个棋子。棋盘的格子也有分类：平原、山、湖。所有棋子都不能走进或穿过湖并且骑兵还不能走进或穿过山，棋子可以经过友方棋子所在的位置但不能停在此处，棋子不能到达或穿过敌方棋子所在处。

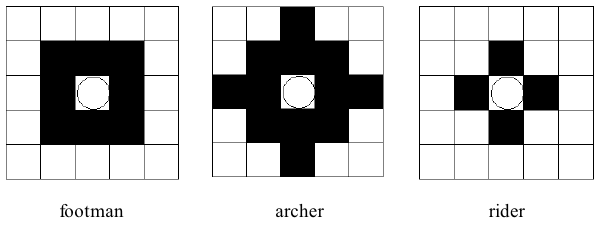
棋手每轮操作时可以选定己方的一个棋子（假设这种棋子的单轮移动动步数的限制为 q）移动 [ 0 , q ] [0,q] [0,q] 步，再选一个其攻击范围内的敌方棋子进行攻击。棋子受攻击后，其体力将减弱，减弱量为攻击者的体力值 S 乘以攻击系数 F 再向下取整，即 ⌊ S × F ⌋ \lfloor S \times F \rfloor ⌊S×F⌋。当一个棋子体力值小于等于 0 后，它将阵亡消失。当游戏进行了 K 轮或者某一方的棋子全部阵亡，游戏结束计算得分，得分计算方式为诸葛亮的所有棋子体力之和减去周瑜的所有棋子体力之和。攻击系数 F 是这样的：步兵攻击弓箭手、弓箭手攻击骑兵、骑兵攻击步兵时，系数都是 2；步兵攻击步兵、弓箭手攻击弓箭手、骑兵攻击骑兵时，系数都是 1；步兵攻击骑兵、骑兵攻击弓箭手、弓箭手攻击步兵时，系数都是 0.5。

诸葛亮和周瑜都非常聪明，他们都会采用最优策略使得自己操作后最终得分最优，问游戏结束时诸葛亮的得分为多少。

分析：极大极小搜索，上 alpha-beta 剪枝。

有一个坑就是"棋手每轮操作时可以选定己方的一个棋子（假设这种棋子的单轮移动动步数的限制为 q）移动 [ 0 , q ] [0,q] [0,q] 步，再选一个其攻击范围内的敌方棋子进行攻击。"这里，原英文题面如下：

In each turn, the player can move one of his soldiers to a destination and then let it attack one of the opponent's soldiers.

仔细推敲这里的"可以"，考虑到兵法常说按兵不动 ，这里的"可以"也意味着某轮操作不选任何兵，不动也不攻击，也可以选一个兵只移动而不攻击（可以想象此兵很弱，但他能跑到敌方无论如何移动都无法攻击到的地方，他不死那么对最终得分还是有贡献）。下面这条数据就是按兵不动 的例子：

3 2 10

0 1

1 2

0 0

3 10 8 7

3 1 0 6555 1

1 2 1 6616 1

1 1 1 1364 1

0 0 0

这个按兵不动的策略需要在状态拓展时去重，否则大量相同的状态容易引发超时，并且移动时可以限制不能回头（走回上一次的位置）。

精确覆盖、重复覆盖

UVa1309/LA2659 Sudoku

数独是舞蹈链算法（DLX）求解精确覆盖问题的经典题目。

cpp 复制代码 
#include <iostream>
#include <cstring>
using namespace std;

#define maxNode 17409   //16384+1025
#define maxC 1025
#define maxR 4096

short n=1024, sz, ansd, ans[maxR], S[maxC], H[maxR];
short row[maxNode], col[maxNode], L[maxNode], R[maxNode], U[maxNode], D[maxNode];

void init() {
    for (short i=0; i<=n; ++i) {
        S[i] = 0; U[i] = D[i] = i; L[i] = i-1; R[i] = i+1;
    }
    R[n] = 0; L[0] = n; sz = n+1;
    memset(H, 0, sizeof(H));
}

void link(short r, short c) {
    D[U[c]]=sz; U[sz]=U[c]; D[sz]=c; U[c]=sz;
    if(!H[r]) H[r]=L[sz]=R[sz]=sz;
    else {
        L[sz]=L[H[r]]; R[L[H[r]]]=sz;
        R[sz]=H[r]; L[H[r]]=sz;
    }
    row[sz] = r; col[sz]=c; ++ sz; ++ S[c];
}

void remove(short c) {
    L[R[c]] = L[c]; R[L[c]] = R[c];
    for (short i=D[c]; i!=c; i=D[i])
        for (short j=R[i]; j!=i; j=R[j]) {
            U[D[j]] = U[j]; D[U[j]] = D[j]; --S[col[j]];
        }
}

void restore(short c) {
    for (short i=U[c]; i!=c; i=U[i])
        for(short j=L[i]; j!=i; j=L[j]) {
            U[D[j]] = D[U[j]] = j; ++S[col[j]];
        }
    L[R[c]] = c; R[L[c]] = c;
}

bool dfs(short d=0) {
    if (!R[0]) {
        ansd = d;
        return true;
    }
    short c = R[0];
    for (short i=R[0]; i!=0; i=R[i])
        if (S[i] < S[c]) c = i;
    remove(c);
    for (short i=D[c]; i!=c; i=D[i]) {
        ans[d] = row[i];
        for (short j=R[i]; j!=i; j=R[j]) remove(col[j]);
        if (dfs(d+1)) return true;
        for (short j=L[i]; j!=i; j=L[j]) restore(col[j]);
    }
    restore(c);
    return false;
}

short encode(short a, short b, short c) {
    return a<<8 | b<<4 | c;
}

void decode(short code, short& a, short& b, short& c) {
    a = code; c = a&15; a>>=4; b = a&15; a>>=4;
}

int main() {
    char sudoku[16][17]; int k=0;
    while (!cin.eof()) {
        for (short i=0; i<16; ++i) cin >> sudoku[i];
        if (k++) cout << endl;
        init();
        for (short r=0; r<16; ++r)
            for (short c=0; c<16; ++c)
                for (short v=0; v<16; ++v)
                    if (sudoku[r][c] == '-' || sudoku[r][c] == 'A'+v) {
                        short row = encode(r, c, v);
                        link(row, 1+encode(0, r, c));
                        link(row, 1+encode(1, r, v));
                        link(row, 1+encode(2, c, v));
                        link(row, 1+encode(3, ((r>>2)<<2)+(c>>2), v));
                    }
        dfs();
        for (short i=0; i<ansd; ++i) {
            short r, c, v; decode(ans[i], r, c, v);
            sudoku[r][c] = 'A'+v;
        }
        for (short i=0; i<16; ++i)
            cout << sudoku[i] << endl;
    }
    return 0;
}

UVa1603/LA2328 Square Destroyer

题意 ：有一个火柴棍组成的正方形网格，每条边有n根火柴，共2n(n+1)根。从上到下、从左到右给各个火柴编号，如图7-24（a）所示。现在拿走一些火柴，问在剩下的火柴中，至少还要拿走多少根火柴才能破坏所有正方形？如下图（b）中，拿掉3根火柴就可以破坏掉仅有的5个正方形。

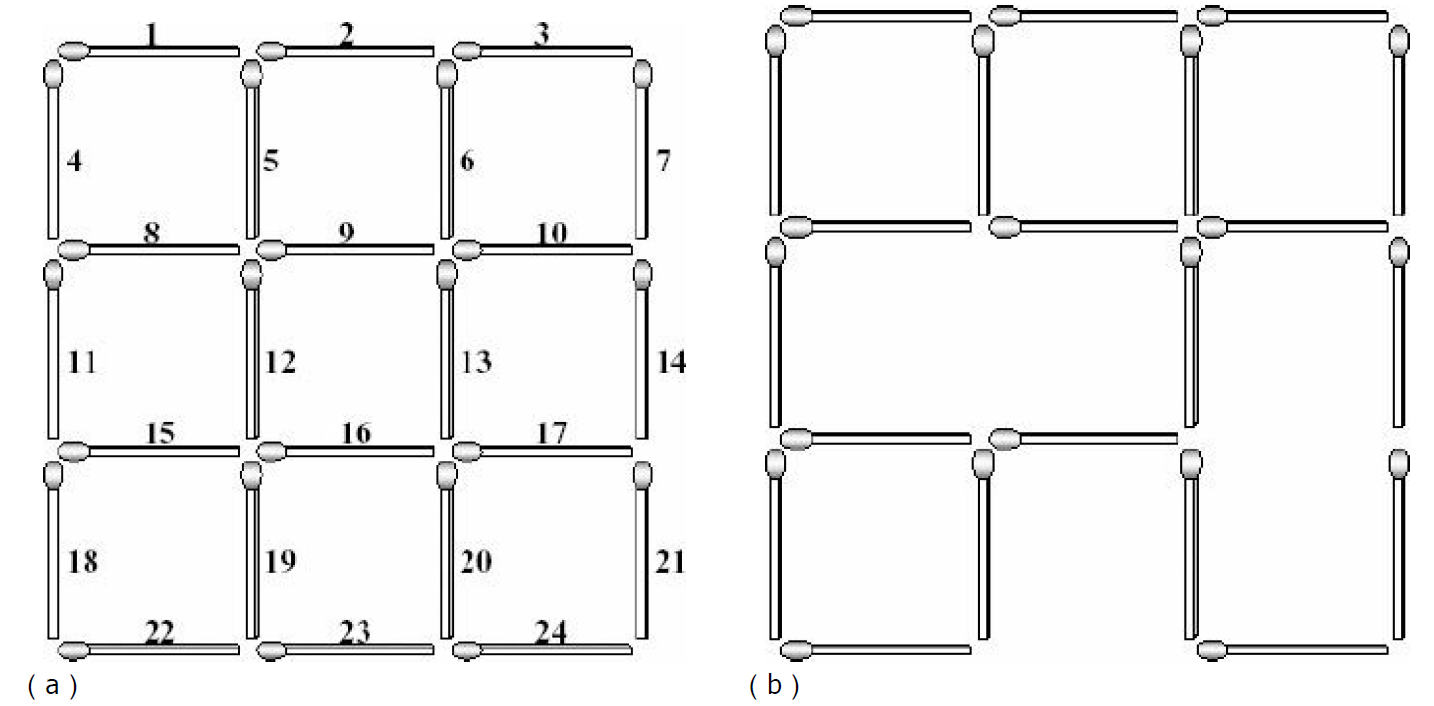
分析：不难想到用迭代加深搜索作为主算法框架。搜索对象有两种：（1）每次考虑一个没有被破坏的正方形，在边界上找一根火柴拿掉；（2）每次找一个至少能破坏一个正方形的火柴，然后拿掉。两种方法各有不同的优化方法：

搜索对象是正方形。应先考虑小正方形，再考虑大正方形，因为破坏完小正方形之后，很多大正方形已经被破坏了，但是反过来却不一定。还可以加入最优性剪枝，即把每个正方形看成一个顶点，有公共火柴的正方形连一条边，则每个连通分量至少要拿走一根火柴。

搜索对象是火柴。应先搜索能破坏尽量多正方形的火柴。这需要计算出待考虑的每根火柴可以破坏掉多少个正方形，从大到小排序为d[1], d[2], d[3],......当d[1]=1时即可停止搜索，因为此时可以直接计算出还需要的火柴个数（想一想，为什么）。这个d数组也可以用于最优性剪枝，找到最小的i，使得d[1]+d[2]+...+d[i]≥k（其中k为还剩的正方形个数），则至少还要i根火柴。

作为典型的重复覆盖问题，本题可以用DLX算法解决。重复覆盖DLX算法可以用精确覆盖作为启发函数去优化。

BFS、双向BFS（Bi-directional BFS）

UVa12418 Game of 999

题意 ：注意，本题选材自 NDS 经典悬疑类密室逃脱游戏《9 小时9 人9 扇门》。本题不含任何剧透，只包含一些基本游戏规则的描述。这些规则和原游戏中的有所出入，请玩过游戏的读者仔细阅读题目。

迷宫中有n（n≤10）个房间和m（m≤10）个连接它们的走廊。一些走廊的中部有一扇门，门上有一个1~9 的数字。走廊都是单向的，因此这些门也只能从一边打开。编号为 1 ∼ 9 1\sim9 1∼9 的 9 个人一开始在房间 1 中，目标是从房间 n 中的出口逃脱。游戏规则如下。

  • 每扇门只能开一次。一旦有人通过，门将永远锁住。
  • 每扇门只能由 3~5 个人打开，而且这些人编号之和的数字根必须等于门上的数字。所谓数字根，即反复把各个数字加起来，直至得到一个一位数为止。例如，3，5，6，8 可以打开 4 号门，因为3+5+6+8=22，它的数字根为2+2=4。打开门的所有人都必须通过它，并且其他人都不能通过这扇门。

你的任务是编写一个自动求解器，使得尽量多的人能够逃脱，在此前提下输出所有可能的逃脱组合。注意，每个房间可以多次进入（包括房间n），但一旦逃出迷宫，就不能再回到迷宫了。可以有多条走廊连接同一对房间，但不会有走廊的起点和终点是同一个房间。

分析 ：可以先预处理数字根为 1 ∼ 9 1\sim9 1∼9 各自包含的各种集合，预先打表存储，那么对每组数据求解时枚举到一个走廊时，一定是在对应数字根集合里面挑选起点内人员的子集，可以发现每个有门走廊的子集枚举量才37或38个。具体求解用 BFS，采用集合对状态判重即可通过了。

UVa1008/LA2240 A Vexing Problem

题意 ：Vexed 游戏是James McCombe 发明的一种类似俄罗斯方块的游戏。在游戏中，一面木头墙上放置了一些标有字母的白色石块。

如果某个石块的左边（或者右边）是空的，那么该石块可以向左（或者向右）移动一步，木头墙永远不能移动，悬空的石块会自动下掉。每个石块都有一个标记，两个或更多具有相同标记的石块相碰时会形成石块群，石块群会自动消失。如果同时形成了多个石块群，那么它们会一起同时消失。石块群消失后，悬空的石块同样会自动下掉，下掉后石块群同样会消失......如此循环，直到石块不再变化为止。游戏的目标就是让所有的石块消失。

如下图（a）到（h）所示就是一个从初始状态到石块全部消失的游戏过程：首先上面的"Y"石块左移，这样两个"Y"石块形成石块群自动消失；然后上面的"X"石块右移，右移后下掉，这样两个"X"石块也形成石块群自动消失。

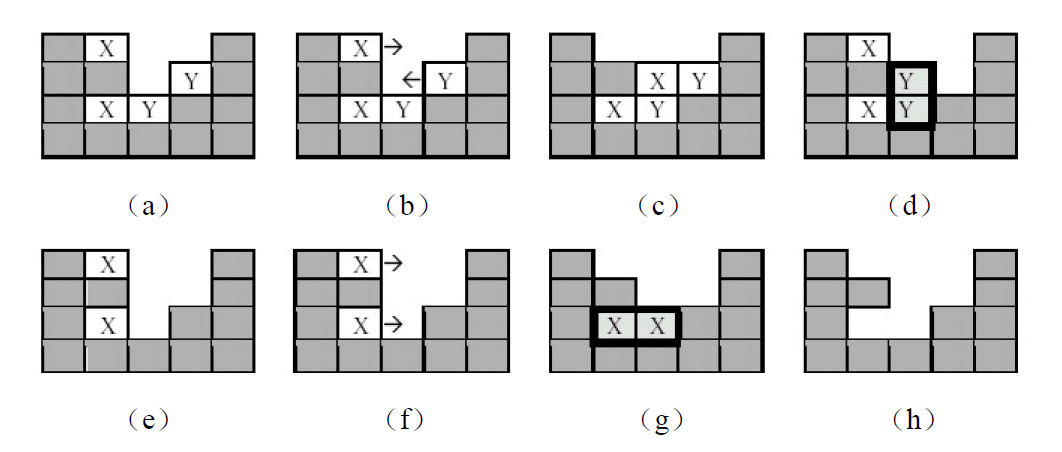
下图所示是另一个游戏过程：首先最左边的"Z"右移（图a），形成"X"、"Z"石块群（图b）；石块群消失后，又形成"Y"、"Z"、"X"石块群；石块群消失后，最后形成"X"石块群，"X"石块群消失后游戏结束。

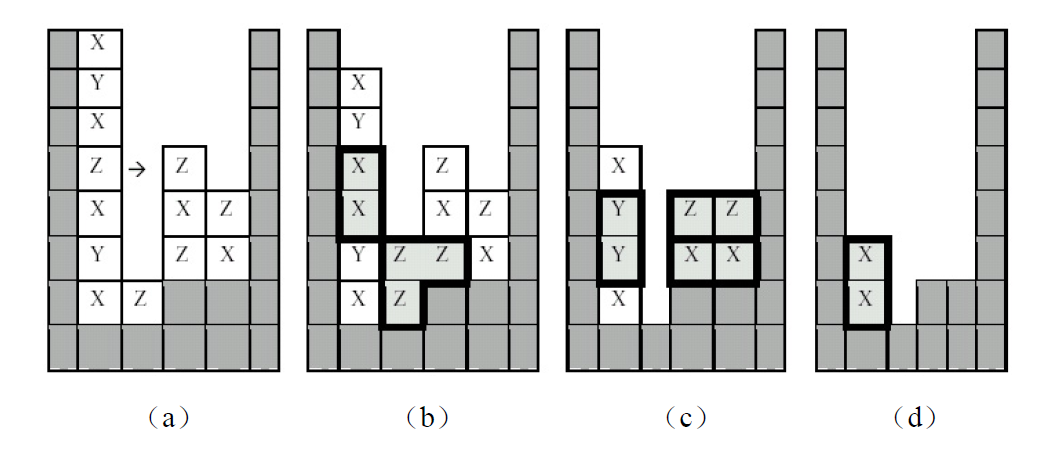
写一个程序，任意给出一个游戏，给出步数最少的解。行数 R 和列数 C 满足 4≤R，C≤9，第一列、最后一列和最后一行保证为墙（#）输入保证存在一个不超过11 步的解。

分析：本题限时30s，暴力法能过，直接 BFS 并用集合对状态判重即可。

UVa1353/LA3402 Organize Your Train

题意 ：东京有一个老旧的火车站，含有若干条只在夜间运行的东西向火车线路，每天的运行结束后，第二天线路上火车需求有变，需要把这些火车的车厢打散重新组装。某条火车线路线路的两端可能有一些交换线连接到其他火车线路，可以把它的火车车厢从某个位置断开再沿着交换线将断开部分或者整个火车移动到连接到的火车线路上并组装出新的火车。

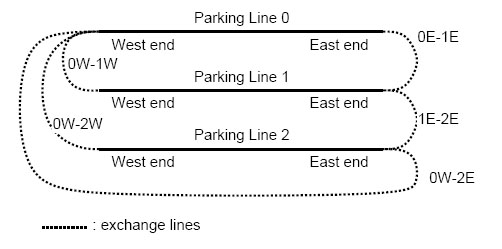
用a-z这些小写字母组成的字符串表示火车的每个车厢，相同的小写字母代表规格相同的车厢，不同的小写字母代表规格不同的车厢。给定某晚运行结束时各个火车线路上火车的字符串表示，以及第二天晚上各个火车线路上需要的火车的字符串表示，求最少的组装次数。下图是一个移动并组装的示例。

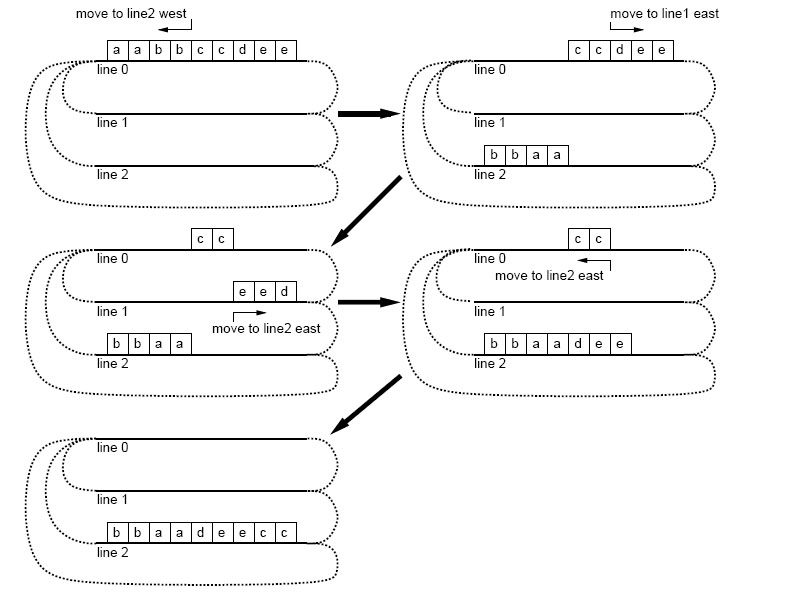
分析 ：本题似乎没法用启发式搜索，那么在要求最小解的情况下，用 BFS 合适一些。根据 x ≤ 4 x≤4 x≤4 且所有火车的车厢总数不超过 10 这个限制，从一个状态拓展出新状态的最大总数为 4 ∗ 3 ∗ 4 ∗ 10 = 240 4*3*4*10=240 4∗3∗4∗10=240，那么在拓展 6 层的话状态数可能会到 10 12 ∼ 10 14 10^{12}\sim 10^{14} 1012∼1014 数量级，会超时。

如果拓展 3 层的话状态数则在 10 7 10^7 107 内，这是可以接受的，因此想到双向 BFS 做法。先从起始状态 BFS 拓展3层，看这些状态中是否会出现目标状态，出现则直接找到了答案。若未出现答案，再从目标状态 BFS 拓展3层，当拓展状态在起始状态 BFS 拓展出来的结果中时则找到了答案。

各种剪枝

UVa11211 Digital Logic

题意 ：给你一些 2 输入 1 输出的逻辑门，你的任务是设计一个 4 输入 4 输出的数字电路。每一个逻辑门由 3 个 0-1 整数 Y00, Y01 和 Y11 描述。代表输入分别为 0，1，2 个 1 时的输出。注意所有的逻辑门都是对称的，所以当有一个输入被设置为 1 时，不管是哪一个输入门，输出的结果都相同。任何一个逻辑门的输入端都是另外一个逻辑门的输出端或者 4 个源输入端之一。由于当任何一个输入被悬挂时输出结果将不可预料，所以务必保证一个逻辑门的输出将不会再次变为其输入，不管是直接的还是间接的（换句话说，逻辑电路将不包含环路），如下图所示。

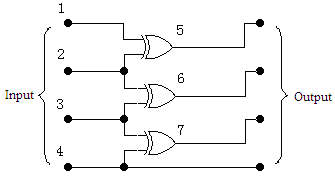
为了让设计更加简单，你需要使用尽可能少的逻辑门。题目保证所有输入数据都可以用最多 6 个逻辑门实现。

分析：基本框架是 BFS 并用集合对状态判重。主要难点在于状态设计以及状态拓展时的各种剪枝。先来看一下状态，必然要存每一个使用了的逻辑门种类、两个输入端口（输出端口可以暗含在状态中：从 0 开始编号的第 i 个实际使用的逻辑门其输出端口是 i+5），其他服务于剪枝的必要信息也可能会存入状态中。

怎么知道一个状态是结束状态呢？即此状态的所有输出中选出 4 个进行排列组合恰好能形成输入指定的 Ypqrs 的形式。选 4 个还要排列组合检验能否形成输入指定的 Ypqrs 的形式，那么代价在 A 14 4 = 24024 A^4_{14} = 24024 A144=24024，每次为了判断状态是否是结束状态就要花 20000 次枚举的话显然超时。可以想到对各个端口的输出和输入指定的最终 16 个输出进行转化，由于最终输出一定来自 4 个端口 a，b，c，d（可以有重复使用的端口），可以将最终 16 个输出按照端口转存成 4 个 16 位的二进制数（每一位依次代表输入是 0 ∼ 15 0\sim15 0∼15 时此端口输出的是 0 还是 1），这个转换顺便分析出了重复端口（两个相同的16 位的二进制即是重复的）。那么状态里面也需要用一个 16 位的二进制数存每个逻辑门的输出，再判断其是否是结束状态就很简单了：已经知道转移前状态得到了几个需要的输出，只需再看转移后新加的逻辑门是否增加了需要的输出，这需要将已经得到了几个输出也存入状态中。

几个剪枝：

  • 当前已经使用了 x 个逻辑门，由于"题目保证所有输入数据都可以用最多 6 个逻辑门实现 "，那么此后做状态拓展时最多能新得到 6-x 个需要的输出，也就是说如果当前状态已经得到 c 个（不同的）需要的输出，实际需要的输出去重后数量是 cc ，那么 c + 6 − x < c c c+6-x < cc c+6−x<cc 时可以剪枝。
  • 如果尝试新添加一个逻辑门，其输出在旧的端口中已经存在，那么不需要添加它，可以剪枝。
  • 任何状态，其未作为其他端口输入又不是最终需要的输出的逻辑门数量不超过 3 (虽然实际可以超过3，但是加这一个限制能减小枚举量并且不会错过最优解)，并且当已经使用了 5 个逻辑门时不超过 2， 已经使用了 6 个逻辑门时则应该为 0。
  • 任何状态，其未作为其他端口输入又不是最终需要的输出的那些逻辑门种类编号如果大于最新加入的逻辑门种类编号，则可以忽略此状态，这个剪枝的作用也是减小枚举量并且不会错过最优解。
  • 任何状态，如果其未作为其他端口输入又不是最终需要的输出的逻辑门数量为 3，那么进行状态拓展一定是从这些逻辑门中选两个或者选一个且从其他类型的旧逻辑门中再选一个作为新添加的逻辑门的输入端口。

I D A ∗ IDA^* IDA∗

UVa1063/LA3807 The Rotation Game

题意 ：如下图所示形状的棋盘上分别有8个1、2、3，要往A～H方向旋转棋盘，使中间8个方格数字相同。图（a）进行A操作后变为图（b），再进行C操作后变为图（c），这正是一个目标状态（因为中间8个方格数字相同）。要求旋转次数最少。如果有多解，操作序列的字典序应尽量小。

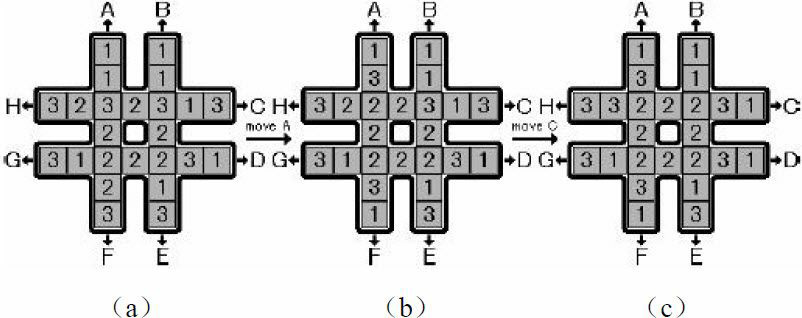
分析：《算法竞赛入门经典》题解：

本题是一个典型的状态空间搜索问题，可惜如果直接套用八数码问题的框架会超时。为什么？学完第10章的组合计数部分后会知道：8个1、8个2、8个3的全排列个数为24!/(8!*8!*8!)=9465511770。换句话说，最坏情况下最多要处理这么多结点！

解决方法很巧妙：本题要求的是中间8个数字相同，即8个1或者8个2或者8个3。因此可以分3次求解。当目标是"中间8个数字都是1"时，2和3就没有区别了（都是"非1"），因此状态总数变成了8个1，16个"非1"的全排列个数，24!/(8!*16!)=735471，在可以接受的范围内了。

非常好的状态空间分析思路，按这个思路写BFS，虽然较慢但能通过。用迭代加深搜索IDDFS会快一些，最优的方法还是 I D A ∗ IDA^* IDA∗，其启发式函数可以这样定：当前操作完成后，统计中间8个数字1、2、3数量的最大值x，则至少还需要8-x步操作。 I D A ∗ IDA^* IDA∗ 做法其实不需要进行状态空间分析，也就不用分中间8个数字都是1或者2或者3三类情况了。

UVa11212 Editing a Book

题意 ：你有一篇由n（2≤n≤9）个自然段组成的文章，希望将它们排列成1, 2,..., n。可以用Ctrl+X（剪切）和Ctrl+V（粘贴）快捷键来完成任务。每次可以剪切一段连续的自然段，粘贴时按照顺序粘贴。注意，剪贴板只有一个，所以不能连续剪切两次，只能剪切和粘贴交替。

例如，为了将{2,4,1,5,3,6}变为升序，可以剪切1将其放到2前，然后剪切3将其放到4前。再如，对于排列{3,4,5,1,2}，只需一次剪切和一次粘贴即可------将{3,4,5}放在{1,2}后，或者将{1,2}放在{3,4,5}前。

分析：《入门经典》题解如下：

本题可以用 I D A ∗ IDA^* IDA∗ 算法求解。不难发现n≤9时最多只需要8步，因此深度上限为8。 I D A ∗ IDA^* IDA∗ 的关键在于启发函数。考虑后继不正确的数字个数h，可以证明每次剪切时h最多减少3，因此当3d+h>3maxd时可以剪枝，其中d为当前深度，maxd为深度限制。

如何证明每次剪切时h最多减少3呢？如下图所示，因为最多只有3个数字的后继数字发生了改变（即图中的a, b, c），h自然最多减少3。

题解还说了3个加速策略，但需要自辩真伪，实际上有两个加速策略可用：

  • 永远不要"破坏"一个已经连续排列的数字片段。例如，不能把1 2 3 4中的2 3剪切出来。
  • 假设剪切片段的第一个数字为a，最后一个数字为b，要么把这个片段粘贴到a-1的下一个位置，要么粘贴到b+1的前一个位置。
      a-1的下一个位置和b+1的前一个位置都在剪切片段内部时只需要根据不"破坏"一个已经连续排列的数字片段原则选取粘贴点。

UVa1374/LA3621 Power Calculus

题意 ：输入正整数 n（1≤n≤1000），问最少需要几次乘除法可以从 x x x得到 x n x^n xn？例如， x 31 x^{31} x31需要 6 次： x 2 = x × x , x 4 = x 2 × x 2 , x 8 = x 4 × x 4 , x 16 = x 8 × x 8 , x 32 = x 16 × x 16 , x 31 = x 32 ÷ x x^2 = x×x, x^4 = x^2×x^2, x^8 = x^4×x^4, x^{16} = x^8×x^8, x^{32} = x^{16}×x^{16}, x^{31} = x^{32}÷x x2=x×x,x4=x2×x2,x8=x4×x4,x16=x8×x8,x32=x16×x16,x31=x32÷x。计算过程中x的指数应当总是正整数（如 x − 3 = x / x 4 x^{-3}=x/x^4 x−3=x/x4是不允许的）。

分析 ：用 I D A ∗ IDA^* IDA∗ 来做，基于贪心来构造启发函数：在当前计算出的指数序列的最大值为 x，已经计算了 s 步，最多计算 d 步的情况下，如果 x × 2 d − s < n x\times 2^{d-s} < n x×2d−s<n，则必然无法得到 n，剪枝。

还有如下优化策略：

  • 每次总是使用上一步得出的数进行加减操作（只需再从整个序列枚举出另外一个数）。
  • 超过 n 的数最多只需要一个。
  • 先考虑加法再考虑减法。

UVa1041/LA3272 cNteSahruPfefrlefe

题意 ：你有一副普通的扑克牌，叠成一摞放在桌子上。52 张牌从顶部到底部编号为0~51。理想情况下，如果把这些牌均分成上下两部分以后交叉洗牌，结果将是（仍为从顶部到底部排列）：26, 0, 27, 1, 28, 2, 29, 3, 30, 4, 31, 5, 32, 6, ..., 51, 25。

你按照这样的方法洗了若干次牌（洗牌次数未知但保证为1~10）。虽然你已经非常小心了，但人无完人，你仍有可能在洗牌后意外的交换两张相邻的牌（假定每次洗牌最多只在一个地方犯错），比如洗成：26, 0, 27, 1, 2, 28, 29, 3, 30, 4, 31, 5, 32, 6, ..., 51, 25。

给定洗牌后的结果，问最少犯了多少个错？如果有多组解，输出字典序最小的（只考虑洗牌出错的位置）。

分析 ：先分析一下单次洗牌出错对后续的影响，如果将 a、b 交换了，此后洗牌只要不再犯错，总是原本是 a 的地方出现 b，是 b 的地方出现 a，从图论的角度这构成一个环 a → b → a a\to b\to a a→b→a。如果有多次洗牌出错，同样在最后一次犯错之后，形成若干环，可能有多个环并且环长度可能大于 2。

如果环长度都为 2，可以直接搜索得出结果（枚举前 i 次洗牌都不出错的序列，看什么时候 a 和 b 相邻了），结果是唯一确定的。但是环长如果超过 2，由于结果不唯一，输出又要字典序，不好直接搜索了。

可以上 I D A ∗ IDA^* IDA∗，启发函数是这样的：将当前牌面序列直接按不犯错方式洗牌到预定次数后，计算最终和目标序列不同的牌数量 c，那么此后至少还要犯 ⌈ c 2 ⌉ \lceil \frac c 2 \rceil ⌈2c⌉ 次错误（因为长度为 n 的环对应犯错 n-1 次，那么环长度都为 2 时犯错次数才最小）。

UVa1505/LA5835 Flood-it!

题意 ： N × N N\times N N×N 网格的每个格子有一个 0 ∼ 5 0\sim 5 0∼5 的整数，数值相同且含公共边的相邻格子算同一个连通块。

在网格上的游戏这样进行：

  • 所有格子数值相同时，结束
  • 否则，将左上角所在连通块改成 0 ∼ 5 0\sim 5 0∼5 的新数值，数值修改后可能引起左上角所在连通块内的格子变多。每修改一次左上角所在连通块，操作次数加1，直到有格子数值相同时结束游戏。

下图展示了一个最优的前两步操作示例。
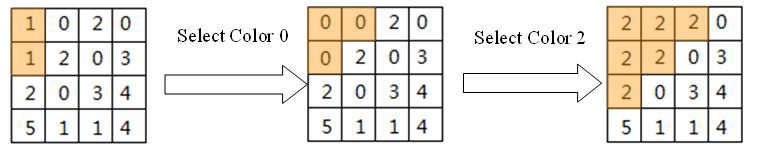  求最少的操作次数。

分析 ：和 UVa1499/LA5722 Gem And Prince 一个套路，上启发式搜索即可，本题是用 I D A ∗ IDA^* IDA∗ 算法。

预先处理初始网格的各个连通块并建立连通块之间的相邻关系。此后只需要在迭代加深搜索时处理当前左上角所在连通块向其相邻连通块的延伸即可。

启发函数：统计左上角所在连通块之外的其他连通块在 0 ∼ 5 0\sim 5 0∼5 的不同取值数 c，则至少还需要 c 步操作。

UVa11213 Flipull

题意 ：你是一滴橙色的液体，位于屏幕右方的梯子上。你可以向左方发射方块，消除同色方块，然后将碰到的第一个非同色方块变成发射的方块。你的目标是剩下不超过 b 个方块（如果最终有多于 b 个方块而无法继续操作时，你将输掉游戏）。

总共有 4 种方块，分别为蓝色的三角（T），粉红色的圆圈（O），绿色的方块（#）和十字叉（X）。发射之后，方块将持续往左飞行，直到遇到第一个不同的方块或者撞到墙壁（或者其他障碍物）。在第一种情况下，发射的方块将把原有的方块弹回你手里；在第二种情况下，发射的方块将改变方向，向下飞行，同样遇到第一个不同的方块时弹回你手里。如果向下飞行时落入底部，它将重返回你的手里。注意发射的方块必须至少消除一个同色方块。由于重力作用，当一个方块下方的方块消失时它会自然下落。除了上述 4 种方块之外，还有一种魔法方块（只可能在游戏开始时位于你的手中），发射后直接变成它所碰到的第一个方块，因此也称为万能方块，如下图（a）所示。

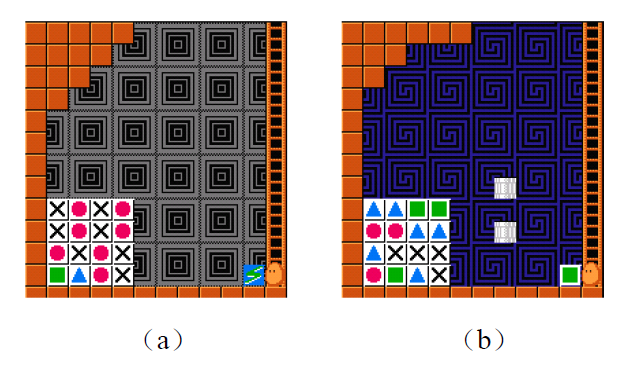
初始的游戏局面为 4×4、5×5 或者 6×6 大小，从底部到顶部行号依次编为 r 1 ∼ r 6 r1\sim r6 r1∼r6，从左到右列号依次被编为 c 1 ∼ c 6 c1\sim c6 c1∼c6。梯子上面总共有 12 格，从底部到顶部依次被编为 1 ∼ 12 1\sim12 1∼12。在图（a）中，由于墙壁能够反射方块，在 12 个位置发射方块实际是沿 r1，r2，r3，r4，c1，c1，c1，c1，c2，c3，c4，X 移动（X 代表在12 位置发射不会触碰到任何方块，因此是非法步骤）。图（b）有些许不同，管道也能反射方块，因此在 12 个位置发射事实上是沿 r1，r2，X，r4，X，c1，c1，c1，c1，c2，c3，X 移动。注意不可能沿着 r3 和 c4 移动。

下图所示是图（a）的求解过程（正好剩余 3 个方块），在 8，9，10，11 这 4个位置各发射一个方块，然后在 10 号位置发射，然后是 2 号位置，最后是 1 号位置。

你的任务是写一个程序，用最少的发射次数完成游戏。

分析 ：本题限时 30s，首先尝试 BFS 暴力求解，难点在于高效地对状态判重（直接用 set 超级慢），仔细分析本题特点，想到用字典树（Trie 树）对状态判重，单次代价仅 O ( n 2 ) O(n^2) O(n2)：由于 3<n<7，实际上很高效了。

可惜提交是 TLE 的，贴一个用于分析超时原因的好数据：

输入

xml 复制代码 
6 4 M
Game41
O#XTO#
XX#TTX
TO##XT
#OXTTT
OOTXO#
###TTO
r1 r2 r3 r4 r5 r6 c5 c3 c1 c4 c6 c3 
0

输出。

xml 复制代码 
Case 1: Game41
18
10 6 1 3 3 11 4 2 5 7 2 1 4 1 3 2 3 3

这条数据用 BFS 暴力求解运行时间 80 来秒，一下子就指明了 TLE 的原因，求解此条数据时状态数达到 7087199，说明 20 步以内有解时状态数可达 10 7 10^7 107 数量级。状态数太多，状态拓展和判重虽然高效但都是几十次的常数，不超时才怪。

还是得上启发式搜索，想办法对状态做剪枝，要分析一下怎么构造启发函数。沿着列向下发射时，最好的情况是整列都消除；沿着行向左发射时，最好的情况是整行都消除顺带将第一列的发射所在行以下的都消除。

那么可以在输入数据读入后用 dp 做一下预处理生成启发函数表：

考虑每列剩余的方块数 c i c_i ci，记 x = ∑ i = 0 n c i × 7 i \displaystyle x = \sum_{i=0}^{n} c_i\times7^i x=i=0∑nci×7i。当 ∑ i = 0 n c i ≤ b \displaystyle \sum_{i=0}^{n} c_i \le b i=0∑nci≤b 时不再需要发射， f ( x ) = 0 f(x) = 0 f(x)=0；否则然后枚举 12 个发射位置 j，按最好的情况消除计算得到每列剩余的方块数 c i ′ c^{'}i ci′，记 y j = ∑ i = 0 n c i ′ × 7 i \displaystyle y_j = \sum{i=0}^{n} c^{'}_i\times7^i yj=i=0∑nci′×7i，则 f ( x ) = 1 + m i n { f ( y j ) , 1 ≤ j ≤ 12 } f(x) = 1 + min\{f(y_j),1≤j≤12\} f(x)=1+min{f(yj),1≤j≤12}。

dp 预处理代价为 12 n ˉ × ( n + 1 ) 6 12\bar{n}\times(n+1)^6 12nˉ×(n+1)6，是 10 6 10^6 106 规模的常数，可以接受。

用 I D A ∗ IDA^* IDA∗ 算法，总步数为 maxd，当前已经操作了 s 步后状态编码为 x，则 s + f ( x ) > m a x d s + f(x) > maxd s+f(x)>maxd 时可以剪枝。

相关推荐
俩毛豆23 天前
基于HarmonyOS（NEXT）的超级App中的搜索架构实现（直播文字干货版）
成长·架构·app·harmonyos·搜索
課代表1 个月前
Windows 文本搜索命令 findstr
windows·正则表达式·命令行·文本·匹配·搜索·findstr
loong_XL1 个月前
腾讯元器自建联网搜索、百度官方搜索api
搜索
_OP_CHEN2 个月前
算法基础篇：（四）基础算法之前缀和
c++·算法·前缀和·蓝桥杯·acm·icpc·算法竞赛
_OP_CHEN2 个月前
算法基础篇：（五）基础算法之差分——以“空间”换“时间”
c++·算法·acm·icpc·算法竞赛·差分算法·差分与前缀和
惆怅客1232 个月前
UVa1497/LA5719 A Letter to Programmers
计算几何·icpc·uva·矩阵快速幂·三维变换矩阵
Juan_20122 个月前
P1041题解
c++·算法·题解·搜索
图灵信徒3 个月前
2024南京icpc区域赛详解与难点解释
c++·acm·icpc·算法竞赛
西望云天3 个月前
The 2024 ICPC Asia Nanjing Regional Contest（2024南京区域赛EJKBG）
数据结构·算法·icpc
热门推荐
01GitHub 镜像站点02手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04Linux下V2Ray安装配置指南05Labelme从安装到标注：零基础完整指南06jdk21下载、安装（Windows、Linux、macOS）07【踩坑笔记】50系显卡适配的 PyTorch 安装082025 最新教程：注册并切换到美区 Apple ID09UV安装并设置国内源10GitLab 零基础入门指南：从安装到项目管理全流程