泰勒定理与余项
定理 1 泰勒定理
对某个函数写出它的泰勒展开式,实际上没办法写出无穷多项出来,但常常只要写个前几项就已有不错的近似,写越多项就越逼近。如下图所示,sin(x)\sin(x)sin(x) 的麦克劳林展开,写得越多项,在 x=0x=0x=0 附近就与 sin(x)\sin(x)sin(x) 越像。
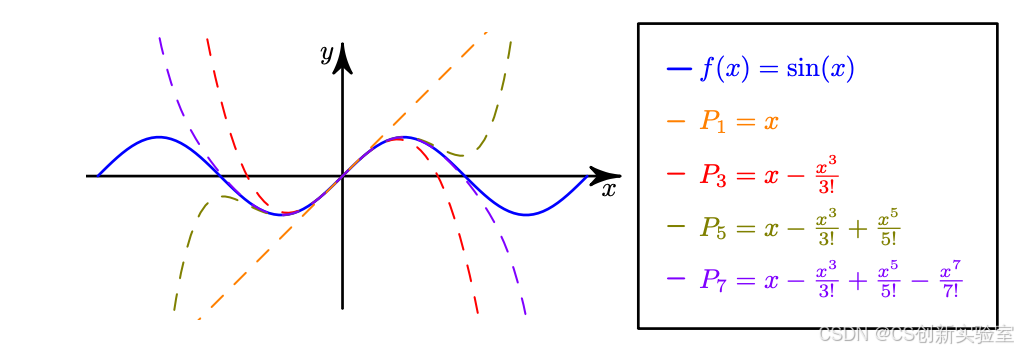
现在我们来讨论,如果预先想好要近似到某种准确度,譬如说想要准确到小数点后四位,能不能在展开前,预先估计一下大概要算几项呢?或者是,当写出 nnn 项出来,如何知道估计的近似值跟精确值的误差有多少呢?
定理 1 泰勒定理
若 f(x)f(x)f(x) 在某个包含 aaa 点的开区间 III 上 n+1n + 1n+1 阶可导,则对于任意的 x∈Ix \in Ix∈I , f(x)f(x)f(x) 都可以展开为:
f(x)=f(a)+f′(a)(x−a)+⋯+f(n)(a)n!(x−a)n+Rn(x) f(x) = f(a) + f'(a)(x - a) + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + R_n(x) f(x)=f(a)+f′(a)(x−a)+⋯+n!f(n)(a)(x−a)n+Rn(x)其中,Rn(x)=f(n+1)(c)(n+1)!(x−a)n+1(c 介于 x 和 a 之间)R_n(x) = \frac{f^{(n+1)}(c)}{(n+1)!}(x - a)^{n+1} \quad (c~介于~x~和~a~之间)Rn(x)=(n+1)!f(n+1)(c)(x−a)n+1(c 介于 x 和 a 之间)
这个定理告诉我们,如果一个函数在某个开区间上可以求导 17 次的话,那么我们就可以照着这个一般式来写出泰勒展开,写到第 16 阶。至于它与原来的函数的差,就用 R16(x)R_{16}(x)R16(x) 来代表这个差。也就是说:R16(x)=f(x)−p16(x)R_{16}(x) = f(x) - p_{16}(x)R16(x)=f(x)−p16(x) ,其中 p16(x)p_{16}(x)p16(x) 是展开到第 16 阶的泰勒多项式。
一般来说,展开出 nnn 阶的话,便有 Rn(x)R_n(x)Rn(x) 来代表差。也就是:
Rn(x)=f(x)−pn(x) R_n(x) = f(x) - p_n(x) Rn(x)=f(x)−pn(x)
其中 pn(x)p_n(x)pn(x) 是展开到第 nnn 阶的泰勒多项式。
这叫做余项 (remainder),也可称之为误差项 (error term)。在这定理中还告诉我们余项的形式,只要先照着泰勒多项式的一般项写法,写出下一项:
f(n+1)(c)(n+1)!(x−a)n+1 \frac{f^{(n+1)}(c)}{(n+1)!}(x - a)^{n+1} (n+1)!f(n+1)(c)(x−a)n+1
但注意 f(n+1)()f^{(n+1)}()f(n+1)() 里面,那里不是照着抄 aaa,而是改成某一个 ccc。这个 ccc 是介于 xxx 和 aaa 之间的某个数。这样写就刚好是原函数与 nnn 阶泰勒多项式之间的差。接着再把这个差,挂上绝对值,就是误差。也就是说:
误差=∣Rn(x)∣=∣f(x)−pn(x)∣=∣f(n+1)(c)(n+1)!(x−a)n+1∣ \text{误差} = \left| R_n(x) \right| = \left| f(x) - p_n(x) \right| = \left| \frac{f^{(n+1)}(c)}{(n+1)!}(x - a)^{n+1} \right| 误差=∣Rn(x)∣=∣f(x)−pn(x)∣= (n+1)!f(n+1)(c)(x−a)n+1
至于 ccc ,我们只知道是 xxx 和 aaa 间的某个数,并不知道到底是多少,这样有用吗?实际上我们可以用估计的方式,来说:无论 ccc 是何值,这个误差都小于等于某个值,如此一来虽无法确知误差是多少,但至少可确定误差不会超过那个值。
例 :用 5 阶泰勒多项式估计 sin(1)\sin(1)sin(1) 的近似值时,误差大约是多少?
解:
sin(x)\sin(x)sin(x) 的 5 阶麦克劳林展开式是:x−x33!+x55!x - \frac{x^3}{3!} + \frac{x^5}{5!}x−3!x3+5!x5
代入 x=1x = 1x=1 ,得到:
1−13!+15!=101120≈0.8416667 1 - \frac{1}{3!} + \frac{1}{5!} = \frac{101}{120} \approx 0.8416667 1−3!1+5!1=120101≈0.8416667
这就是对 sin(1)\sin(1)sin(1) 的估计值。
现在想知道,这个估计值与精确值的误差大概是多少。
余项为:R5(x)=f(6)(c)6!x6R_5(x) = \frac{f^{(6)}(c)}{6!}x^6R5(x)=6!f(6)(c)x6
由于是麦克劳林展开,所以 a=0a = 0a=0 ,接着代入 x=1x = 1x=1 ,且误差要取绝对值,因此应该写成:
∣R5(1)∣=∣f(6)(c)6!∣ \left| R_5(1) \right| = \left| \frac{f^{(6)}(c)}{6!} \right| ∣R5(1)∣= 6!f(6)(c)
而 sin(x)\sin(x)sin(x) 的 6 阶导函数是 −sin(x)-\sin(x)−sin(x) ,所以:
∣R5(1)∣=∣−sin(c)6!∣=∣sin(c)6!∣ \left| R_5(1) \right| = \left| \frac{-\sin(c)}{6!} \right| = \left| \frac{\sin(c)}{6!} \right| ∣R5(1)∣= 6!−sin(c) = 6!sin(c)
不知道 ccc 是多少没有关系,反正我们知道 ∣sin(x)∣≤1|\sin(x)| \leq 1∣sin(x)∣≤1 恒成立,所以可以说:
∣R5(1)∣=∣sin(c)6!∣≤16!=1720≈0.0013889 \left| R_5(1) \right| = \left| \frac{\sin(c)}{6!} \right| \leq \frac{1}{6!} = \frac{1}{720} \approx 0.0013889 ∣R5(1)∣= 6!sin(c) ≤6!1=7201≈0.0013889
这样写的意思是,我们不知道误差的具体大小,但至少可以确定它不会超过 0.00138890.00138890.0013889 。或许实际上 ccc 离 0 很近,使得 sin(c)\sin(c)sin(c) 很小,也就是说误差值实际上远小于 0.00138890.00138890.0013889 。但不管怎样,至少能确定它一定不会超过 0.00138890.00138890.0013889 。
实际用数学软件计算 ∣sin(1)−101120∣\left| \sin(1) - \frac{101}{120} \right| sin(1)−120101 ,得到大约是 0.0001956820.0001956820.000195682 ,确实比 0.00138890.00138890.0013889 小很多,还不到它的六分之一。
现在已经对余项的内容有所了解,接下来分析收敛区间。首先必须郑重强调的是,同样是 "收敛区间",泰勒展开的收敛区间与幂级数的收敛区间,意义并不相同。
幂级数的收敛区间是指,只要 xxx 在这个区间内,代入幂级数后所形成的无穷级数会收敛。而泰勒展开的收敛区间是指,只要 xxx 在这个区间内,代入泰勒级数后所形成的无穷级数不但会收敛,还等于直接将 xxx 代入原函数所得的结果。
举个例子,理解上述区别:
f(x)={e−1x2,x≠00,x=0 f(x)= \begin{cases} e^{-\frac{1}{x^2}} ,&x \neq 0 \\ 0 ,&x=0 \end{cases} f(x)={e−x21,0,x=0x=0
它在 x=0x = 0x=0 处的各阶导数都是 0,即:f(0)=f′(0)=f′′(0)=⋯=0f(0) = f'(0) = f''(0) = \cdots = 0f(0)=f′(0)=f′′(0)=⋯=0
于是它的麦克劳林展开式为:
0+0+0+⋯(3.1) 0 + 0 + 0 + \cdots \tag{3.1} 0+0+0+⋯(3.1)
这个形式特殊的 "幂级数",无论代入什么 xxx 值,每一项都是 0,所以幂级数的收敛区间是 (−∞,+∞)(-\infty, +\infty)(−∞,+∞)。但函数 f(x)f(x)f(x) 只有在 x=0x = 0x=0 时函数值为 0,在其他点的函数值都不为 0,因此泰勒展开的收敛区间只有 x=0x = 0x=0 这一点。
定理 2 皮亚诺型余项的泰勒定理
以下再从拉格朗日均值定理的角度理解泰勒展开的余项。首先了解拉格朗日均值定理:
对于一个在给定区间上满足特定条件的函数,在该区间内至少存在一点,使得该点的切线斜率等于区间两端点连线的斜率。
设函数 f(x) 满足以下条件:
- 在闭区间 [a, b] 上连续。
- 在开区间 (a, b) 内可导。
那么,在开区间 (a, b) 内至少存在一点 c (a < c < b),使得以下等式成立:
f′(c)=[f(b)−f(a)]/(b−a) f'(c) = [f(b) - f(a)] / (b - a) f′(c)=[f(b)−f(a)]/(b−a)
拉格朗日均值定理指出,对于一条光滑连续的曲线,在任意两点之间,总能找到至少一个点,使得曲线在该点的切线平行于连接这两点的弦。它揭示了函数在区间上的平均变化率必然等于其内部某一点的瞬时变化率。
仔细一看,它其实就是零阶泰勒展开 f(x)=f(a)+R0(x)f(x) = f(a) + R_0(x)f(x)=f(a)+R0(x) 然后再代入x=bx = bx=b 而已!所以带有拉格朗日型余项的泰勒定理,其实就是更高阶的均值定理。
余项的另一种写法,叫做皮亚诺型余项(Peano form of the remainder)。
定理 2 皮亚诺型余项的泰勒定理
若 f(x)f(x)f(x) 在某个包含 aaa 点的开区间 III 上 n+1n + 1n+1 阶可导,则对于任意的 x∈Ix \in Ix∈I,f(x)f(x)f(x) 都可以展开为:
f(x)=f(a)+f′(a)(x−a)+⋯+f(n)(a)n!(x−a)n+Rn(x) f(x) = f(a) + f'(a)(x - a) + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + R_n(x) f(x)=f(a)+f′(a)(x−a)+⋯+n!f(n)(a)(x−a)n+Rn(x)其中,Rn(x)=o((x−a)n)R_n(x) = o\left((x - a)^n\right)Rn(x)=o((x−a)n)
这种写法涉及了 Landau 小 ooo 记号,这是德国数学家 Edmund Landau 用来描述函数的渐近行为的符号。如果 limx→0f(x)x3=0\lim\limits_{x \to 0} \frac{f(x)}{x^3} = 0x→0limx3f(x)=0,记为 f(x)=o(x3)f(x) = o(x^3)f(x)=o(x3),意思是说 f(x)f(x)f(x) 是比 x3x^3x3 更高阶的无穷小。换句话说,f(x)f(x)f(x) 趋向于 0 的速度比 x3x^3x3 趋向于 0 的速度还要快!
皮亚诺型余项的写法是通过简单标注高阶无穷小来体现的。例如,指数函数 exe^xex 的泰勒展开式原本写为:
ex=1+x+x22!+x33!+x44!+⋯ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots ex=1+x+2!x2+3!x3+4!x4+⋯
而带有皮亚诺型余项的写法则是:
ex=1+x+x22!+x33!+x44!+o(x4) e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + o(x^4) ex=1+x+2!x2+3!x3+4!x4+o(x4)
口语上来说,就是 x44!\frac{x^4}{4!}4!x4 这一项之后没有写出的部分,都是比 x4x^4x4 更高阶的无穷小。
例如利用泰勒展开求极限,如:
limx→0tan(x)−sin(x)x3=limx→0(x+x33+⋯ )−(x−x33!+⋯ )x3=limx→0x32+⋯x3=12 \lim_{x \to 0} \frac{\tan(x) - \sin(x)}{x^3} = \lim_{x \to 0} \frac{\left( x + \frac{x^3}{3} + \cdots \right) - \left( x - \frac{x^3}{3!} + \cdots \right)}{x^3} = \lim_{x \to 0} \frac{\frac{x^3}{2} + \cdots}{x^3} = \frac{1}{2} x→0limx3tan(x)−sin(x)=x→0limx3(x+3x3+⋯)−(x−3!x3+⋯)=x→0limx32x3+⋯=21
现在用带有皮亚诺型余项的写法可以表示为:
limx→0tan(x)−sin(x)x3=limx→0(x+x33+o(x3))−(x−x33!+o(x3))x3 \lim_{x \to 0} \frac{\tan(x) - \sin(x)}{x^3} = \lim_{x \to 0} \frac{\left( x + \frac{x^3}{3} + o(x^3) \right) - \left( x - \frac{x^3}{3!} + o(x^3) \right)}{x^3} x→0limx3tan(x)−sin(x)=x→0limx3(x+3x3+o(x3))−(x−3!x3+o(x3))
进一步化简:
=limx→0x32+o(x3)x3=12 = \lim_{x \to 0} \frac{\frac{x^3}{2} + o(x^3)}{x^3} = \frac{1}{2} =x→0limx32x3+o(x3)=21
比起原本用省略号的写法,带有皮亚诺型余项的写法明确指出了哪些是更高阶的无穷小,因此在计算极限时,这些高阶无穷小项是可以略去不考虑的。
定理 3 积分型余项的泰勒定理
定理 3 积分型余项的泰勒定理
若函数 f(x)f(x)f(x) 在某个包含点 aaa 的开区间 III 上存在 n+1n+1n+1 阶导数,且 f(n+1)(x)f^{(n+1)}(x)f(n+1)(x) 在该区间上连续,则对于任意 x∈Ix \in Ix∈I , f(x)f(x)f(x) 可以展开为:
f(x)=f(a)+f′(a)(x−a)+⋯+f(n)(a)n!(x−a)n+Rn(x) f(x) = f(a) + f'(a)(x-a) + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x) f(x)=f(a)+f′(a)(x−a)+⋯+n!f(n)(a)(x−a)n+Rn(x)其中,积分型余项 Rn(x)R_n(x)Rn(x) 为:
Rn(x)=∫axf(n+1)(t)n!(x−t)n dt R_n(x) = \int_a^x \frac{f^{(n+1)}(t)}{n!} (x-t)^n \, dt Rn(x)=∫axn!f(n+1)(t)(x−t)ndt
由微积分基本定理:
f(x)=f(a)+∫axf′(t) dt f(x) = f(a) + \int_a^x f'(t) \, dt f(x)=f(a)+∫axf′(t)dt
对上述积分进行分部积分,过程如下:
f(x)=f(a)+[(t−x)f′(t)]ax−∫ax(t−x)f′′(t) dt=f(a)+(x−a)f′(a)−∫ax(t−x)f′′(t) dt \begin{align*} f(x) &= f(a) + \left[ (t-x)f'(t) \right]_a^x - \int_a^x (t-x)f''(t) \, dt \\ &= f(a) + (x-a)f'(a) - \int_a^x (t-x)f''(t) \, dt \end{align*} f(x)=f(a)+[(t−x)f′(t)]ax−∫ax(t−x)f′′(t)dt=f(a)+(x−a)f′(a)−∫ax(t−x)f′′(t)dt
继续对剩余积分做分部积分:
f(x)=f(a)+(x−a)f′(a)−[(t−x)22f′′(t)]ax+∫ax(t−x)22f′′′(t) dt=f(a)+(x−a)f′(a)+(x−a)22f′′(a)+∫ax(t−x)22f′′′(t) dt \begin{align*} f(x) &= f(a) + (x-a)f'(a) - \left[ \frac{(t-x)^2}{2} f''(t) \right]_a^x + \int_a^x \frac{(t-x)^2}{2} f'''(t) \, dt \\ &= f(a) + (x-a)f'(a) + \frac{(x-a)^2}{2} f''(a) + \int_a^x \frac{(t-x)^2}{2} f'''(t) \, dt \end{align*} f(x)=f(a)+(x−a)f′(a)−[2(t−x)2f′′(t)]ax+∫ax2(t−x)2f′′′(t)dt=f(a)+(x−a)f′(a)+2(x−a)2f′′(a)+∫ax2(t−x)2f′′′(t)dt
如此反复进行分部积分,最终可得:
f(x)=f(a)+(x−a)f′(a)+(x−a)22!f′′(a)+⋯+(x−a)nn!f(n)(a)+Rn(x) f(x) = f(a) + (x-a)f'(a) + \frac{(x-a)^2}{2!} f''(a) + \cdots + \frac{(x-a)^n}{n!} f^{(n)}(a) + R_n(x) f(x)=f(a)+(x−a)f′(a)+2!(x−a)2f′′(a)+⋯+n!(x−a)nf(n)(a)+Rn(x)
其中,余项可整理为:
Rn(x)=(−1)n∫ax(t−x)nn!f(n+1)(t) dt=∫ax(x−t)nn!f(n+1)(t) dt R_n(x) = (-1)^n \int_a^x \frac{(t-x)^n}{n!} f^{(n+1)}(t) \, dt = \int_a^x \frac{(x-t)^n}{n!} f^{(n+1)}(t) \, dt Rn(x)=(−1)n∫axn!(t−x)nf(n+1)(t)dt=∫axn!(x−t)nf(n+1)(t)dt
从微积分基本定理出发,通过反复分部积分可推导出带有积分型余项的泰勒定理。因此,泰勒定理也可看作是微积分基本定理的推广。
泰勒理论是微分学的巅峰。它是高阶逼近,相比切线的一阶逼近,精度更高;它是微积分基本定理的推广,也是高阶的拉格朗日中值定理。在应用上,它可轻松求解极限、估计函数值与积分,还能证明极值理论。学习泰勒理论时,常会有 "会当凌绝顶,一览众山小" 之感!