问题是一步一步解决的,将简单的工具组合起来就可以解决似乎没有头绪的问题。
先让n=2n,表示序列的总长度。
先考虑k=1的情况,对于这种"括号序列"问题,如果遇到A让y加1,遇到C让y减1,可以在坐标轴上画出图像,对某个x,y>=0,代表长度为x的前缀满足A的数量>=C的数量,y<0则不满足,所以,进行变换之后的图像,要满足所有点(对所有x)y都大于等于0。
这个图像一定是从y=0开始,到y=0结束,因为一开始没有A和C,A和C数量相等,整个序列中A和C数量相同,所以最后x=n时,y=0。
以ACCCAACAAAACCC为例,图像如下:
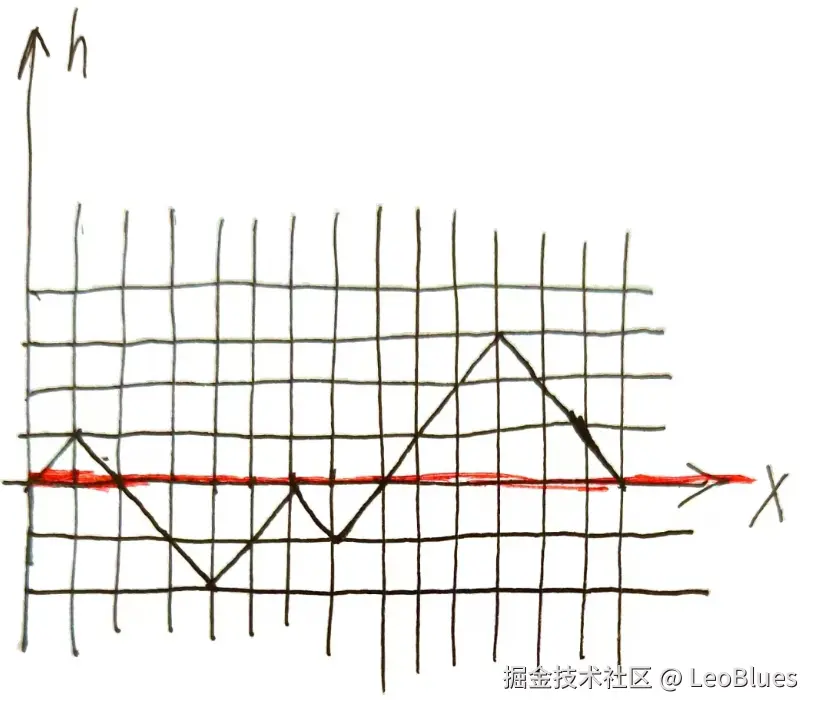
接着如果没有第一步的反转操作,只有交换相邻两个字母,将所有的h(也就是之前说的y)变为>=0,需要多少次呢?
我们分类讨论看看: 交换AA或者CC是没有意义的。 将AC变成CA,第一个位置的值减少2,其他位置的值都没有变。要通过交换增加某个x对应的h,这种操作反而减少了h,是不应该采取的。 将CA变成AC,第一个位置的值增加2,其他位置的值不变,因此,一次CA的交换可以让C这个位置的值增加2。 按照以下方法可以保证每次总能找到CA对交换:找到最靠左的负位置,这个位置的高度一定是-1,因此这个位置上的字母一定是C,这个位置右边一定有A,因为最后到第n个位置高度是0,后面必须有A来让高度增加。将在这个位置 右边离其最近的A交换到当前位置,要么是C A,要么是C....CA,这个过程中每次CA交换都能起到效果让负高度增加2的效果。因此,每次都能找到CA对,且每次交换能起到高度+2的效果,
如果每个高度是负数的位置:p1,p2...pm。
那么最少的交换次数是:ceil(-h_p1/2)+ceil(-h_p2/2)+...+ceil(-h_pm/2)。
接下来看看反转操作对x-h图像有什么作用:
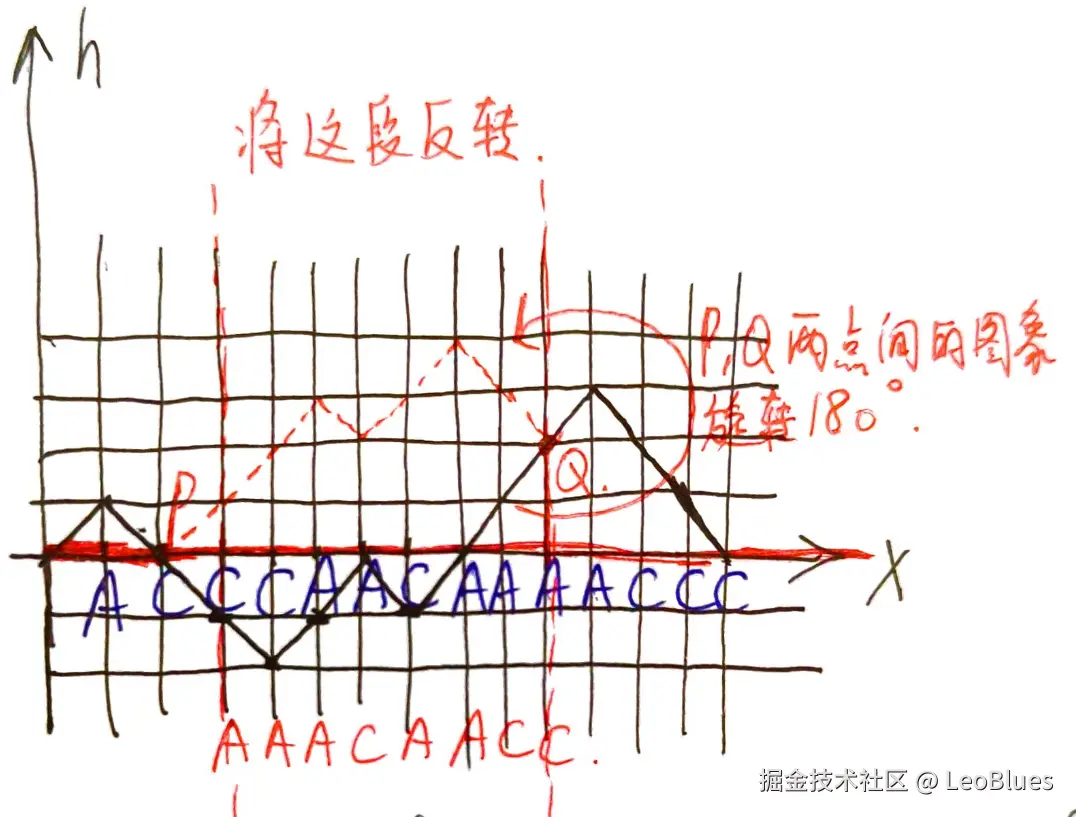
可见,反转的效果是选定一组(l,r) (l<r且l,r间的距离大于1,实际上,即使等于1也不影响),将[l,r]间的图像旋转180度。
反转之后,位置i的新高度是h_p-(h_i-h_q),因为旋转前,从q开始从右向左看高度相对于q是正数的点,从p开始从左向右看,相对于p的高度是同等大小的负数。
h_i_new=h_p+h_q-h_i,因此原高度如果大于(h_p+h_q),则旋转后高度为负数。得知旋转后的新高度,可以用之前计算最少交换次数的方法,计算[l,r]间的,再计算[l,r]外左右两边的,来获得最少交换次数。
如果l和r从1到n遍历,复杂度是n^2,l和r的选取有哪些特征吗:
将图像分为正的"块"和负的"块",如图,用红色描出的为正,蓝色为负:
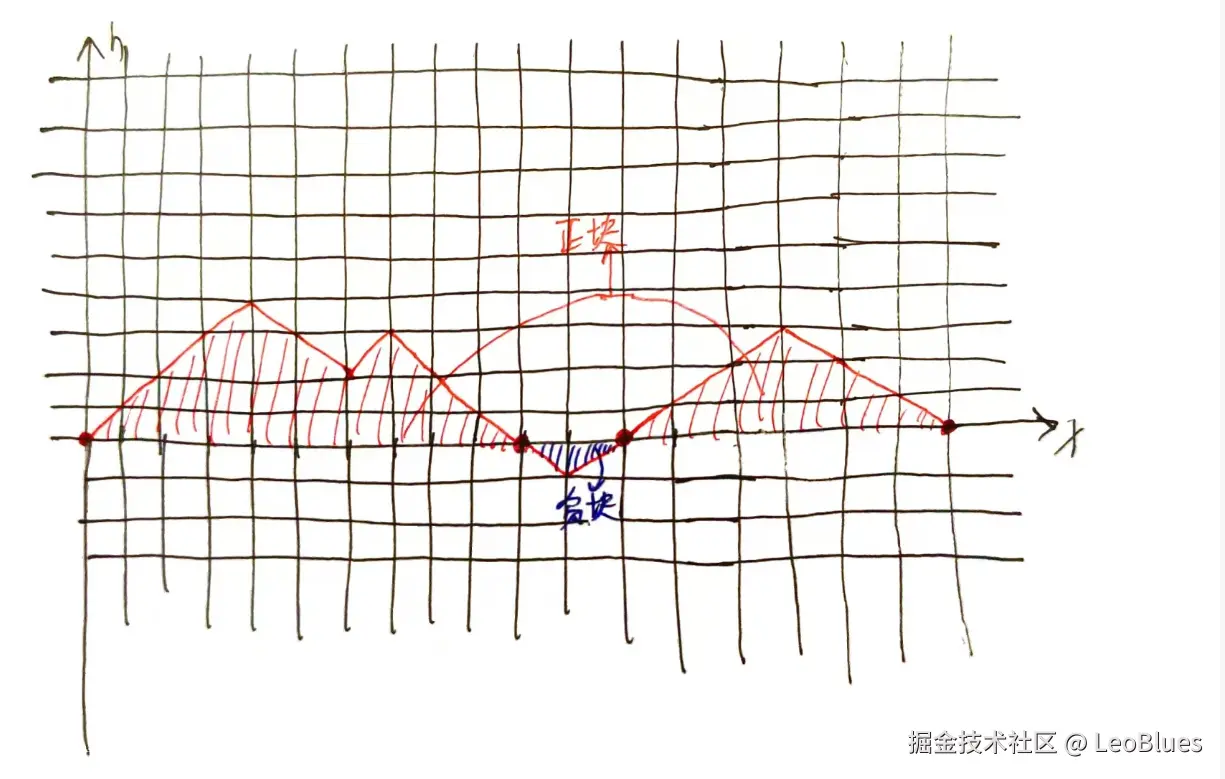
1.如果l选到了高度小于0的位置,将l向左移动到第一个高度为0的位置,则[l,r]间的负部分减少了,[l,r]外的负部分也减少,所以l应该选择高度>=0的位置,同样,r也是。
2.因此,l和r应该在"正"块中选点,且在一个正块中,l应该选这个块中高度最大的点,这是因为,[l,r]外的负点不会变多,h_l增大,[l,r]间高度大于h_l+h_r的点会减少,结果不会更劣。同样,r应该选一个正块中高度最大的点。
3.已知1,2,我们知道l选择的是每个正块中高度最高的点,让这些点是p1,p2,p3....。
我们只挑选最大高度被更新的点,理由:如果一个p_i的高度相较之前的最大高度p_j小或相等,将l从p_i改成p_j,[l,r]间的负部分不会增加,[l,r]外的负部分只有可能减少,结果不会更劣。下图中的l候选对象是p1,p2,p5。
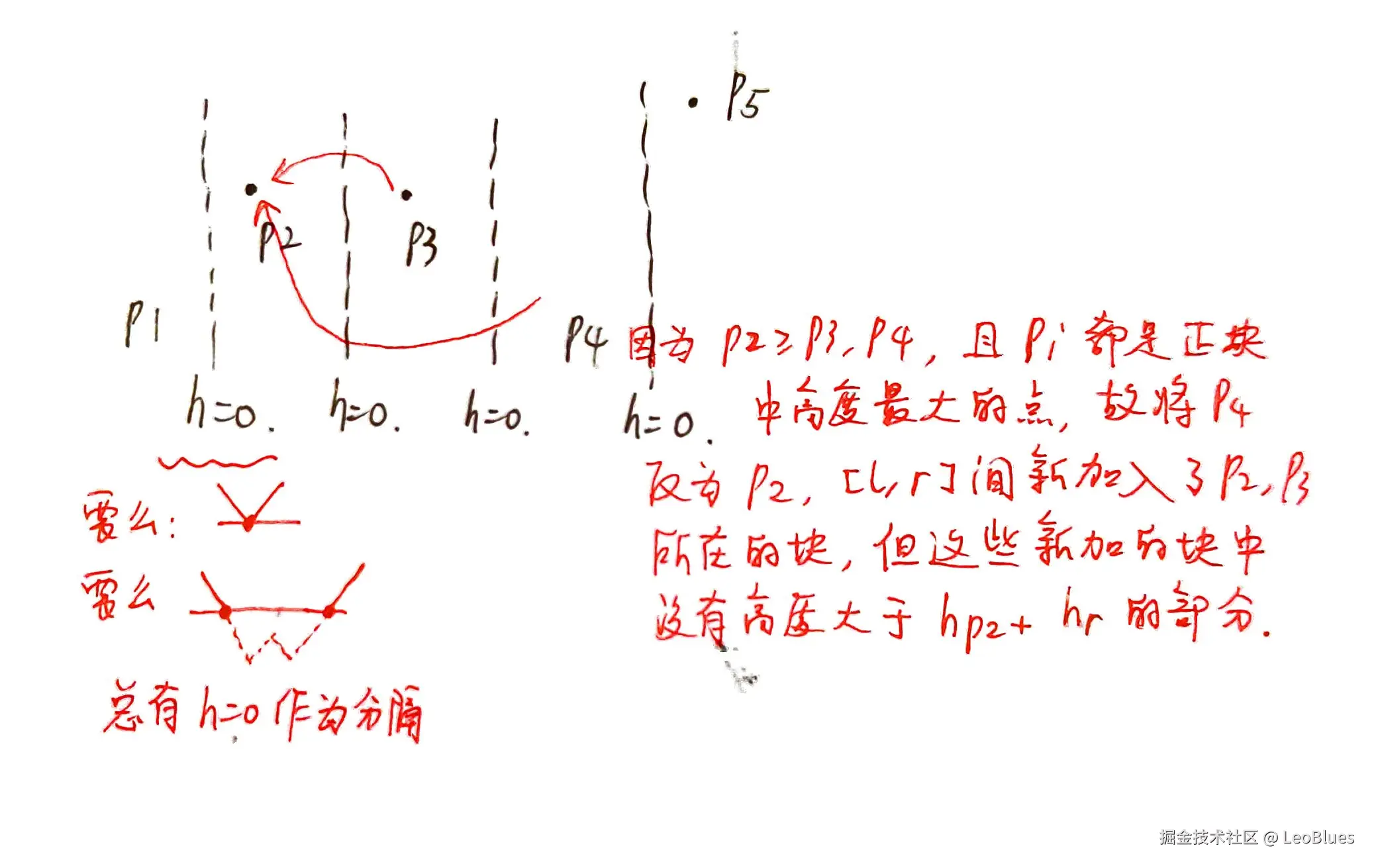
同理,r是从右向左最大高度被更新的点。
有了以上的特殊性质,(l,r)对还有多少个?让l和r的候选对象尽量多的图像如下:
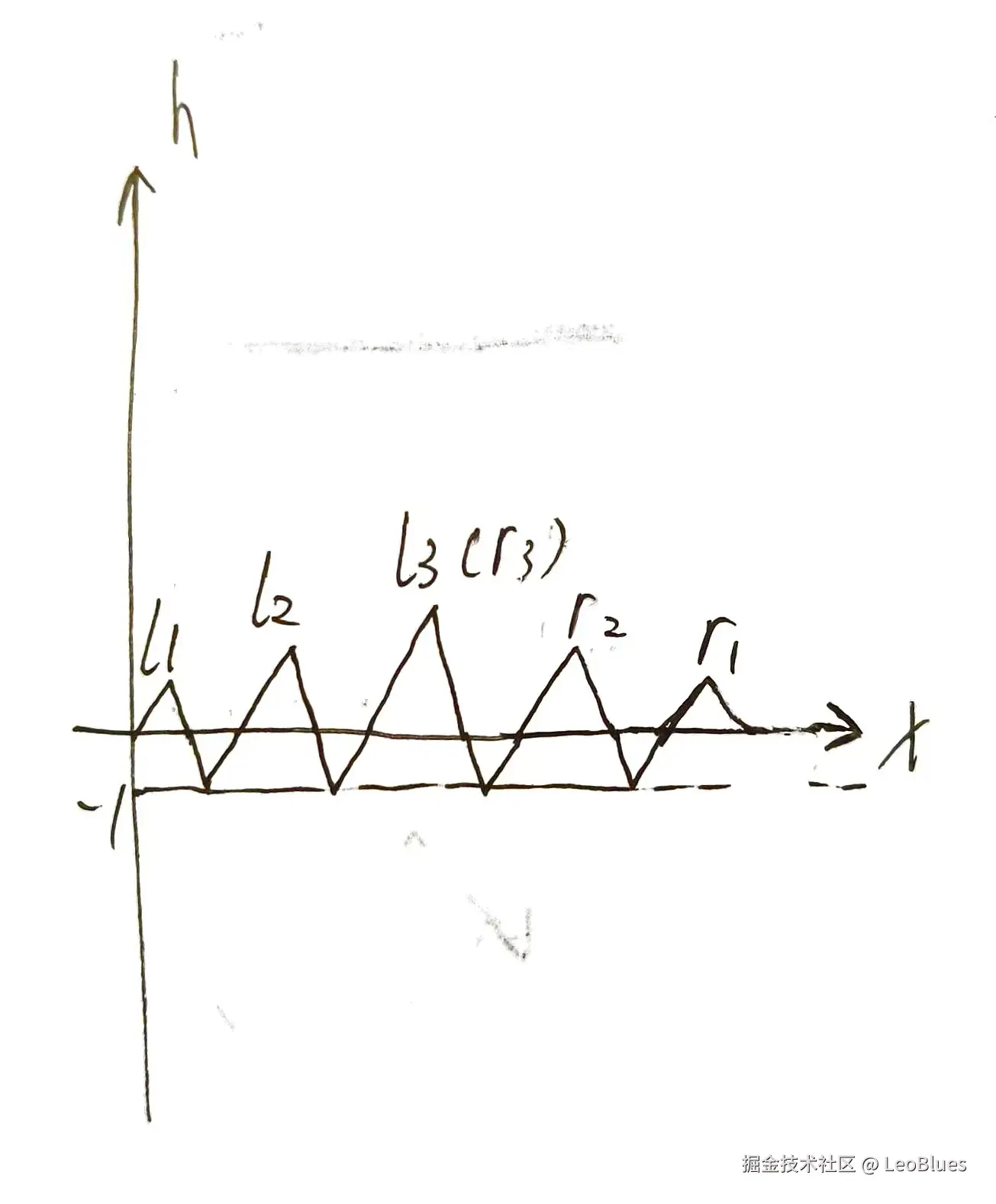
如果l和r都有x个候选对象,那么 [2x(这是每个候选对象带的-1)+2(1+2+...+x)]*2=n,计算得到x在根号n级别。这样 (l,r)对有n个,复杂度ok。
获得(l,r)对以后,需要以O(1)时间计算出第二步的交换需要多少次,用c_l表示l左边ceil(负高度/2)的和,c_r表示r右边ceil(负高度/2)的和,但[l,r]间的部分怎么处理呢?这部分需要的交换次数是:若h=h_l+h_r,令c_h表示整个序列ceil((大于等于h的高度-h)/2)的和,则需要的c_h是需要的次数。为什么是整个序列?因为l左边和r右边其实没有高度大于等于h的点。我们预处理出c_l,c_r,c_h就可以了。
在实现过程中,可以这样计算c_h:
用奇偶分类的方式:c_h_even是h,h+2,h+4,h+6...这些高度需要的交换次数,c_h_odd是h+1,h+3...这些高度需要的交换次数。
让cnt[i]代表高度为i的点的数量,pref[i]是cnt[i]+cnt[i+2]+cnt[i+4]+...,则c_h_even[i]=c_h_even[i+2]+pref[i+2],下图中ch代表c_h_even,计算原理如下图:
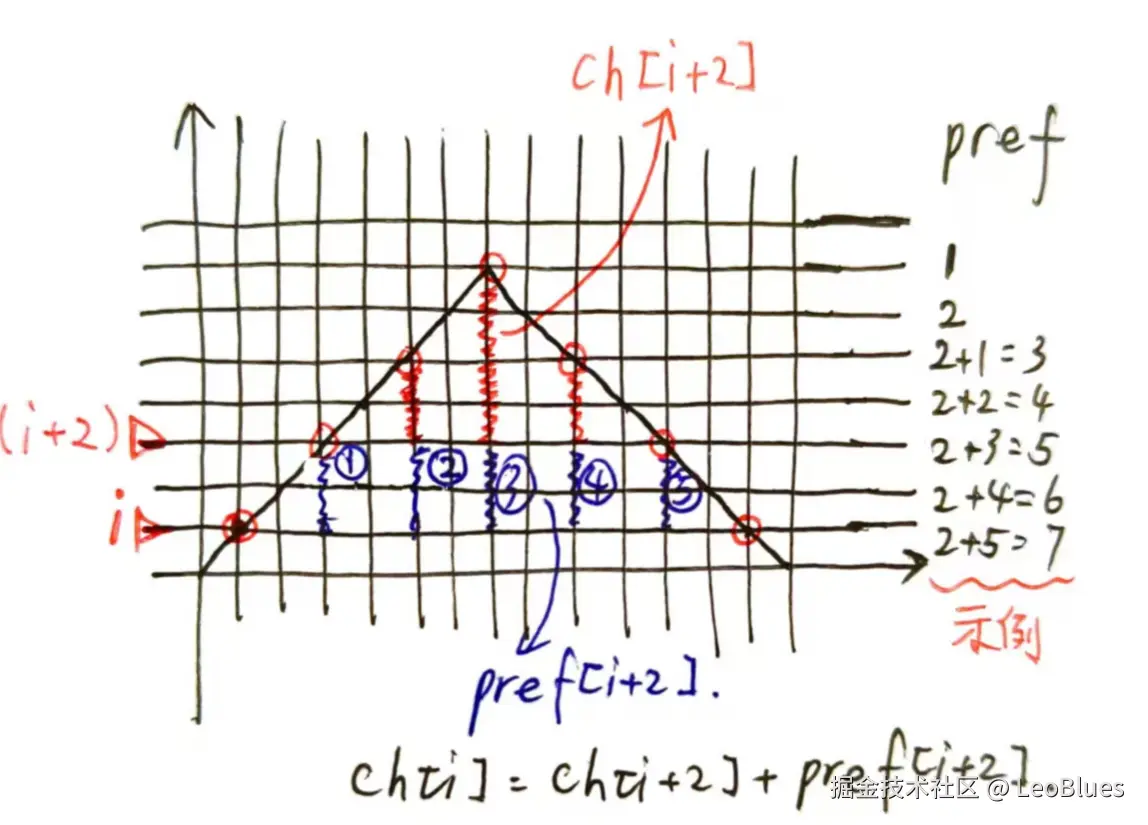
得到c_h_even后,c_h_odd[i]=c_h_even[i+1]+pref[i+1],原理如下:
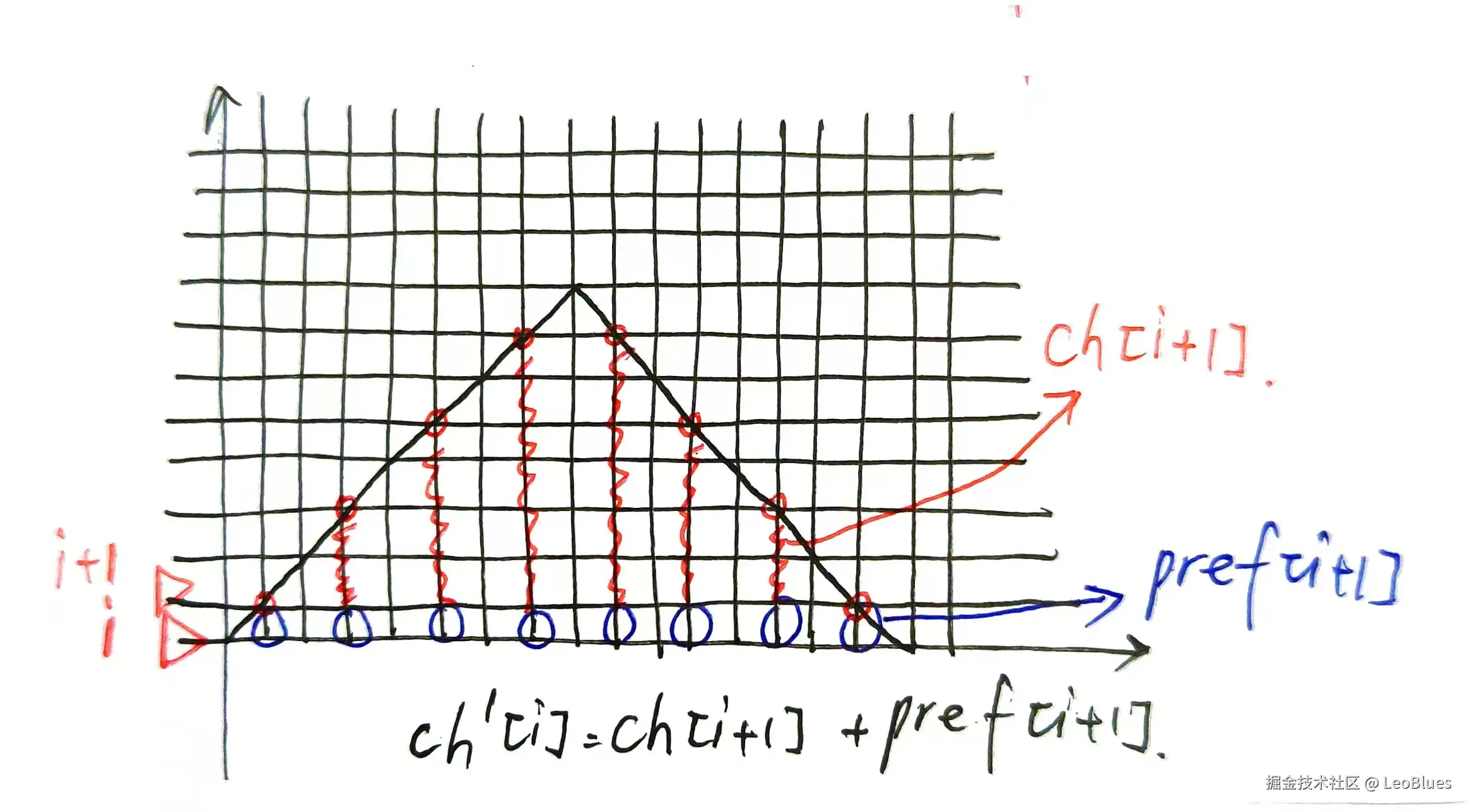
将k拓展到>1:因为l,r的选取特点,l'选的是第一个序列的l,r'选的是最后一个(也就是第k个)序列的r,那么l和r中间需要的交换次数是k*c_h,左右两边需要的还是c_l和c_r。
之后对每个(l,r)对,h=h_l+h_r,则所需交换次数是:c_l+c_r+k* c_h,如果只有一个k,遍历所有(l,r)取最大即可,但现在有多个k,则问题变为y=k* x+b,有n组(x,b)和K组k,可以使用带斜率优化的动态规划来找到y的最小值。
cpp
/*
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fio ios::sync_with_stdio(0);cin.tie(0);
#define fin freopen("D:/in.txt","r",stdin);
#define fout freopen("D:/out.txt","w",stdout);
const ll maxn=1e6*2+5;
ll n,k,lcnt,rcnt,pcnt;
string s;
ll h[maxn],l[maxn],r[maxn],ch[maxn],cl[maxn],cr[maxn],ch_even[maxn],ch_odd[maxn],pref[maxn],cnt[maxn],ans[maxn],q[maxn];
struct Point{
ll x,y;
bool operator < (const Point &rhs) const {
if(x==rhs.x) return y<rhs.y;
return x<rhs.x;
}
bool operator == (const Point &rhs) const {
return (x==rhs.x && y==rhs.y);
}
}point[maxn];
double slope(ll i,ll j) {
ll x_1=point[i].x,y_1=point[i].y;
ll x_2=point[j].x,y_2=point[j].y;
if(x_1==x_2) return 1e12;
else return (double)(y_2-y_1)/(double)(x_2-x_1);
}
ll comp_slope(ll i1,ll j1,ll i2,ll j2) {
__int128 dx1=point[j1].x-point[i1].x,dy1=point[j1].y-point[i1].y;
__int128 dx2=point[j2].x-point[i2].x,dy2=point[j2].y-point[i2].y;
if(dx1==0 && dx2==0) return 1;
if(dx1==0) return 2;
if(dx2==0) return 0;
if(dy1*dx2==dy2*dx1) return 1;
if(dy1*dx2<dy2*dx1) return 0;
if(dy1*dx2>dy2*dx1) return 2;
return 0;
}
ll comp_slope2(ll i,ll j,ll tocomp) {
__int128 dx=point[j].x-point[i].x,dy=point[j].y-point[i].y;
if(dx==0) return 2;
if(dy==(__int128)tocomp*dx) return 1;
if(dy<(__int128)tocomp*dx) return 0;
if(dy>(__int128)tocomp*dx) return 2;
return 0;
}
int main()
{
fio;
cin>>n>>k>>s;
n=n*2;
for(ll i=0;i<s.size();i++) {
if(s[i]=='A') h[i+1]=h[i]+1;
else h[i+1]=h[i]-1;
if(h[i+1]>=0) cnt[h[i+1]]++;
}
//获得l[]和r[]
//l[i]:第i个l点的横坐标(1-indexed)
ll lst=-1;
ll curmax=-1,candi=-1;
for(ll i=0;i<=n;i++) {
if(h[i]>curmax) {
curmax=h[i];
candi=i;
}
if(h[i]==0 && i!=0) { //连通块结束
if(curmax>=0 && curmax>lst) {
l[++lcnt]=candi;
lst=curmax;
}
}
}
lst=-1;
curmax=-1,candi=-1;
for(ll i=n;i>=0;i--) {
if(h[i]>curmax) {
curmax=h[i];
candi=i;
}
if(h[i]==0 && i!=n) { //连通块结束
if(curmax>=0 && curmax>lst) {
r[++rcnt]=candi;
lst=curmax;
}
}
}
/*//debug:查看选出的l,r
printf("l:\n");
for(ll i=1;i<=lcnt;i++) cout<<l[i]<<" ";
puts("");
printf("r:\n");
for(ll i=1;i<=rcnt;i++) cout<<r[i]<<" ";
puts("");
*/
//计算cl,cr
ll dep=0,nxtid=1;
for(ll i=0;i<=n;i++) {
if(h[i]<0) dep+=(-h[i]+1)/2;
if(i==l[nxtid]) {
cl[nxtid]=dep;
nxtid++;
}
if(nxtid>lcnt) break;
}
dep=0,nxtid=1;
for(ll i=n;i>=0;i--) {
if(h[i]<0) dep+=(-h[i]+1)/2;
if(i==r[nxtid]) {
cr[nxtid]=dep;
nxtid++;
}
if(nxtid>rcnt) break;
}
//计算ch
ll maxh=*max_element(h,h+1+n);
for(ll i=maxh;i>=0;i--) {
pref[i]=cnt[i]+pref[i+2];
ch_even[i]=ch_even[i+2]+pref[i+2];
}
for(ll i=maxh;i>=0;i--) {
ch_odd[i]=pref[i+1]+ch_even[i+1];
ch[i]=ch_even[i]+ch_odd[i];
}
pcnt=0;
for(ll i=1;i<=lcnt;i++) {
for(ll j=1;j<=rcnt;j++) {
Point tmp;
tmp.x=-ch[ h[l[i]]+h[r[j]] ];
tmp.y=cl[i]+cr[j];
point[++pcnt]=tmp;
}
}
stable_sort(point+1,point+1+pcnt);
pcnt=unique(point+1,point+1+pcnt)-(point+1);
ll head=1,tail=0;
for(ll i=1;i<=pcnt;i++) {
//while(tail>head && slope(q[tail],i)<=slope(q[tail-1],q[tail])) tail--;
while(tail>head && comp_slope(q[tail],i,q[tail-1],q[tail])<2) tail--;
q[++tail]=i;
}
/*
//debug
puts("开始输出点");
for(ll i=1;i<=tail;i++) {
ll j=q[i];
cout<<point[j].x<<" "<<point[j].y<<"\n";
}
puts("输出点结束");
puts("开始输出每段斜率");
for(ll i=2;i<=tail;i++) {
cout<<slope(q[i],q[i-1])<<"\n";
}
puts("输出斜率结束");
*/
for(ll i=1;i<=k;i++) {
ll curk=i;
while(head<tail && comp_slope2(q[head],q[head+1],curk)<=1) head++;
//while(head<tail && slope(q[head],q[head+1])<curk) head++;
//debug
//printf("k=%lld选点%lld\n",curk,head);
ans[i]=point[q[head]].y-point[q[head]].x*curk;
}
for(ll i=1;i<=k;i++) {
cout<<ans[i]<<"\n";
}
return 0;
}