引言:当"先有鸡还是先有蛋"遇到机器学习
假设你有两枚外观相同的硬币,它们被设计成抛出正面的概率不同,但你既不知道每次用的是哪枚,也不知道它们各自的真实概率。可能是硬币A是70%,硬币B是30%;也可能是硬币A是80%,硬币B是20%------你对此完全一无所知。
现在,你进行了100次实验:
- 每次实验,你随机拿起一枚硬币(但你不知道拿的是哪一枚)
- 将这枚硬币抛掷10次,记录正反面结果
- 重复这个过程
现在你只有100组抛掷结果。挑战来了:如何从这些数据中,**同时推断出两枚硬币各自的正面概率?**仔细分析这个问题,你会发现你同时面临两个"不知道":
- 不知道隐变量:对于每一次实验,你都不知道自己用的是硬币A还是硬币B
- 不知道参数:你也不知道两枚硬币各自的正面概率是多少
这形成了经典的"鸡生蛋"困局:
- 要知道每次用的硬币,需要知道硬币的概率
- 要知道硬币的概率,又需要知道每次用的硬币
- 简单平均所有数据只会得到一个混合概率,无法揭示两枚硬币的真实情况。
EM算法通过"先猜后证"的迭代方式破解这个困局:
- 先猜:随机假设两枚硬币的概率,如硬币A=0.6,硬币B=0.5
- 分配:基于假设,评估每组数据来自各硬币的可能性
- 修正:根据可能性重新计算概率
- 重复:用新概率重新分配,再修正,直到结果稳定
这个看似循环的方法,实际上包含强大的自我修正能力。如果硬币A的真实概率更高,那么抛出较多正面的结果自然会更多被分配给它,从而在修正时提高它的概率估计。反之,硬币B则会得到更多反面数据,降低其概率估计。这形成了"分配强化估计,估计改进分配"的正向循环。即使从错误的初始猜测开始,经过多次迭代,两枚硬币的概率也会逐渐分开,最终逼近真实值。
EM算法揭示了一个深刻道理:面对双重未知,我们可以从任意起点开始,让数据引导我们逐步逼近真相。这不仅是机器学习的核心思想,也反映了人类认知世界的基本方式------通过不断的假设、验证和修正,在不确定性中寻找确定性。
一、EM算法手动推导:抛硬币例子详解
1.1 符号定义
- 两枚硬币:硬币A和硬币B
- 硬币A的正面概率:θA\theta_AθA(待估计)
- 硬币B的正面概率:θB\theta_BθB(待估计)
- 实验轮数:n=5n=5n=5轮
- 每轮抛掷次数:m=10m=10m=10次
- 第iii轮观测数据:xix_ixi 是10次抛掷的具体正反面序列
- 我们记 hih_ihi 为第iii轮观测中正面出现的次数,ti=10−hit_i = 10 - h_iti=10−hi 为反面次数
- 隐变量:zi∈{A,B}z_i \in \{A, B\}zi∈{A,B},表示第iii轮选择的硬币
重要说明 :由于每次抛掷是独立的,任何具有相同正面次数hhh的序列都具有相同的概率。具体来说,如果硬币正面概率为θ\thetaθ,那么产生一个具体序列(包含hhh次正面和ttt次反面)的概率为 θh(1−θ)t\theta^h (1-\theta)^tθh(1−θ)t。在比较不同硬币产生该序列的概率时,我们只需要关心hhh和ttt,因此可以用(hi,ti)(h_i, t_i)(hi,ti)来概括观测数据。
我们的观测数据为(正面次数和反面次数):
| 轮数i | 正面次数hih_ihi | 反面次数tit_iti |
|---|---|---|
| 1 | 5 | 5 |
| 2 | 9 | 1 |
| 3 | 8 | 2 |
| 4 | 1 | 9 |
| 5 | 1 | 9 |
为了直观理解,这里给出每轮可能的序列示例(注意:任何具有相同hih_ihi的序列概率相同,这里只是示例):
- 第1轮(5正5反):正正正正正反反反反反
- 第2轮(9正1反):正正正正正正正正正反
- 第3轮(8正2反):正正正正正正正正反反
- 第4轮(1正9反):正反反反反反反反反反
- 第5轮(1正9反):正反反反反反反反反反
1.2 一次完整的EM迭代
初始化
θA(0)=0.6,θB(0)=0.5 \theta_A^{(0)} = 0.6, \quad \theta_B^{(0)} = 0.5 θA(0)=0.6,θB(0)=0.5
E步:计算隐变量后验分布
对于每一轮iii,计算:
γiA(t)=P(zi=A∣xi,θ(t))=θA(t)hi(1−θA(t))10−hiθA(t)hi(1−θA(t))10−hi+θB(t)hi(1−θB(t))10−hi \gamma_{iA}^{(t)} = P(z_i=A|x_i,\theta^{(t)}) = \frac{\theta_A^{(t)h_i}(1-\theta_A^{(t)})^{10-h_i}}{\theta_A^{(t)h_i}(1-\theta_A^{(t)})^{10-h_i} + \theta_B^{(t)h_i}(1-\theta_B^{(t)})^{10-h_i}} γiA(t)=P(zi=A∣xi,θ(t))=θA(t)hi(1−θA(t))10−hi+θB(t)hi(1−θB(t))10−hiθA(t)hi(1−θA(t))10−hi
(假设先验P(zi=A)=P(zi=B)=0.5P(z_i=A)=P(z_i=B)=0.5P(zi=A)=P(zi=B)=0.5,分子分母同时乘以0.5后约去)
用向量化表示,记θA=θA(t)\theta_A = \theta_A^{(t)}θA=θA(t),θB=θB(t)\theta_B = \theta_B^{(t)}θB=θB(t):
| 轮数i | 计算过程 | γiA(t)\gamma_{iA}^{(t)}γiA(t)结果 |
|---|---|---|
| 1 | 0.65×0.450.65×0.45+0.510\frac{0.6^5 \times 0.4^5}{0.6^5 \times 0.4^5 + 0.5^{10}}0.65×0.45+0.5100.65×0.45 | 0.4487 |
| 2 | 0.69×0.410.69×0.41+0.510\frac{0.6^9 \times 0.4^1}{0.6^9 \times 0.4^1 + 0.5^{10}}0.69×0.41+0.5100.69×0.41 | 0.8053 |
| 3 | 0.68×0.420.68×0.42+0.510\frac{0.6^8 \times 0.4^2}{0.6^8 \times 0.4^2 + 0.5^{10}}0.68×0.42+0.5100.68×0.42 | 0.7334 |
| 4,5 | 0.61×0.490.61×0.49+0.510\frac{0.6^1 \times 0.4^9}{0.6^1 \times 0.4^9 + 0.5^{10}}0.61×0.49+0.5100.61×0.49 | 0.1386 |
同理,γiB(t)=1−γiA(t)\gamma_{iB}^{(t)} = 1 - \gamma_{iA}^{(t)}γiB(t)=1−γiA(t)。
M步:重新估计参数
最大化Q函数:
Q(θ∣θ(t))=∑i=15[γiA(t)log(θAhi(1−θA)10−hi)+γiB(t)log(θBhi(1−θB)10−hi)] Q(\theta|\theta^{(t)}) = \sum_{i=1}^5 \left[ \gamma_{iA}^{(t)} \log(\theta_A^{h_i}(1-\theta_A)^{10-h_i}) + \gamma_{iB}^{(t)} \log(\theta_B^{h_i}(1-\theta_B)^{10-h_i}) \right] Q(θ∣θ(t))=i=1∑5[γiA(t)log(θAhi(1−θA)10−hi)+γiB(t)log(θBhi(1−θB)10−hi)]
对θA\theta_AθA和θB\theta_BθB分别求导并令导数为0,得到闭式解:
θA(t+1)=∑i=15γiA(t)hi10∑i=15γiA(t) \theta_A^{(t+1)} = \frac{\sum_{i=1}^5 \gamma_{iA}^{(t)} h_i}{10 \sum_{i=1}^5 \gamma_{iA}^{(t)}} θA(t+1)=10∑i=15γiA(t)∑i=15γiA(t)hi
θB(t+1)=∑i=15γiB(t)hi10∑i=15γiB(t) \theta_B^{(t+1)} = \frac{\sum_{i=1}^5 \gamma_{iB}^{(t)} h_i}{10 \sum_{i=1}^5 \gamma_{iB}^{(t)}} θB(t+1)=10∑i=15γiB(t)∑i=15γiB(t)hi
代入数值计算:
θA(1)=0.4487×5+0.8053×9+0.7334×8+0.1386×1+0.1386×110×(0.4487+0.8053+0.7334+0.1386+0.1386)=0.6902 \theta_A^{(1)} = \frac{0.4487 \times 5 + 0.8053 \times 9 + 0.7334 \times 8 + 0.1386 \times 1 + 0.1386 \times 1}{10 \times (0.4487 + 0.8053 + 0.7334 + 0.1386 + 0.1386)} = 0.6902 θA(1)=10×(0.4487+0.8053+0.7334+0.1386+0.1386)0.4487×5+0.8053×9+0.7334×8+0.1386×1+0.1386×1=0.6902
θB(1)=0.5513×5+0.1947×9+0.2666×8+0.8614×1+0.8614×110×(0.5513+0.1947+0.2666+0.8614+0.8614)=0.3058 \theta_B^{(1)} = \frac{0.5513 \times 5 + 0.1947 \times 9 + 0.2666 \times 8 + 0.8614 \times 1 + 0.8614 \times 1}{10 \times (0.5513 + 0.1947 + 0.2666 + 0.8614 + 0.8614)} = 0.3058 θB(1)=10×(0.5513+0.1947+0.2666+0.8614+0.8614)0.5513×5+0.1947×9+0.2666×8+0.8614×1+0.8614×1=0.3058
1.3 迭代过程与收敛
| 迭代次数ttt | θA(t)\theta_A^{(t)}θA(t) | θB(t)\theta_B^{(t)}θB(t) |
|---|---|---|
| 0 | 0.6000 | 0.5000 |
| 1 | 0.6902 | 0.3058 |
| 2 | 0.7758 | 0.1891 |
| 3 | 0.8316 | 0.1209 |
| 4 | 0.8567 | 0.0937 |
| 5 | 0.8662 | 0.0827 |
| 10 | ≈0.8687 | ≈0.0789 |
经过约10次迭代,参数基本收敛到:
θA≈0.87,θB≈0.08 \theta_A ≈ 0.87, \quad \theta_B ≈ 0.08 θA≈0.87,θB≈0.08
1.4 结果解释
- 算法成功区分出两枚硬币:一枚高概率(0.87),一枚低概率(0.08)
- 正面次数多的数据(第2、3轮)被分配给硬币A,正面次数少的数据(第4、5轮)被分配给硬币B
- 第1轮(5正5反)最难判断,后验概率接近0.5:0.5
- EM算法通过迭代逐步改进了参数估计,即使从错误的初始猜测开始
二、程序模拟
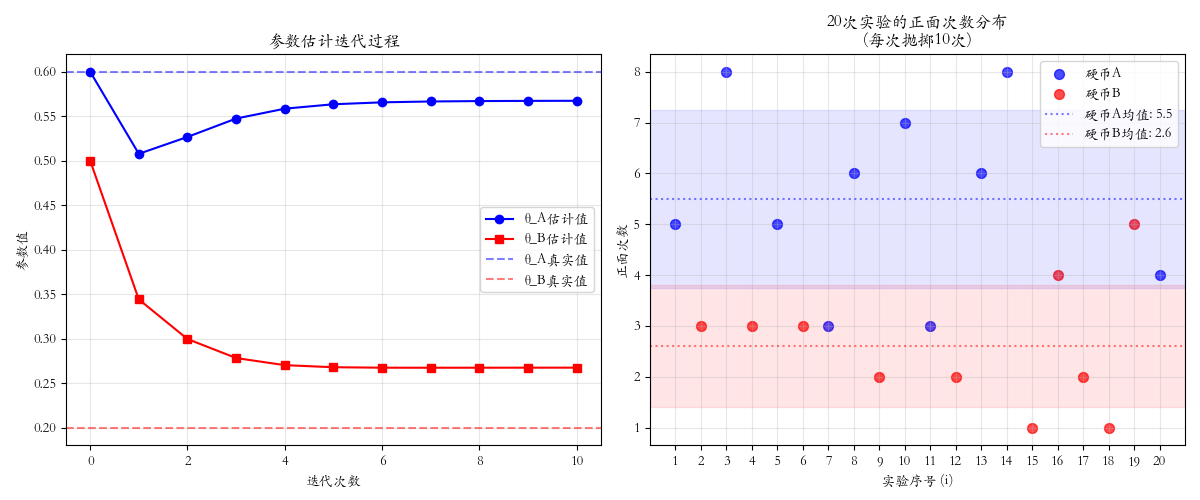
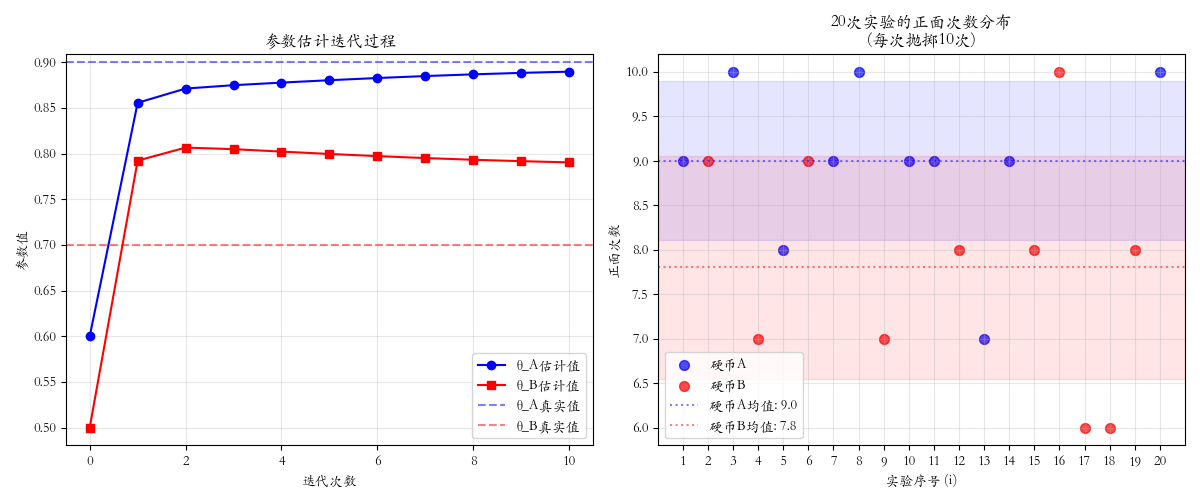
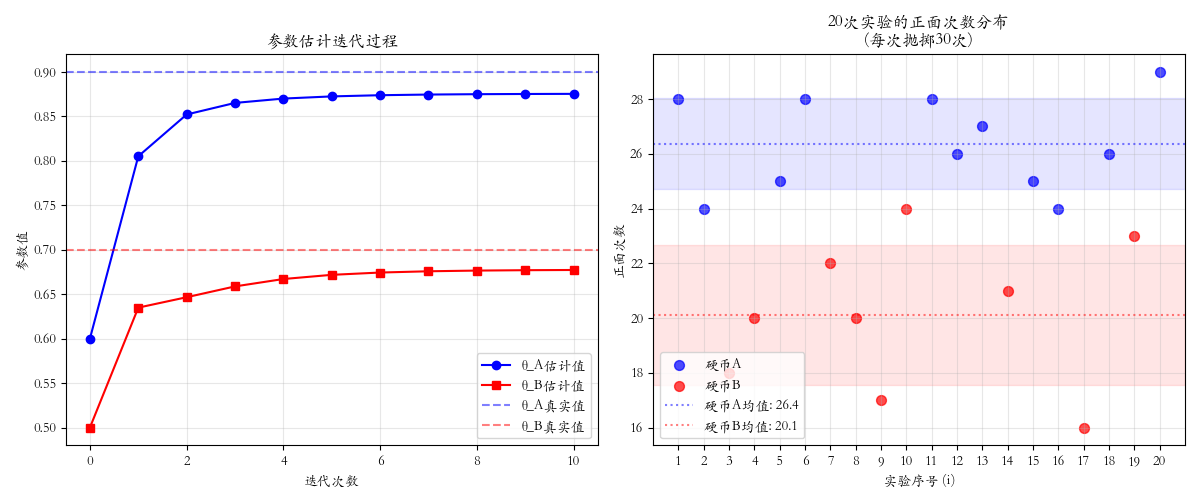
python
import warnings
from typing import List, Tuple, Dict
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
matplotlib.rcParams['axes.unicode_minus'] = False
matplotlib.rcParams['font.family'] = 'Kaiti SC'
warnings.filterwarnings('ignore')
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# ==================== 第一部分:数据模拟 ====================
def simulate_coin_experiments(
theta_A: float = 0.8, # 硬币A的真实正面概率
theta_B: float = 0.3, # 硬币B的真实正面概率
n_experiments: int = 20, # 实验次数
n_tosses: int = 20, # 每次实验抛掷次数
seed: int = 42 # 随机种子
) -> Tuple[List[int], List[str]]:
"""
模拟硬币抛掷实验
参数:
theta_A: 硬币A的正面概率
theta_B: 硬币B的正面概率
n_experiments: 实验次数
n_tosses: 每次实验抛掷次数
seed: 随机种子
返回:
heads_counts: 每次实验的正面次数列表
true_coins: 每次实验真实使用的硬币列表
"""
np.random.seed(seed)
heads_counts = []
true_coins = []
for _ in range(n_experiments):
# 随机选择硬币(假设先验概率各为0.5)
if np.random.random() < 0.5:
true_coin = 'A'
theta = theta_A
else:
true_coin = 'B'
theta = theta_B
# 进行n_tosses次抛掷
tosses = np.random.random(n_tosses) < theta
heads_count = int(np.sum(tosses))
heads_counts.append(heads_count)
true_coins.append(true_coin)
return heads_counts, true_coins
# ==================== 第二部分:EM算法核心 ====================
def compute_posterior(
heads_count: int,
theta_A: float,
theta_B: float,
n_tosses: int = 20
) -> Tuple[float, float]:
"""
计算单次实验的后验概率
参数:
heads_count: 正面次数
theta_A: 硬币A的当前估计概率
theta_B: 硬币B的当前估计概率
n_tosses: 抛掷次数
返回:
gamma_A: 属于硬币A的概率
gamma_B: 属于硬币B的概率
"""
# 计算两种假设下的似然
if theta_A > 0 and theta_A < 1:
likelihood_A = (theta_A ** heads_count) * ((1 - theta_A) ** (n_tosses - heads_count))
else:
likelihood_A = 0
if theta_B > 0 and theta_B < 1:
likelihood_B = (theta_B ** heads_count) * ((1 - theta_B) ** (n_tosses - heads_count))
else:
likelihood_B = 0
# 避免数值下溢
if likelihood_A == 0 and likelihood_B == 0:
likelihood_A = likelihood_B = 1e-10
# 假设先验概率相等,计算后验概率
total = likelihood_A + likelihood_B
if total == 0:
gamma_A = gamma_B = 0.5
else:
gamma_A = likelihood_A / total
gamma_B = likelihood_B / total
return gamma_A, gamma_B
def em_algorithm_for_coins(
heads_counts: List[int],
initial_theta_A: float = 0.6,
initial_theta_B: float = 0.5,
n_tosses: int = 20,
max_iterations: int = 10,
tolerance: float = 1e-6
) -> Dict:
"""
EM算法估计硬币概率
参数:
heads_counts: 每次实验的正面次数列表
initial_theta_A: 硬币A的初始估计
initial_theta_B: 硬币B的初始估计
n_tosses: 每次实验抛掷次数
max_iterations: 最大迭代次数
tolerance: 收敛阈值
返回:
result_dict: 包含所有结果的字典
"""
n_experiments = len(heads_counts)
# 初始化参数
theta_A = initial_theta_A
theta_B = initial_theta_B
# 记录迭代历史
theta_A_history = [theta_A]
theta_B_history = [theta_B]
for iteration in range(max_iterations):
# ========== E步 ==========
# 初始化统计量
weighted_heads_A = 0.0
weighted_heads_B = 0.0
total_weight_A = 0.0
total_weight_B = 0.0
# 计算后验概率并累计统计量
for h in heads_counts:
gamma_A, gamma_B = compute_posterior(h, theta_A, theta_B, n_tosses)
weighted_heads_A += gamma_A * h
weighted_heads_B += gamma_B * h
total_weight_A += gamma_A
total_weight_B += gamma_B
# ========== M步 ==========
# 更新参数
new_theta_A = weighted_heads_A / (total_weight_A * n_tosses) if total_weight_A > 0 else theta_A
new_theta_B = weighted_heads_B / (total_weight_B * n_tosses) if total_weight_B > 0 else theta_B
# 避免参数越界
new_theta_A = max(0.001, min(0.999, new_theta_A))
new_theta_B = max(0.001, min(0.999, new_theta_B))
# 检查收敛
delta_A = abs(new_theta_A - theta_A)
delta_B = abs(new_theta_B - theta_B)
# 更新参数
theta_A = new_theta_A
theta_B = new_theta_B
# 记录历史
theta_A_history.append(theta_A)
theta_B_history.append(theta_B)
# 打印当前迭代信息
print(f"迭代 {iteration + 1}: θ_A = {theta_A:.4f}, θ_B = {theta_B:.4f}")
# 检查收敛
if max(delta_A, delta_B) < tolerance:
print(f"在第{iteration + 1}次迭代后收敛")
break
return {
'theta_A_history': theta_A_history,
'theta_B_history': theta_B_history,
'final_theta_A': theta_A,
'final_theta_B': theta_B,
'n_iterations': len(theta_A_history) - 1
}
# ==================== 快速演示版本 ====================
def quick_demo():
"""快速演示版本"""
print("EM算法快速演示")
print("-" * 40)
# 设置实验参数
true_theta_A = 0.9
true_theta_B = 0.7
n_experiments = 20
n_tosses = 30
print(f"实验设置:")
print(f" - 总实验次数: {n_experiments}")
print(f" - 每次实验抛掷次数: {n_tosses}")
print(f" - 硬币A的真实正面概率: {true_theta_A:.2f}")
print(f" - 硬币B的真实正面概率: {true_theta_B:.2f}")
print()
# 1. 简单模拟数据
np.random.seed(42)
# 生成20个简单数据点
heads_counts, true_coins = simulate_coin_experiments(
theta_A=true_theta_A,
theta_B=true_theta_B,
n_experiments=n_experiments,
n_tosses=n_tosses,
seed=42
)
# 2. 运行EM算法
print(f"每次实验的正面次数: {heads_counts}")
print(f"\nEM算法迭代过程:")
result = em_algorithm_for_coins(
heads_counts=heads_counts,
initial_theta_A=0.6,
initial_theta_B=0.5,
n_tosses=n_tosses,
max_iterations=10
)
print(f"\n最终估计结果:")
print(f" θ_A (估计) = {result['final_theta_A']:.4f} (真实: {true_theta_A:.2f})")
print(f" θ_B (估计) = {result['final_theta_B']:.4f} (真实: {true_theta_B:.2f})")
print(f" 迭代次数: {result['n_iterations']}")
# 3. 计算准确率
correct = 0
for i, h in enumerate(heads_counts):
gamma_A, gamma_B = compute_posterior(h, result['final_theta_A'], result['final_theta_B'])
predicted = 'A' if gamma_A > gamma_B else 'B'
if predicted == true_coins[i]:
correct += 1
accuracy = correct / len(heads_counts) * 100
print(f"硬币分配准确率: {accuracy:.2f}%")
# 4. 简单可视化
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
# 参数迭代
ax[0].plot(result['theta_A_history'], 'b-o', label='θ_A估计值')
ax[0].plot(result['theta_B_history'], 'r-s', label='θ_B估计值')
ax[0].axhline(true_theta_A, color='b', linestyle='--', alpha=0.5, label='θ_A真实值')
ax[0].axhline(true_theta_B, color='r', linestyle='--', alpha=0.5, label='θ_B真实值')
ax[0].set_xlabel('迭代次数')
ax[0].set_ylabel('参数值')
ax[0].set_title('参数估计迭代过程')
ax[0].legend()
ax[0].grid(True, alpha=0.3)
# 正面次数散点图
experiment_numbers = list(range(1, n_experiments + 1))
# 分离硬币A和硬币B的数据
heads_A = []
experiments_A = []
heads_B = []
experiments_B = []
for i, (h, coin) in enumerate(zip(heads_counts, true_coins)):
if coin == 'A':
heads_A.append(h)
experiments_A.append(i + 1)
else:
heads_B.append(h)
experiments_B.append(i + 1)
# 绘制散点图
ax[1].scatter(experiments_A, heads_A, color='blue', s=50, label='硬币A', alpha=0.7)
ax[1].scatter(experiments_B, heads_B, color='red', s=50, label='硬币B', alpha=0.7)
# 添加均值和标准差参考线
if heads_A:
mean_A = np.mean(heads_A)
std_A = np.std(heads_A)
ax[1].axhline(mean_A, color='blue', linestyle=':', alpha=0.5, label=f'硬币A均值: {mean_A:.1f}')
ax[1].fill_between([0, n_experiments + 1],
[mean_A - std_A, mean_A - std_A],
[mean_A + std_A, mean_A + std_A],
color='blue', alpha=0.1)
if heads_B:
mean_B = np.mean(heads_B)
std_B = np.std(heads_B)
ax[1].axhline(mean_B, color='red', linestyle=':', alpha=0.5, label=f'硬币B均值: {mean_B:.1f}')
ax[1].fill_between([0, n_experiments + 1],
[mean_B - std_B, mean_B - std_B],
[mean_B + std_B, mean_B + std_B],
color='red', alpha=0.1)
ax[1].set_xlabel('实验序号 (i)')
ax[1].set_ylabel('正面次数')
ax[1].set_title(f'{n_experiments}次实验的正面次数分布\n(每次抛掷{n_tosses}次)')
ax[1].set_xticks(range(1, n_experiments + 1))
ax[1].legend()
ax[1].grid(True, alpha=0.3)
# 设置x轴范围
ax[1].set_xlim(0, n_experiments + 1)
plt.tight_layout()
plt.show()
# ==================== 运行程序 ====================
if __name__ == "__main__":
quick_demo()