数据结构——栈和队列

1.栈（Stack)

1.1 栈的引出

在工作中，我们会经常使用 word 文档，当有一个格式错误或者误删时，我们第一时间想到的就是撤销返回上一步，如果需要多次撤销，那么撤销的步骤也是从距离格式错误的最近一次开始，也就是说后面写错的最先撤回，第一个错的反而是最后撤回，类似这种先执行，后撤回的行为对应数据结构中的栈（Stack）。

1.2 栈的概念

栈是一种特殊的线性表，它只允许在固定的一端进行插入和删除元素操作 。进行插入和删除元素操作的一端称为栈顶，与之相反的另一端称为栈底。

压栈：栈的插入操作叫做进栈/入栈/压栈：出栈：栈的删除操作叫做出栈 。压栈和出栈都是在栈顶进行，遵循后进先出 （LIFO）的原则。在访问时只能访问栈顶元素，不能从栈底或的中间访问元素。

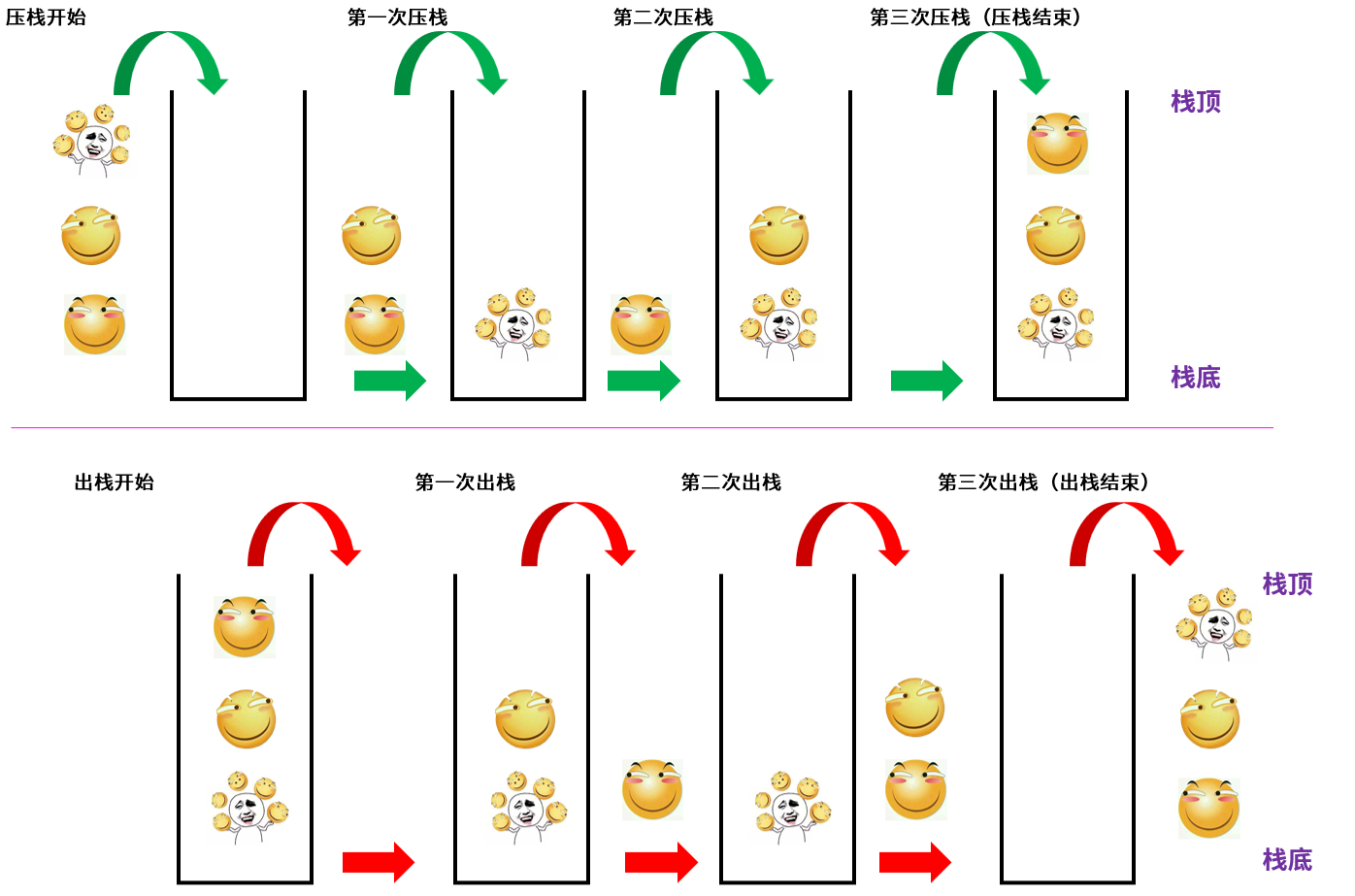
上图是压栈和出栈的简易图理解，在压栈的过程中也可以出栈，并不是只有全部元素入栈后才可以出栈。

1.3 栈的主要方法

栈的主要方法如下：

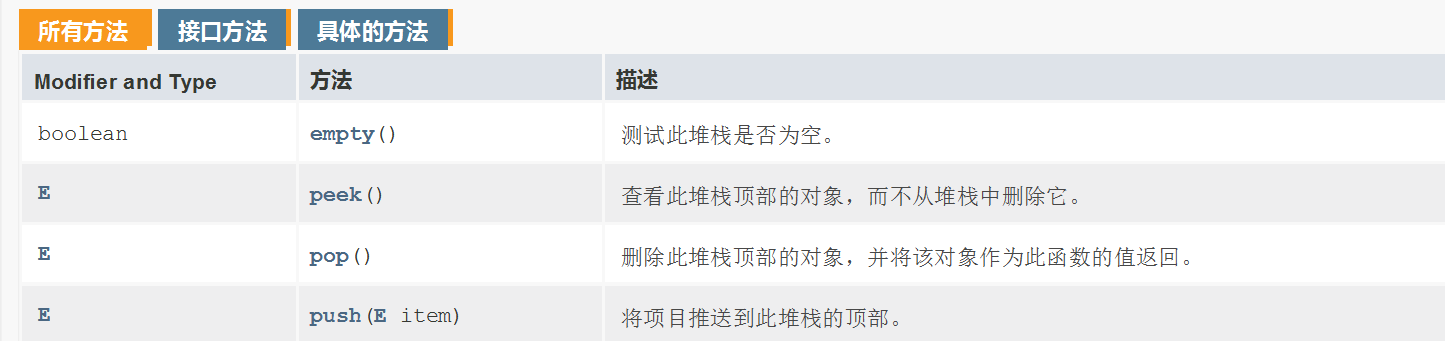
为了更好地理解栈，这里同样对栈的主要方法进行模拟实现，并结合最小栈的问题进行理解。

1.4 栈的模拟实现

实现栈可以用数组，也可以用链表。当栈的最大容量可以预估，或者对于小规模数据需求高性能时，一般使用数组实现栈，而当栈的大小不确定或可能很大，需要频繁的动态增长和收缩等，一般使用链表实现栈。

这里实现链表主要以数组的方式来实现。

java 复制代码

//先做准备工作
public class MyStack {
    public int[] elem;
    public int usedSize;//栈的元素个数
    public MyStack() {
        this.elem = new int[10];//初始定义大小为10
    }
}

1.4.1 empty

方法empty() 是判断栈是否为空 ，返回类型是boolean，如果为空返回 true ，否则返回 false。为空的条件是 usedSize == 0。

java 复制代码

    //判断栈是否为空
    private boolean isEmpty() {
        return usedSize == 0;
    }

1.4.2 push

方法push(int val)是往栈中压入一个元素 ，压入的元素堆在顶部，如果要进行出栈，根据后进先出原则，那么这个元素第一个出。由于是用数组实现，数组所占的空间是有大小的，所有在 push 一个元素时，需要先判断是否已满（方法 isFull()），如果已满，那么需要对这个数组进行扩容，然后在下标 usedSize 插入该元素即可。

java 复制代码

    //压栈
    public void push(int val) {
        if (isFull()) {
            this.elem = Arrays.copyOf(elem , 2 * elem.length);//如果满，以2倍扩容
        }
        this.elem[usedSize] = val;
        this.usedSize++;
    }
    //判满
    private boolean isFull() {
        return usedSize == elem.length;
    }

1.4.3 pop

方法pop()是出栈，即删除栈顶元素 ，并返回这个元素的值，进行这个操作前，要先判断栈是否为空，如果是空，则不能进行出栈操作 ，如果不为空，进行出栈操作后，让栈中的有效元素个数（即 usedSize）减 1。

java 复制代码

    //出栈
    public int pop() {
        //判断栈是否为空
        if (isEmpty()) {
            throw new RuntimeException("栈为空，不能进行出栈操作！！！");
        }
        //栈不为空，获取栈顶元素并返回，同时栈中的有效元素 -1
        int val = elem[usedSize - 1];
        usedSize--;
        return val;
    }

1.4.4 peek

方法peek()是获取栈顶元素，但是不删除，这里需要与上一个方法 pop() 区分开，可以形象记忆为偷偷瞄一眼栈顶元素。同样地，瞄一眼栈顶元素前也可以先对其判断是否为空，如果是空的那就瞄不了了。

java 复制代码

    //获取栈顶元素
    public int peek() {
        if (isEmpty()) {
            throw new EmptyException();
        }
        return elem[usedSize - 1];
    }

1.4.5 size

方法**size()**是获取栈的大小，其大小就是栈的元素个数，也就是这个模拟实现中 usedSize的大小。

java 复制代码

    //栈的大小
    public int size() {
        return usedSize;
    }

1.5 最小栈

最小栈 是一种特殊的栈数据结构，它在支持常规栈操作（push、pop、peek）的同时，还能在 O(1) 时间复杂度内返回栈中的最小元素。

实现实现最小栈，方法包括：

**MinStack()**初始化堆栈对象。

**void push(int val)**将元素 val 推入堆栈。

**void pop()**删除堆栈顶部的元素。

**int top()**获取堆栈顶部的元素。

**int getMin()**获取堆栈中的最小元素。
为什么需要最小栈呢？

普通栈无法直接获取栈的最小值，如果每次调用 pop() 遍历整个栈，对比栈前后的元素值，那么需要遍历整个栈，时间复杂度会是 O(n) ，效率太低。最小栈通过优化存储方式，定义一个 getMin() 方法，使其时间复杂度降为 O(1)，适用于需要频繁查询最小值的场景。

思路提示：

最小栈可以用两个栈来实现，记为一个正常放元素的普通栈，一个放最小元素模拟最小栈，当元素全部全部放入普通栈后，最小栈的栈顶元素就是最小元素。可以看一组数字：0，-1，-2，2，-2，5 将这组数字按顺序压入栈中，即压栈操作的第一个元素是 0 。

重点理解：当最小栈为空或者待压栈元素小于等最小栈栈顶元素时，都要压栈！出栈时，从普通栈中出，当普通栈出栈的元素与最小栈的栈顶元素相等时，最小栈的栈顶元素也出栈！

第一次压栈：先进行普通栈的压栈操作，这个普通栈不论里面存放的元素是多大，都需要压入栈中，然后看最小栈，由于第一次压栈，最小栈中并没有元素（即最小栈为空），所以第一个元素默认是最小栈的最小元素，此时就需要把 0 压入最小栈中；

第二次压栈：第二次压栈的元素是 -1 ，正常压入普通栈，此时对比 -1 这个元素和最小栈的栈顶元素（这里就是和 0 作对比，因为此时栈顶元素是 0 ）这里是对最小栈的栈顶元素瞄一眼，即 peek() ，而不是pop()，由于 -1 比 0 小，继续压入栈中；

第三次压栈：重复上述步骤，普通栈正常入栈，-2 和最小栈栈顶元素对比，-2 小压入栈中；

第四次压栈：普通栈正常入栈，元素 2 比最小栈栈顶元素 -2 大，不压入栈中；

第五次压栈，普通栈正常入栈，元素 -2 和最小栈的栈顶元素是相等的，这个栈是否要压栈呢？答案是要！！为什么呢？因为要确保最小栈的栈顶元素永远是最小值，如果相等的情况不进行压栈，那么在出栈的时候，之前栈顶元素的 -2 就会跟第四个元素 -2 出栈，而在普通栈中还有一个 -2，此时最小栈的栈顶元素已经不是 -2。所以最小栈的压栈条件是要判断待压栈的元素和最小栈的栈顶元素作对比，当小于等于时，就要压栈！！！

第六次压栈：普通栈正常入栈，元素 5 大于最小栈的栈顶元素 -2，不压栈。

java 复制代码

class MinStack {
    Stack<Integer> stack;//普通栈
    Stack<Integer> minStack;//最小栈

    //构造方法
    public MinStack(){
        stack = new Stack<>();
        minStack = new Stack<>();
    }
    //压栈
    public void push(int val){
        //普通栈不管什么元素都要正常压栈
        stack.push(val);
        if(minStack.empty() || val <= minStack.peek()){
            minStack.push(val);
        }
    }
    //出栈
    public void pop(){
        if(stack.empty()){
            return;
        }
        int val = stack.pop();//记录一下普通栈的出栈元素
        if(val == minStack.peek()){
            //如果普通栈出栈元素和最小栈的栈顶元素相等，则最小栈的栈顶元素也出栈
            minStack.pop();
        }
    }
    //获取普通栈的栈顶元素
    public int top(){
        if(stack.empty()){
            throw new IllegalStateException("栈为空，不能获取元素！");
        }
        return stack.peek();
    }
    //获取栈中的最小元素
    public int getMin(){
        if(minStack.empty()){
            throw new IllegalStateException("最小栈为空，不能获取元素！");
        }
        return minStack.peek();
    }
}

1.6 栈、虚拟机栈、栈帧的区别

1. 栈（Stack）

栈是一种线性数据结构，遵循LIFO（后进先出）原则

主要操作：push（压栈）、pop（出栈）、peek（瞄一眼栈顶）

实现方式：可以用数组或链表实现

2. 虚拟机栈（JVM Stack）

是JVM内存模型中的一块线程私有内存区域

生命周期与线程相同，随线程创建而创建，线程结束而销毁

存储栈帧（Stack Frame），用于Java方法执行

3. 栈帧（Stack Frame）

是虚拟机栈的基本组成单元，代表一个方法的执行环境

2.队列(Queue)

2.1 队列的引出

生活中队列的例子随处可见，比如食堂排队打饭，在车站里排队检票，这种情况下先排队的先打饭/检票，类似这种先执行先享受的行为对应数据结构中的队列（Queue）。

2.2 队列的概念

队列也是一种特殊的线性表，它只允许在一端进行数据插入操作，在另一端进行数据删除操作。

进行插入操作（入队）的一端称为队尾 ，进行删除操作（出队）的一端称为队头 。插入和删除遵循先进先出 （FIFO）的原则。在访问时只能访问队头和队尾元素，不能从中间访问元素。

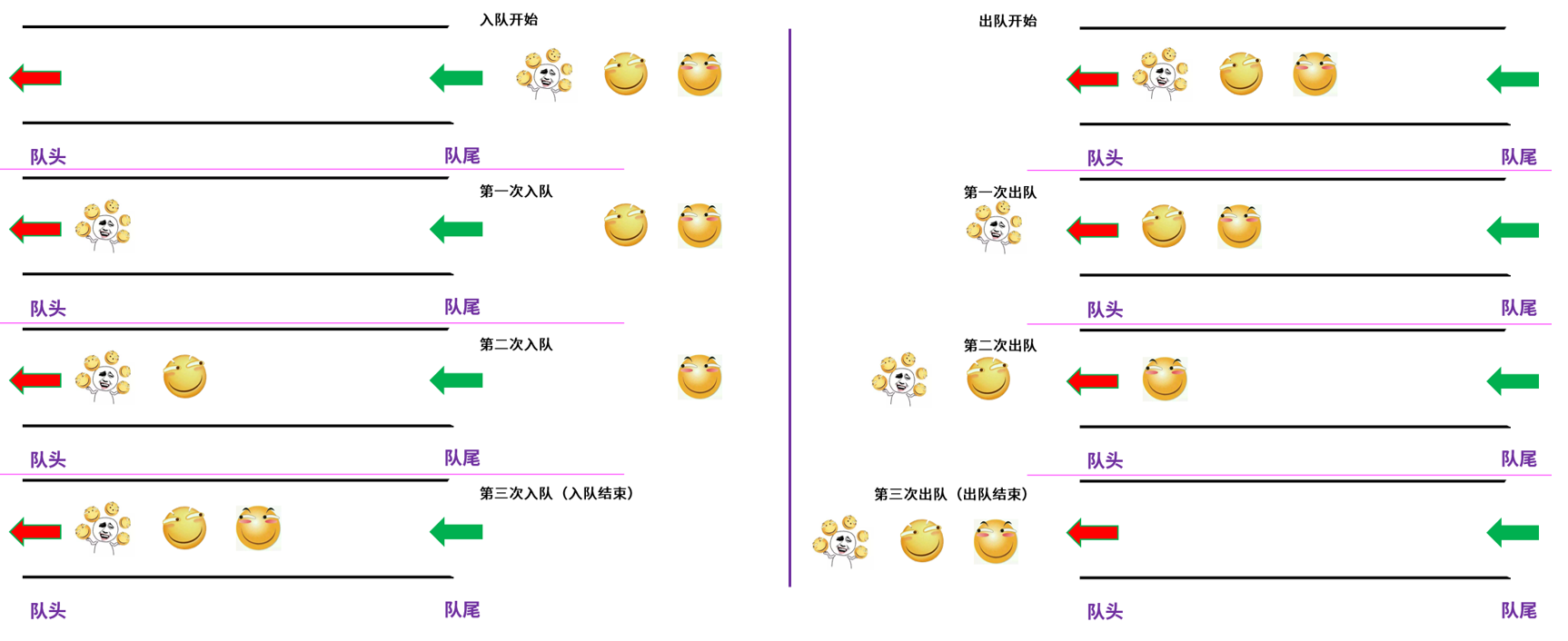
上图是入队和出队的简易图理解，在入队的过程中也可以出队，并不是只有全部元素入队后才可以出队。

2.3 队列的主要方法

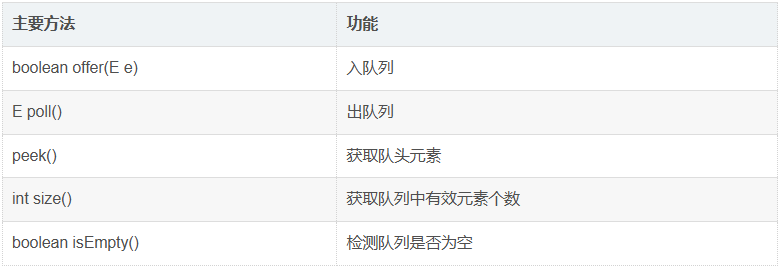
队列的主要方法其实和栈类似，offer和push 都是插入元素 ，poll对应pop 都是弹出元素 ，peek 在队列中是查看队头的元素。

2.4 队列的模拟实现

实现队列可以用数组，也可以用链表。实现队列一般用链表实现，因为对内存的利用都是按需分配，并且扩容成本低，出队入队的效率都是0(1)。链表实现既可以用单向链表，也可以用双向链表。使用单向链表时，每个节点只保存数据和指向下一个节点的指针，入队（offer）在队尾追加新节点，出队（poll），这种方式的缺点是不能反向遍历，也不能从队头入队，如果从队头入队时间复杂度为O(n)；使用双向链表时，每个节点都保存数据和两个指针，分别指向前一个节点和后一个节点，此时队头和队头都可以进行入队和出队的操作，这种也叫双端队列 （Deque）。

这里使用单向的双向链表来实现队列。

java 复制代码

public class MyQueue {
    public static class ListNode{
        public int val;//值
        public ListNode next;//指向下一节点

        public ListNode(int val) {
            this.val = val;
        }
    }
    public ListNode head;//队头
    public ListNode tail;//队尾
    public int usedSize;//队列的大小
}

2.4.1 isEmpty

方法isEmpty() 是判断栈是否为空 ，返回类型是boolean，如果为空返回 true ，否则返回 false。为空的条件是 usedSize == 0。

java 复制代码

    //判空
    public boolean isEmpty() {
        return usedSize == 0;
    }

2.4.2 offer

方法offer(int val)是往队列追加元素，即入队操作 。在追加元素前，要先判断队列是否为空 ，如果是空的，那么队列的队头和队尾都将指向这个新增节点，由于是用链表实现，所有并不需要担心空间已满的问题，在队尾追加元素时，只需要把这个元素接入队尾。

java 复制代码

    //入队
    public void offer(int val){
        ListNode node = new ListNode(val);
        if (isEmpty()) {
            //如果队列为空，队头和队尾都指向这个节点
            head = tail = node;
        } else {
            //如果队头不为空,则从队尾入队
            tail.next = node;
            tail = node;//更新尾节点
        }
        usedSize++;
    }

2.4.3 poll

方法poll()是出队，即删除队头元素 ，并返回该删除的节点。同样地操作，需要先判断队列是否为空，如果是空的，那么就没有出队的必要了，如果不为空，进行出队操作，更新头节点，如果原来的队列只有一个节点，这个时候新的头节点是空的，那么队尾也需要置空。

java 复制代码

    //出队
    public int poll() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空，无法出队！！！");
        }
        int val = head.val;//队头元素的值
        head = head.next;//更新队头
        if (head == null) {
            tail = null;//如果队头为空，那么队尾也要置为空，比如队列只有一个节点时，这个节点出队后，整个队列都是空的
        }
        usedSize--;
        return val;//返回出队元素的值
    }

2.4.4 peek

方法peek()是获取队头元素，但是不删除，这里需要与上一个方法 ppoll() 区分开，可以形象记忆为偷偷瞄一眼队头元素。同样地，瞄一眼队头元素前也可以先对其判断是否为空，如果是空的那就瞄不了了。

java 复制代码

    //获取队头元素的值
    public int peek() {
        if (isEmpty()) {
            throw new RuntimeException("队列为空，不能获取队头元素！！！");
        }
        return head.val;
    }

2.4.5 size

方法**size()**是获取队列的大小，其大小就是队列的元素个数，也就是这个模拟实现中 usedSize的大小。

java 复制代码

    //队列大小
    public int size() {
        return usedSize;
    }

2.5 循环队列(Circular Queue)

在上面的入队和出队操作中，通过画图理解，会发现：入队操作会导致 tail 指针后移，出队操作会导致 headt指针后移，如果想要循环利用一个空间，那么就需要循环队列。

循环队列 （Circular Queue）是一种特殊的线性数据结构，它使用固定大小的数组实现队列，并通过"循环使用"数组空间的方式提高存储效率。

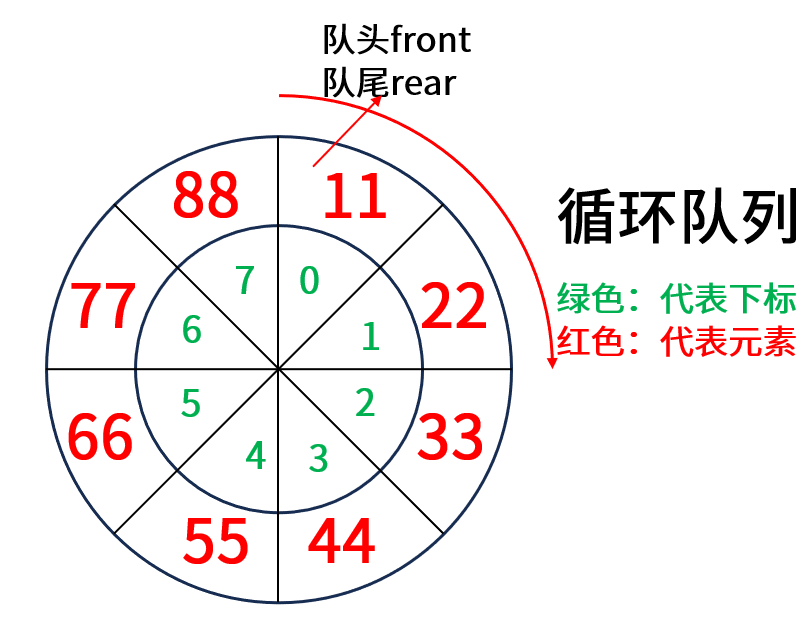
从这个图可以看出一个核心的问题：循环队列是满的，这是肉眼就可以观察的，但是交给程序判断的时候，怎么判断这个循环队列是否已满呢？

变量计数：循环队列是用数组实现的，而数组的大小初始的给定的，假设为 capacity，可以定义一个 size 变量来记录当前元素的数量，所有当元素占满数组时，即 size == capacity 就可以认为该循环队列已满。

标志位：既然是循环队列，那么最开始时，队头和队尾一定在同一个下标，此时队列全部为空，可以定义一个 boolean 类型元素标志为空，当队列开始插入元素后，队尾不断后移，队尾和队头再次相遇时，就可以认为该循环队列已满。

牺牲一个单元存储 ：这种方法是最经典的，它故意浪费一个数组位置，比如在下面的图中，当插完 77 这个元素后，队尾来到了 8 下标的位置，此时进行判断下一个位置是不是队头，如果是队头，那么就可以认为该循环队列已满，不再插入元素。任何定义这个判断是否已满呢？假设数组大小为 capacity，队尾的下标 rear 是肯定是小于 capacity，那么满的条件就是（rear + 1） % capacity == front。

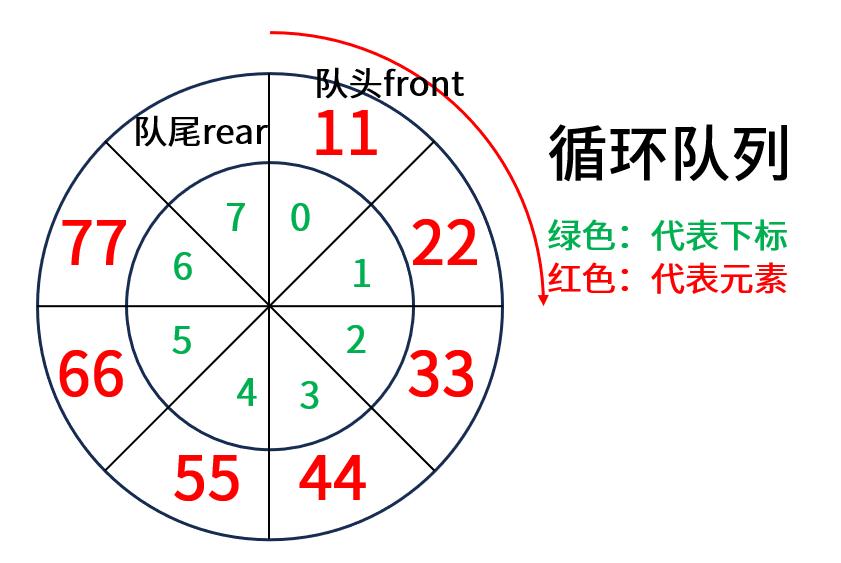
java 复制代码

public class MyCircularQueue {
    public int front;//队头
    public int rear;//队尾
    public int[] elem;

    public MyCircularQueue(int k) {
        this.elem = new int[k + 1];//  多分配一个空间用于判断满状态
    }
    //入队列
    public boolean enQueue(int value) {
        //如果满，不能再加
        if (isFull()) {
            return false;
        }
        elem[rear] = value;
        rear = (rear + 1) % elem.length;
        return true;
    }
    //出队列
    public boolean deQueue() {
        if (isEmpty()) {
            return false;
        }
        front = (front + 1) % elem.length;
        return true;
    }
    //得队头元素
    public int front() {
        if (isEmpty()) {
            return - 1;
        }
        int val = elem[front];
        return val;
    }
    //得队尾元素
    public int rear() {
        if (isEmpty()) {
            return - 1;
        }
        int index = (rear == 0) ? elem.length - 1 : rear - 1;
        //这里需要注意，因为每次插入一个元素后，队尾指针rear都已经后移，此时要获得队尾元素，那么就要 rear - 1
        //但是当rear的位置刚好在0下标时，说明队尾元素是在本篇文章示例图下标 7 的位置，此时只需数组大小 - 1 即可
        int val = elem[index];
        return val;
    }
    //判断是否为空
    public boolean isEmpty() {
        return front == rear;
    }
    //判断是否已满
    public boolean isFull() {
        return (rear + 1) % elem.length == front;
    }
}

2.6 双端队列(Deque)

双端队列(Deque) 是指允许队头和队尾都可以进行入队和出队操作的队列，既可以作为先进先出(FIFO)的队列使用，也可以作为后进先出(LIFO)的栈使用。

双端队列的模拟实现通常用双向链表实现。使用双向链表时，和普通队列的实现相比，多一个前驱的指针域 prev，结合双向链表的实现和普通队列的实现即可。
双端队列 (Deque)是一个接口，不能对其进行实例化，在使用时，必须创建 LinkedList 或者 ArrayDeque 的对象。

Deque<Integer> queue1 = new LinkedList<>();//双端队列的链式实现

Deque<Integer> queue2 = new ArrayDeque<>();//双端队列的线性实现

3.小结

栈和队列都是一种特殊的线性表 。栈遵循后进先出的原则 ，只能在栈顶插入和删除操作，队列遵循先进先出的原则 ，普通队列只能在队尾插入在队头删除，而双端队列的队头和队尾都支持插入和删除操作。栈通常用顺序存储结构方式存储 ，因为数组的尾插效率高，而队列通常用链式结构方式存储，普通队列既可以用单向链表也可以用双向链表实现，循环队列用数组实现，并通常用牺牲一个单元存储来判断队列是否已满，双端队列通常用双向链表实现。