每次打开导航的，导航软件在一秒内给出一个最速路线的时候，你有没有好奇过它是怎么找到这条路的？
假如不考虑堵车、红绿灯等交通影响因素，仅找到一条最短最快的路线，那不论如何也逃不掉 Dijkstra 算法。
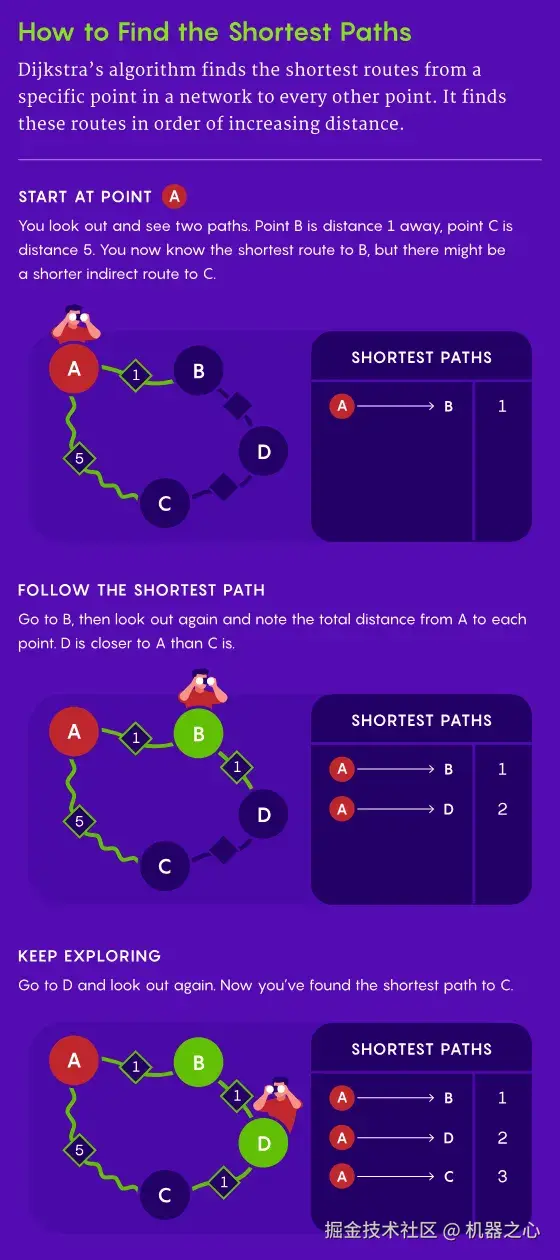
按照传统的 Dijkstra 算法，你将在整段路程中停下多次，寻找每一段的最短路径，然后再去更新下一段如何最短，直到走到目的地。在抉择的过程中会面临着不断选择「最短」路径的情形，还需要通过对比排序来决策。
Dijkstra 算法有多经典呢？
可以说每一个学计算机的学生，甚至每一个学编程理论或数据结构的人，都会在教科书上看到这个算法。
其在计算机学生心中地位甚至不亚于物理学中的基本定律，想到路径最短，必然想到 Dijkstra。
不过，现在有种方法能直接让你跳过不必要的排序，只专注于最重要的点之间的最短距离，大大缩短了所需要的计算时间。这就是清华交叉信息研究院段然团队一项重磅研究给出的全新解法。这项研究还在理论计算机国际顶级会议 STOC 2025 上获得最佳论文奖。
该算法改进了图灵奖得主 Robert Tarjan 等人在 1984 年提出的 O(m + nlogn)算法，后者将 Dijkstra 最短路径算法逼近了理论极限，但并没有完全消除排序的复杂度影响。
-
论文标题：Breaking the Sorting Barrier for Directed Single-Source Shortest
我们先一起回顾一下 Dijkstra 算法。这个最著名的最短路径算法，由荷兰计算机科学家艾兹赫尔・戴克斯特拉于 1956 年提出。 自此，它成为了计算机科学领域的经典，广泛应用于网络路由、地图导航等各个领域。 Dijkstra 算法的目标是找到从一个源点到图中所有其他节点的最短路径。它的基本思路是通过不断选择当前最短的节点，并更新与之相邻的节点的距离，直到所有节点的最短路径都被找到。
去年这个经典算法达到了前所未有的新高度。这篇 FOCS 2024 的最佳论文证明：若我们把任务定义为距离排序问题，在合适的堆结构下，Dijkstra 在排序意义上是普适最优的；也就是说，一旦强制输出排序，就别指望整体复杂度再降了。
-
论文标题： Universal Optimality of Dijkstra via Beyond-Worst-Case Heaps
本次 STOC 最佳论文与之形成互补：避免排序→突破运行时间。他们关注距离的计算，而不关心顶点的具体顺序。它通过分层递归的方式，对图中的节点进行分组处理，并且只对关键节点进行细致的最短路径计算。这样的设计避免了传统 Dijkstra 算法中每次都需要排序的步骤，从而大幅度降低了计算的复杂度。
这个想法早在 2023 年就已经有了雏形。毛啸在加利福尼亚的一次会议上听到了段然关于无向图算法的演讲，双方因此展开了对话。毛啸一直仰慕段然的工作，第一次与他面对面交流时激动不已。
会后，毛啸开始在空闲时间思考这一算法，而段然的团队则在尝试将已有的算法扩展到有向图领域。受 Bellman-Ford 算法启发，尽管这个算法比 Dijkstra 算法慢得多段然团队通过将其分步执行来避免慢速问题，并利用它提前发现关键节点。
2024 年 3 月，毛啸提出了一种无需随机性的解决方案，随后加入段然团队。他们经过几个月的合作，结合彼此的想法，并借用段然 2018 年提出的突破性技巧，最终设计出一种新算法。该算法通过分层方式，像 Dijkstra 一样从源点扩展，但利用 Bellman-Ford 算法识别关键节点，避免了排序瓶颈，比 Dijkstra 更高效。
他们是怎么做到的
在这项研究中，团队给出了一种在具有实数非负边权的有向图上的单源最短路径（SSSP）的确定性 O (mlog2/3n) 时间算法，在比较加法模型中。这是首次打破 Dijkstra 算法在稀疏图上的 O (m+nlogn) 时间界限的结果，表明 Dijkstra 算法不是 SSSP 的最佳选择。
经典的 Dijkstra 算法 Dij（59），结合 Fibonacci 堆 FT（87）或松弛堆 DGST（88）等高级数据结构，可以在 O (m + n log n) 时间内求解单源最短路径（SSSP）问题。该算法在比较 - 加法模型（comparison-addition model）下工作，这种模型适用于实数权重的输入，限制算法只能对边权进行比较和加法运算，并且每个操作的耗时为单位时间。
对于无向图，Pettie 和 Ramachandran（PR，2005）提出了一种基于层次结构的算法，在比较 - 加法模型下可在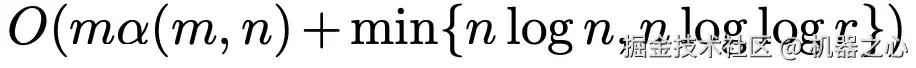 
时间内运行，其中 α 为反 Ackermann 函数，r 为任意两条边权之比的上界。
Dijkstra 算法还会在求解过程中额外生成按源点距离排序的顶点序列。最新研究表明，如果要求算法输出按距离排序的顶点顺序，那么 Dijkstra 算法是最优的。若只需输出顶点距离而不要求顺序，段然、毛啸团队曾提出了一种适用于无向图的随机化 SSSP 算法，其时间复杂度为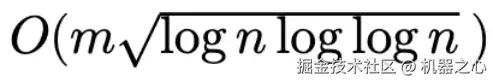 
，在稀疏图中优于 O (n log n) 的结果。然而，对于有向图，这类排序瓶颈依然没有被突破。
定理
存在一种确定性算法，可以在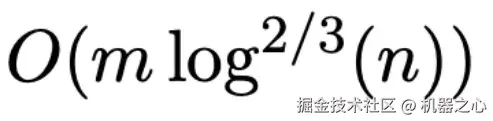 
时间内求解具有实数非负边权的有向图单源最短路径问题。
研究的结果也是第一个在无向图情形下打破 O (m + n log n) 时间界的确定性算法。
技术概述
总的来说，解决单源最短路径问题有两种传统算法：
-
Dijkstra 算法：通过优先队列，每次提取距离源点最近的顶点 u，并从该顶点松弛其所有出边。该方法通常会根据顶点到源点的距离进行排序，因此时间复杂度至少为 Θ(n log n)。
-
Bellman-Ford 算法：基于动态规划思想，多次松弛所有边。若要求解最多包含 k 条边的最短路径，Bellman-Ford 算法无需排序即可在 O (mk) 时间内完成。
段然团队的方法结合了这两种思路，并采用递归划分技术，这种技术类似于瓶颈路径算法。
在 Dijkstra 算法执行过程中的任意时刻，优先队列（堆）都会维护一个前沿（frontier）集合 S，其中包含一些顶点。
如果某个顶点 u 是「未完成的」（即当前的距离估计 d̂u 仍大于真实距离 d (u)），那么从源点 s 到 u 的最短路径必须经过某个已完成的顶点 v∈S。在这种情况下，我们称 u 依赖于 S 中的某个顶点 v。不过集合 S 中的顶点并不保证全部都是已完成的。
Dijkstra 算法会选择 S 中距离源点最近的顶点（它必定是已完成的），然后松弛从该顶点出发的所有边。
运行时间的瓶颈在于：有时前沿集合可能包含 Θ(n) 个顶点。由于需要不断选出距离源点最近的顶点，这意味着必须维护这些顶点的全局有序性，因此无法突破 Ω(n log n) 的排序下界。
核心思想是缩小前沿集合的规模。假设我们只想计算距离小于某个上界 B 的所有顶点的最短路径。令 Ũ 表示所有满足 d (u) < B 且从 s 到 u 的最短路径会经过集合 S 中某个顶点的顶点集合。
可以将前沿的大小 |S| 控制在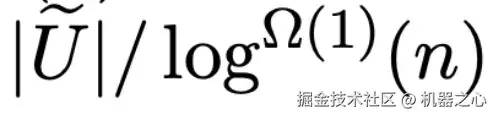 
，也就是「感兴趣的顶点数」的
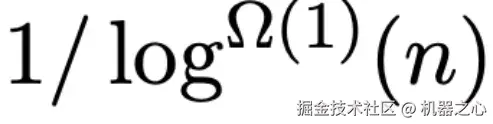倍。
设参数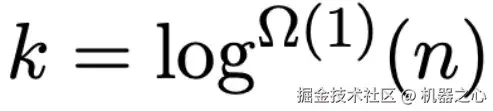 
，有两种情况：
-
如果 |Ũ| > k・|S|，那么前沿大小已经是 |Ũ| /k；
-
否则，若 |Ũ| ≤ k・|S|，则从 S 中的顶点运行 Bellman-Ford 步骤 k 次，所有最短路径中包含少于 k 个 Ũ 顶点的 u∈Ũ 都会被标记为完成状态。否则，若 u 所依赖的 S 中顶点 v 的最短路径树（SPT）中含有不少于 k 个 Ũ 顶点，那么可以将前沿 S 缩减为这些 "枢纽点（pivot）"，且这样的枢纽点数量最多为 |Ũ| /k。
算法基于以上思想，但与传统 Dijkstra 类似的动态前沿方式不同，研究团队采用分治（divide-and-conquer）方案：算法分为 log n /t 层，每层包含一组前沿顶点和一个上界 B。在朴素实现中，每个前沿顶点都需要花费 Θ(t) 时间处理，因此整体仍是每个顶点 Θ(log n) 的开销。
通过在每一层应用前沿缩减策略，我们只需对这些枢纽点（约为前沿顶点的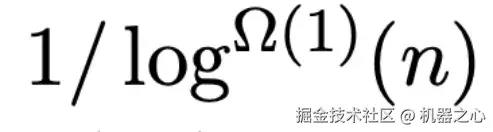
）执行 Θ(t) 操作。这样，每个顶点的处理时间就降低为 
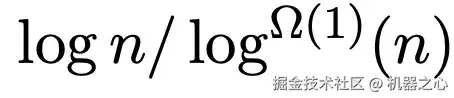，实现显著加速。
算法
该团队研究的是常数度图中从源点 s 出发的单源最短路径问题，且 m = O (n)。在算法中，他们设两个参数：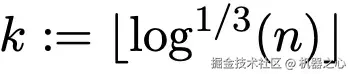
，
。
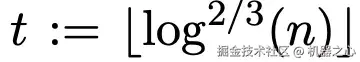他们的核心思想是基于顶点集的分治。我们希望将一个顶点集 U 划分为 2^t 个大小相近的部分：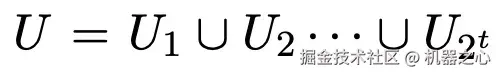
。
其中越靠前的子集中的顶点距离越小，然后递归地继续划分每个 U_i。这样，经过大约 (log n) /t 层递归后，子问题规模将缩小到单个顶点。
为了动态构造这种结构，他们每次尝试计算一批最接近的顶点的距离（不必完全恢复它们的精确距离顺序），并给出一个边界值，表示实际推进了多少。
假设在算法的某个阶段，对于所有 d (u) < b 的顶点 u，它们都已完成，并且团队已经松弛了从它们出发的所有边。此时他们想要找到所有 d (v) ≥ b 顶点的真实距离。
为了避免优先队列中每个顶点 Θ(log n) 的时间开销，他们考虑一个前沿集 S，其中包含所有当前满足 b ≤ d^(v) < B 的顶点（这里 B 是某个上界，并且不对它们进行排序）。可以发现，对于任意未完成顶点 v' 且 b ≤ d (v') < B，它的最短路径一定会经过某个已完成的顶点 u ∈ S。
因此，要计算所有 b ≤ d (v') < B 顶点的真实距离，只需找到从 S 中的顶点出发、距离受限于 B 的最短路径。他们将这个子问题称为有界多源最短路径（Bounded Multi-Source Shortest Path，BMSSP），并为其设计了一个高效算法。
算法 1 查找关键枢纽点
算法 2 BMSSP 的基本情形
算法 3 有界多源最短路径
更多引理及证明、算法细节以及观察结论请参照原论文。
参考链接：