目录
前言
C++中STL的map与set容器广泛应用于实践过程中,本文将详细分析容器最基础的二叉搜索树结构,为后续map与set容器的学习打下更好基础。更多C++内容可前往->|C++主题专栏|<-
1.二叉搜索树的概念
1.1基本结构
二叉搜索树是一种便于快速查找(搜索)数据的搜索结构,也称二叉排序树。它或是棵空树,又或是满足以下性质的树:
二叉搜索树的性质
• 若它的左⼦树不为空,则左⼦树上所有结点的值都⼩于等于根结点的值
• 若它的右⼦树不为空,则右⼦树上所有结点的值都⼤于等于根结点的值
• 它的左右⼦树也分别为⼆叉搜索树
• ⼆叉搜索树中可以⽀持插⼊相等的值,也可以不⽀持插⼊相等的值,具体看使⽤场景定义
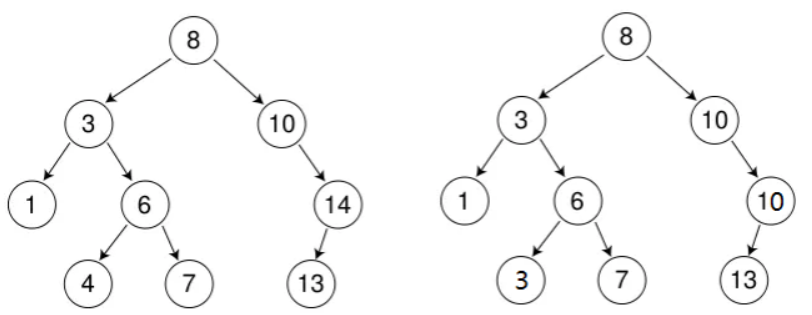
如上两棵树都是二叉搜索树,当然第二棵树的重复元素(10)可以在父节点的左子树也可以在父节点的右子树。但我们常用的一般是左边无重复元素的二叉搜索树。
1.2性能分析
以上面第一棵树为例:这种情况下的树基本为完全二叉树,其搜索性能(时间复杂度)与树的高度相同为logN。但这是最优的情况,若二叉搜索树的数据插入满足一定条件,就会形成类似单支树的情况(如下图),这种情况下的搜索性能就会降为O(N)。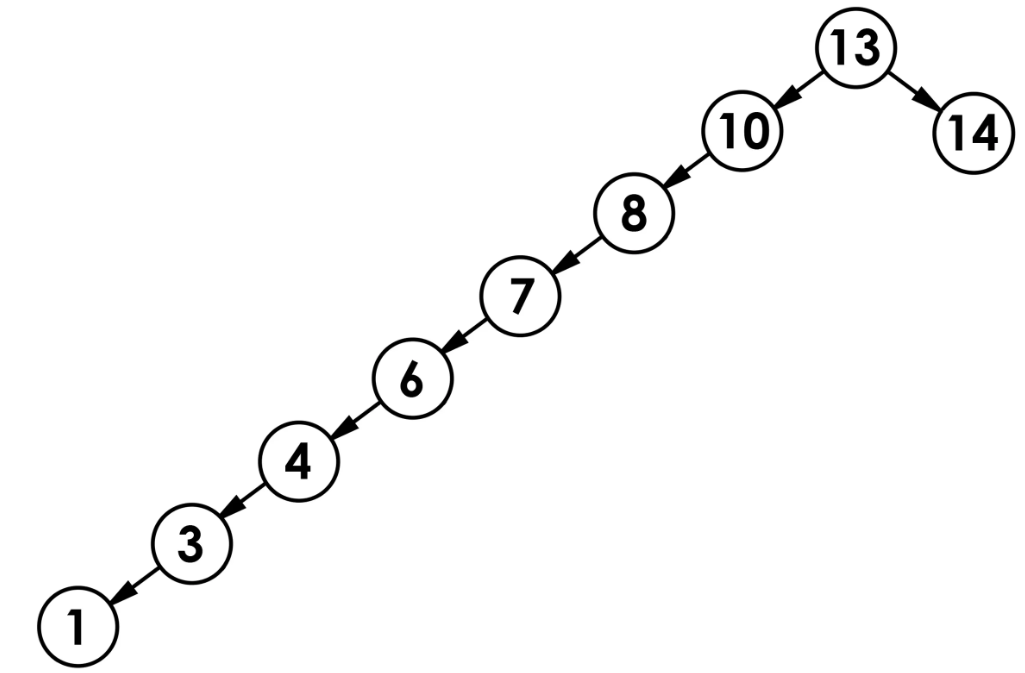
因此综合考虑,普通搜索二叉树的搜索性能就是O(N),但这样的效率显然不够理想,后面在实际应用时使用的是优化过平衡二叉树(AVL树、红黑树)。
其次对于查找功能,在数组中的二分查找算法也能实现O(logN)级别的查找效率,但二分查找算法对比于二叉搜索树有着明显的缺点:
二分查找的缺点
需要存储在⽀持下标随机访问的结构中,并且有序
插⼊和删除数据效率很低。存储在下标随机访问的结构中,插⼊和删除数据⼀般需要挪动数据
这里二叉搜索树的价值也更为显著。
2.二叉搜索树的实现
二叉搜索树的核心功能是增、删、查功能的实现,修改数据值的话主要会破坏搜索结构,进而大大降低效率,因此一般不会实现。下面会从逻辑->代码依次实现各部分功能。
2.1创建
二叉搜索的底层结构还是一个链式二叉树,因此需要结点,主体部分用根来连接各个结点即可。结点中需要储存数据,以及左右孩子结点。但要注意的是搜索结构中显示进行搜索的数据我们一般称为关键字(key)。
其次结点的构造函数只需保证让key值的构造,左右孩子指针置空即可。代码如下:
cpp
#pragma once
#include<iostream>
using namespace std;
//树结点
template<class K>
struct BSTNode
{
K _key;
BSTNode<K>* _left;
BSTNode<K>* _right;
BSTNode(K x)
:_key(x)
,_left(nullptr)
,_right(nullptr)
{}
};
//二叉搜索树
template<class K>
class BSTree
{
private:
typedef BSTNode<K> Node
public:
private:
Node* _root = nullptr;
};2.2插入
插入分为为空插入与非空插入。当树为空的时候只需让根结点指向新结点即可。
当树非空时,按照二叉搜索树的性质,插入值比当前结点大就往右子树走,插入值比当前结点小就往左子树走。
当遇见插入值与当前结点相同时就可以直接返回,表示结构中已有此值。但为了区分void返回的插入成功与失败,我们插入函数的返回类似设置为bool。
以在下图树中插入5为例:
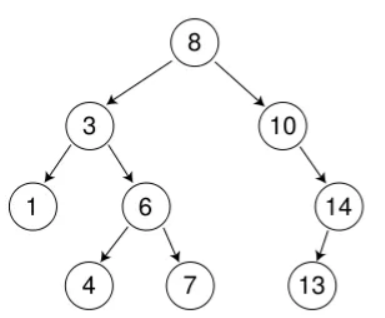
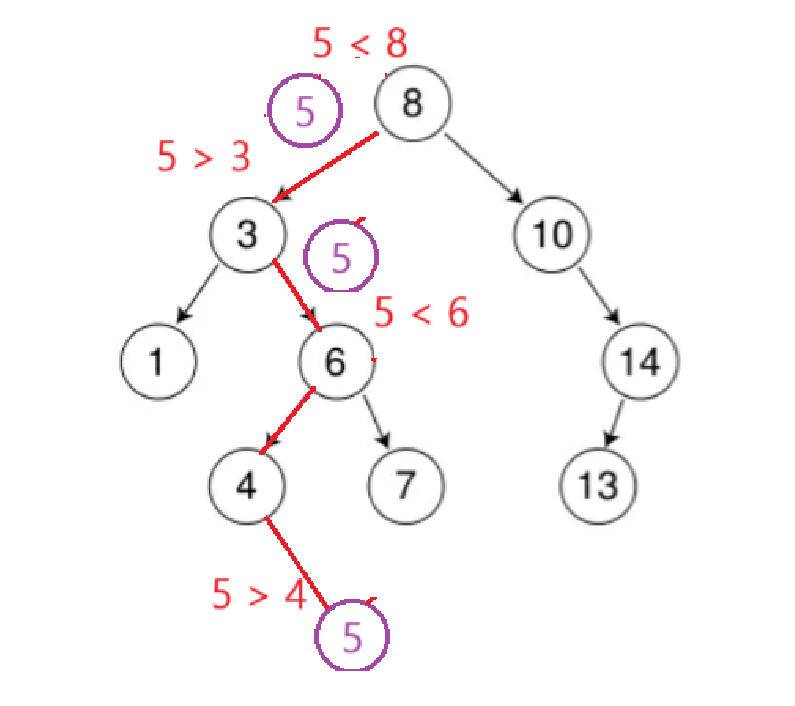
这里最需要注意的是最后一部得到5应该插入的位置时,那个位置是为空的,因此需要在过程中记录应该插入位置的父结点。代码如下:
cpp
//插入
bool insert(const K& key)
{
//分为根为空或不为空
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//不为空则寻找合适位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else if(key == cur->_key)
{
return false; //不插入重复数据
}
}
//插入左还是右
if (key > parent->_key)
{
parent->_right = new Node(key);
}
else
{
parent->_left = new Node(key);
}
return true;
}除了迭代的方式插入,也可通过递归进行插入:
cpp
private:
//递归插入
bool _insert(Node*& root, const K& x)
{
if (root == nullptr)
{
root = new Node(x);
return true;
}
if (root->_key == x)
{
return false;
}
return root->_key > x ? _insert(root->_left, x) : _insert(root->_right, x);
}
public:
//递归插入
bool REinsert(const K& x)
{
return _insert(_root, x);
}这里最值得注意的是递归插入利用引用特性,能直接修改最后空位置的结点。
2.3查找与遍历
二叉搜索树的查找逻辑与插入类似,不同的是遇见相同的值就返回当前结点,若树遍历完没找到就返回空。但查找的前提是树不为空。
二叉搜索树的遍历主要实现方式为中序遍历,这部分主要注意的是在类中显示成员函数实现递归,后面代码实现后再进行分析。
cpp
private:
//方便函数内部传参
void _inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_inorder(root->_left);
cout << root->_key << ' ';
_inorder(root->_right);
}
public:
//遍历------中序遍历
void inorder()
{
_inorder(_root);
cout << endl;
}
//查找
Node* find(const K& x)
{
assert(_root != nullptr);
Node* cur = _root;
while (cur)
{
if (cur->_key < x)
{
cur = cur->_right;
}
else if (cur->_key > x)
{
cur = cur->_left;
}
else if(cur->_key == x)
{
return cur;
}
}
return nullptr;
}递归调用时因要传参数,而在类外部无法直接传树的根结点,因此可以直接在类中进行内部函数嵌套,进而实现递归调用。
2.4删除
二叉搜索树的删除是最复杂的,因为当结点删除时可能也会涉及搜索结构的破坏,但这里的破坏情况会比修改简单。
具体删除情况可以分为以下三种(均以下图树为例):
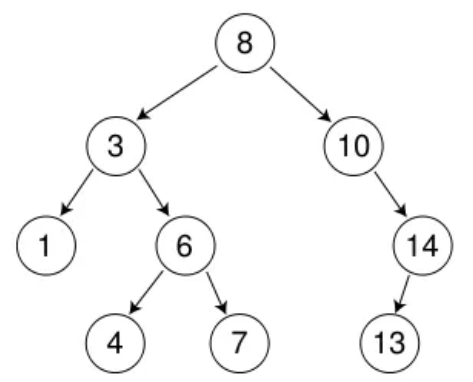
1.要删除结点N左右孩⼦均为空。这时可以直接将改结点删除,并将父节点置为空。
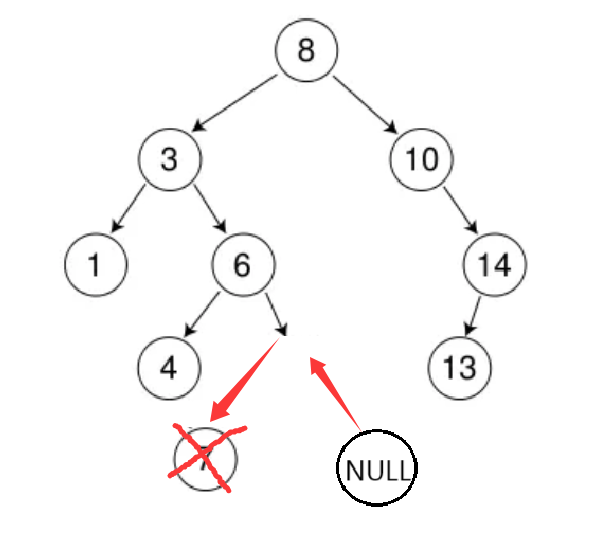
2.要删除的结点N左孩⼦或右孩子为空,另一孩子结点不为空。这种情况下要删改结点,可以直接让该结点的父亲指向该结点的孩子结点。
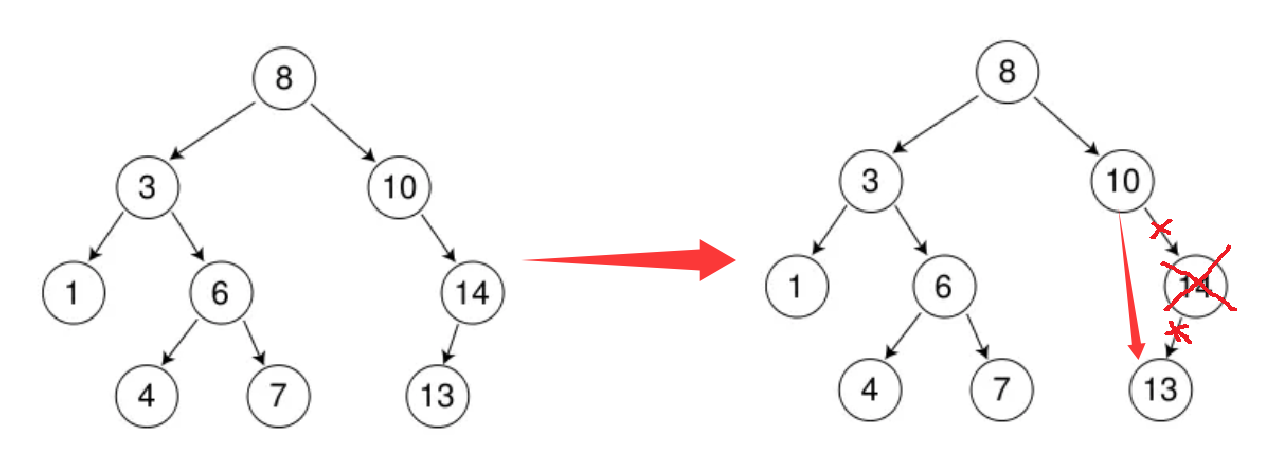
3.要删除的结点N左右孩⼦结点均不为空。这种情况⽆法直接删除N结点,因为N的两个孩⼦⽆处安放,只能⽤替换法删除。找N左⼦树的值最⼤结点R(最右结点)或者N右⼦树的值最⼩结点R(最左结点)替代N,因为这两个结点中任意⼀个,放到N的位置,都满⾜⼆叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换,转⽽变成删除R结点,R结点符合情况2或情况3,可以直接删除。
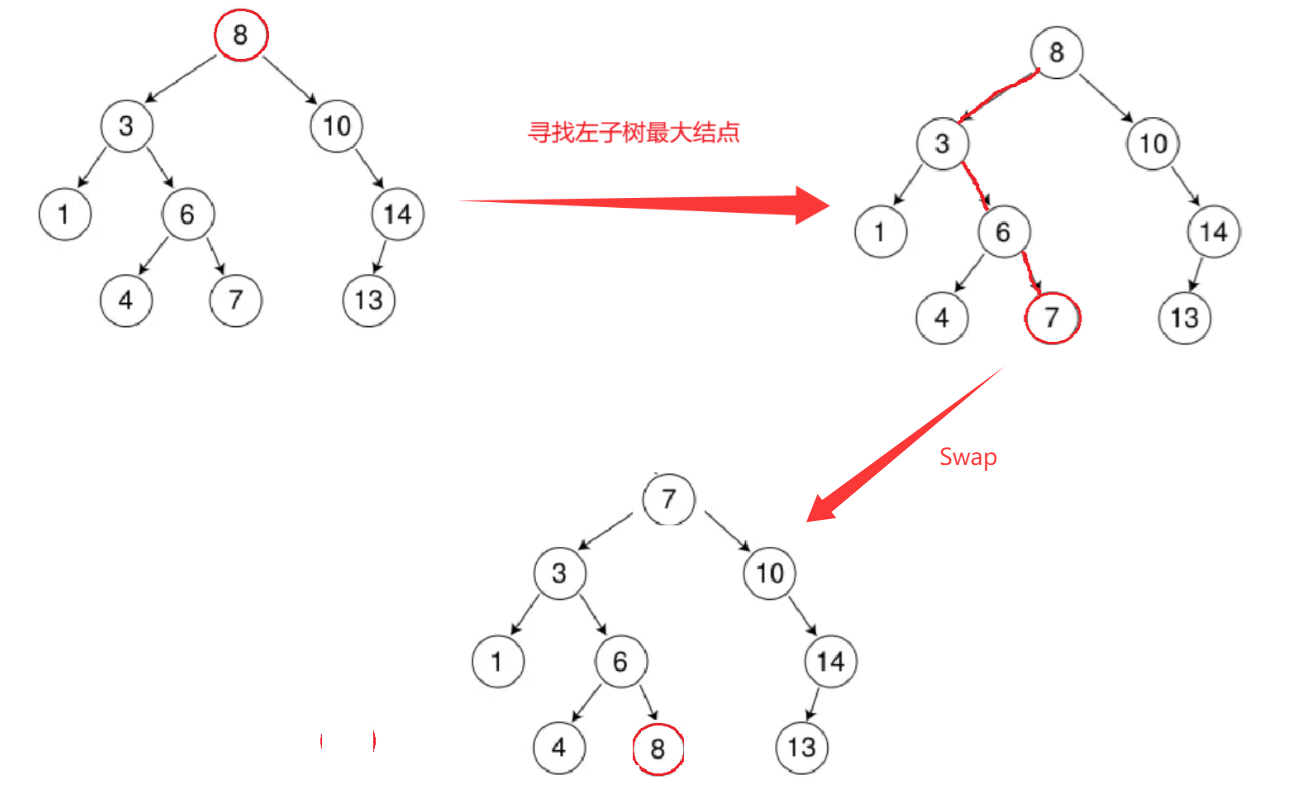
可以看到这里本质是让其变为第一种情况再进行删除。
综上进行代码实现:
cpp
public:
//删除
bool erase(const K& x)
{
//内部查找
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (cur->_key < x)
{
cur = cur->_right;
}
else if (cur->_key > x)
{
cur = cur->_left;
}
else //找到了,进行分情况删除
{
if(cur->_left == nullptr) //左孩子为空
{
if (cur != _root)
{
//父亲指向不为空的右
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else
{
_root = cur->_right;
}
delete cur;
}
else if(cur->_right == nullptr) //右孩子为空
{
if (cur != _root)
{
//父亲指向不为空的右
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
_root = cur->_left;
}
delete cur;
}
else //左右都不为空
{
//查找合适结点------左子树最大
Node* curLeftmax = cur->_left;
Node* maxParent = cur;
while (curLeftmax->_right)
{
maxParent = curLeftmax;
curLeftmax = curLeftmax->_right;
}
//交换key值
swap(cur->_key, curLeftmax->_key);
if (curLeftmax == maxParent->_left)
maxParent->_left = curLeftmax->_right;
else
maxParent->_right = curLeftmax->_right;
delete curLeftmax;
}
return true;
}
}
return false;
}这里实际情况并没有将第一种分化出来,因为当被删除结点的孩子都为空时,其父亲无论指向左孩子还是右孩子仍然同样置空。
其次是最后一种情况只交换两个结点的值,不用再进行复杂的结点迁移,利于直接保持原树顺序。
3.二叉搜索树类代码
cpp
#pragma once
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;
//树结点
template<class K>
struct BSTNode
{
K _key;
BSTNode<K>* _left;
BSTNode<K>* _right;
BSTNode(K x)
:_key(x)
,_left(nullptr)
,_right(nullptr)
{}
};
//二叉搜索树
template<class K>
class BSTree
{
private:
typedef BSTNode<K> Node;
//方便函数内部传参
void _inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_inorder(root->_left);
cout << root->_key << ' ';
_inorder(root->_right);
}
//递归插入
bool _insert(Node*& root, const K& x)
{
if (root == nullptr)
{
root = new Node(x);
return true;
}
if (root->_key == x)
{
return false;
}
return root->_key > x ? _insert(root->_left, x) : _insert(root->_right, x);
}
public:
BSTree() = default;//调用默认构造即可
//插入
bool insert(const K& key)
{
//分为根为空或不为空
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
//不为空则寻找合适位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else if(key == cur->_key)
{
return false; //不插入重复数据
}
}
if (key > parent->_key)
{
parent->_right = new Node(key);
}
else
{
parent->_left = new Node(key);
}
return true;
}
//递归插入
bool REinsert(const K& x)
{
return _insert(_root, x);
}
//删除
bool erase(const K& x)
{
//内部查找
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
parent = cur;
if (cur->_key < x)
{
cur = cur->_right;
}
else if (cur->_key > x)
{
cur = cur->_left;
}
else //找到了,进行分情况删除
{
if(cur->_left == nullptr) //左孩子为空
{
if (cur != _root)
{
//父亲指向不为空的右
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else
{
_root = cur->_right;
}
delete cur;
}
else if(cur->_right == nullptr) //右孩子为空
{
if (cur != _root)
{
//父亲指向不为空的右
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
_root = cur->_left;
}
delete cur;
}
else //左右都不为空
{
//查找合适结点------左子树最大
Node* curLeftmax = cur->_left;
Node* maxParent = cur;
while (curLeftmax->_right)
{
maxParent = curLeftmax;
curLeftmax = curLeftmax->_right;
}
//交换key值
swap(cur->_key, curLeftmax->_key);
if (curLeftmax == maxParent->_left)
maxParent->_left = curLeftmax->_right;
else
maxParent->_right = curLeftmax->_right;
delete curLeftmax;
}
return true;
}
}
return false;
}
//遍历------中序遍历
void inorder()
{
_inorder(_root);
cout << endl;
}
//查找
Node* find(const K& x)
{
assert(_root != nullptr);
Node* cur = _root;
while (cur)
{
if (cur->_key < x)
{
cur = cur->_right;
}
else if (cur->_key > x)
{
cur = cur->_left;
}
else if(cur->_key == x)
{
return cur;
}
}
return nullptr;
}
private:
Node* _root = nullptr;
};