目录

1.摘要
为了提高差分进化算法(DE)在不同优化问题上的性能,本文提出了一种自适应种群分配和变异选择差分进化算法(iDE-APAMS)。iDE-APAMS将变异策略分为探索策略池和开发策略池,不同的变异策略通过合作与竞争动态分配种群资源。策略池之间通过合作竞争种群资源,再由每个策略池内的变异策略相互竞争,从而优化资源分配,变异规模因子和交叉率根据种群多样性和适应度的变化自适应调整。
2.自适应种群分配和变异选择差分进化算法iDE-APAMS
变异策略池
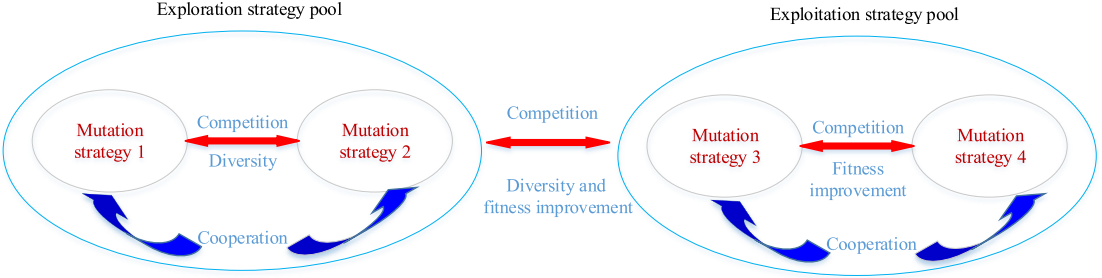
不同的变异策略具有不同的探索性和开发性,影响全局和局部搜索能力。良好的探索性可增强全局搜索,但可能导致发散;而强开发性可加速局部收敛,但易陷入局部最优。论文通过构建探索和开发策略池,动态选择变异策略,平衡探索与开发,优化算法性能。
探索策略池通过引入多样化的变异策略,增强种群多样性和探索能力。变异策略的选择考虑通过差异向量避免相似行为,并将被丢弃的个体存储在外部档案中。
DE/current-to-qbest with archive/1:
ν i , G = x i , G + F i × ( x q b e s t , G − x i , G + x r 1 , G − x r 2 , G ) \nu_{i,G}=x_{i,G}+F_{i}\times(x_{qbest,G}-x_{i,G}+x_{r1,G}-x_{r2,G}) νi,G=xi,G+Fi×(xqbest,G−xi,G+xr1,G−xr2,G)
DE/current-to-rand /1:
ν i , G = x i , G + F i × ( x r 1 , G − x i , G + x r 3 , G − x r 2 , G ) \nu_{i,G}=x_{i,G}+F_i\times(x_{r1,G}-x_{i,G}+x_{r3,G}-x_{r2,G}) νi,G=xi,G+Fi×(xr1,G−xi,G+xr3,G−xr2,G)
开发策略池通过选择具有良好开发性的变异策略,利用精英引导和局部搜索提高个体的开发能力,增强精英周围的搜索能力并提升解的准确性。
DE/current-to-ord_tbest/1:
ν i , G = x i , G + F i × ( x o r d t b e s t , G − x i , G + x o r d t m i d , G − x o r d t b a d , G ) \nu_{i,G}=x_{i,G}+F_i\times(x_{ord_tbest,G}-x_{i,G}+x_{ord_tmid,G}-x_{ord_tbad,G}) νi,G=xi,G+Fi×(xordtbest,G−xi,G+xordtmid,G−xordtbad,G)
CMA-ES:
ν i , G = N ( μ , δ 2 M ) \nu_{i,G}=N(\mu,\delta^2\boldsymbol{M}) νi,G=N(μ,δ2M)
自适应种群分配
自适应种群分配通过基于适应度改善和多样性的动态分配方法,合理分配种群资源。在探索策略池中,优先考虑多样性以提升全局搜索能力;在开发策略池中,优先考虑适应度改善以提高局部搜索精度。
适应度改善:
F i t m = 1 N m ∑ i = 1 N m Δ F i t i , m = 1 , 2 , 3 , 4 Fit^m=\frac{1}{N_m}\sum_{i=1}^{N_m}\Delta Fit_i,m=1,2,3,4 Fitm=Nm1i=1∑NmΔFiti,m=1,2,3,4
Δ F i t i = max ( 0 , f ( x i , G ) − f ( u i , G ) ) \Delta Fit_i=\max(0,f(x_{i,G})-f(u_{i,G})) ΔFiti=max(0,f(xi,G)−f(ui,G))
种群多样性:
D i s m = 1 N m ∑ i = 1 N m Δ D i s i , m = 1 , 2 , 3 , 4 Dis^m=\frac{1}{N_m}\sum_{i=1}^{N_m}\Delta Dis_i,m=1,2,3,4 Dism=Nm1i=1∑NmΔDisi,m=1,2,3,4
Δ D i s i = d i s ( x i , G − x b e s t , G ) \Delta Dis_i=dis(x_{i,G}-x_{best,G}) ΔDisi=dis(xi,G−xbest,G)
探索策略池与开发策略池之间的种群分配基于适应度改善和多样性,同时利用历史记忆存储平滑的适应度改善和多样性。历史记忆的更新:
Z k , G + 1 = min ( 0.8 , max ( 0.2 , Z k , G + 1 ) ) Z_{k,G+1}=\min(0.8,\max(0.2,Z_{k,G+1})) Zk,G+1=min(0.8,max(0.2,Zk,G+1))
Z k , G + 1 = r ⋅ Z k , G + ( 1 − r ) ⋅ Δ c o m R a t e Z_{k,G+1}=r\cdot Z_{k,G}+(1-r)\cdot\Delta comRate Zk,G+1=r⋅Zk,G+(1−r)⋅ΔcomRate
Δ c o m R a t e = ( 1 − η ) ⋅ ∑ m = 1 2 F i t m ∑ m = 1 4 F i t m + η ⋅ ∑ m = 1 2 D i s m ∑ m = 1 4 D i s m \Delta comRate=(1-\eta)\cdot\frac{\sum_{m=1}^2Fit^m}{\sum_{m=1}^4Fit^m}+\eta\cdot\frac{\sum_{m=1}^2Dis^m}{\sum_{m=1}^4Dis^m} ΔcomRate=(1−η)⋅∑m=14Fitm∑m=12Fitm+η⋅∑m=14Dism∑m=12Dism
探索策略池内的种群分配基于种群多样性:
N m = max ( 0.1 , min ( 0.9 , D i s m ∑ m = 1 2 D i s m ) ) ⋅ N p 1 ∀ m = 1 , 2 N_m=\max(0.1,\min(0.9,\frac{Dis^m}{\sum_{m=1}^2Dis^m}))\cdot N_{p1}\quad\forall m=1,2 Nm=max(0.1,min(0.9,∑m=12DismDism))⋅Np1∀m=1,2
开发策略池内的种群分配基于适应度改进:
N m = max ( 0.1 , min ( 0.9 , F i t m ∑ m = 3 4 F i t m ) ) ⋅ N p 2 ∀ m = 3 , 4 N_m=\max(0.1,\min(0.9,\frac{Fit^m}{\sum_{m=3}^4Fit^m}))\cdot N_{p2}\quad\forall m=3,4 Nm=max(0.1,min(0.9,∑m=34FitmFitm))⋅Np2∀m=3,4

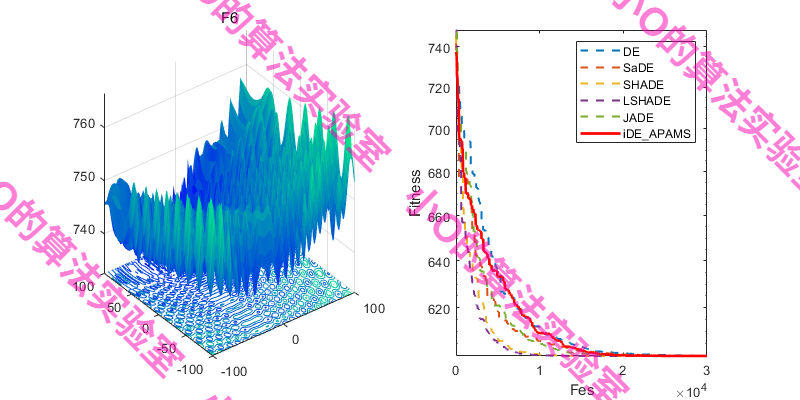
3.结果展示
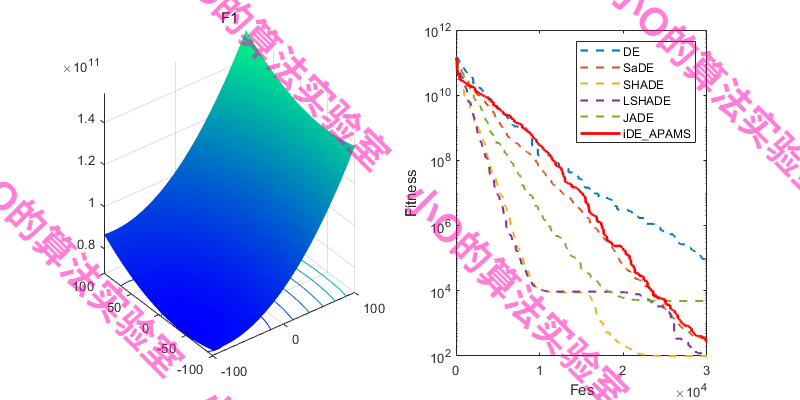
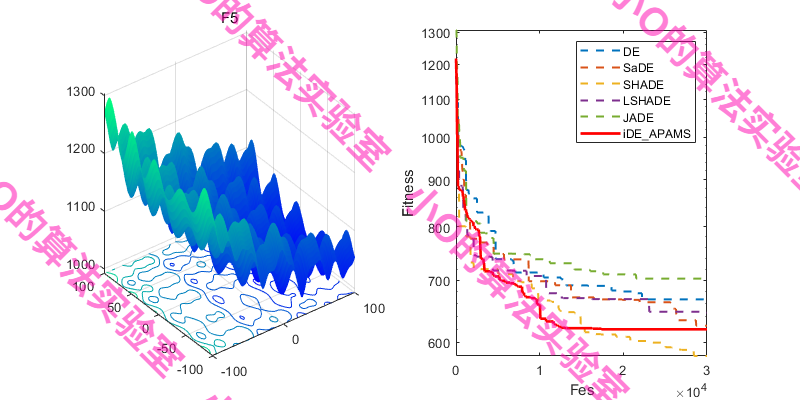
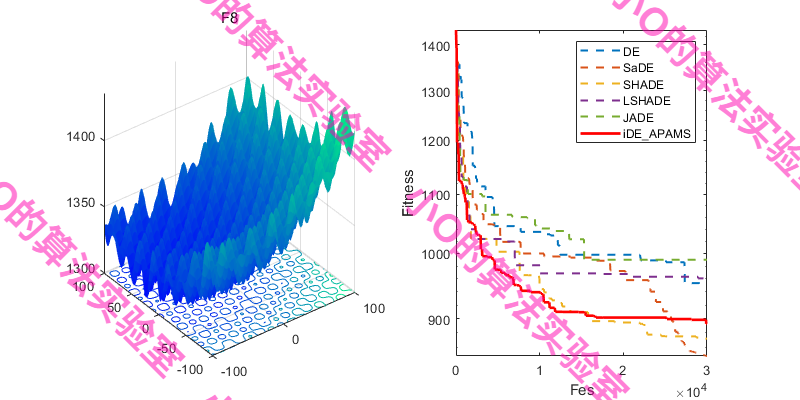
选择CEC冠军算法对比,iDE-APAMS算法效果不错~
4.参考文献
1\] Sun Y, Wu Y, Liu Z. An improved differential evolution with adaptive population allocation and mutation selection\[J\]. Expert Systems With Applications, 2024, 258: 125130. ### 5.代码获取 xx ### 6.算法辅导·应用定制·读者交流 xx