【图像处理】小波变换（Wavelet Transform，WT）

文章目录

一、小波变换的基本原理
二、图像小波变换
- 1、概述
- 2、原理详解
- - [（1）图像小波 - 分解：DWT](#（1）图像小波 - 分解：DWT)
  - [（2）图像小波 - 重构：Inverse DWT](#（2）图像小波 - 重构：Inverse DWT)
- 3、算法流程
- 4、优势
三、函数详解
- [（1）pywt.dwt2()：计算二维离散小波变换（2D DWT）](#（1）pywt.dwt2()：计算二维离散小波变换（2D DWT）)
- [（2）pywt.idwt2()：计算二维离散小波逆变换（2D IDWT）](#（2）pywt.idwt2()：计算二维离散小波逆变换（2D IDWT）)
四、项目实战

在图像领域，小波变换是一种重要的多尺度、多分辨率分析工具，能够有效地提取图像的时频局部信息，广泛应用于图像压缩、去噪、特征提取、纹理分析等多个方面。

一、小波变换的基本原理

1、概述

小波变换（Wavelet Transform，WT）是一种时频分析方法，属于多分辨率分析（Multi-Resolution Analysis, MRA）工具。它通过一组由平移和伸缩操作生成的基函数（小波函数）对信号进行分解，能够同时捕捉局部细节信息（高频）和整体轮廓信息（低频）。

底层原理：小波变换入门（超清晰的思路）

图像处理：小波变换

2、傅里叶变换与小波变换的关系

在信号处理领域，傅里叶变换（Fourier Transform, FT）和小波变换（Wavelet Transform, WT） 都是将信号从时间域映射到频域的重要工具，但侧重点不同。

3、连续小波变换与离散小波变换

对比维度	连续小波变换（CWT）	离散小波变换（DWT）
采样方式	尺度和位移连续采样	尺度和位移离散采样（通常指数/整数序列）
冗余性	高，系数数量多	低，系数少，计算高效
计算复杂度	高	低，适合快速算法
时间-频率分辨率	可在任意时间和频率精细分析	多分辨率分析，分辨率随尺度变化
系数对齐	不严格对齐原信号	对齐原信号（MODWT 除外）
能量守恒	不严格	正交 DWT 保证能量守恒
适用对象	`时间序列信号分析`	`图像和信号均可`
应用场景	瞬态信号检测、精细特征分析、时频可视化（如地震信号、心电图分析）	图像压缩（JPEG2000）、图像去噪、边缘检测、多尺度特征提取（工业检测、医学影像）
优缺点	优点：分析精细，可视化好；缺点：数据量大，计算量高	优点：计算快、适合工业应用；缺点：分辨率固定，局部细节可能不如 CWT 精细

4、按小波基特性分类

基函数的选择影响变换的平滑度、正交性和边缘保留能力。

类型	说明	特点	应用
Haar小波	最简单的阶跃型小波	计算速度快，正交性好，但不平滑	快速压缩、初学演示
Daubechies小波（dbN）	光滑、紧支撑、正交	能量集中，边缘保留效果好	图像压缩、去噪
Symlets（symN）	Daubechies改进，近似对称	对称性更好，减少相位失真	图像去噪、边缘检测
Coiflets	高消失矩，正交小波	能量集中，平滑性强	特征提取、信号分析
Biorthogonal小波	双正交、对称	可分离低频和高频滤波器，边缘保留好	JPEG2000压缩、去噪
Morlet、Mexican Hat等连续小波	主要用于连续小波变换	类似高斯包络正弦波，适合频率分析	时频分析、瞬时频率检测

二、图像小波变换

1、概述

图像小波变换是将二维图像信号进行多尺度、多方向分解的过程。它通过小波函数和尺度函数将图像分为低频（Approximation）和高频（Detail）部分，以便针对不同频率进行分析、处理或压缩。

低频子带（LL）：图像的整体结构信息（轮廓、亮度分布）
高频子带（LH、HL、HH）：图像的细节信息（水平、垂直、对角纹理或边缘）

2、原理详解

（1）图像小波 - 分解：DWT

图像小波变换通常采用二维离散小波变换（2D-DWT）：

（1）行变换

对图像的每一行做一维小波变换，得到低频和高频行信号：

低频行 → 保留行方向的轮廓信息

高频行 → 保留行方向的边缘/细节

（2）列变换

对行变换结果的每一列再做一维小波变换，其将图像分解为四个子带：

LL（低频-低频：图像整体轮廓）

LH（低频-高频：水平边缘）

HL（高频-低频：垂直边缘）

HH（高频-高频：对角纹理与噪声）

这样一层分解完成后，可以进一步对 LL 子带做二级分解，实现多尺度分解。

（3）多尺度分解（Multi-level Decomposition）
每一层 LL 子带可以作为下一层输入继续分解，多层分解能实现逐渐抽象的图像信息提取：

第一层 LL：保留主要轮廓

第二层 LL：更粗略的整体结构

高频子带依旧保留各层的边缘和纹理信息

这种多层分解是图像压缩和去噪的基础。

记忆口诀：低频看轮廓，高频看细节；行列分两次，四宫格呈现。

子带	包含信息	常用处理方式
LL	低频，图像整体轮廓	压缩保留、增强对比度
LH	高频，水平边缘	阈值去噪、边缘增强
HL	高频，垂直边缘	阈值去噪、边缘增强
HH	高频，对角纹理及噪声	去噪、纹理分析

阈值处理（Thresholding）：常用于去噪，保留幅值大的系数，抑制噪声

系数修改：用于图像增强、压缩或特征提取

（2）图像小波 - 重构：Inverse DWT

定义：将处理后的子带通过逆小波变换组合回原图

原理：逆向执行列变换 → 行变换 → 恢复完整图像

特点：

正交小波：能量守恒，重构无失真

双正交小波：重构精确，同时可实现滤波器对称性，减少边缘伪影

3、算法流程

选择小波基（Haar、Daubechies、Symlet 等）

二维分解：对行 → 列做一维小波变换

多尺度迭代分解（可选）

子带处理：压缩、去噪、增强或提取特征

图像重构：逆小波变换恢复处理后图像

4、优势

多分辨率分析：低频-高频分离，边缘和纹理信息明确

局部特征提取：能有效保留局部结构信息

去噪能力强：通过阈值处理高频子带去除噪声

压缩效率高：高频系数可量化或舍弃，实现图像压缩（JPEG2000）

三、函数详解

（1）pywt.dwt2()：计算二维离散小波变换（2D DWT）

python 复制代码

"""#############################################################################################
# 函数功能：计算二维离散小波变换（2D DWT），将二维信号（如图像）分解为低频和高频分量。
# 函数说明：pywt.dwt2(data, wavelet, mode='symmetric', axes=(-2, -1))
# 参数说明：
#         data：输入二维数组（通常是灰度图像或二维信号）。
#         wavelet：小波基名称（如 'haar', 'db1', 'db2', 'coif1' 等）或小波对象。
#         mode：信号边界扩展模式，用于处理边界效应。常见取值：
#             - 'symmetric'（默认）
#             - 'periodization'
#             - 'constant'、'reflect'、'nearest'、'mirror'
#         axes：指定进行小波变换的轴，默认对最后两个轴进行变换（适合二维图像）。
# 返回值：
#         返回一个元组 (cA, (cH, cV, cD))：
#             cA：低频近似系数（Approximation coefficients）。
#             cH：水平方向细节系数（Horizontal detail coefficients）。
#             cV：垂直方向细节系数（Vertical detail coefficients）。
#             cD：对角线方向细节系数（Diagonal detail coefficients）。
# 功能描述：
#         - 将二维信号分解为低频部分和三个高频细节部分，有助于图像压缩、特征提取、去噪等。
# 示例：
import pywt
import numpy as np
import matplotlib.pyplot as plt

# 构造一个简单二维信号（灰度图像）
data = np.array([[1, 2, 3, 4],
                 [5, 6, 7, 8],
                 [9, 10, 11, 12],
                 [13, 14, 15, 16]], dtype=np.float32)

# 进行二维离散小波变换
cA, (cH, cV, cD) = pywt.dwt2(data, wavelet='haar')

# 输出结果
print("低频近似系数 cA:\n", cA)
print("水平细节系数 cH:\n", cH)
print("垂直细节系数 cV:\n", cV)
print("对角线细节系数 cD:\n", cD)
#############################################################################################"""

（2）pywt.idwt2()：计算二维离散小波逆变换（2D IDWT）

python 复制代码

"""#############################################################################################
# 函数功能：计算二维离散小波逆变换（2D Inverse Discrete Wavelet Transform, 2D IDWT），将二维小波分解系数重建为原始二维信号（如图像）。
# 函数说明：pywt.idwt2(coeffs, wavelet, mode='symmetric')
# 参数说明：
#         coeffs：二维小波系数，可以是 (cA, (cH, cV, cD)) 形式，
#                 其中 cA 为低频近似系数，cH、cV、cD 为水平、垂直、对角线细节系数。
#         wavelet：小波基名称（如 'haar', 'db1', 'db2', 'coif1' 等）或小波对象，需与 dwt2 使用的小波一致。
#         mode：信号边界扩展模式，用于处理边界效应。常见取值：
#             - 'symmetric'（默认）
#             - 'periodization'
#             - 'constant'、'reflect'、'nearest'、'mirror'
# 返回值：
#         返回重建后的二维数组，与原始输入二维信号形状相同。
# 功能描述：
#         - 将二维小波分解系数重建回原始信号，用于图像重建、压缩恢复、去噪后重构等。
# 示例：
import pywt
import numpy as np
import matplotlib.pyplot as plt

# 构造一个简单二维信号（灰度图像）
data = np.array([[1, 2, 3, 4],
                 [5, 6, 7, 8],
                 [9, 10, 11, 12],
                 [13, 14, 15, 16]], dtype=np.float32)

# 进行二维离散小波变换
cA, (cH, cV, cD) = pywt.dwt2(data, wavelet='haar')

# 使用逆变换重建原始信号
reconstructed = pywt.idwt2((cA, (cH, cV, cD)), wavelet='haar')

# 输出重建结果
print("重建后的二维信号:\n", reconstructed)
#############################################################################################"""

四、项目实战

python 复制代码

"""pip install opencv-python pywavelets matplotlib"""

import cv2
import pywt
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 1. 读取图像（灰度模式）
img = cv2.imread('../image/image.jpg', cv2.IMREAD_GRAYSCALE)
img = cv2.imread(r"D:\py\BC\brightness_51.2-1.tif", cv2.IMREAD_GRAYSCALE)  # 替换为真实图像路径
if img is None:
    print("图像不存在！")
    exit()

# 2. 执行 2D 离散小波变换（DWT）
coeffs2 = pywt.dwt2(img, 'haar')  # 'haar' 是最简单的小波，可以换成 'db2', 'sym4' 等
LL, (LH, HL, HH) = coeffs2
# LL：低频部分（整体亮度与结构）
# LH：水平高频（垂直边缘）
# HL：垂直高频（水平边缘）
# HH：对角高频（纹理和噪声）

# 3. 显示分解结果
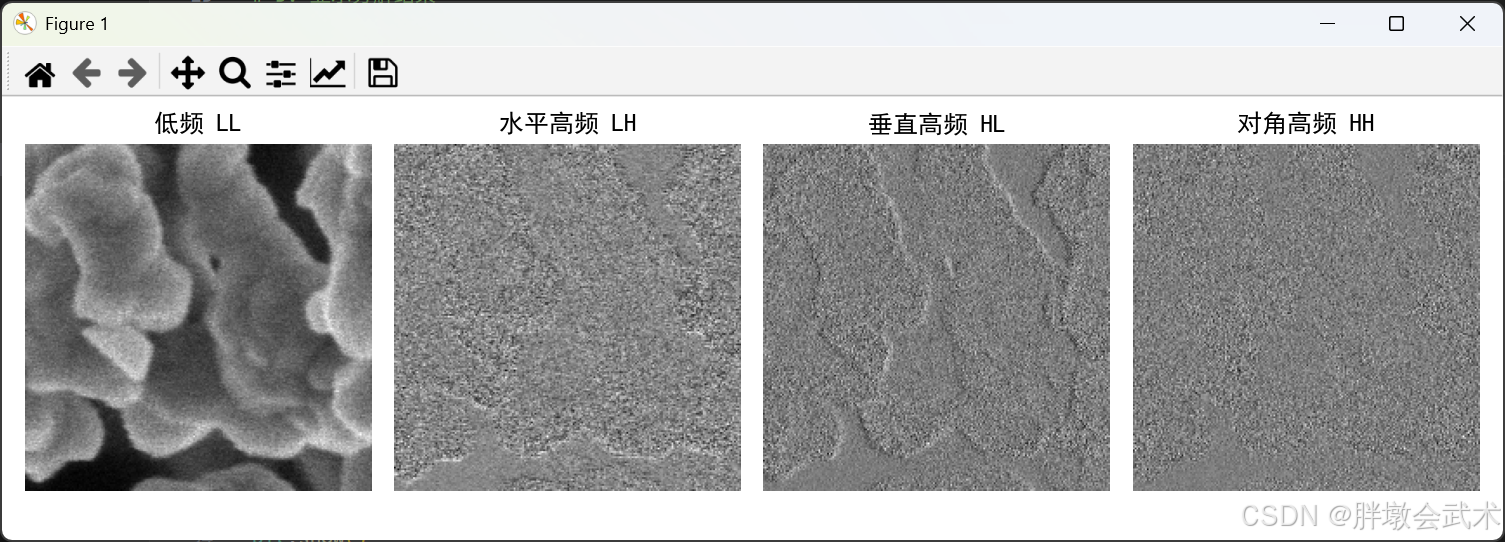
titles = ['低频 LL', '水平高频 LH', '垂直高频 HL', '对角高频 HH']
fig, axes = plt.subplots(1, 4, figsize=(10, 4))
for i, a in enumerate([LL, LH, HL, HH]):
    axes[i].imshow(a, cmap='gray')
    axes[i].set_title(titles[i])
    axes[i].axis('off')

plt.tight_layout()
plt.show()
###################################################################################
# 4. 将分解结果重新组合成图像（重构）
reconstructed_img = pywt.idwt2(coeffs2, 'haar')

# 5. 显示原图与重构图
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1), plt.imshow(img, cmap='gray'), plt.title("原图"), plt.axis('off')
plt.subplot(1, 2, 2), plt.imshow(reconstructed_img, cmap='gray'), plt.title("小波重构图"), plt.axis('off')
plt.tight_layout()
plt.show()