优化AI智能体行为：Q学习、深度Q网络与动态规划在复杂任务中的研究

优化AI智能体行为：Q学习、深度Q网络与动态规划在复杂任务中的研究

引言

在人工智能领域，AI Agent被广泛应用于多种复杂环境中，如自动驾驶、游戏AI、智能机器人等。这些应用的共性在于环境的不确定性和变化性，AI Agent必须具备强大的决策能力，才能在多变的环境中实现最优目标。在这种背景下，动态规划（Dynamic Programming, DP）与优化算法成为解决这一问题的有效工具。本文将探讨如何利用动态规划与优化算法提升AI Agent在复杂环境中的表现，并通过实际代码来展示算法的应用。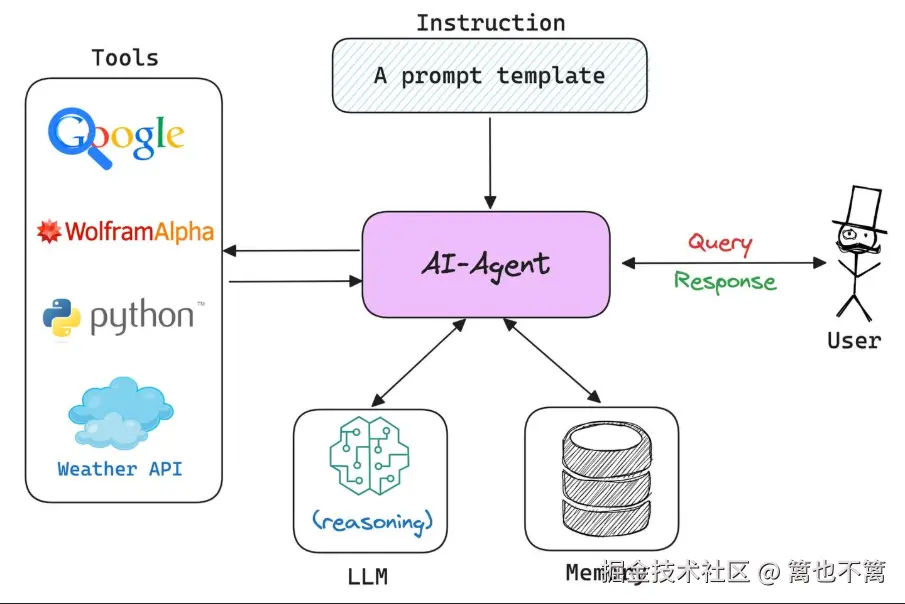

动态规划概述

动态规划是一种分治法思想的扩展，适用于具有最优子结构性质的问题。通过将问题分解成子问题，并存储已解决的子问题结果，动态规划能够有效避免重复计算，减少计算复杂度。动态规划的核心在于找到问题的状态转移方程和边界条件。

动态规划的基本步骤

1. 问题建模：将问题抽象成决策问题，定义状态、决策、奖励等元素。
2. 状态转移方程：根据当前状态和行动来计算下一个状态。
3. 边界条件：定义终止条件，如最终目标状态。
4. 递推求解：根据状态转移方程，通过自底向上的方式求解最优策略。

AI Agent的优化目标

在复杂环境中，AI Agent的主要目标是通过决策过程最大化长期奖励或实现任务目标。优化算法帮助AI Agent在不断变化的环境中调整策略，从而达到最佳性能。以下介绍几种常见的优化算法。

强化学习中的Q学习

Q学习（Q-Learning）是一种无模型的强化学习算法，旨在学习最优的行为策略。通过与环境的交互，AI Agent根据当前状态选择行动，并根据获得的奖励来更新状态-行动值（Q值）。最终，Q值收敛后，AI Agent可以选择最大化Q值的行动。

Q学习的核心公式

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Q ( s t , a t ) = Q ( s t , a t ) + α [ r t + 1 + γ max ⁡ a ′ Q ( s t + 1 , a ′ ) − Q ( s t , a t ) ] Q(s_t, a_t) = Q(s_t, a_t) + \alpha [r_{t+1} + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t)] </math>Q(st,at)=Q(st,at)+α[rt+1+γa′maxQ(st+1,a′)−Q(st,at)]

• <math xmlns="http://www.w3.org/1998/Math/MathML"> s t s_t </math>st：当前状态
• <math xmlns="http://www.w3.org/1998/Math/MathML"> a t a_t </math>at：当前动作
• <math xmlns="http://www.w3.org/1998/Math/MathML"> r t + 1 r_{t+1} </math>rt+1：奖励
• <math xmlns="http://www.w3.org/1998/Math/MathML"> γ \gamma </math>γ：折扣因子
• <math xmlns="http://www.w3.org/1998/Math/MathML"> α \alpha </math>α：学习率

策略梯度方法

策略梯度方法通过直接优化策略函数来提升AI Agent的性能。与Q学习不同，策略梯度方法不依赖于值函数，而是直接学习最优策略的参数。

策略梯度更新公式

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ∇ θ J ( θ ) = E τ ∼ π θ [ ∇ log ⁡ π θ ( a t ∣ s t ) R ( τ ) ] \nabla \theta J(\theta) = \mathbb{E}{\tau \sim \pi\theta} [\nabla \log \pi_\theta(a_t | s_t) R(\tau)] </math>∇θJ(θ)=Eτ∼πθ[∇logπθ(at∣st)R(τ)]

• <math xmlns="http://www.w3.org/1998/Math/MathML"> π θ ( a t ∣ s t ) \pi_\theta(a_t | s_t) </math>πθ(at∣st)：策略函数
• <math xmlns="http://www.w3.org/1998/Math/MathML"> R ( τ ) R(\tau) </math>R(τ)：返回值，即任务的总奖励

动态规划与优化算法结合

AI Agent在面对复杂环境时，通常需要结合动态规划和优化算法，形成更加精确的策略。在一些实际问题中，动态规划用于处理部分环境的状态空间，而优化算法用于处理大规模或高维的环境空间。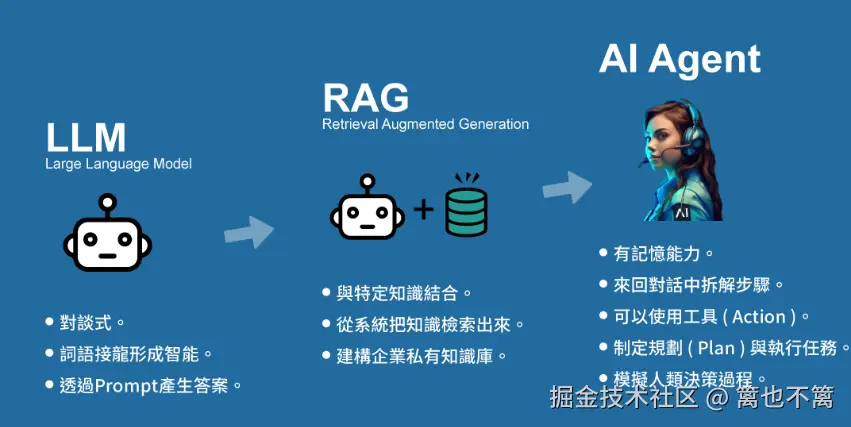

结合Q学习与动态规划

Q学习算法能够在离散的状态空间中使用动态规划思想来更新Q值，使得AI Agent在多步决策中更为高效地学习最优策略。以下是基于Q学习的动态规划示例。

import numpy as np

# 初始化状态空间和Q值表
states = [0, 1, 2, 3]  # 假设有4个状态
actions = [0, 1]  # 假设有2个动作（0: 向左，1: 向右）
Q = np.zeros((len(states), len(actions)))  # 初始化Q表为0

# 奖励函数
reward = np.array([0, 1, -1, 10])  # 每个状态的奖励

# 参数设置
alpha = 0.1  # 学习率
gamma = 0.9  # 折扣因子
epochs = 1000  # 训练轮次

# Q学习算法
for epoch in range(epochs):
    state = np.random.choice(states)  # 随机选择初始状态
    done = False

    while not done:
        action = np.argmax(Q[state]) if np.random.rand() > 0.1 else np.random.choice(actions)  # ε-greedy策略
        next_state = state + (1 if action == 1 else -1)  # 根据动作选择下一个状态
        next_state = max(0, min(next_state, len(states) - 1))  # 保证状态在合法范围内

        # 更新Q值
        Q[state, action] = Q[state, action] + alpha * (reward[next_state] + gamma * np.max(Q[next_state]) - Q[state, action])
        
        state = next_state
        if state == len(states) - 1:
            done = True  # 到达终止状态

print("训练后的Q值表：\n", Q)

结合深度学习的优化策略

在更复杂的环境中，状态空间和动作空间的维度可能非常高，传统的动态规划方法难以直接应用。这时，可以将Q学习与深度学习结合，使用深度Q网络（DQN）来逼近Q值函数，从而应对高维度的问题。

实际应用案例：强化学习的路径规划问题

在实际应用中，AI Agent的动态规划与优化算法可以用于路径规划问题。例如，在自动驾驶系统中，AI Agent需要在复杂的城市交通环境中选择最优路径。

通过强化学习，AI Agent可以根据实时的交通状况、道路信息、行车规则等，实时计算并更新最优路径。在这一过程中，动态规划帮助AI Agent逐步优化路径选择策略，而优化算法则帮助Agent在大规模的环境中快速收敛。

动态规划与优化算法的挑战

尽管动态规划与优化算法能够极大地提升AI Agent的性能，但在应用过程中，仍然存在一些挑战，尤其是在处理高维度、大规模环境时。随着问题规模的增大，状态空间和动作空间的复杂度急剧上升，导致算法的计算量呈指数级增长。这种现象被称为维度灾难 （curse of dimensionality），它使得传统的动态规划方法在实际应用中变得不切实际。

维度灾难与近似算法

为了应对维度灾难，研究者们提出了一些近似算法，如价值迭代 、策略迭代 和模型自由的强化学习方法。这些算法通过减少需要考虑的状态数量或利用函数逼近技术来缩小计算范围，从而使得动态规划能够在复杂环境中得到应用。

价值迭代与策略迭代

• 价值迭代是一种动态规划算法，它通过迭代地更新状态的价值，直到收敛到最优解。每次迭代时，算法会根据当前的状态价值更新每个状态的期望奖励。

• 策略迭代则是通过交替执行策略评估和策略改进来逐步提升决策质量。每次策略评估后，都会通过改进策略来选择当前状态下最优的动作，最终收敛到最优策略。

这两种方法在较低维度的环境中效果较好，但在高维度问题中，仍然可能遇到计算资源耗尽的问题。因此，利用神经网络来近似状态价值函数或策略函数成为了一种可行的解决方案。

深度强化学习的应用

随着深度学习的快速发展，深度强化学习（Deep Reinforcement Learning, DRL）逐渐成为AI Agent解决复杂环境问题的主流方法。深度强化学习通过结合深度神经网络与强化学习，能够有效地处理大规模、高维度的状态和动作空间。深度Q网络（DQN）和近端策略优化（PPO）是目前深度强化学习领域中应用广泛的算法。

深度Q网络（DQN）

DQN将深度神经网络与Q学习结合起来，使用神经网络来逼近Q值函数。这种方法能够处理传统Q学习无法应对的复杂问题。DQN的核心思想是通过神经网络对状态-动作值函数进行逼近，并使用经验回放（experience replay）和固定目标网络（target network）来稳定训练过程。

DQN的训练步骤

1. 初始化神经网络：使用一个深度神经网络来估计Q值函数。
2. 经验回放：将AI Agent与环境交互的经历存储在回放缓冲区中，并从中随机采样以打破数据之间的相关性。
3. 固定目标网络：在训练过程中，目标网络保持不变一段时间，以提高训练的稳定性。
4. Q值更新：根据贝尔曼方程更新Q值。

以下是DQN的简单代码实现：

import numpy as np
import random
import torch
import torch.nn as nn
import torch.optim as optim
from collections import deque

class DQN(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(DQN, self).__init__()
        self.fc1 = nn.Linear(state_dim, 128)
        self.fc2 = nn.Linear(128, 128)
        self.fc3 = nn.Linear(128, action_dim)
    
    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        x = self.fc3(x)
        return x

class ReplayBuffer:
    def __init__(self, capacity=10000):
        self.buffer = deque(maxlen=capacity)
    
    def push(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))
    
    def sample(self, batch_size):
        return random.sample(self.buffer, batch_size)
    
    def size(self):
        return len(self.buffer)

def train_dqn(env, agent, episodes=1000, batch_size=64, gamma=0.99, epsilon=0.1, learning_rate=1e-3):
    optimizer = optim.Adam(agent.parameters(), lr=learning_rate)
    replay_buffer = ReplayBuffer()
    for episode in range(episodes):
        state = env.reset()
        done = False
        total_reward = 0
        while not done:
            # epsilon-greedy strategy
            if random.random() < epsilon:
                action = env.sample_action()
            else:
                state_tensor = torch.tensor(state, dtype=torch.float32)
                action = torch.argmax(agent(state_tensor)).item()

            next_state, reward, done, _ = env.step(action)
            total_reward += reward

            replay_buffer.push(state, action, reward, next_state, done)
            state = next_state

            if replay_buffer.size() >= batch_size:
                batch = replay_buffer.sample(batch_size)
                states, actions, rewards, next_states, dones = zip(*batch)
                
                states_tensor = torch.tensor(states, dtype=torch.float32)
                next_states_tensor = torch.tensor(next_states, dtype=torch.float32)
                actions_tensor = torch.tensor(actions, dtype=torch.long)
                rewards_tensor = torch.tensor(rewards, dtype=torch.float32)
                dones_tensor = torch.tensor(dones, dtype=torch.float32)

                q_values = agent(states_tensor)
                next_q_values = agent(next_states_tensor)
                
                q_value = q_values.gather(1, actions_tensor.unsqueeze(1)).squeeze(1)
                next_q_value = torch.max(next_q_values, dim=1)[0]
                
                target = rewards_tensor + gamma * next_q_value * (1 - dones_tensor)
                
                loss = nn.MSELoss()(q_value, target)
                optimizer.zero_grad()
                loss.backward()
                optimizer.step()

        print(f"Episode {episode+1}/{episodes}, Total Reward: {total_reward}")

# 假设环境的状态空间维度为4，动作空间为2
env = SomeEnvironment()  # 需要定义一个环境类
agent = DQN(state_dim=4, action_dim=2)

train_dqn(env, agent)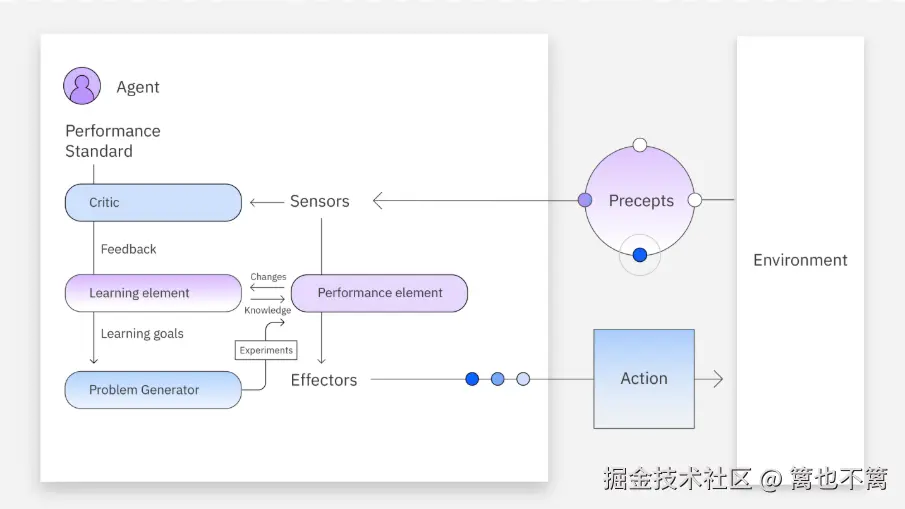

结语

AI Agent在复杂环境中的动态规划与优化算法为智能系统的实现提供了强有力的支持。在面对大规模和高维度问题时，通过引入近似算法和深度学习模型，AI Agent能够在极具挑战的环境中获得高效的决策能力。随着深度强化学习的不断进步，未来的AI Agent将能够处理更加复杂的现实世界问题，进一步推动智能化应用的发展。

AI Agent在复杂环境中的动态规划与优化算法相辅相成，共同推动了智能系统的进步。从Q学习到策略梯度，再到深度Q网络，这些算法在不断进化和优化，帮助AI Agent能够在动态变化的环境中做出最优决策。随着技术的发展，未来的AI Agent将能在更加复杂的环境中实现自适应、高效的决策过程。