Delay Tolerant Networks -- DTNs 延迟容忍网络架构
- 归属
- [Delay Tolerant Networks -- DTNs 延迟容忍网络](#Delay Tolerant Networks – DTNs 延迟容忍网络)
-
- 应用实例
-
- [例子 1:瑞典北部的萨米人 (Saami reindeer herders)](#例子 1:瑞典北部的萨米人 (Saami reindeer herders))
- [例子 2:太平洋中的动物传感网络](#例子 2:太平洋中的动物传感网络)
- DTNs路由方式------存储&转发
- DTNs移动模型
-
- [Random walk 随机游走](#Random walk 随机游走)
-
- [Gauss-Markov Mobility 高斯-马尔可夫移动性](#Gauss-Markov Mobility 高斯-马尔可夫移动性)
- [Random waypoint 随机航点](#Random waypoint 随机航点)
- [Epidemic Routing(流行病路由)------DTNs框架下的路由协议](#Epidemic Routing(流行病路由)——DTNs框架下的路由协议)
- PRoPHET路由协议------DTNs框架下的流行病改进路由协议
归属
延迟容忍网络不属于Data-centric / Hierarchical / Geographical / QoS-based这 4 类里的任何一个。
Data-centric / Hierarchical / Geographical / QoS-based 默认网络端到端连通、可以逐跳转发;而 DTN 的前提恰好相反:长时延、间歇性连接,用 store--carry--forward (存-携-转) 的"机会式/容断"路由范式。所以它通常被单列为 Delay/Disruption-Tolerant(Opportunistic)路由 一大类。
Delay Tolerant Networks -- DTNs 延迟容忍网络
DTN(Delay/Disruption Tolerant Networks,延迟/容断网络)是一类 能够在高时延、大误码率、频繁断连、甚至无持续端到端路径的环境下 仍然提供数据传输服务的网络体系结构。
核心特征:
采用 store--carry--forward(存储--携带--转发) 的路由模式:
当节点之间没有即时可用的链路时,节点会先将消息存储在本地缓存中;
当未来遇到合适的转发机会(例如节点移动到有连接的位置),再将消息转发出去;
通过多次这样的"存--携--转",最终消息能够到达目的地。
应用实例
DTN -- 间歇性连接的 WSN(或自组织网络),其中信息路由延迟是可以容忍的,→存储和转发
例子 1:瑞典北部的萨米人 (Saami reindeer herders)
环境:生活在北极圈附近,地广人稀,通信设施不足。
做法:在 雪地摩托 上装移动中继,牧民移动时携带数据。
应用:牧民的电子邮件、网页缓存等数据通过"存--携--转"的方式带回网络覆盖区,再投递。
👉 说明 DTN 可用于偏远地区人群的基本通信服务。
例子 2:太平洋中的动物传感网络
环境:给 海豹、鲸鱼等动物佩戴温度/位置传感器,帮助测量海洋温度
问题:动物在大洋中移动,节点之间的连接是 间歇性的。
做法:利用动物偶尔相遇时交换/转发数据,最终把数据带到基站(sink)
👉 说明 DTN 可利用"节点移动+偶遇"来完成数据收集。
DTNs路由方式------存储&转发
类似于邮政服务→存储和转发,节点的移动性可以被利用
DTNs移动模型
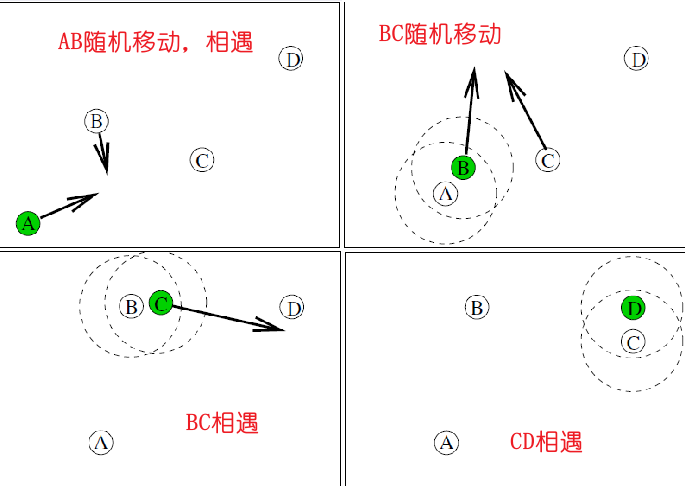
Random walk 随机游走
节点选择移动方向,介于 0 和 2 π 2π 2π 之间,以及给定分布的速度; 例如,均匀、正态分布。
节点以该速度沿该方向(公式如下) 移动指定距离或一段时间。在此期间结束时,节点重复此过程。
Gauss-Markov Mobility 高斯-马尔可夫移动性
节点的速度和方向在第 n n n 时刻由前一时刻、均值以及随机变量共同决定:
s n = α s n − 1 + ( 1 − α ) s ˉ + 1 − α 2 s x n − 1 s_n = \alpha s_{n-1} + (1-\alpha)\bar{s} + \sqrt{1-\alpha^2}\,s_{x_{n-1}} sn=αsn−1+(1−α)sˉ+1−α2 sxn−1
d n = α d n − 1 + ( 1 − α ) d ˉ + 1 − α 2 d x n − 1 d_n = \alpha d_{n-1} + (1-\alpha)\bar{d} + \sqrt{1-\alpha^2}\,d_{x_{n-1}} dn=αdn−1+(1−α)dˉ+1−α2 dxn−1
其中:
- s n s_n sn :第 n n n 时刻的速度
- d n d_n dn :第 n n n 时刻的方向
- s ˉ , d ˉ \bar{s}, \bar{d} sˉ,dˉ :平均速度和平均方向
- s x n − 1 , d x n − 1 s_{x_{n-1}}, d_{x_{n-1}} sxn−1,dxn−1 :来自高斯分布的随机变量 (随机性由此项产生)
- α \alpha α :调节随机性的参数( 0 0 0 = 随机游走, 1 1 1 = 线性运动)
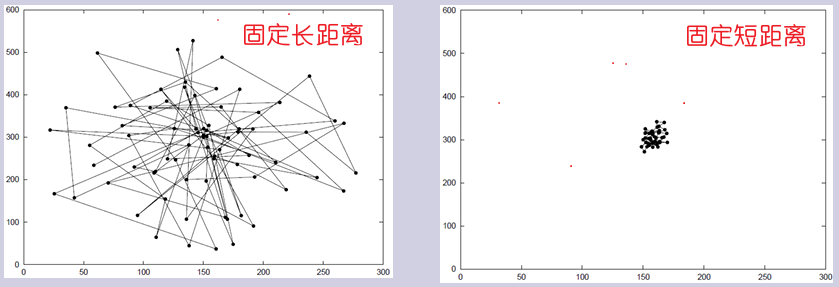
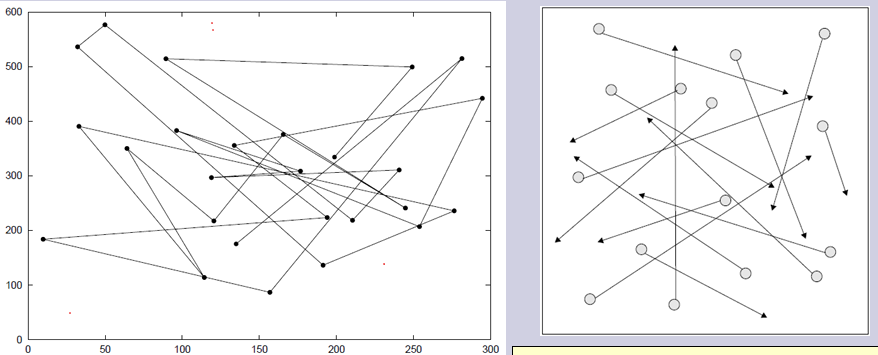
Random waypoint 随机航点
每个节点选择特定区域内的随机点作为其目的地,节点以其选定的速度移动到其目的地。 当节点到达其目的地时,它会停止一段时间,之后它选择一个新的目的地和速度并恢复移动。
第 n n n 时刻节点的位置:
x n = x n − 1 + s n − 1 cos ( d n − 1 ) x_n = x_{n-1} + s_{n-1}\cos(d_{n-1}) xn=xn−1+sn−1cos(dn−1)
y n = y n − 1 + s n − 1 sin ( d n − 1 ) y_n = y_{n-1} + s_{n-1}\sin(d_{n-1}) yn=yn−1+sn−1sin(dn−1)
其中:
- s n − 1 s_{n-1} sn−1 :第 n − 1 n-1 n−1 时刻的速度
- d n − 1 d_{n-1} dn−1 :第 n − 1 n-1 n−1 时刻的方向 [ 0 , 2 π ] [0,2π] [0,2π]
- x , y x,y x,y :坐标位置
Epidemic Routing(流行病路由)------DTNs框架下的路由协议
Based on the theory of epidemic algorithms 基于疫情算法理论
特征:
节点之间相遇时成对交换消息,最终将消息传递到目的地
假设随机移动性模型
核心思想:像病毒传播一样,让消息在节点相遇时被复制并扩散,直到传到目的地。
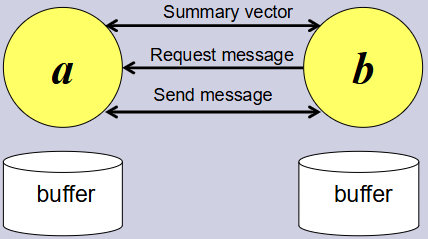
当两个节点相遇时:
交换 summary vector(各自存有哪些消息的索引)。
根据缺失情况请求和发送消息。
节点缓存(buffer)里保存消息。
消息简单结构:全网唯一ID用于识别节点,TTL(生存时间)保证消息不要过度泛滥。

如果缓冲区和 TTL 足够大,则消息会分布在整个网络中,并且传递概率非常高。
如果 TTL = 1,则消息仅传递到目标(如果遇到)
PRoPHET路由协议------DTNs框架下的流行病改进路由协议
PRoPHET (Probabilistic Routing Protocol using History of Encounters and Transitivity)
PRoPHET 是一种 DTN 路由协议 ,改进自 Epidemic Routing。
它利用 节点历史相遇信息 和 转递性 (transitivity),计算消息的投递概率,从而选择性复制消息,减少资源消耗。
核心思想
- 每个节点维护一个投递概率表 P ( a , b ) P(a,b) P(a,b),表示 节点 a a a 把消息送到节点 b b b 的可能性。
- P ( a , b ) ∈ [ 0 , 1 ] P(a,b) \in [0,1] P(a,b)∈[0,1]
- 当两个节点相遇时,交换:
- Summary Vector(消息摘要)
- Delivery Predictability Vector(投递概率信息)
- 只把消息交给 投递概率更高 的节点。
概率更新公式
当节点 a a a 与节点 b b b 相遇时,更新 P ( a , b ) P(a,b) P(a,b):
P ( a , b ) = P ( a , b ) o l d + ( 1 − P ( a , b ) o l d ) × P i n i t P_{(a,b)} = P_{(a,b){old}} + \big(1 - P{(a,b){old}}\big) \times P{init} P(a,b)=P(a,b)old+(1−P(a,b)old)×Pinit
其中:
- P ( a , b ) o l d P_{(a,b)_{old}} P(a,b)old :旧的投递概率
- P i n i t P_{init} Pinit :初始化常数,每次相遇时增加预测值
- 相遇次数越多, P ( a , b ) P(a,b) P(a,b) 越大
📊 与 Epidemic Routing 对比
- Epidemic:见面就复制 → 泛洪式扩散,消耗大
- PRoPHET:基于概率选择性复制 → 更高效
PRoPHET 协议 --- 传递性 (Transitivity)
在 PRoPHET 协议中,如果节点 a 没有直接遇到节点 c ,但是它经常遇到节点 b ,而节点 b 又经常遇到节点 c ,
那么可以认为 a 通过 b 也有一定概率把消息送到 c 。这就是 传递性 (transitivity) 的思想。
概率更新公式
P ( a , c ) = P ( a , c ) o l d + ( 1 − P ( a , c ) o l d ) × P ( a , b ) × P ( b , c ) × β P_{(a,c)} = P_{(a,c){old}} + \Big(1 - P{(a,c){old}}\Big) \times P{(a,b)} \times P_{(b,c)} \times \beta P(a,c)=P(a,c)old+(1−P(a,c)old)×P(a,b)×P(b,c)×β
其中:
- P ( a , c ) o l d P_{(a,c)_{old}} P(a,c)old :a 到 c 的旧投递概率
- P ( a , b ) P_{(a,b)} P(a,b) :a 到 b 的投递概率
- P ( b , c ) P_{(b,c)} P(b,c) :b 到 c 的投递概率
- β \beta β :传递性衰减因子, 0 < β < 1 0 < \beta < 1 0<β<1
b 是 a 的一个良好中继 (relay) :如果 a→b、b→c 的概率都高,那么 a→c 的概率也会增加。
衰减因子 β:避免因为多级传递导致概率无限放大。
总结: PRoPHET 协议利用 直接相遇、老化机制、传递性 三个更新规则,动态调整消息的投递概率,从而比 Epidemic 路由更高效。
PRoPHET 协议(以及 DTN 路由)中的"权衡 (Trade-off)"
多复制 vs 少复制
如果 把消息转发给多个节点(例如 a→b, a→d, a→e),消息最终到达目的地 c 的概率更大。
但问题是:消耗更大(带宽、缓存、能耗)。
👉 这是 高投递率 和 高开销 的权衡。

设置阈值 (Threshold) 转发
选择固定阈值,仅将消息转发到目标具有传递可预测性>阈值的节点 →如果稍后遇到具有更高可预测性的节点怎么办?
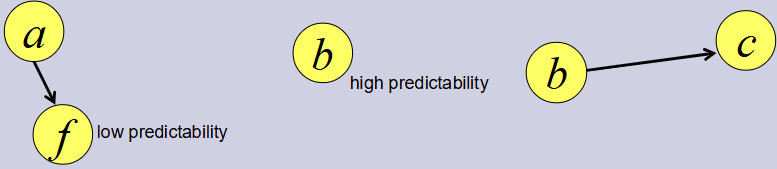
解决方案
规则
当两个节点相遇时,如果对方节点到目标的 投递概率更高,就把消息转发给对方。
如果缓冲区满了,可以用队列管理(比如 FIFO)丢掉旧消息。
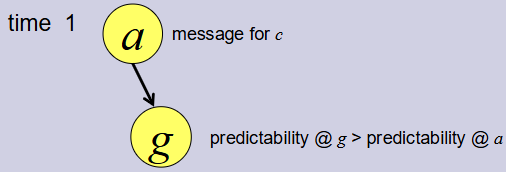
Time 1
节点 a 手里有一个要发给 c 的消息。它遇到了节点 g。
因为 P ( g , c ) > P ( a , c ) P(g,c) > P(a,c) P(g,c)>P(a,c)(g 到 c 的概率比 a 更高),所以 a 把消息转给 g。

Time 2
之后,a 又遇到了节点 e。
P ( e , c ) > P ( a , c ) P(e,c) > P(a,c) P(e,c)>P(a,c),所以 a 再把消息转给 e。
而且 P ( e , c ) > P ( g , c ) P(e,c) > P(g,c) P(e,c)>P(g,c),所以 e 比 g 更适合作为中继。
最终 e 把消息传给 c。
具体实例
A 有一条消息给节点 D
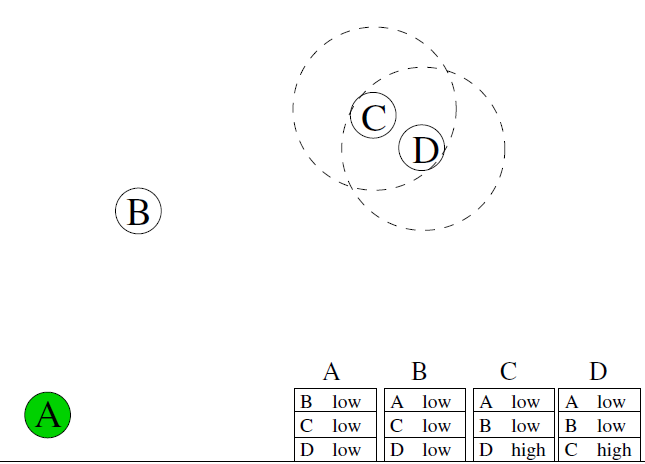
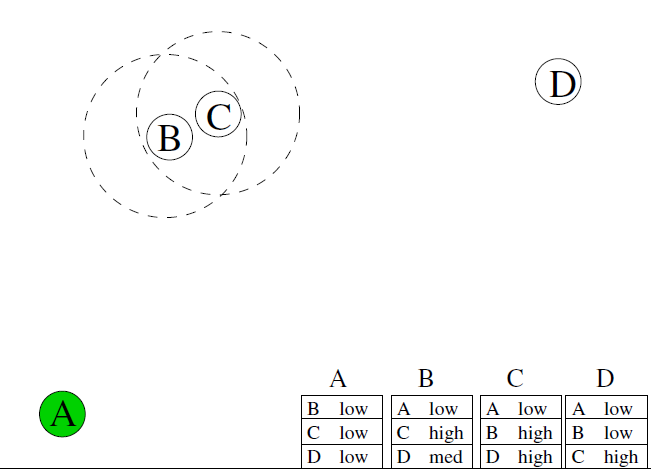
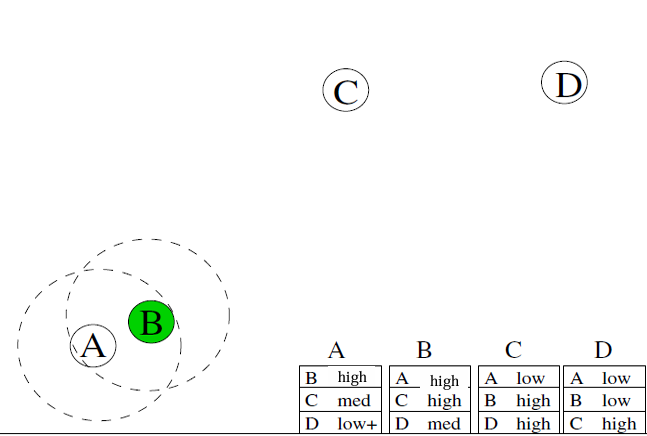
P ( A , D ) < P ( B , D ) P(A,D) < P(B,D) P(A,D)<P(B,D)所以A发给D
P ( B , D ) < P ( C , D ) P(B,D) < P(C,D) P(B,D)<P(C,D)所以B发给C
C 发给D,完成