轻松掌握数据结构：二叉查找树

big_eleven2025-08-19 15:32

二叉搜索树

又叫二叉查找树，BST树

定义

左子树所有节点的值小于根节点，右子树所有节点的值大于根节点（左 < 根 < 右），且左右子树也是这样。

特点

  • 支持高效查找（类似二分查找）（因为当遍历到一个节点的时候，先判断目标值同节点值的大小，然后确定进行左子节点的遍历还是右子节点的遍历，相当于少遍历了一半的数据 ），所以时间复杂度度==O (logn）==

  • 从左到右遍历（中序遍历）可得到一个有序的序列。

  • ==BST通常不允许重复的值==

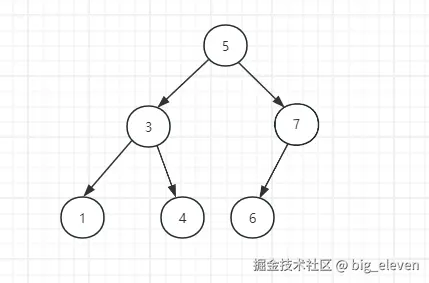
缺点：

当依次插入的数据都比上一个数据值大时，所有的节点就会依次堆到右子节点，此时树就成了一个链表的结构了，查询时间复杂度就降为了==O(n)==

代码实现：

java 复制代码 
package com.stu.shujujiegou;

/**
 * @title:
 * @auther: eleven
 * @description:
 * @data: 2025/8/5 16:45
 * @parm:
 * @return:
 */
import java.util.ArrayList;
import java.util.List;

public class BinarySearchTree {
    // 二叉搜索树节点类
    private static class TreeNode {
        int val;
        TreeNode left;  // 左子节点
        TreeNode right; // 右子节点

        public TreeNode(int val) {
            this.val = val;
            this.left = null;
            this.right = null;
        }
    }

    private TreeNode root; // 根节点

    // 构造空树
    public BinarySearchTree() {
        root = null;
    }

    /**
     * 插入元素
     * @param val 要插入的值
     */
    public void insert(int val) {
        root = insertRecursive(root, val);
    }

    // 递归插入
    private TreeNode insertRecursive(TreeNode current, int val) {
        // 如果当前节点为空，创建新节点作为插入位置
        if (current == null) {
            return new TreeNode(val);
        }

        // 根据值的大小决定插入左子树还是右子树
        if (val < current.val) {
            current.left = insertRecursive(current.left, val);
        } else if (val > current.val) {
            current.right = insertRecursive(current.right, val);
        }
        // 相等的值不插入（BST通常不允许重复值）

        return current;
    }

    /**
     * 查找元素
     * @param val 要查找的值
     * @return 找到返回true，否则返回false
     */
    public boolean contains(int val) {
        return containsRecursive(root, val);
    }

    // 递归查找
    private boolean containsRecursive(TreeNode current, int val) {
        // 节点为空，未找到
        if (current == null) {
            return false;
        }

        // 找到匹配的值
        if (val == current.val) {
            return true;
        }

        // 小于当前节点值，去左子树查找；否则去右子树查找
        return val < current.val
                ? containsRecursive(current.left, val)
                : containsRecursive(current.right, val);
    }

    /**
     * 删除元素
     * @param val 要删除的值
     * @return 删除成功返回true，否则返回false
     */
    public boolean delete(int val) {
        // 如果树为空，直接返回false
        if (root == null) {
            return false;
        }

        // 记录删除前是否包含该值
        boolean exists = contains(val);
        if (exists) {
            root = deleteRecursive(root, val);
        }
        return exists;
    }

    // 递归删除
    private TreeNode deleteRecursive(TreeNode current, int val) {
        if (current == null) {
            return null;
        }

        // 1. 查找要删除的节点
        if (val < current.val) {
            current.left = deleteRecursive(current.left, val);
        } else if (val > current.val) {
            current.right = deleteRecursive(current.right, val);
        } else {
            // 2. 找到要删除的节点，处理三种情况

            // 情况1：叶子节点（没有子节点）
            if (current.left == null && current.right == null) {
                return null;
            }

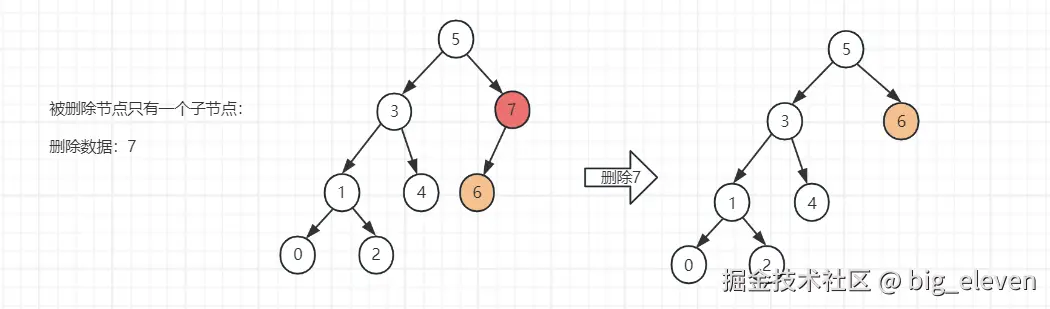
            // 情况2：只有一个子节点
            if (current.left == null) {
                return current.right; // 返回右子节点
            }
            if (current.right == null) {
                return current.left;  // 返回左子节点
            }

            // 情况3：有两个子节点
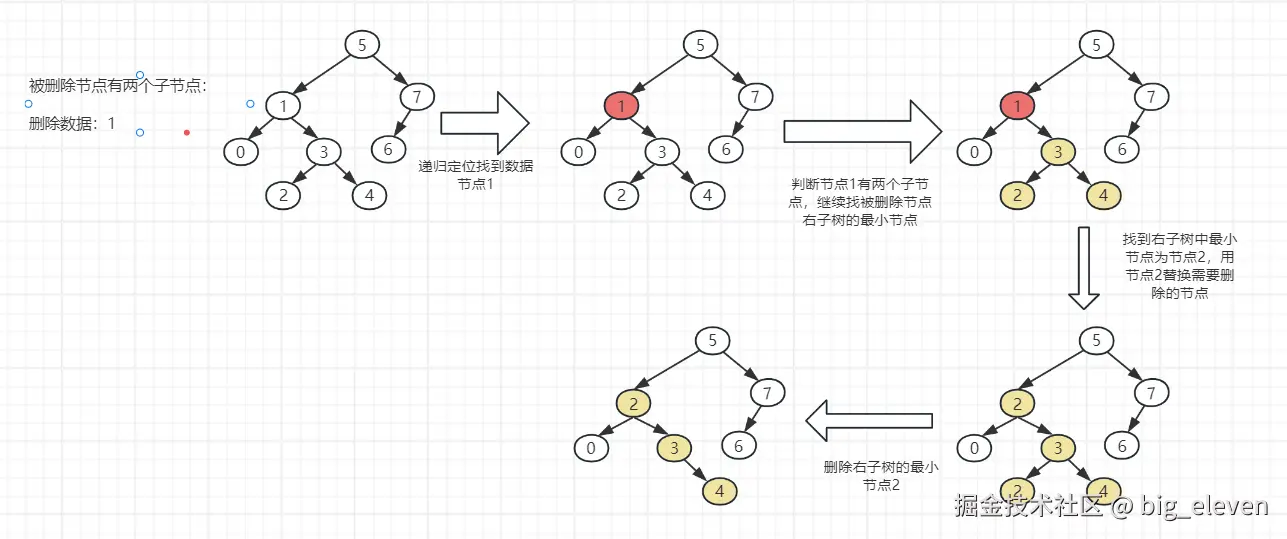
            // 因为二叉搜索树 数据有序满足 左<中<右，所以我们删除当前节点后，需要找到右子树的最小节点替换到当前位置
            // 找到右子树中的最小值节点
            TreeNode smallestNode = findSmallest(current.right);
            // 用最小值替换当前节点值
            current.val = smallestNode.val;
            // 删除右子树中的最小值节点
            current.right = deleteRecursive(current.right, smallestNode.val);
        }

        return current;
    }

    // 查找最小节点（最左节点）
    private TreeNode findSmallest(TreeNode node) {
        return node.left == null ? node : findSmallest(node.left);
    }

    // 查找最大节点（最右节点）
    private TreeNode findLargest(TreeNode node) {
        return node.right == null ? node : findLargest(node.right);
    }

    /**
     * 获取最小值
     * @return 树中的最小值
     */
    public int findMin() {
        if (root == null) {
            throw new IllegalStateException("树为空，无法查找最小值");
        }
        return findSmallest(root).val;
    }

    /**
     * 获取最大值
     * @return 树中的最大值
     */
    public int findMax() {
        if (root == null) {
            throw new IllegalStateException("树为空，无法查找最大值");
        }
        return findLargest(root).val;
    }

    /**
     * 前序遍历（根 -> 左 -> 右）
     * @return 遍历结果列表
     */
    public List<Integer> preOrder() {
        List<Integer> result = new ArrayList<>();
        preOrderRecursive(root, result);
        return result;
    }

    private void preOrderRecursive(TreeNode node, List<Integer> result) {
        if (node != null) {
            result.add(node.val);          // 访问根节点
            preOrderRecursive(node.left, result);  // 遍历左子树
            preOrderRecursive(node.right, result); // 遍历右子树
        }
    }

    /**
     * 中序遍历（左 -> 根 -> 右）
     * 对于BST，中序遍历结果是升序的
     * @return 遍历结果列表
     */
    public List<Integer> inOrder() {
        List<Integer> result = new ArrayList<>();
        inOrderRecursive(root, result);
        return result;
    }

    private void inOrderRecursive(TreeNode node, List<Integer> result) {
        if (node != null) {
            inOrderRecursive(node.left, result);   // 遍历左子树
            result.add(node.val);          // 访问根节点
            inOrderRecursive(node.right, result);  // 遍历右子树
        }
    }

    /**
     * 后序遍历（左 -> 右 -> 根）
     * @return 遍历结果列表
     */
    public List<Integer> postOrder() {
        List<Integer> result = new ArrayList<>();
        postOrderRecursive(root, result);
        return result;
    }

    private void postOrderRecursive(TreeNode node, List<Integer> result) {
        if (node != null) {
            postOrderRecursive(node.left, result);  // 遍历左子树
            postOrderRecursive(node.right, result); // 遍历右子树
            result.add(node.val);          // 访问根节点
        }
    }

    /**
     * 层序遍历（按层次从上到下，从左到右）
     * @return 遍历结果列表
     */
    public List<Integer> levelOrder() {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }

        // 使用队列实现层序遍历
        java.util.Queue<TreeNode> queue = new java.util.LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            result.add(node.val);

            // 左子节点入队
            if (node.left != null) {
                queue.add(node.left);
            }
            // 右子节点入队
            if (node.right != null) {
                queue.add(node.right);
            }
        }
        return result;
    }

    /**
     * 清空树
     */
    public void clear() {
        root = null;
    }

    /**
     * 检查树是否为空
     * @return 空返回true，否则返回false
     */
    public boolean isEmpty() {
        return root == null;
    }

    // 测试方法
    public static void main(String[] args) {
        BinarySearchTree bst = new BinarySearchTree();

        // 插入元素
        bst.insert(50);
        bst.insert(30);
        bst.insert(70);
        bst.insert(20);
        bst.insert(40);
        bst.insert(60);
        bst.insert(80);

        System.out.println("中序遍历（升序）: " + bst.inOrder());
        // 输出: [20, 30, 40, 50, 60, 70, 80]

        System.out.println("前序遍历: " + bst.preOrder());
        // 输出: [50, 30, 20, 40, 70, 60, 80]

        System.out.println("后序遍历: " + bst.postOrder());
        // 输出: [20, 40, 30, 60, 80, 70, 50]

        System.out.println("层序遍历: " + bst.levelOrder());
        // 输出: [50, 30, 70, 20, 40, 60, 80]

        System.out.println("最小值: " + bst.findMin());  // 输出: 20
        System.out.println("最大值: " + bst.findMax());  // 输出: 80
        System.out.println("是否包含60: " + bst.contains(60));  // 输出: true
        System.out.println("是否包含90: " + bst.contains(90));  // 输出: false

        // 删除元素
        bst.delete(30);
        System.out.println("删除30后的中序遍历: " + bst.inOrder());
        // 输出: [20, 40, 50, 60, 70, 80]

        bst.delete(50);
        System.out.println("删除50后的中序遍历: " + bst.inOrder());
        // 输出: [20, 40, 60, 70, 80]
    }
}

重点看数据插入和数据删除

数据插入：

java 复制代码 
/**
 * 插入元素
 * @param val 要插入的值
 */
public void insert(int val) {
    root = insertRecursive(root, val);
}

// 递归插入
private TreeNode insertRecursive(TreeNode current, int val) {
    // 如果当前节点为空，创建新节点作为插入位置
    if (current == null) {
        return new TreeNode(val);
    }

    // 根据值的大小决定插入到左子树还是右子树
    if (val < current.val) {
        current.left = insertRecursive(current.left, val);
    } else if (val > current.val) {
        current.right = insertRecursive(current.right, val);
    }
    // 相等的值不插入（BST通常不允许重复值）
    return current;
}

数据删除：

java 复制代码 
/**
 * 删除元素
 * @param val 要删除的值
 * @return 删除成功返回true，否则返回false
 */
public boolean delete(int val) {
    // 如果树为空，直接返回false
    if (root == null) {
        return false;
    }

    // 记录删除前是否包含该值
    boolean exists = contains(val);
    if (exists) {
        root = deleteRecursive(root, val);
    }
    return exists;
}

// 递归删除
private TreeNode deleteRecursive(TreeNode current, int val) {
    if (current == null) {
        return null;
    }

    // 1. 查找要删除的节点
    if (val < current.val) {
        current.left = deleteRecursive(current.left, val);
    } else if (val > current.val) {
        current.right = deleteRecursive(current.right, val);
    } else {
        // 2. 找到要删除的节点，处理三种情况
        // 情况1：叶子节点（没有子节点）
        if (current.left == null && current.right == null) {
            return null;
        }

        // 情况2：只有一个子节点
        if (current.left == null) {
            return current.right; // 返回右子节点
        }
        if (current.right == null) {
            return current.left;  // 返回左子节点
        }

        // 情况3：有两个子节点
        // 因为二叉搜索树 数据有序且满足 左<中<右，所以我们删除当前节点后，需要找到右子树的最小节点替换到当前位置
        // 找到右子树中的最小值节点
        TreeNode smallestNode = findSmallest(current.right);
        // 用最小值替换当前节点值
        current.val = smallestNode.val;
        // 删除右子树中的最小值节点
        current.right = deleteRecursive(current.right, smallestNode.val);
    }

    return current;
}

对应代码中==情况2==，只有一个子节点：

对应代码中==情况3==：被删除节点有两个子节点：

相关推荐
智驱力人工智能1 天前
守护生命的水上之眼 无人机人员落水检测系统的技术攻坚与应用实践 无人机溺水识别 山区水库无人机落水检测系统 水域安全无人机部署指南
大数据·人工智能·算法·安全·无人机·边缘计算
hweiyu001 天前
排序算法选型决策树
算法·排序算法
JaguarJack1 天前
PHP 之高级面向对象编程 深入理解设计模式、原则与性能优化
后端·php
蓝色汪洋1 天前
xtu oj矩阵
算法
章豪Mrrey nical1 天前
前后端分离工作详解Detailed Explanation of Frontend-Backend Separation Work
后端·前端框架·状态模式
hh随便起个名1 天前
力扣二叉树的三种遍历
javascript·数据结构·算法·leetcode
写写闲篇儿1 天前
微软面试之白板做题
面试·职场和发展
派大鑫wink1 天前
【JAVA学习日志】SpringBoot 参数配置：从基础到实战，解锁灵活配置新姿势
java·spring boot·后端
程序员爱钓鱼1 天前
Node.js 编程实战：文件读写操作
前端·后端·node.js
xUxIAOrUIII1 天前
【Spring Boot】控制器Controller方法
java·spring boot·后端
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04BongoCat - 跨平台键盘猫动画工具05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07sqli-labs靶场通关笔记：第18-19关 HTTP头部注入08jdk21下载、安装（Windows、Linux、macOS）09RedissonClient的配置解析10Open-AutoGLM Windows 安装部署教程