二叉堆介绍
二叉堆(Binary Heap)是一种特殊的完全二叉树,用于实现优先队列、堆排序(Heapsort)等。它有两种类型:最小堆(Min Heap)和最大堆(Max Heap)。在最小堆中,父节点的值总是小于或等于其子节点的值;而在最大堆中,父节点的值总是大于或等于其子节点的值。这确保了堆顶元素(即根节点)分别是整个堆中的最小值(对于最小堆)或最大值(对于最大堆),从而可以高效地获取最小或最大元素。 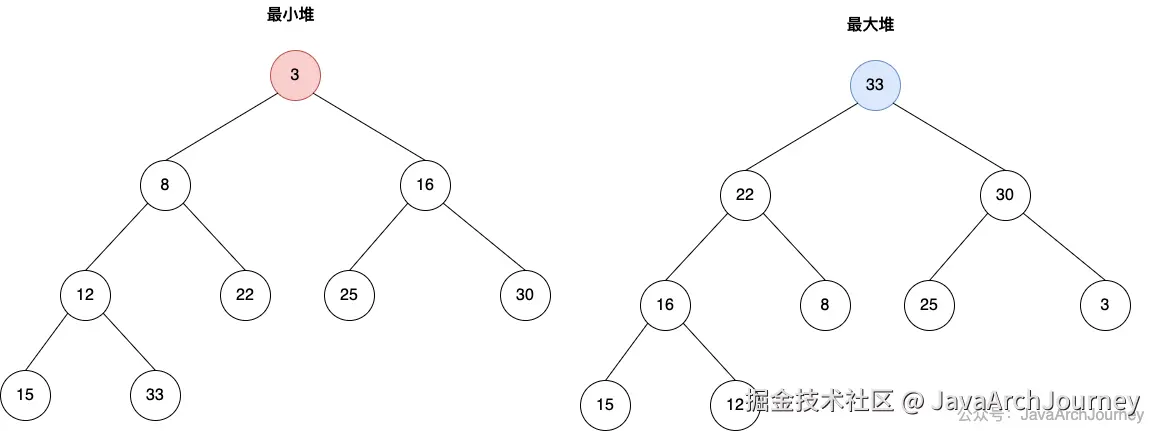
PriorityQueue介绍
PriorityQueue 是一个基于二叉堆实现的无界优先队列。它实现了 Queue 接口,并且不允许插入 null 元素。优先队列中的元素根据它们的自然顺序或者由构造函数提供的 Comparator 来进行排序。
PriorityQueue 在需要对元素进行优先级排序时非常有用,比如任务调度系统中,可以根据任务的紧急程度来处理它们。
PriorityQueue特点如下:
- 优先级排序 :元素按照自然顺序或自定义比较器(
Comparator)来排序。 - 无界队列:理论上可以无限增长,实际上受限于可用内存。
- 非线程安全 :不保证多线程环境下的同步访问,如果需要线程安全的实现,可以考虑
PriorityBlockingQueue。
PriorityQueue使用示例
基本操作示例
创建一个整数类型的优先队列,并进行一些基本操作:
java
import java.util.PriorityQueue;
public class PriorityQueueExample {
public static void main(String[] args) {
// 创建一个整数类型的优先队列,默认是最小堆
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
// 添加元素到队列
priorityQueue.offer(10);
priorityQueue.offer(20);
priorityQueue.offer(5);
System.out.println("队列头部元素(最小元素):" + priorityQueue.peek());
// 移除并返回队列头部元素
Integer headElement = priorityQueue.poll();
System.out.println("已移除的队列头部元素:" + headElement);
// 再次打印队列头部元素
System.out.println("新的队列头部元素:" + priorityQueue.peek());
// 打印剩余的所有元素
System.out.println("队列剩余的所有元素:");
while (!priorityQueue.isEmpty()) {
System.out.println(priorityQueue.poll());
}
}
}运行结果:
java
队列头部元素(最小元素):5
已移除的队列头部元素:5
新的队列头部元素:10
队列剩余的所有元素:
10
20自定义对象比较示例
如果想对自定义对象使用 PriorityQueue,需要确保该对象实现了 Comparable 接口,或者在创建 PriorityQueue 时提供一个 Comparator 来定义排序规则。
例如,现在有一个 Person 类,希望根据年龄来排序:
java
import java.util.Comparator;
import java.util.PriorityQueue;
class Person {
String name;
int age;
Person(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "Person{name='" + name + "', age=" + age + '}';
}
}
public class CustomPriorityQueueExample {
public static void main(String[] args) {
PriorityQueue<Person> pq = new PriorityQueue<>(new Comparator<Person>() {
@Override
public int compare(Person p1, Person p2) {
// 按照年龄升序排序
return Integer.compare(p1.age, p2.age);
}
});
pq.offer(new Person("Alice", 30));
pq.offer(new Person("Bob", 25));
pq.offer(new Person("Charlie", 35));
System.out.println("按年龄排序后的人员列表:");
while (!pq.isEmpty()) {
System.out.println(pq.poll());
}
}
}运行结果:
java
按年龄排序后的人员列表:
Person{name='Bob', age=25}
Person{name='Alice', age=30}
Person{name='Charlie', age=35}PriorityQueue源码分析
以 JDK 1.8 为例,对 PriorityQueue 源码实现进行分析如下:
存储结构
PriorityQueue 使用的是二叉堆(默认是最小堆),通过完全二叉树实现。实际上,二叉堆使用数组来存储堆中的元素(Object[] queue),对于索引为 i 的节点,其左子节点位于 2*i + 1,右子节点位于 2*i + 2,而父节点位于 (i-1)/2(取整数部分)。
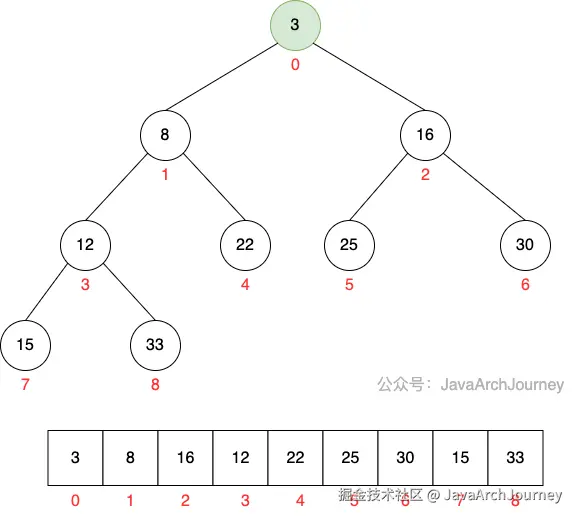
java
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
private static final long serialVersionUID = -7720805057305804111L;
/**
* 默认的初始容量
*/
private static final int DEFAULT_INITIAL_CAPACITY = 11;
/**
* 完全二叉树实现最小堆(min-heap)。使用数组存放优先队列中的元素
* non-private 是为了让嵌套类(比如迭代器)访问更方便
*/
transient Object[] queue; // non-private to simplify nested class access
/**
* 队列中实际元素的数量
*/
private int size = 0;
/**
* 队列中的元素进行排序的比较器对象
* 如果构造 PriorityQueue 时没有传入比较器,则使用元素的自然顺序(要求元素实现 Comparable 接口)
*/
private final Comparator<? super E> comparator;
}构造方法
PriorityQueue 提供了多个构造方法,允许指定初始容量(默认为 11 )、比较器( Comparator )以及从其他集合(Collection、PriorityQueue 或者 SortedSet)初始化队列。
java
/**
* 无参构造函数:默认容量(11) + 自然排序(comparator = null)
*/
public PriorityQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
/**
* 指定容量 + 自然排序(comparator = null)
*/
public PriorityQueue(int initialCapacity) {
this(initialCapacity, null);
}
/**
* 默认容量(11) + 自定义比较器
*/
public PriorityQueue(Comparator<? super E> comparator) {
this(DEFAULT_INITIAL_CAPACITY, comparator);
}
/**
* 自定义容量和比较器
*/
public PriorityQueue(int initialCapacity,
Comparator<? super E> comparator) {
// 如果初始容量小于 1,抛出异常。为了兼容 Java 1.5
// Note: This restriction of at least one is not actually needed,
// but continues for 1.5 compatibility
if (initialCapacity < 1)
throw new IllegalArgumentException();
// 初始化堆数组
this.queue = new Object[initialCapacity];
// 保存比较器
this.comparator = comparator;
}
/**
* 从任意集合初始化
*/
@SuppressWarnings("unchecked")
public PriorityQueue(Collection<? extends E> c) {
// 根据传入集合的类型选择不同的初始化逻辑
if (c instanceof SortedSet<?>) {
// 若是 SortedSet 类型:使用 SortedSet 的比较器
SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
this.comparator = (Comparator<? super E>) ss.comparator();
// 初始化堆(可以不重新调整堆结构,因为 SortedSet 中元素已是有序)
initElementsFromCollection(ss);
}
else if (c instanceof PriorityQueue<?>) {
// 若是 PriorityQueue 类型:复制原队列的比较器
PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
this.comparator = (Comparator<? super E>) pq.comparator();
// 初始化堆,并重新调整堆结构
initFromPriorityQueue(pq);
}
else {
// 其他类型(如 List、Set)
// 使用自然排序(要求元素实现 Comparable)
this.comparator = null;
// 初始化堆,并重新调整堆结构
initFromCollection(c);
}
}
private void initFromPriorityQueue(PriorityQueue<? extends E> c) {
// 检查传入的 PriorityQueue 是否是标准的 PriorityQueue 实例
if (c.getClass() == PriorityQueue.class) {
// 如果是,则直接使用 toArray() 和 size() 方法获取元素数组和大小,避免额外的转换开销
this.queue = c.toArray();
this.size = c.size();
} else {
// 如果不是标准的 PriorityQueue 实例(例如可能是自定义子类),则通过 initFromCollection() 方法进行更通用的初始化处理
initFromCollection(c);
}
}
private void initFromCollection(Collection<? extends E> c) {
// 将集合中的元素复制到当前队列的 queue 数组中,并设置大小
initElementsFromCollection(c);
// 重新调整堆结构
heapify();
}
private void initElementsFromCollection(Collection<? extends E> c) {
// 将集合转换为对象数组
Object[] a = c.toArray();
// If c.toArray incorrectly doesn't return Object[], copy it.
// 检查是否返回的是 Object[] 类型的数组
if (a.getClass() != Object[].class)
// 如果不是,则使用 Arrays.copyOf() 方法创建一个新的 Object[] 数组并拷贝元素
a = Arrays.copyOf(a, a.length, Object[].class);
// 如果集合长度为 1 或者存在比较器(即需要自定义排序),遍历数组检查是否存在 null 元素
int len = a.length;
if (len == 1 || this.comparator != null)
for (int i = 0; i < len; i++)
if (a[i] == null)
// PriorityQueue 不允许存储 null 元素,因此发现 null 时抛出异常
throw new NullPointerException();
// 赋值与设置大小
this.queue = a;
this.size = a.length;
}建堆过程
建堆方法 heapify() 用于把一个数组的元素从无序构建成最小堆排序。
java
/**
* 建堆方法,确保整个数组满足最小堆的性质,即每个节点都小于或等于其子节点
*/
@SuppressWarnings("unchecked")
private void heapify() {
// 循环从最后一个非叶子节点开始((size >>> 1) - 1),一直到根节点(索引为0)
// (size >>> 1) - 1:使用无符号右移操作符来计算最后一个非叶子节点的索引。因为完全二叉树中,所有大于 size/2 - 1 的索引都是叶子节点
// heapify 过程只需要从最后一个非叶子节点开始向上处理到根节点(索引为0)即可,因为叶子节点本身已经满足最小堆的性质(它们没有子节点)
for (int i = (size >>> 1) - 1; i >= 0; i--)
// 对每个节点调用 siftDown() 方法,将该节点向下调整到合适的位置,以保持堆的性质
siftDown(i, (E) queue[i]);
}
private void siftDown(int k, E x) {
// 根据是否存在比较器选择不同的下滤方式
if (comparator != null)
// 使用自定义比较器 Comparator
siftDownUsingComparator(k, x);
else
// 使用元素的自然顺序(通过 Comparable 接口)进行比较
siftDownComparable(k, x);
}
@SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
// 备注:基于完全二叉树的性质,在数组表示中,所有大于 size / 2 - 1 的索引都是叶子节点(这些节点没有子节点)
// half 标识二叉堆最后一个非叶子节点的位置
int half = size >>> 1;
// 只要当前节点不是叶子节点(k < half),就继续循环
while (k < half) {
// 找到当前节点的左右子节点中的较小者
int child = (k << 1) + 1; // (k << 1) + 1:计算左子节点索引
Object c = queue[child];
int right = child + 1;
if (right < size &&
comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right];
// 如果当前节点比这个较小者更小/相等,说明当前子堆已是最小堆,不用继续向下调整,跳出循环
if (comparator.compare(x, (E) c) <= 0)
break;
// 如果当前节点比这个较小者大,则交换两个元素,并更新当前节点索引 k 继续下一轮比较(继续向下调整)
queue[k] = c;
k = child;
}
// 将 x 放在正确的位置上
queue[k] = x;
}
@SuppressWarnings("unchecked")
private void siftDownComparable(int k, E x) {
// 当没有提供比较器时,使用元素自身的 Comparable 接口来进行比较和调整
// 循环逻辑与 siftDownUsingComparator() 基本相同,只是比较的方式不同,使用的是 compareTo() 方法而不是 compare()
Comparable<? super E> key = (Comparable<? super E>)x;
int half = size >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = queue[child];
int right = child + 1;
if (right < size &&
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
c = queue[child = right];
if (key.compareTo((E) c) <= 0)
break;
queue[k] = c;
k = child;
}
queue[k] = key;
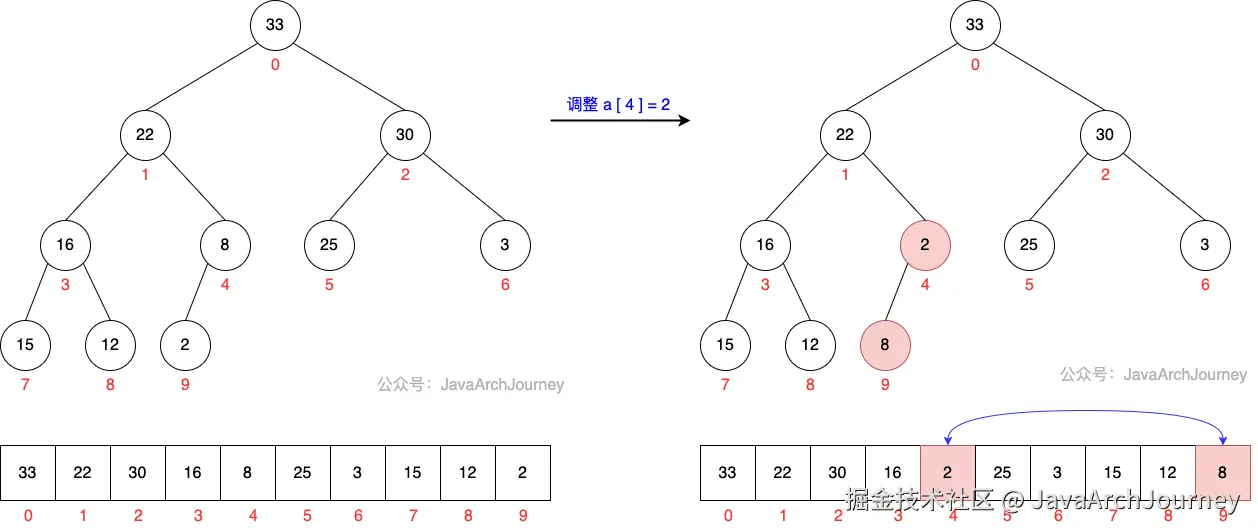
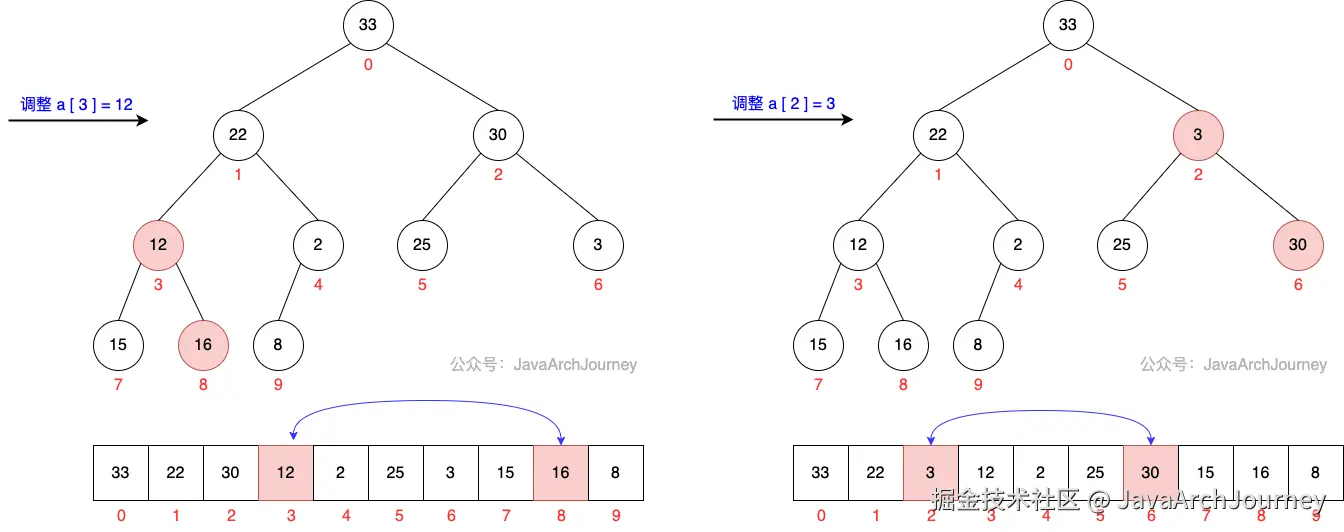
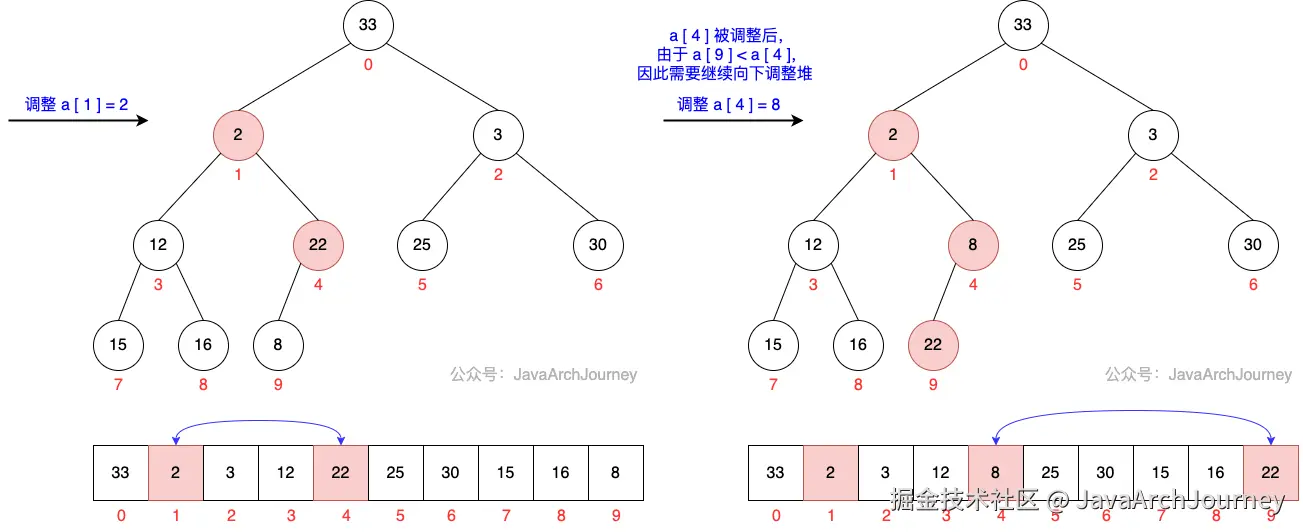
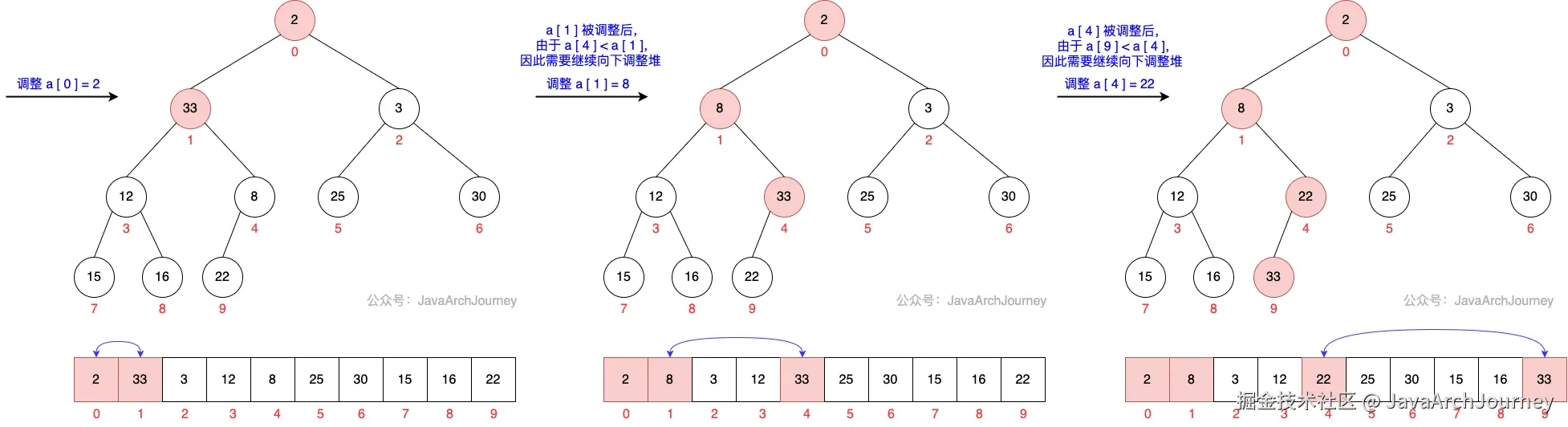
}可以看出,建堆过程是一个从最后一个非叶子节点 开始,自下而上构建最小堆的过程。
建堆过程图示如下:
入队方法
PriorityQueue 通过 offer(E e) 和 add(E e) 方法添加元素到队列中。
java
/**
* Collection 接口方法
*/
public boolean add(E e) {
return offer(e);
}
/**
* Queue 接口方法
*/
public boolean offer(E e) {
// PriorityQueue 不允许存储 null 值
if (e == null)
throw new NullPointerException();
// 修改计数器
modCount++;
// 位置 i 是数组的末尾位置
int i = size;
// 如果当前数组已满,则通过 grow() 方法扩展数组容量
if (i >= queue.length)
grow(i + 1);
size = i + 1;
if (i == 0)
// 如果是第一个元素( i == 0),直接放在数组的第一个位置
queue[0] = e;
else
// 否则,调用 siftUp 方法,将新元素从数组末端向上调整到合适的位置,以保持堆的性质
siftUp(i, e);
return true;
}
/**
* 将新插入的元素向上调整,直到满足堆的性质
*/
private void siftUp(int k, E x) {
// 根据是否存在自定义比较器选择不同的上滤方式
if (comparator != null)
// 使用自定义比较器 Comparator
siftUpUsingComparator(k, x);
else
// 使用自然顺序(元素实现 Comparable 接口)
siftUpComparable(k, x);
}
@SuppressWarnings("unchecked")
private void siftUpUsingComparator(int k, E x) {
// 只要当前节点不是根节点(k > 0),就继续循环
while (k > 0) {
// (k - 1) >>> 1 计算当前节点的父节点索引
int parent = (k - 1) >>> 1;
Object e = queue[parent];
// 对于最小堆:如果新元素 x 比父节点大,则停止
if (comparator.compare(x, (E) e) >= 0)
break;
// 否则,将父节点下移,继续向上调整的过程
queue[k] = e;
k = parent;
}
// 找到正确位置后,将新元素放入该位置
queue[k] = x;
}
@SuppressWarnings("unchecked")
private void siftUpComparable(int k, E x) {
// 逻辑同 siftUpUsingComparator 方法
// 只是使用了 compareTo 方法来进行比较,适用于实现了 Comparable 接口的元素
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = queue[parent];
if (key.compareTo((E) e) >= 0)
break;
queue[k] = e;
k = parent;
}
queue[k] = key;
}
/**
* 对内部数组 queue 进行扩容
*/
private void grow(int minCapacity) {
// 获取当前数组的容量
int oldCapacity = queue.length;
// 计算新容量:
// 1、如果当前容量小于 64:增长为原来的两倍多一点(oldCapacity * 2 + 2)。对于小容量(< 64),增长更快是为了减少频繁扩容带来的性能开销。
// 2、否则:增长为原来的 1.5 倍(通过位移实现)。对于大容量(>= 64),增长放缓(1.5 倍)是为了避免内存浪费。
// Double size if small; else grow by 50%
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// 检查是否超出最大数组长度限制
// overflow-conscious code
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// 使用 Arrays.copyOf() 创建一个新的、更大容量的数组,并复制原有内容
// 实际上是调用了底层的 System.arraycopy()
queue = Arrays.copyOf(queue, newCapacity);
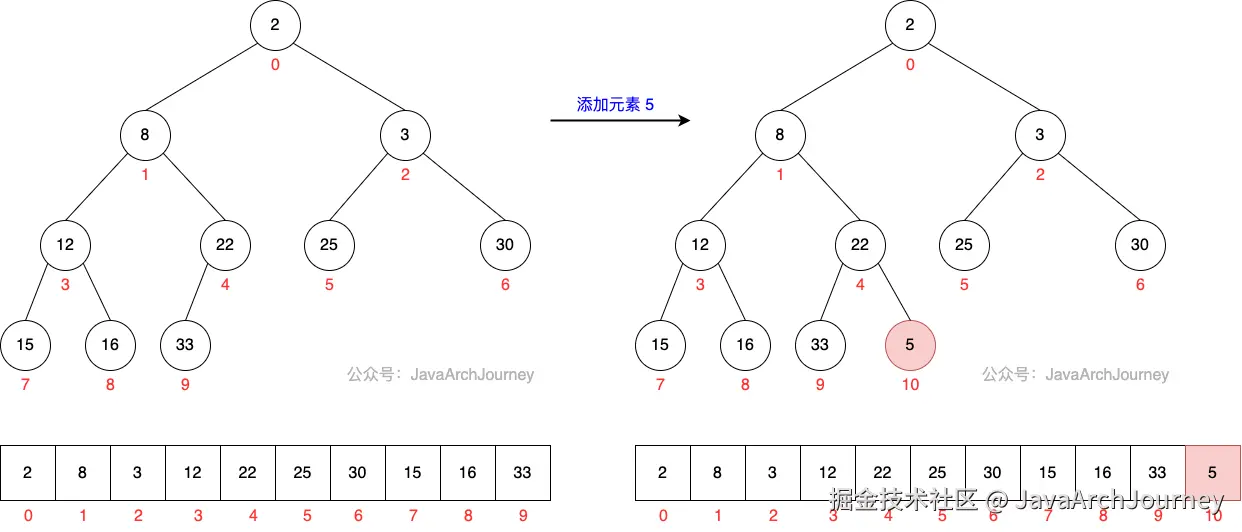
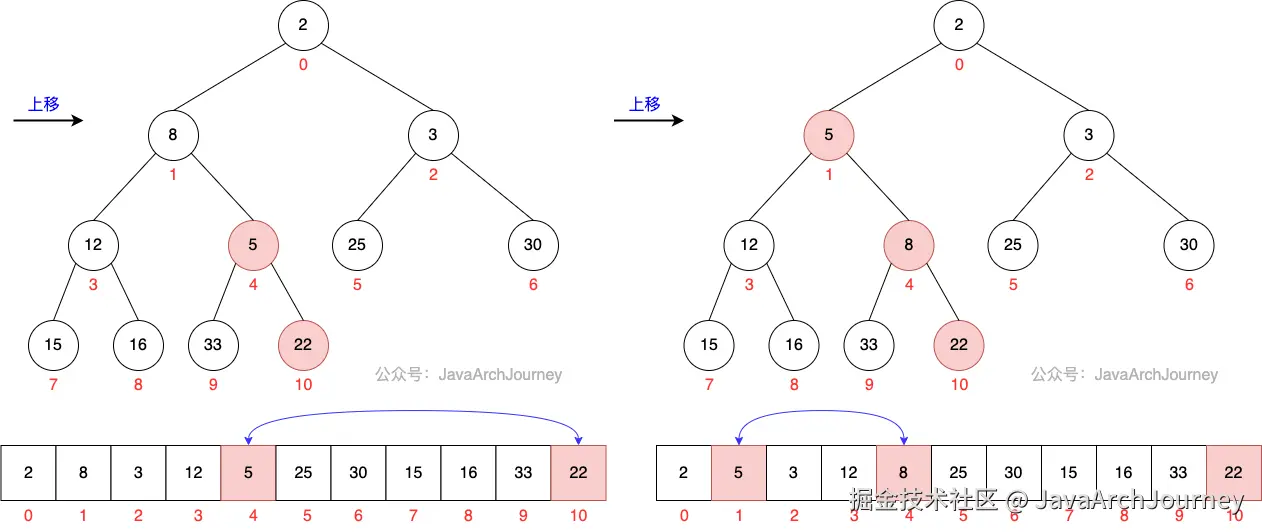
}可以看出,PriorityQueue 入队操作里,元素会先添加到数组末尾,然后通过不断上移以保持最小堆结构。如果在添加过程中发现数组容量不足,会先调用 grow 方法进行数组扩容。
入队过程图示如下:
出队方法
PriorityQueue 通过 poll() 方法移除并返回队列的头元素(最小元素)。如果队列为空,则返回 null。
java
/**
* 删除并返回堆顶元素(即优先级最高的元素)
*/
@SuppressWarnings("unchecked")
public E poll() {
// 如果当前队列为空,直接返回 null
if (size == 0)
return null;
// 减少 size,并保存旧值
int s = --size;
// 修改计数器
modCount++;
// 取出堆顶元素(数组索引为 0 的元素),即最小元素(最小堆)
E result = (E) queue[0];
// 获取最后一个元素,准备用它填补堆顶空位
E x = (E) queue[s];
// 清除最后一个位置的引用,以便GC
queue[s] = null;
// 如果删除后还有元素,则将最后一个元素移到堆顶(索引 0),然后调用 siftDown() 进行下滤调整,确保堆结构不变
if (s != 0)
siftDown(0, x);
// 返回被删除的堆顶元素
return result;
}
private void siftDown(int k, E x) {
// 根据是否存在比较器选择不同的下滤方式
if (comparator != null)
// 使用自定义比较器 Comparator
siftDownUsingComparator(k, x);
else
// 使用元素的自然顺序(通过 Comparable 接口)进行比较
siftDownComparable(k, x);
}
@SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
// 备注:基于完全二叉树的性质,在数组表示中,所有大于 size / 2 - 1 的索引都是叶子节点(这些节点没有子节点)
// half 标识二叉堆最后一个非叶子节点的位置
int half = size >>> 1;
// 只要当前节点不是叶子节点(k < half),就继续循环
while (k < half) {
// 找到当前节点的左右子节点中的较小者
int child = (k << 1) + 1; // (k << 1) + 1:计算左子节点索引
Object c = queue[child];
int right = child + 1;
if (right < size &&
comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right];
// 如果当前节点比这个较小者更小/相等,说明当前子堆已是最小堆,不用继续向下调整,跳出循环
if (comparator.compare(x, (E) c) <= 0)
break;
// 如果当前节点比这个较小者大,则交换两个元素,并更新当前节点索引 k 继续下一轮比较(继续向下调整)
queue[k] = c;
k = child;
}
// 将 x 放在正确的位置上
queue[k] = x;
}
@SuppressWarnings("unchecked")
private void siftDownComparable(int k, E x) {
// 当没有提供比较器时,使用元素自身的 Comparable 接口来进行比较和调整
// 循环逻辑与 siftDownUsingComparator() 基本相同,只是比较的方式不同,使用的是 compareTo() 方法而不是 compare()
Comparable<? super E> key = (Comparable<? super E>)x;
int half = size >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = queue[child];
int right = child + 1;
if (right < size &&
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
c = queue[child = right];
if (key.compareTo((E) c) <= 0)
break;
queue[k] = c;
k = child;
}
queue[k] = key;
}
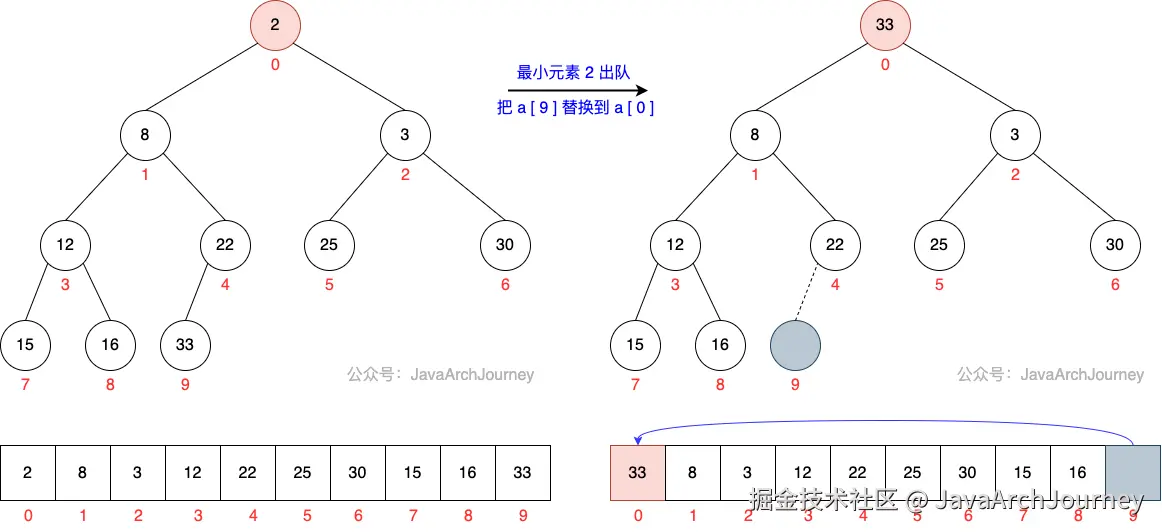
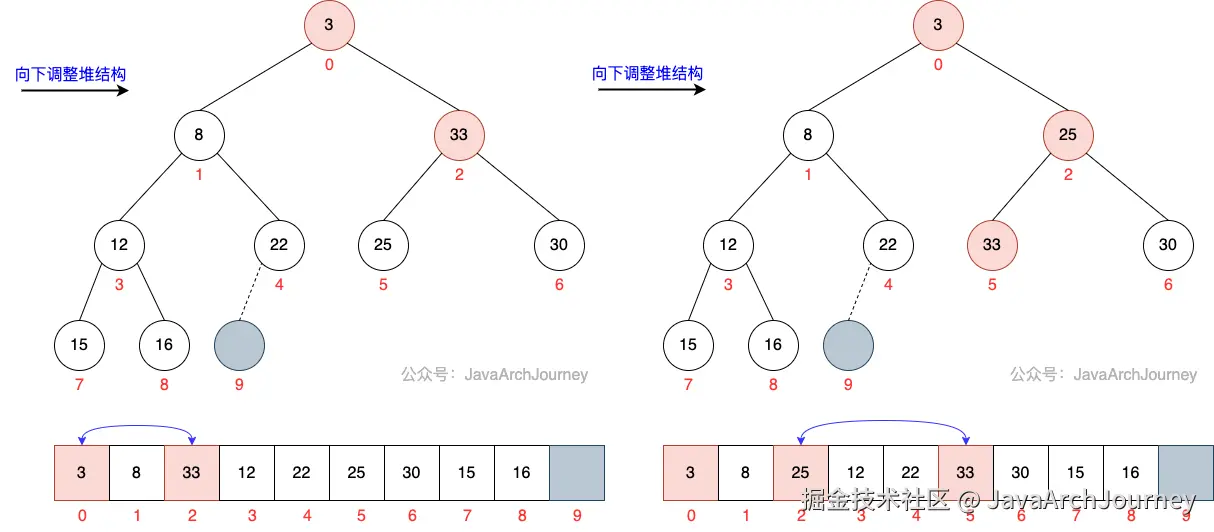
可以看出,出队操作就是移除并返回优先队列中的堆顶元素(即优先级最高的元素),然后将最后一个元素作为替代者移到堆顶,并通过向下重新调整堆以保持其堆性质。
出队过程图示如下:
总结
PriorityQueue通过二叉堆(默认是最小堆)实现的无界优先队列,二叉堆的底层存储结构是数组(Object[] queue)。PriorityQueue不允许元素为null。- 建堆过程 :通过
heapify()方法,从最后一个非叶子节点开始,依次对每个节点执行siftDown()操作,确保每个子树都满足最小堆的性质。时间复杂度为O(n)。 - 入队过程 :在数组末尾添加新元素,然后通过
siftUp()方法将该元素向上调整到合适的位置,以维持堆的顺序。如果数组容量不足,还会调用grow()方法来扩展数组容量。时间复杂度为 O(log n)。 - 出队过程 :移除堆顶元素后,将数组末尾元素移到堆顶,然后使用
siftDown()方法将其向下调整到正确位置。若队列为空,则返回null。时间复杂度为O(log n)。 - 性能特性 :
- 插入和删除操作的时间复杂度是
O(log n)。 - 获取最小元素(队头元素)的操作时间复杂度是
O(1)。
- 插入和删除操作的时间复杂度是