一文搞懂位置编码Positional Encoding

Transformer 架构因其强大的并行能力与建模效果，在自然语言处理和图像理解等领域大放异彩。它的一大特点就是摒弃了传统的 RNN/CNN 顺序结构，转而完全依赖注意力机制。然而，这也带来了一个问题：

没有序列顺序，模型如何知道一个词在句子中的"位置"？

为了解决这个问题，原始 Transformer 在输入 Embedding 中加入了"位置编码（Positional Encoding）"，并采用了一种非常独特的方式 ------ 正弦和余弦函数构造的位置向量。

这篇文章将带你从原理、公式、可视化和优势等多个角度，彻底理解这项设计。

所有相关源码示例、流程图、模型配置与知识库构建技巧，我也将持续更新在Github：LLMHub，欢迎关注收藏！

希望大家带着下面的问题来学习，我会在文末给出答案。

为什么原始 Transformer 要使用正弦和余弦函数来构造位置编码，而不是简单地使用位置索引？
位置编码是"绝对的"，那模型怎么知道两个词之间的相对距离？是否会限制模型的泛化能力？
位置编码向量是固定的数学函数，那模型真的能从中"学会"位置信息吗？它是否会过于僵化？

1. 为什么需要 Positional Encoding？

Transformer 是一个完全并行计算的模型 。不像 RNN/CNN 那样通过结构隐含顺序，它处理输入序列是无顺序感知的。

为了解决这个问题，Transformer 在每个词的表示上添加了一个与它在句中位置有关的向量，也就是 Positional Encoding。

2. 原始公式长啥样？

在原始论文《Attention is All You Need》中，位置编码被定义为如下公式：

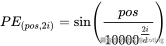
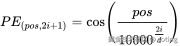
pos：表示该词在句子中的位置（从 0 开始）
i：表示当前维度的位置
d：表示词向量维度

也就是说，对于输入的每个 token（例如第 5 个词），我们遍历维度，对每一个维度使用公式计算出其数值，为其生成一个长度为 d_model 的向量，交替使用 sin 和 cos 来填充奇偶维度。

3.为什么要用正弦函数？

这种设计有多个深意：

3.1多尺度建模能力

通过 10000^{2i/d} 这样的频率控制，sin/cos 的周期从大到小，可以编码不同粒度的顺序信息。低维捕捉长距离位置变化，高维捕捉局部变化。

3.2平滑变化

随着位置 pos 变化，编码向量是连续的，符合自然语言中位置是连续变量的特点。

3.3支持序列泛化

因为是数学函数，位置可以扩展到比训练时更长的序列，而不会像可学习位置编码那样固定在训练长度上。

3.4简单高效

不需要额外学习参数，占用显存小，适合参数紧凑的场景。

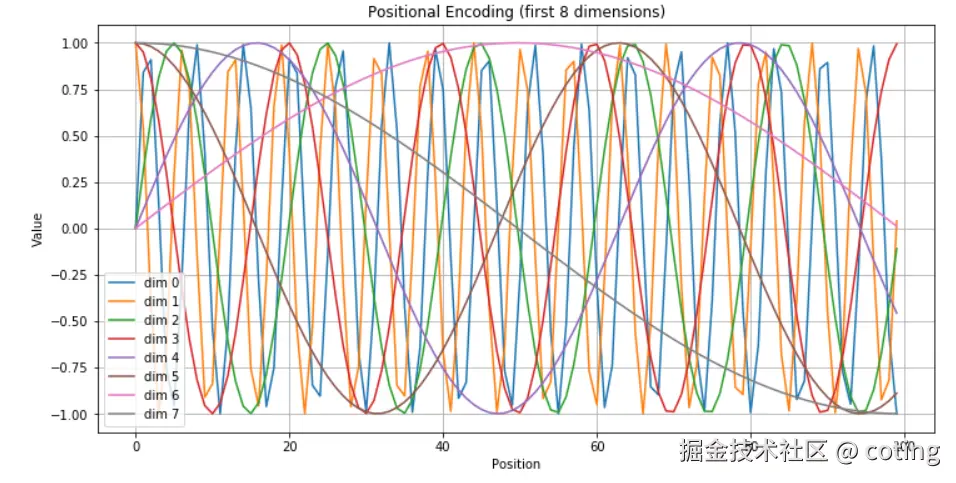
4.可视化：位置编码长啥样？

我们可以绘制前 100 个位置编码在不同维度上的曲线图：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

def get_positional_encoding(seq_len, d_model):
    pos = np.arange(seq_len)[:, np.newaxis]
    i = np.arange(d_model)[np.newaxis, :]
    angle_rates = 1 / np.power(10000, (2 * (i // 2)) / np.float32(d_model))
    angle_rads = pos * angle_rates

    # apply sin to even indices, cos to odd indices
    pos_encoding = np.zeros_like(angle_rads)
    pos_encoding[:, 0::2] = np.sin(angle_rads[:, 0::2])
    pos_encoding[:, 1::2] = np.cos(angle_rads[:, 1::2])
    return pos_encoding

# visualize
pe = get_positional_encoding(100, 16)
plt.figure(figsize=(12, 6))
plt.plot(pe[:, :8])
plt.legend([f"dim {i}" for i in range(8)])
plt.title("Positional Encoding (first 8 dimensions)")
plt.xlabel("Position")
plt.ylabel("Value")
plt.grid(True)
plt.show()

可以得到如下图中一些类似于正弦波的图像，这些波动就是位置信息。

5.Positional Encoding 是怎么用的？

Transformer 中，每个词的最终输入是：

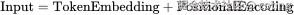
两者直接相加，给词向量注入位置感知能力。

6.有什么缺点？

虽然原始的 PE 简洁有效，但也有一些限制：

缺点	说明
固定函数，缺乏灵活性	无法根据具体任务进行优化
是绝对位置	不考虑 token 之间的相对距离
表达能力弱于学习式编码	在复杂任务上可能不够强

7.后续改进方案有哪些？

方法	特点	应用模型
Learned PE	可学习，更灵活	BERT、GPT-2
Relative PE	编码 token 间的相对位置	Transformer-XL, T5
RoPE	使用旋转矩阵建模相对位置	LLaMA, Grok, GLM
ALiBi	添加 attention bias 表示距离	BLOOM, Falcon

8.总结

原始 Transformer 的 Positional Encoding 是一种简单而有效的机制，它：

使用 sin/cos 编码不同频率的周期信号
为每个词添加绝对位置感知能力
能够支持长序列泛化、计算高效

虽然现代 Transformer 更偏向使用 RoPE 或相对位置编码，但理解原始 Positional Encoding 是学习 Transformer 的基础之一，也是很多架构演进的出发点。

📚 推荐阅读：

《Attention is All You Need》原论文：arxiv.org/abs/1706.03...
Illustrated Transformer

最后，我们回答一下文章开头提出的问题。

为什么用正弦/余弦函数？
因为它们可以以多尺度周期性编码不同的距离变化，且是连续函数，可以外推到未见过的位置，具有良好的泛化能力。简单位置索引无法提供这种连续性和周期层次结构。
绝对位置是否限制了模型？
是的，原始位置编码只表达绝对顺序，不直接提供相对距离信息。这也是后续相对位置编码（如 Transformer-XL、T5）和 RoPE 等改进方案出现的原因。
固定函数是否太僵化？
虽然不可学习，但 Transformer 会通过训练过程自动学会如何"解读"这些编码。这种固定性使模型对长序列有更好的拓展能力。但在某些任务中，确实比可学习位置编码表现略弱。

关于深度学习和大模型相关的知识和前沿技术更新，请关注公众号coting！

所有相关源码示例、流程图、模型配置与知识库构建技巧，我也将持续更新在Github：LLMHub，欢迎关注收藏！