机器学习之K 均值聚类算法

一、聚类算法基础

聚类是机器学习中的无监督学习问题，核心是将相似的数据样本分到同一组，难点在于聚类结果的评估和参数调优。距离度量是聚类的重要基础，常用的有：

欧式距离 ：衡量多维空间中两点的绝对距离，n 维空间公式为各维度差值平方和的平方根。
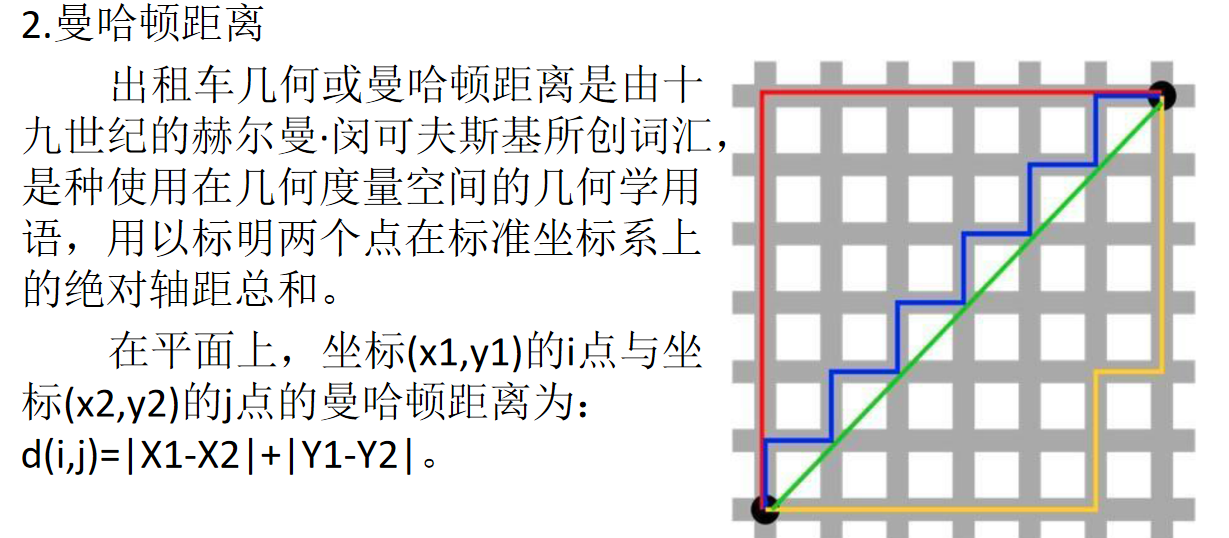
曼哈顿距离 ：计算两点在标准坐标系上的绝对轴距总和，平面上公式为d(i,j)=∣x1−x2∣+∣y1−y2∣。

二、K 均值算法核心

1. 算法步骤

初始化：随机选择 k 个样本作为初始聚类中心。
样本聚类：计算每个样本到各中心的距离，将样本指派到最近中心所属的类。
更新中心：计算每个类中样本的均值，作为新的聚类中心。
迭代收敛：重复步骤 2-3，直到满足停止条件（如中心变化极小或达到最大迭代次数）。

2. 算法评估

CH 指标：通过类内紧密度（类中各点与类中心的距离平方和）和类间分离度（各类中心与数据集中心的距离平方和）评估。CH 值越大，聚类效果越好（类内越紧密，类间越分散）。

3. 优缺点

优点：简单快速，适合常规数据集。
缺点：K 值难以确定；复杂度与样本量呈线性关系；难以发现任意形状的簇。

三、代码实现

1. 相关函数参数

make_blobs()：用于生成聚类数据集，关键参数包括：
- n_samples：数据样本点个数（默认 100）
- n_features：每个样本的特征数（默认 2）
- centers：类别数（默认 3）
- cluster_std：每个类别的方差
- random_state：随机生成器种子（固定数据）
KMeans()：实现 k 均值聚类，关键参数包括：
- n_clusters：分类簇的数量
- max_iter：最大迭代次数
- n_init：算法运行次数
- random_state：随机数生成器种子

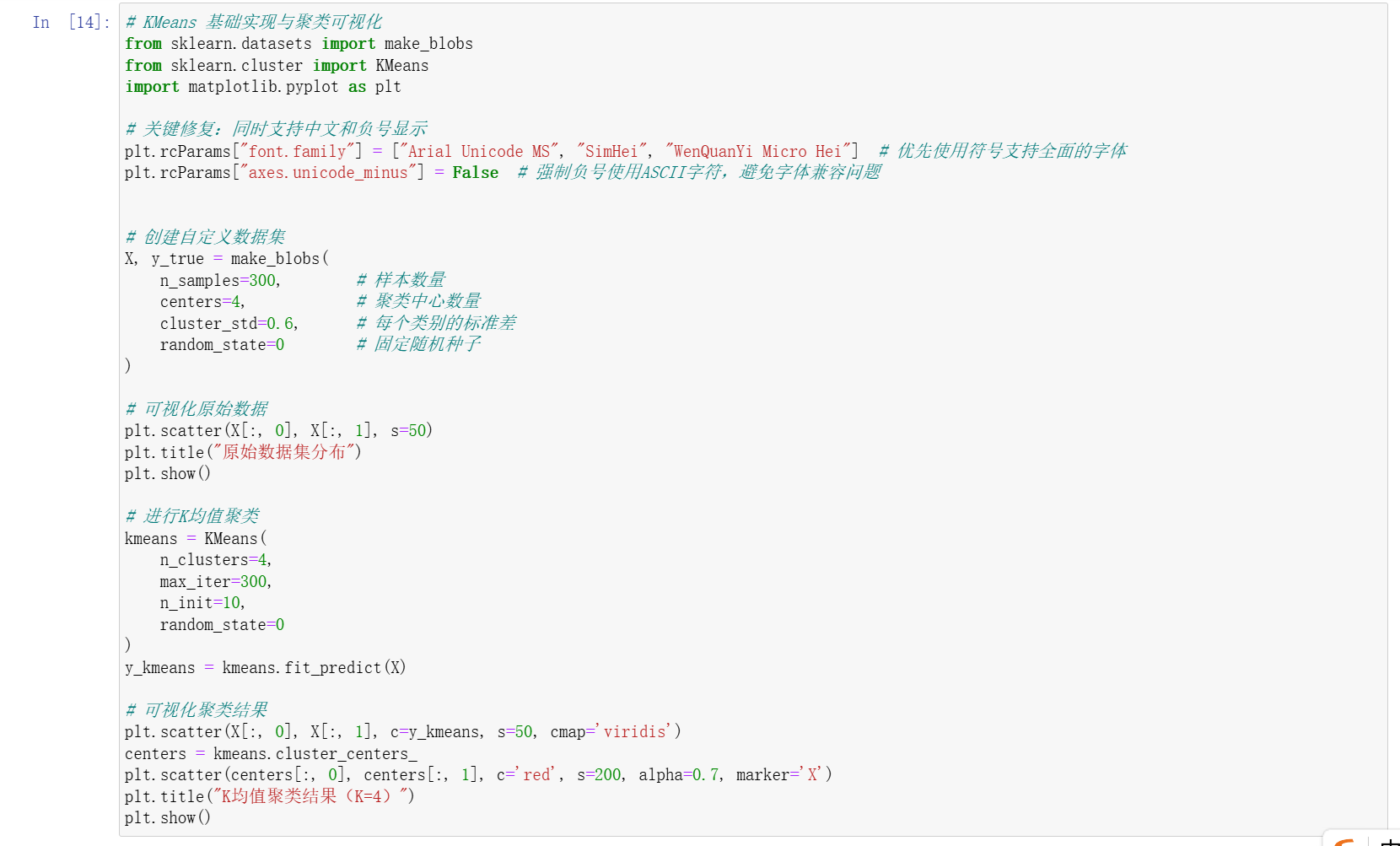
2. 完整代码示例

python

运行

复制代码

# 导入必要的库
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 1. 创建自定义数据集
# 生成300个样本，分为4类，标准差为0.6，固定随机种子
X, y_true = make_blobs(
    n_samples=300,        # 样本数量
    centers=4,            # 聚类中心数量（真实类别数）
    cluster_std=0.6,      # 每个类别的标准差
    random_state=0        # 固定随机种子，保证结果可复现
)

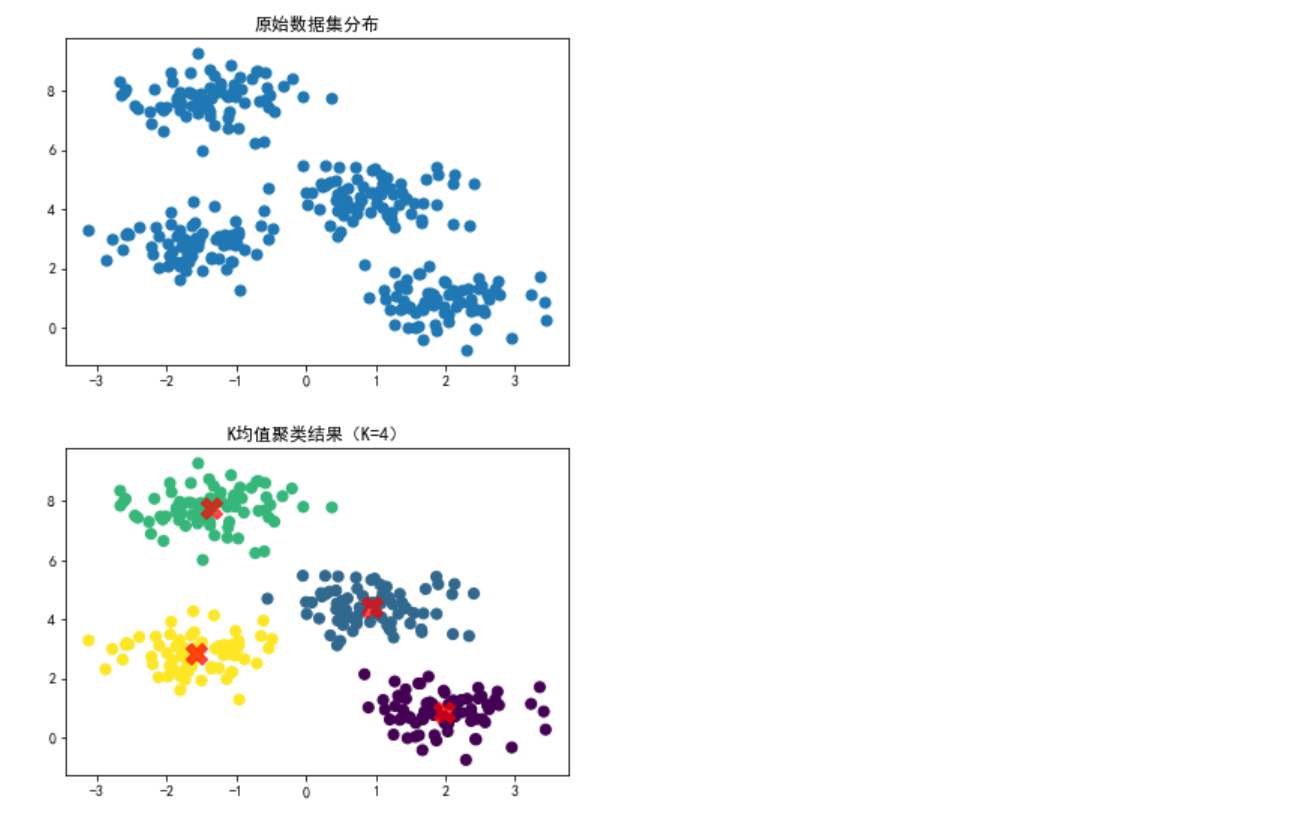
# 2. 可视化原始数据
plt.scatter(X[:, 0], X[:, 1], s=50)  # s为点的大小
plt.title("原始数据集分布")
plt.show()

# 3. 进行K均值聚类
kmeans = KMeans(
    n_clusters=4,         # 指定聚类数量（与真实类别数一致）
    max_iter=300,         # 最大迭代次数
    n_init=10,            # 算法运行次数（取最优结果）
    random_state=0        # 固定随机种子
)
y_kmeans = kmeans.fit_predict(X)  # 拟合模型并预测聚类结果

# 4. 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')  # 用不同颜色标记聚类结果

# 绘制聚类中心
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.7, marker='X')  # 红色X标记中心
plt.title("K均值聚类结果（K=4）")
plt.show()

3. 代码说明

首先使用make_blobs()生成模拟聚类数据，通过参数控制样本量、类别数等。
用散点图可视化原始数据的分布情况。
调用KMeans模型进行聚类，指定聚类数量为 4（与数据生成时的centers一致）。
最后可视化聚类结果，并用红色标记出聚类中心，直观展示算法的聚类效果。

通过本次学习，我掌握了 K 均值算法的基本原理、实现步骤和代码应用，同时理解了其在处理不同数据集时的优势与局限性，为后续更复杂的聚类任务打下了基础。