MySQL--B+树 - 技术栈

扇出为n的n阶B树：每个节点最多存储n-1个key，n个指针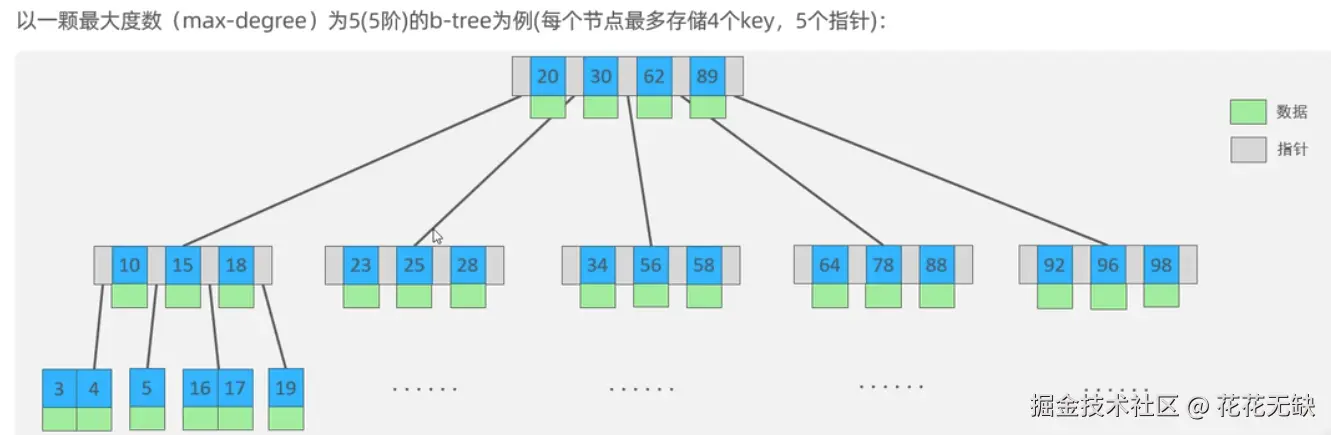扇出为n的n阶B树：每个节点最多存储n-1个索引key，n个指针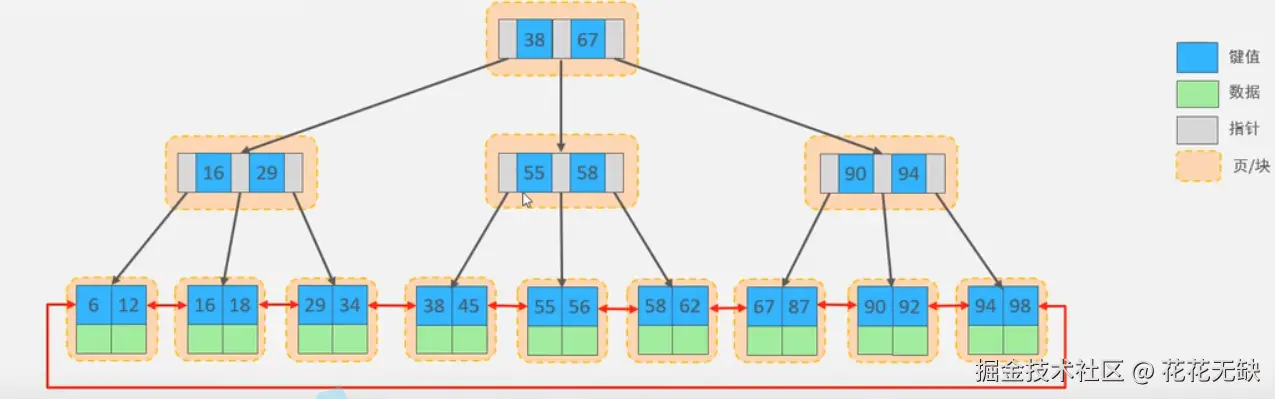

B树（B-Tree）和B+树（B+ Tree）都是平衡的多路搜索树，常用于数据库和文件系统。

1、B树和B+树的区别

数据存储位置：
- B树：数据（键值对）可以存储在内部节点（非叶子节点）和叶子节点上。
- B+树 ：数据只存储在叶子节点上。内部节点仅存储用于导航的索引键（Key）和指向子节点的指针。
叶子节点链接：
- B树：叶子节点之间没有直接的链接。
- B+树：所有叶子节点通过指针形成一个有序的双向链表。这使得范围查询（Range Query）非常高效，只需遍历叶子节点链表即可。
查询效率：
- B树：查找效率不稳定。查找一个存在的键，可能在内部节点就命中，也可能需要查到叶子节点，路径长度不固定。
- B+树：查找效率稳定。任何查找都必须从根节点走到叶子节点，路径长度固定（树的高度），时间复杂度稳定。
空间利用率与扇出：
- B树：由于内部节点也存储数据，每个节点能存储的键/指针对数量相对较少，导致树的"扇出"（每个节点的子节点数）较小，树的高度相对较高。
- B+树：内部节点只存键和指针，不存数据，因此可以容纳更多的键/指针对，扇出更大，树的高度更低。在相同数据量下，B+树通常比B树矮，意味着查询时需要的磁盘I/O次数更少。
范围查询效率：
- B树：进行范围查询时，需要多次从根节点开始查找，效率较低。
- B+树：得益于叶子节点的链表结构，范围查询一旦定位到起始键，就可以顺序遍历链表，非常高效。

2、MySQL（InnoDB引擎）为什么选择B+树？

MySQL的InnoDB存储引擎选择B+树作为其索引结构（尤其是聚簇索引和二级索引），主要原因如下：

高效的范围查询 ：这是最主要的原因之一。数据库应用中范围查询（如 WHERE id BETWEEN 10 AND 100）非常普遍。B+树的叶子节点链表结构使得这类查询只需一次定位起始点，然后顺序扫描即可，性能极佳。
稳定的查询性能： B+树的所有查询（无论是点查还是范围查）最终都落在叶子节点，路径长度固定，性能稳定可预测。
更高的扇出和更低的树高：由于内部节点不存储数据行，可以存储更多的索引键和指针，使得B+树的"扇出"更大。在数据量大的情况下，B+树比B树更矮。这意味着在进行索引查找时，需要的磁盘I/O次数更少（通常只需3-4次I/O就能定位到数据），极大提升了查询效率。磁盘I/O是数据库性能的关键瓶颈，减少I/O至关重要。
全节点扫描效率高：当需要全表扫描或全索引扫描时，B+树可以直接遍历叶子节点的链表，而不需要像B树那样进行复杂的树遍历，效率更高。
更适合磁盘存储特性： B+树的设计更符合磁盘顺序读取的特性。叶子节点的链表结构有利于顺序访问，而内部节点的高扇出减少了随机I/O的次数。

虽然B树在某些特定的点查场景下可能有优势（如果数据恰好在内部节点），但综合考虑范围查询、查询稳定性、I/O效率、全表扫描等数据库核心操作的需求，B+树在绝大多数场景下都优于B树。因此，MySQL（InnoDB）以及其他主流数据库系统（如Oracle, SQL Server）都选择B+树作为其索引结构的基础。

为什么不选择二叉树或红黑树作为索引数据结构？

二叉树 (Binary Tree)

定义：二叉树是一种树形数据结构，其中每个节点最多有两个子节点，分别称为"左子节点"和"右子节点"。

二叉搜索树 (Binary Search Tree, BST) ：这是二叉树的一种重要特例，具有以下性质：

对于任意一个节点，其左子树中的所有节点的值都小于该节点的值。
对于任意一个节点，其右子树中的所有节点的值都大于该节点的值。
左右子树也分别是二叉搜索树。

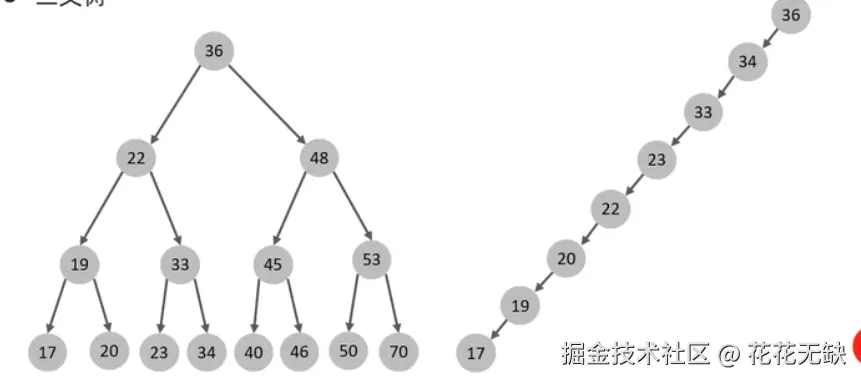
优点：

结构简单，易于理解和实现。
在理想情况下（树是平衡的），查找、插入、删除的时间复杂度为 O(log n)。

缺点：

最大的问题：可能退化成链表。如果插入的数据是有序的（例如，1, 2, 3, 4, 5），二叉搜索树会退化成一个单链表，其高度变为 n，此时查找、插入、删除的时间复杂度退化为 O(n)，失去了树的优势。
不适合磁盘存储：二叉树每个节点只有两个分支，扇出（fan-out）非常小。在存储大量数据时，树的高度会很高，导致查询需要进行大量的磁盘I/O（每次I/O读取一个节点），性能很差。

结论：二叉搜索树不适合用作数据库索引，因为它无法保证平衡性，且扇出太小，I/O效率低下。

红黑树 (Red-Black Tree)

定义：红黑树是一种自平衡的二叉搜索树。它通过在二叉树每个节点上增加一个存储位来表示节点的颜色（红色或黑色），并通过一组严格的规则来确保树在插入和删除操作后仍然保持"大致平衡"，从而保证基本操作的时间复杂度稳定在 O(log n)。

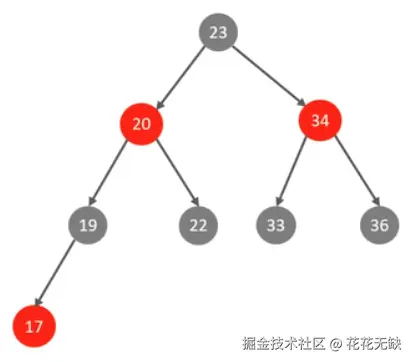
红黑树的五大性质：

每个节点是红色或黑色。
根节点是黑色。
NIL（空）节点是黑色。
如果一个节点是红色的，则它的两个子节点都是黑色的。（即，不能有两个连续的红色节点）
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

优点：

自平衡：通过旋转和变色操作，在插入和删除后自动调整树的结构，防止树变得过于倾斜，保证了 O(log n) 的操作时间复杂度。
效率高 ：对于内存中的数据结构（如Java的 TreeMap, TreeSet），红黑树是非常高效的。

缺点：

仍然是二叉树：虽然自平衡，但每个节点最多只有两个子节点，扇出依然很小。
树的高度相对较高：相比于B树/B+树这种多路平衡树，在存储相同数量的数据时，红黑树的高度会更高。
不适合磁盘存储：由于扇出小、树高，进行数据库查询时需要访问的节点数量多，导致磁盘I/O次数多，性能不佳。

结论：红黑树是一种优秀的内存数据结构 ，广泛应用于各种编程语言的库中。但由于其扇出小、I/O效率低 ，不适合直接用作数据库（如MySQL）的索引结构。数据库索引需要的是能最大化利用磁盘块、减少I/O次数的结构，这就是为什么选择了B+树而不是红黑树。

总结对比

特性	二叉搜索树 (BST)	红黑树 (Red-Black Tree)	B+树 (B+ Tree)
平衡性	不保证，可能退化	自平衡，保证 O(log n)	自平衡，保证 O(log n)
扇出	2（很低）	2（很低）	非常高（可容纳大量子节点）
树高	可能很高（退化时为n）	较高	很低（扇出大）
磁盘I/O	效率极低	效率较低	效率高（核心优势）
范围查询	效率一般（需中序遍历）	效率一般	非常高效（叶子节点链表）
适用场景	小数据量，内存操作	内存中的有序集合（如Java集合）	数据库索引、文件系统

关键点 ：数据库（如MySQL）选择B+树而不是二叉树或红黑树，核心原因是优化磁盘I/O性能。B+树通过高扇出降低了树高，减少了查询所需的磁盘访问次数，并通过叶子节点链表极大提升了范围查询的效率。