3 字符串、数组和广义表(String Array List)
3.1 字符串(String)
3.1.1 串的顺序存储
a. 定长顺序:
c
#define MAXLEN 255
// 串的定长顺序存储结构
typedef struct
{
char ch[MAXLEN + 1]; // 字符串数据,为了方便使用,下标为0的位置不使用。
int length;
} SString;调用示例:
c
SString str1;
str1.length = 5;
str1.ch[1] = 'H'; // 从下标为1的位置开始使用。
str1.ch[2] = 'e';
str1.ch[3] = 'l';
str1.ch[4] = 'l';
str1.ch[5] = 'o';
str1.ch[6] = '\0'; // 结尾字符
printf("SString: %s, Length: %d\n", str1.ch + 1, str1.length); // 输出字符串和长度b. 堆式顺序存储:
c
typedef struct
{
char *ch; // 字符串数据,指向动态分配的内存
int length; // 字符串长度
} HString;调用示例:
c
HString str2;
str2.length = 5;
str2.ch = (char *)malloc((str2.length + 1) * sizeof(char)); // 动态分配空间
if (str2.ch == NULL)
{
printf("Memory allocation failed for HString.\n");
return -1;
}
str2.ch[0] = 'W';
str2.ch[1] = 'o';
str2.ch[2] = 'r';
str2.ch[3] = 'l';
str2.ch[4] = 'd';
str2.ch[5] = '\0'; // 结尾字符
printf("HString: %s, Length: %d\n", str2.ch, str2.length); // 输出字符串和长度3.1.2 串的链式存储
顺序串的插入和删除操作不方便,需要移动大量的字符。 因此, 可采用单链表方式存储串。 由于串结构的特殊性一结构中的每个数据元素是一个字符,则在用链表存储串值时,存在一个 " 结点大小" 的问题,即每个结点可以存放一个字符,也可以存放多个字符。
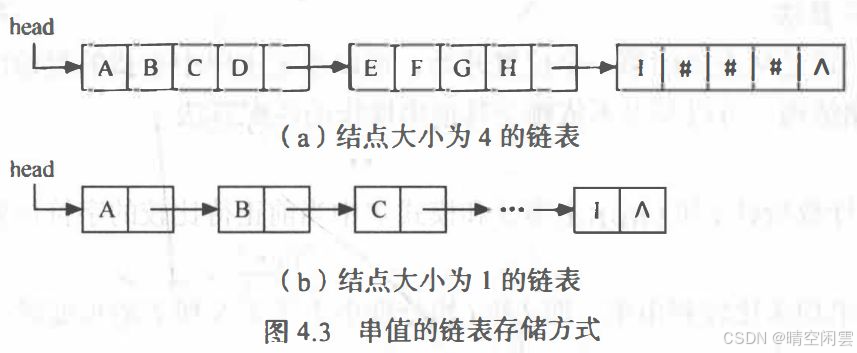
c
// 串的链式存储结构
#define CHUNKSIZE 5 // 每个结点存储的字符数
typedef struct Chunk
{
char ch[CHUNKSIZE]; // 存储字符
struct Chunk *next; // 指向下一个结点
} Chunk;
typedef struct
{
Chunk *head; // 指向第一个结点
Chunk *tail; // 指向最后一个结点
int length; // 串的长度
} LString;书上 CHUNKSIZE = 80,为了方便测试,我修改成了 5。
测试代码:
c
// 示例:创建一个链式存储结构的字符串
LString str3;
str3.length = 0;
str3.head = str3.tail = NULL;
// 假设我们要存储 "Hello string!" 这个字符串,需要分段存储
const char *text = "Hello LString!";
Chunk *currentChunk = NULL;
for (int i = 0; text[i] != '\0'; i++)
{
if (str3.length % CHUNKSIZE == 0) // 每 CHUNKSIZE 个字符创建一个新结点
{
Chunk *newChunk = (Chunk *)malloc(sizeof(Chunk));
if (newChunk == NULL)
{
printf("Memory allocation failed for LString.\n");
return -1;
}
newChunk->next = NULL;
if (str3.head == NULL)
{
str3.head = newChunk; // 第一个结点
}
else
{
str3.tail->next = newChunk; // 尾结点next域指向新结点
}
str3.tail = newChunk; // 尾指针指向新结点
currentChunk = newChunk;
}
currentChunk->ch[str3.length % CHUNKSIZE] = text[i];
str3.length++;
}
if (str3.tail != NULL)
{
currentChunk->ch[str3.length % CHUNKSIZE] = '\0'; // 结尾字符
}
// 输出链式存储结构的字符串
printf("LString: ");
currentChunk = str3.head;
while (currentChunk != NULL)
{
for (int i = 0; i < CHUNKSIZE && currentChunk->ch[i] != '\0'; i++)
{
putchar(currentChunk->ch[i]); // 输出每个结点的字符
}
currentChunk = currentChunk->next; // 移动到下一个结点
}3.1.3 串的模式匹配算法
子串的定位运算通常称 为串的模式匹配或串匹配。字符串有很多相关的算法,书中只介绍了这个算法,就是 Index 这个方法。
书中介绍了两种算法 BF算法 和 KMP算法 进行实现,基于串的定长顺序存储结构实现。
1. BF算法
【算法步骤】
- 别利用计数指针 i 和 j 指示主串 S 和模式 T 中当前正待比较的字符位置, i 初值为 pos,j 初值为 1。
- 如果两个串均未比较到串尾, 即 i 和 j 均分别小于等于S和T的长度时, 则循环执行以下操作:
S[i].ch和T[j].ch比较,若相等,则 i 和 j 分别指示串中下个位置, 继续比较后续字符;- 若不等,指针后退重新开始匹配, 从主串的下一个字符 (
i=i-j+2) 起再重新和模式的第一个字符 (j=1) 比较。
- 如果
j > T.length,说明模式 T 中的每个字符依次和主串S中的一个连续的字符序列相等,则匹配成功,返回和模式T中第一个字符相等的字符在主串S中的序号(i-T.length);否则称匹配不成功,返回0。
【代码实现】
c
// 串的模式匹配算法
int Index(SString S, SString T, int pos)
{
int i = pos, j = 1;
while (i <= S.length && j <= T.length)
{
if (S.ch[i] == T.ch[j]) // 如果当前字符匹配,则i和j都向后移动
{
i++;
j++;
}
else
{
i = i - j + 2; // 回溯到下一个可能的匹配位置
j = 1; // 重置模式串指针
}
}
if (j > T.length) // 完全匹配
return i - T.length;
else
return 0; // 匹配失败
}调用示例:
c
// 示例:串的模式匹配
SString S = { .ch = " ABCDABCD", .length = 8 };
SString T = { .ch = " ABCD", .length = 4 };
int pos = 1; // 从第一个字符开始匹配
int index = Index(S, T, pos);
if (index > 0)
{
printf("Pattern found at position: %d\n", index); // 输出1
}
else
{
printf("Pattern not found.\n");
}
pos = 3; // 从第三个字符开始匹配
index = Index(S, T, pos);
if (index > 0)
{
printf("Pattern found at position: %d\n", index); // 输出5
}
else
{
printf("Pattern not found.\n");
}【算法分析】
a. 最好的情况
每趟不成功的匹配都发生在模式串的第一个字符与主串中相应字符的比较。如下面字符串:
S = "aaaaaba"
T = "ba"设主串的长度为n, 子串的长度为m, 假设从主串的第i个位置开始与模式串匹配成功,则在前 i-1 趟匹配中字符总共比较了 i-I 次;若第 i 趟成功的字符比较次数为 m, 则总比较次数为 i - 1 + m。 对于成功匹配的主串, 其起始位置由 1 到 n-m+I, 假定这 n - m+I 个起始位置上的匹配成功概率相等, 则最好的情况下匹配成功的平均比较次数为
∑ i = 1 n − m + 1 p i ( i − 1 + m ) = 1 n − m + 1 ∑ i = 1 n − m + 1 i − 1 + m = 1 2 ( n + m ) \sum_{i=1}^{n-m+1}p_i(i-1+m) = \frac{1}{n-m+1}\sum_{i=1}^{n-m+1}i-1+m = \frac{1}{2}(n+m) i=1∑n−m+1pi(i−1+m)=n−m+11i=1∑n−m+1i−1+m=21(n+m)
- n-m+1 个位置上的匹配成功概率,因为都相等,所以 p i = 1 n − m + 1 p_i=\frac{1}{n-m+1} pi=n−m+11 。
最好情况下的平均时间复杂度是 O(n + m) 。
b. 最坏的情况
每趟不成功的匹配都发生在模式串的最后一个字符与主串中相应字符的比较。如下面字符串:
S = "aaaaaab"
T = "aab"假设从主串的第 i 个位置开始与模式串匹配成功, 则在前 i - 1 趟匹配中字符总共比较了 ( i − 1 ) × m (i - 1) × m (i−1)×m 次;若第 i 趟成功的字符比较次数为 m,则总比较次数 i × m i × m i×m。 因此最坏情况下匹配成功发的平均比较次数为
∑ i = 1 n − m + 1 p i ( i × m ) = 1 n − m + 1 ∑ i = 1 n − m + 1 i × m = 1 2 m × ( n − m + 2 ) \sum_{i=1}^{n-m+1}p_i(i×m) = \frac{1}{n-m+1}\sum_{i=1}^{n-m+1}i×m = \frac{1}{2}m×(n-m+2) i=1∑n−m+1pi(i×m)=n−m+11i=1∑n−m+1i×m=21m×(n−m+2)
最坏情况下的平均时间复杂度是 O(n × m) 。
2. KMP算法
这个实现的原理咋一听还挺难理解的,视频课程很详细的介绍了 next[j] 的生成,只是感觉没有介绍整体的原理,代码实现上也不太清楚。后来查看网上个一个视频很快就明白了,参考:最浅显易懂的 KMP 算法讲解
next(j) 函数
若令 next[j] = k,则 next[j] 表明当模式中第 j 个字符与主串中相应字符 "失配" 时,在模式中需重新和主串中该字符进行比较的字符的位置。这句话有点难理解,可以参考下图就容易理解了。
比较示例:

next(j) 计算公式:

例如:

关于 next[j]的计算可以参考视频课程,我觉得其中提出的前缀和后缀非常通俗易懂。
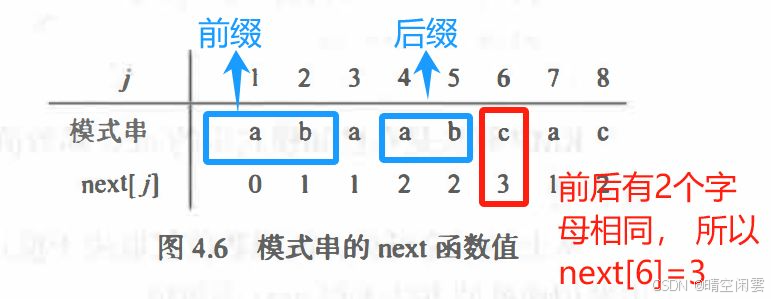
那么为什么可以这么做呢?举上面的图示说明,因为比较到模式串第 6 个字符失配的时候,说明模式串前面 1 ~ 6-1 个字符和对应的主串都相等,即 c 前面 a b 字符和主串对应位置的字符相等,而模式串的前缀是a b,和 c 前面 a b 字符相等,所以可以模式串可以直接从第3个字符 a 开始继续。还是用书中的例子说明:

KMP算法实现:知道KMP的原理后,算法就是在BF算法的基础上做一些改进即可。
c
// Index函数用于查找模式串T在主串S中的位置,使用KMP算法
int Index_KMP(SString S, SString T, int pos)
{
int i = pos; // 主串指针
int j = 1; // 模式串指针
int *next = (int *)malloc((T.length + 1) * sizeof(int));
getNext(T, next); // 获取next数组
while (i <= S.length && j <= T.length) // 两个串均未比较到串尾
{
if (j == 0 || S.ch[i] == T.ch[j]) // 如果当前字符匹配或模式串指针为0,继续比较后继字符
{
i++;
j++;
}
else
{
/* 这里就是改进的地方:i不回溯、模式串向右移动,使用next数组跳过不必要的比较 */
j = next[j];
}
}
free(next); // 释放内存
if (j > T.length) // 完全匹配
return i - T.length;
else
return 0; // 匹配失败
}next函数计算:next函数的计算思路也不好理解,多看书终于get到要点了。

参考书中的示例:

计算 next[7] 和 next[8] 详解如下:
-----------------------------当计算完next[6]时,继续计算next[7]-----------------------------
顺序:1 2 3 4 5 6 7 8
主串:a b a a b c a c // 主串位置为6
字串: a b a a b c a c // 字串位置为3
比较: ≠ // 主串第6个位置的c和字串第3个位置a不相等
字串进行平移,平移的位置就是字串当前位置的next值,即:next[3] = 1
顺序:1 2 3 4 5 6 7 8
主串:a b a a b c a c // 主串位置为6
字串: a b a a b c a c // 字串位置为1
比较: ≠ // 主串第6个位置的c和字串第1个位置a不相等
字串进行平移,平移的位置就是字串当前位置的next值,即:next[1] = 0,值为0,所以 next[7] = 1
-----------------------------当计算完next[7]时,继续计算next[8]-----------------------------
顺序:1 2 3 4 5 6 7 8
主串:a b a a b c a c // 主串位置为7
字串: a b a a b c a c // 字串位置为1
比较: = // 主串第7个位置的a和字串第1个位置a相等
所以 next[8] = 2最终实现代码如下:
c
// KMP算法中获取next数组
void getNext(SString T, int next[])
{
int i = 1; // 主指针
int j = 0; // 子串指针
next[1] = 0; // 初始值
while (i < T.length) // 注意这里的长度是从1开始的,所以i < T.length
{
if (j == 0 || T.ch[i] == T.ch[j]) // 如果前缀指针为0或当前字符匹配
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j];
}
}
}算法分析:KMP算法本身是 O(n),getNext算法是 O(m),综合就是 O(n+m)。
书中还有提到getNext还有一些缺陷, #todo。
3.2 数组(Array)
3.2.1 数组的类型定义
一维数组可以看成是一个线性表,二维数组可以看成数据元素十线性表的线性表。

书中列出了数组常见的操作方法:初始化、销毁、取值、赋值,但是没有具体的实现,这里以二维数组为例进行实现。
1. 初始化
c
// 初始化一个m*n的数组
int **initArray(int m, int n)
{
int **array = (int **)malloc(m * sizeof(int *)); // 分配m个指针
for (int i = 0; i < m; i++)
{
array[i] = (int *)malloc(n * sizeof(int)); // 为每个指针分配n个整数
}
return array;
}2. 赋值
c
// 给数组中的某一个元素赋值
int Assign(int **array, int length1, int length2, int index1, int index2, int value)
{
// 判断是否越界
if (index1 < 0 || index1 >= length1 || index2 < 0 || index2 >= length2)
{
fprintf(stderr, "Index out of bounds\n");
return ERROR;
}
array[index1][index2] = value;
return OK;
}3. 取值
c
// 获取数组中的某个元素
int Value(int **array, int length1, int length2, int index1, int index2)
{
// 判断是否越界
if (index1 < 0 || index1 >= length1 || index2 < 0 || index2 >= length2)
{
fprintf(stderr, "Index out of bounds\n");
return ERROR;
}
return array[index1][index2];
}4. 销毁
c
// 销毁数组
void Destroy(int **array, int length1)
{
for (int i = 0; i < length1; i++)
{
free(array[i]);
}
free(array);
}3.2.2 数组的顺序存储
二维数组可有两种存储方式: 一种是以列序为主序的存储方式; 一 种是以行序为主序的存储方式。
假设每个数据元素占 L 个存储单元, 则二维数组 A[O.. m-1, 0.. n-1] (即下标从 0 开始, 共有m行n列)中任一元素 a i j a_{ij} aij 的存储位置可由下式确定:
L O C ( i , j ) = L O C ( 0 , 0 ) + ( n ∗ i + j ) ∗ L LOC(i, j) = LOC(0, 0) + (n * i + j)*L LOC(i,j)=LOC(0,0)+(n∗i+j)∗L
L O C ( i , j ) LOC(i, j) LOC(i,j) 是 a i j a_{ij} aij 的存储位置; L O C ( 0 , 0 ) LOC(0, 0) LOC(0,0) 是 a 00 a_{00} a00 的存储位置, 即二维数组 A 的起始存储位置,也称为基地址或基址。
由此可以推广到 n 维数组:
L O C ( j 1 , j 2 , . . . , j n ) = L O C ( 0 , 0 , . . . , 0 ) + ( b 2 ∗ b 3 ∗ . . . ∗ b n ∗ j 1 + b 3 ∗ . . . ∗ b n ∗ j 2 + ⋅ ⋅ ⋅ + b n ∗ j n − 1 + j n ) ∗ L = L O C ( 0 , 0 , . . . , 0 ) + ( ∑ i = 1 n − 1 j i ∏ k = i + 1 n b k + j n ) ∗ L LOC(j_{1}, j_{2}, ..., j_{n}) = LOC(0, 0, ..., 0) + (b_{2}*b_{3}*...*b_{n}*j_{1} + b_{3}*...*b_{n}*j_{2}+···+b_{n}*j_{n-1}+j_{n})*L = LOC(0, 0, ..., 0) + (\sum_{i=1}^{n-1} j_{i} \prod_{k=i+1}^n b_{k}+j_{n})*L LOC(j1,j2,...,jn)=LOC(0,0,...,0)+(b2∗b3∗...∗bn∗j1+b3∗...∗bn∗j2+⋅⋅⋅+bn∗jn−1+jn)∗L=LOC(0,0,...,0)+(i=1∑n−1jik=i+1∏nbk+jn)∗L
3.2.3 特殊矩阵的压缩存储
1. 对称矩阵
若 n 阶矩阵A中的元满足下述性质:
a i j = a j i 1 ≤ i , j ≤ n a_{ij} = a_{ji} \quad\quad\quad 1≤i,j≤n aij=aji1≤i,j≤n
则称为n阶对称矩阵。
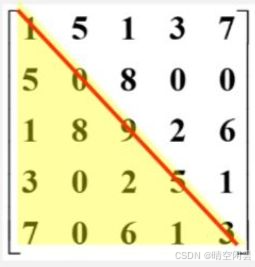
一半的元素个数是:n(n + 1)/2,因此将 n 2 n^2 n2 个元素压缩存储到一维数组 sa[n(n + 1)/2] 中即可。

视频教程 中给出了计算下标 k 思路:
- 行
i:前面有i-1行,等差数列求前面行的元素个数。 - 列
j:所在行前面有j-1个元素,加上自己就是j个元素,
所以下标:k = i(i-1)/2 + j。
书中 罗列了 i >= j 和 i < j 的情况,其实 i >= j 就是下三角、i < j 就是上三角。

关于代码实现,书上和视频教程都没有讲解,我自己写了一下。
对称矩阵的压缩:采用存储下三角部分的方式。
c
// 实现对称矩阵的压缩
// martix 是一个一维数组,表示一个 n*n 的对称矩阵
// n 是矩阵的维度
// compressed 是一个一维数组,用于存储压缩后的数据
// compressedSize 是压缩后的数组大小,用于返回给调用者
Status CompressSymmetricMatrix(int *martix, int n, int **compressed, int *compressedSize)
{
// 假设martix是一个n*n的对称矩阵
// compressed是一个一维数组,用于存储压缩后的数据
if (martix == NULL || n <= 0 || compressed == NULL || compressedSize == NULL)
{
fprintf(stderr, "Invalid input parameters\n");
return ERROR;
}
// 压缩后的数组大小为n*(n+1)/2
*compressedSize = n * (n + 1) / 2;
*compressed = (int *)malloc(*compressedSize * sizeof(int));
if (*compressed == NULL)
{
fprintf(stderr, "Memory allocation failed\n");
return ERROR;
}
// 初始化索引
int index = 0;
// 遍历对称矩阵的下三角部分
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= i; j++)
{
(*compressed)[index] = *(martix + i * n + j);
index++;
}
}
return OK;
}解压缩:解压缩的关键是要求出矩阵的维度n。
c
// 对称矩阵的解压缩
// compressed 是压缩后的数据
// compressedSize 是压缩后的数组大小
// martix 是解压缩后的二维数组
Status DecompressSymmetricMatrix(int **compressed, int compressedSize, int *martix)
{
if (compressed == NULL || compressedSize <= 0 || martix == NULL)
{
fprintf(stderr, "Invalid input parameters\n");
return ERROR;
}
// 计算 martix 的维度 n
int n = 0;
// 第一种方法:通过公式 n*(n+1)/2 >= compressedSize 找到 n
// while (n * (n + 1) / 2 < compressedSize)
// {
// n++;
// }
// 第二种方法:通过一元二次方程求根公式求解。
n = (sqrt(1 + 8 * compressedSize) - 1) / 2; // 这种方法需要包含 <math.h> 库
printf("Decompressing to a %d x %d matrix\n", n, n);
// 初始化索引
int index = 0;
// 遍历对称矩阵的下三角部分
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= i; j++)
{
*(martix + i * n + j) = (*compressed)[index];
if (i != j) // 对称矩阵的上三角部分也需要赋值
{
*(martix + j * n + i) = (*compressed)[index];
}
index++;
}
}
return OK;
}2. 三角矩阵
上三角矩阵是指矩阵下三角(不包括对角线)中的元均为常数c或零的n阶矩阵, 下三角矩阵与之相反。

对三角矩阵进行压缩存储时, 除了和对称矩阵一样, 只存储其上(下)三角中的元素之外, 再加一个存储常数c的存储空间即可,即使用 sa[n(n + 1)/2+1] 的数组存储即可,sa的格式参考如下:
sa[0, 1, 2, 3, ..., n(n + 1)/2]k的下标计算和对称矩阵类似。
上三角矩阵 sa[k] 和 矩阵元素 a i j a_{ij} aij 的对应关系如下:
k = { ( i − 1 ) ( 2 n − i + 2 ) 2 + ( j − i ) 当 i ≤ j n ( n + 1 ) 2 当 i > j k = \begin{cases} \dfrac{(i-1)(2n-i+2)}{2} + (j-i) & \text{当 } i \leq j \\[2mm] \dfrac{n(n+1)}{2} & \text{当 } i > j \end{cases} k=⎩ ⎨ ⎧2(i−1)(2n−i+2)+(j−i)2n(n+1)当 i≤j当 i>j
- 当 i ≤ j i \leq j i≤j,表示是上三角,公式含义分成两个部分: a i j a_{ij} aij 就是 前面 i-1 行元素的个数 加上 第i行中第j个元素前面的元素个数 。
- 第一个部分就是 前面 i-1 行元素的总个数 ,是一个等差求和公式。上三角每行的元素个数:
n-1+1, n-2+1, n-3+1, n-4+1, ... n-i+1, n-n+1,i 从 1 到 n。使用等差数列求和公式即可。
- 第二个部分就是 第i行中第j个元素前面的元素个数 。所以就是
j-i。
- 第一个部分就是 前面 i-1 行元素的总个数 ,是一个等差求和公式。上三角每行的元素个数:
- 当 i > j i>j i>j,表示是下三角,下三角都是一样的元素,存储到这个位置,就是最后一个位置。
下三角矩阵 sa[k] 和矩阵元素 a i j a_{ij} aij 之间的对应关系为:
k = { i ( i − 1 ) 2 + j − 1 当 i ≥ j n ( n + 1 ) 2 当 i > j k = \begin{cases} \dfrac{i(i-1)}{2} + j - 1 & \text{当 } i \geq j \\[2mm] % 公式1 \dfrac{n(n+1)}{2} & \text{当 } i > j % 公式2 \end{cases} k=⎩ ⎨ ⎧2i(i−1)+j−12n(n+1)当 i≥j当 i>j
含义和上三角矩阵类似。
至于代码方面,考虑到和对称矩阵类似,就不再编写了。
3. 对角矩阵
对角矩阵所有的非零元都集中在以主对角线为中心的带状区域中,即除了主对角线上和直接在对角线上、下方若干条对角线上的元之外,所有其他的元皆为零。
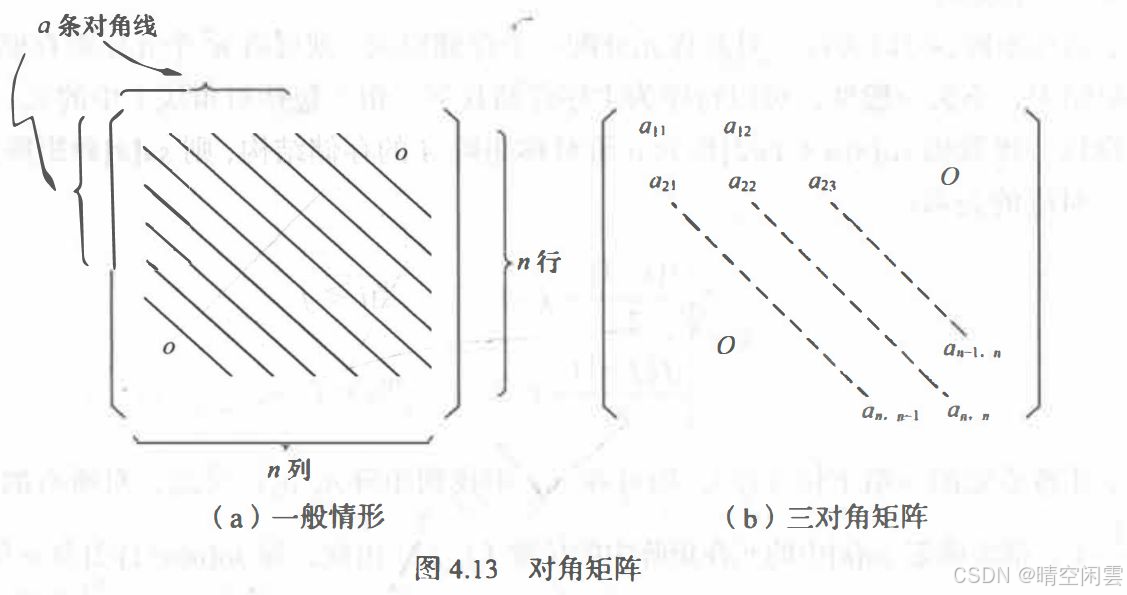
这类矩阵书上没有说明压缩存储的思路,本质上应该还是要找到矩阵行列 i, j 和 数组 sa 下标 k 之间的关系。
4. 稀疏矩阵
书上就是一行带过,含义是其非零元素比较少,且分布没有一定规律。视频教程中提到了可以用三元组进行存储,思路上也非常简单,就不一一尝试了。
3.3 广义表(List)
3.3.1 广义表的定义
广义表是线性表的推广,也称为列表。广泛地用千人工智能等领域的表处理语言LISP语言,把广义表作为基本的数据结构,就连程序也表示为一系列的广义表。
广义表一般记作:
LS = (a1, a2, ..., an)a i a_{i} ai 可以是单个元素,也可以是广义表,分别称为广义表 LS 的原子和子表。
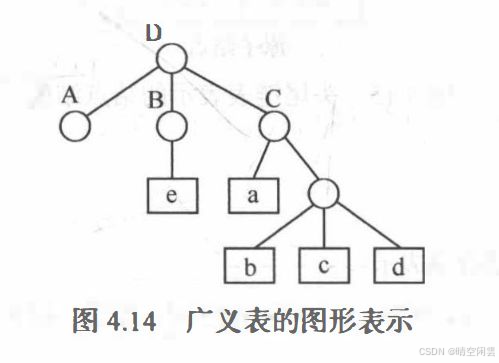
一些例子:
A = ():A 是一个空表, 其长度为零。B = (e):B 只有一个原子 e, 其长度为1。C = (a, (b, c, d)):C 的长度为2,两个元素分别为原子a和 子表(b, c, d)。D = (A, B, C):D 的长度为3, 3个元素都是广义表。显然,将子表的值代入后,则有D = ((), (e), (a, (b,c, d)))。E=(a, E):这是一个递归的表, 其长度为 2。E 相当于一个无限的广义表E=(a,(a,(a, ···)))。
3.3.2 广义表的存储结构
广义表的存储结构常见的有两种:头尾链表的存储结构 和扩展线性链表的存储结构。
1. 头尾链表的存储结构
若广义表不空, 则可分解成表头和表尾, 因此一对确定的表头和表尾可唯一确定广义表。
两种结构的结点:
- 一种是表结点 , 用以表示广义表;
- 表结点可由3个域组成:标志域、 指示表头的指针域和指示表尾的指针域。
- 一种是原子结点 , 用以表示原子。
- 原子结点只需要两个域:标志域和值域。
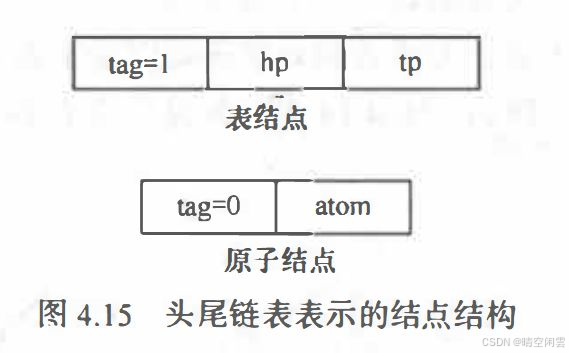
存储结构的代码如下:
c
// 广义表的头尾链表存储表示
typedef enum
{
ATOM,
LIST
} ElemTag; // ATOM==0:原子; LIST==1:子表
typedef struct GLNode
{
ElemTag tag; // 元素类型
union
{
char atom; // 原子元素
struct
{
struct GLNode *hp; // 表头指针
struct GLNode *tp; // 表尾指针
} ptr; // 子表指针
} data;
} GLNode, *GList;前面一小节的提供的例子,用头尾链表存储图示:
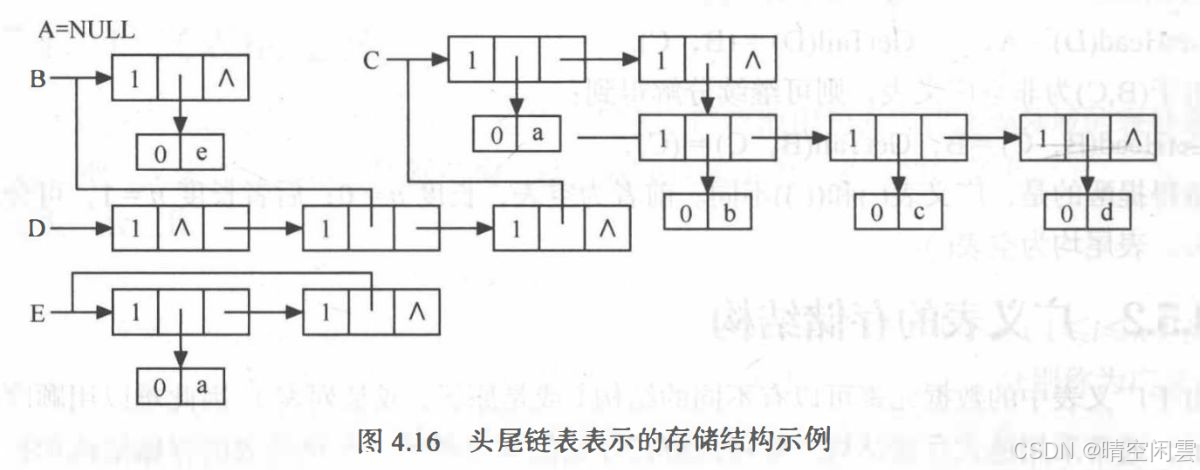
书中和视频都没有相关的代码实现,我想着自己编写一下,一开始想着还挺简单的,实际编写发现坑点还是挺多的,最主要的一个就是每个原子结点都需要要给列表结点包着 ,但是最后参考教程也都解决了,上图的理解是关键。
代码实现了前面一小节的提供的所有广义表例子。因为创建结点要编写很多次,封装成一个方法,方法实现比较简单,不多赘述。
c
// 创建一个新的广义表节点
// 参数 tag 指定节点类型,atom 是原子元素的值,hp 和 tp 分别是表头和表尾指针
// 返回新创建的节点指针
GList CreateNode(ElemTag tag, char atom, GList hp, GList tp)
{
GList newNode = (GList)malloc(sizeof(GLNode));
if (newNode == NULL)
{
fprintf(stderr, "Memory allocation failed\n");
return NULL;
}
newNode->tag = tag;
if (tag == ATOM) // 如果是原子元素
{
newNode->data.atom = atom;
// 这里不能设置 data.ptr.hp 和 data.ptr.tp 为 NULL
// 否则会覆盖掉 data.atom 的值,这个知识点是 union 的特性
}
else // 如果是子表
{
newNode->data.ptr.hp = hp;
newNode->data.ptr.tp = tp;
}
return newNode;
}创建了广义表,总要打印出来看一下,这里也封装了打印的方法:
c
// 打印广义表
// 参数 glist 是广义表的头指针,i 用于控制括号的打印
// 如果 glist 为空,打印 ();如果是原子元素,打印原子值;如果是子表,递归打印表头和表尾
// i 用于控制是否打印开始括号
void PrintGList(GList glist, int i)
{
if (glist == NULL) // 广义表为空
{
printf("()");
return;
}
if (glist->tag == ATOM) // 如果是原子元素
{
printf("%c", glist->data.atom);
}
else // 如果是子表
{
if (i == 0) // 如果是第一个元素,打印开始括号
{
printf("(");
}
// 这里i为什么传0?
// 如果表头指向的元素是 ATOM,那么直接打印对应的原子值,i用不上,没有问题。
// 如果表头指向的元素是 子表,那么它就是子表的第一个元素,所以 i 传递 0。
PrintGList(glist->data.ptr.hp, 0); // 打印表头指向的元素
if (glist->data.ptr.tp != NULL) // 如果表尾不为空
{
printf(",");
i++; // i加1表示这是子表的下一个元素
PrintGList(glist->data.ptr.tp, i); // 打印表尾指向的元素
}
else // 如果表尾为空,意味这是最后一个元素,补上结束刮号
{
printf(")");
}
}
}广义表实现:
c
// 定义一个空的广义表 A
GList A = NULL;
PrintGList(A, 0);
printf("\n");
// 定义广义表 B = (e)
GList B_1_atom = CreateNode(ATOM, 'e', NULL, NULL); // 定义广义表的第1个元素
GList B_1_list = CreateNode(LIST, '\0', B_1_atom, NULL);
GList B = B_1_list; // 将广义表 B 指向第一个元素
PrintGList(B, 0);
printf("\n");
// 定义广义表 C = (a,(b,c,d))
// 因为前面的结点需要指向下一个结点,所以要从后开始往前构造
GList C_2_3_atom = CreateNode(ATOM, 'd', NULL, NULL); // 定义广义表的第2个元素
GList C_2_3_list = CreateNode(LIST, '\0', C_2_3_atom, NULL);
GList C_2_2_atom = CreateNode(ATOM, 'c', NULL, NULL);
GList C_2_2_list = CreateNode(LIST, '\0', C_2_2_atom, C_2_3_list);
GList C_2_1_atom = CreateNode(ATOM, 'b', NULL, NULL);
GList C_2_1_list = CreateNode(LIST, '\0', C_2_1_atom, C_2_2_list);
GList C_2 = CreateNode(LIST, '\0', C_2_1_list, NULL);
GList C_1_atom = CreateNode(ATOM, 'a', NULL, NULL); // 定义广义表的第1个元素
GList C_1_list = CreateNode(LIST, '\0', C_1_atom, C_2);
GList C_1 = C_1_list;
GList C = C_1;
PrintGList(C, 0); // 打印 (a,(b,c,d))
printf("\n");
// 定义广义表 D=(A,B,C)
GList D_3_list = CreateNode(LIST, '\0', C, NULL); // 将 C 作为表头
GList D_2_list = CreateNode(LIST, '\0', B, D_3_list); // 将 B 作为表头
GList D_1_list = CreateNode(LIST, '\0', A, D_2_list); // 将 A 作为表头
GList D = D_1_list; // 将 D 指向第一个元素
PrintGList(D, 0); // 打印 (A,B,C)
printf("\n");
// 定义广义表 E = (a,E)
GList E_1_atom = CreateNode(ATOM, 'a', NULL, NULL); // 定义广义表的第1个元素
GList E_1_list = CreateNode(LIST, '\0', E_1_atom, NULL);
GList E_1 = E_1_list;
GList E_2 = CreateNode(LIST, '\0', E_1, NULL); // 将 E_1 作为表头
E_1->data.ptr.tp = E_2; // 将 E_2 作为表尾
GList E = E_1; // 将 E 指向第一个元素
PrintGList(E, 0); // 打印 (a,E),实际一直打印(a,(a,(a,(a,...2. 扩展线性链表的存储结构
无论是原子结点还是表结点均由三个域组成:

和头尾链表的存储结构不同的是,因为原子结点也有尾指针,因此可以直接指向下一个结点。如下图:
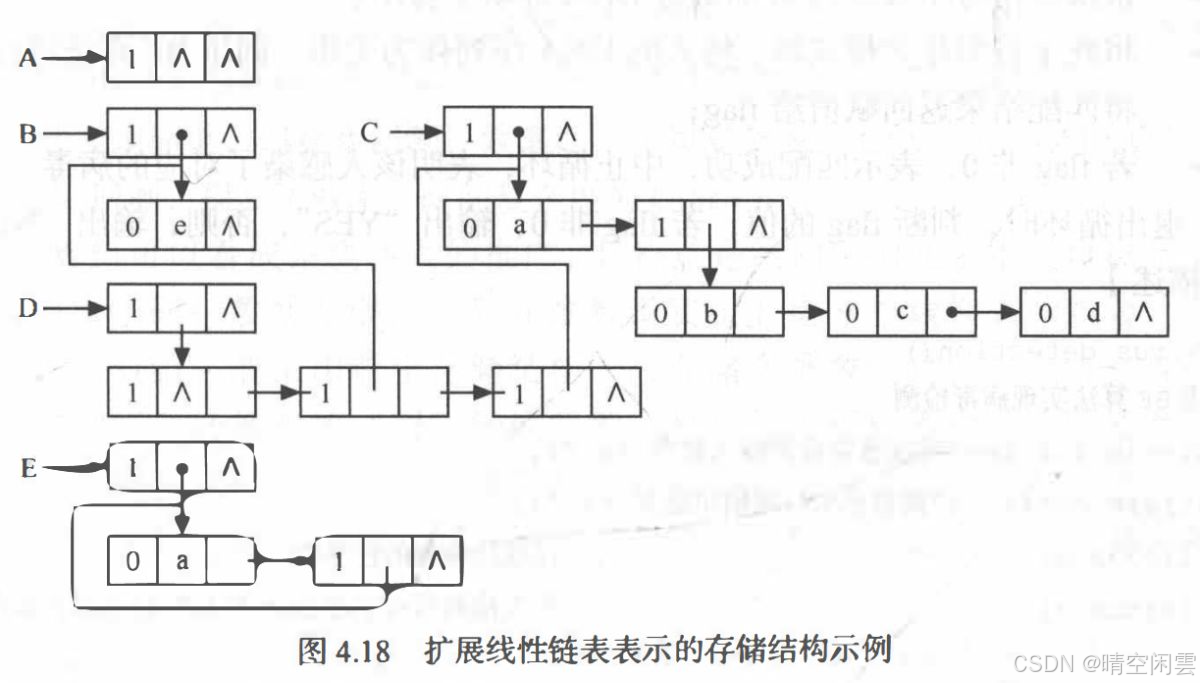
从图示上来看,这种结构明显会比前面的一种方式更加简单,因为原子结点多出了一个 tp 指针指向下一个元素,就不用再用一个表结点包裹着了。
先定义广义表扩展线性链表的存储结构,和前面一种方式大同小异,就是可以表尾指针提取到最外层,原子结点和表结点都有表尾指针。
c
typedef enum
{
ATOM,
LIST
} ElemTag; // ATOM==0:原子; LIST==1:子表
typedef struct GLNode
{
ElemTag tag; // 元素类型
union
{
char atom; // 原子元素
struct GLNode *hp; // 表头指针
} data;
struct GLNode *tp; // 表尾指针
} GLNode, *GList;创建新结点:
c
// 创建一个新的广义表节点
// 参数 tag 指定节点类型,atom 是原子元素的值,hp 和 tp 分别是表头和表尾指针
// 返回新创建的节点指针
GList CreateNode(ElemTag tag, char atom, GList hp, GList tp)
{
GList newNode = (GList)malloc(sizeof(GLNode));
if (newNode == NULL)
{
fprintf(stderr, "Memory allocation failed\n");
return NULL;
}
newNode->tag = tag;
if (tag == ATOM) // 如果是原子结点
{
newNode->data.atom = atom;
}
else // 如果是表结点
{
newNode->data.hp = hp;
}
newNode->tp = tp;
return newNode;
}打印广义表 这块麻烦一些,主要就是要厘清什么时候打印结束刮号。
c
// 打印广义表
// 参数 glist 是广义表的头指针
// 如果 glist 为空,打印 ();如果是原子元素,打印原子值;如果是子表,递归打印表头和表尾
void PrintGList(GList glist)
{
if (glist == NULL) // 广义表为空
{
printf("()");
return;
}
// 1. 如果是原子结点
if (glist->tag == ATOM)
{
printf("%c", glist->data.atom);
if (glist->tp != NULL) // 如果表尾不为空
{
printf(",");
PrintGList(glist->tp); // 打印表尾指向的元素
}
return;
}
// 2. 如果是表结点
printf("("); // 只要是表结点,就打印开始括号
int endFlag = 0; // 用于标记是否已经打印过结束括号
if (glist->data.hp != NULL) // 如果表头不为空
{
PrintGList(glist->data.hp); // 打印表头指向的元素
// 如果表头指向的元素是原子结点,并且该原子结点的表尾为空,则表明包裹该原子结点的表已经结束。
if (glist->data.hp->tag == ATOM && glist->data.hp->tp == NULL)
{
endFlag = 1; // 设置结束标志
printf(")");
}
}
else // 如果表头为空,意味着是一个空表,直接打印结束符号
{
endFlag = 1; // 设置结束标志
printf(")");
}
if (glist->tp != NULL) // 如果表尾不为空
{
printf(",");
PrintGList(glist->tp); // 打印表尾指向的元素
}
if (!endFlag) // 如果前面没有打印过结束括号
{
printf(")");
}
}定义A、B、C、D、E五个 广义表,这个就比前一种方式简单多了。
c
// 定义一个空的广义表 A
GList A = CreateNode(LIST, '\0', NULL, NULL);
PrintGList(A);
printf("\n");
// 定义广义表 B = (e)
GList B_1_atom = CreateNode(ATOM, 'e', NULL, NULL); // 定义广义表的第1个元素
GList B = CreateNode(LIST, '\0', B_1_atom, NULL); // 定义广义表的第1个子表
PrintGList(B);
printf("\n");
// 定义广义表 C = (a,(b,c,d))
GList C_2_3_atom = CreateNode(ATOM, 'd', NULL, NULL); // 定义广义表的第2个元素:(b,c,d)
GList C_2_2_atom = CreateNode(ATOM, 'c', NULL, C_2_3_atom);
GList C_2_1_atom = CreateNode(ATOM, 'b', NULL, C_2_2_atom);
GList C_2 = CreateNode(LIST, '\0', C_2_1_atom, NULL);
GList C_1_atom = CreateNode(ATOM, 'a', NULL, C_2); // 定义广义表的第1个元素:a
GList C = CreateNode(LIST, '\0', C_1_atom, NULL); // 定义广义表 C
PrintGList(C);
printf("\n");
// 定义广义表 D=(A,B,C)
GList D_3 = CreateNode(LIST, '\0', C_1_atom, NULL); // D 的第3个元素是 C
GList D_2 = CreateNode(LIST, '\0', B_1_atom, D_3); // D 的第2个元素是 B
GList D_1 = CreateNode(LIST, '\0', NULL, D_2); // D 的第1个元素是 A
GList D = CreateNode(LIST, '\0', D_1, NULL); // 定义广义表 D
PrintGList(D); // 打印 D
printf("\n");
// 定义广义表 E = (a,E)
GList E_2 = CreateNode(LIST, '\0', NULL, NULL); // 定义广义表的第2个元素 E
GList E_1_atom = CreateNode(ATOM, 'a', NULL, E_2); // 定义广义表的第1个元素 a
GList E = CreateNode(LIST, '\0', E_1_atom, NULL); // 定义广义表 E
E_2->data.hp = E_1_atom; // 将 E_2 指向 E 本身,形成循环
PrintGList(E); // 打印 (a,E),实际一直打印(a,(a,(a,(a,...