仅供个人复习
1.kmp算法
对于匹配串(长一点的那个),其在匹配过程中i指针不发生回溯只有向前
对于模式串(要在匹配串中找到的串叫做模式串)
如何构造next数组
我们对于一个串"aabaab"进行构造,我们默认next数组从1开始记号
我们默认next数组1 和2都直接填0和1
我们直接从第三个位置开始构造
当我们构造第三个元素"b"的next数组我们可以这样看
我们就看第三个元素前面的所有元素构成的串是什么样
前缀:除了最后一个字符以外的所有字符串组成
后缀:除了第一个字符意外的所有字符串组成
前缀:{a}
后缀:{a}
匹配了一个a,该串长度为a
所以3处填写1+1=2
对于第四个位置,我们看前三个位置
前缀:{a,aa}
后缀:{b, ab}
无匹配
所以4处填写1+0
对于第五个位置
前缀:{a,aa,aab}
后缀:{a,ab,aba}
1+1=2
对于第六个位置
前缀:{a,aa,aab,aaba}
后缀:{a,aa,baa,abaa}
所以第六个位置
1+2(最长的匹配串)=3
|--------------|---|---|---|---|---|---|
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| next数组内容 | 0 | 1 | 2 | 1 | 2 | 3 |
| nextval | 0 | 0 | 2 | 0 | 0 | 2 |
| 串的内容记为s[j] | a | a | b | a | a | b |
改进后的nextval数组的内容只需要看,当指向模式串的最高位的j指针回溯后指向的元素是否还和原来相同即可
如果相同则nextval[j]=next[next[j]]直到nextval[j]里的元素不同于s[j]
比如第二个位置的next指向1这个位置的元素,但这两个元素同样是a,所以nextval里的数据就会找到原本next指向的位置的next的内容,即找到原本next指向的是1,我们发现s[1]=a=s[j=2]所以我们会将next[1]里的数据填充到nextval[j]中
具体看王道书117页
计算滑动了多少位置只需要用j-next[j]
如果使用nextval那么就只需要计算j-nextval[j]
1.树
树中一个孩子的分支的个数称为节点的度
树中最多度的孩子的度被称为树的度
边,两个结点之间相连接的一个线段就叫做边
路径长度:经过多少条边
树的节点数n:等于所有节点的度数之和+1(每一度就代表有一个节点被唯一指向,除了根节点每个节点都会被唯一一个度指向)
高度为h的m叉树:
1.在第h层最多有m^(h-1)个节点
2.总共有1+m+m².........m^(h-1)=等比数列求和公式
度为m,具有n个节点的树最小高度计算方法:
(前h-1层的节点数总和,等比数列求和公式)<n<=
(h高度的树最多可能的节点数)
然后开logm次方进行h的计算即可
度为m,具有n个节点的树最大高度计算方法:
除了最后一个非叶子节点外,其余节点度数都为1
有h-1(除了叶节点那一层前面的所有层)+m=n
推导得到h=n-m+1
2.二叉树
对于一颗完全二叉树来说,最后一个分支节点为n/2向下取整
若i>n/2则为叶节点
假定节点总数为n 度数为1或者2的结点为
有如下结论
1.节点总数为n=n1+n2+1。 证明:若一个节点有一个孩子则会产生一个分支,即一个节点会被一个分支所指向,除了根节点之外。那么,度数为1的节点其就对应了一个分支,度数为2的节点就对应了2个分支,所以n1+2n2就等于所有所有的被指向的节点(除了根节点外)所以需要加上1
2.假定一节点编号为[n/2]向下取整,若i<=[n/2]向下取整的都是分支节点,否则为叶节点
3.若某节点的编号为i且其只有左孩子或者为叶节点,则编号大于i的节点都是叶节点
4.若n为奇数,则每个分支节点都有左右孩子,若为偶数则最大的那个分支节点(即n/2)只有左孩子,因为根节点只有一个,对于二叉树来讲,n=n1+2n2+1 因为2n2必定为偶数,则n若为奇数则2n+1必为奇数,也就是说n1=0同理可证n为偶数的情况
5.当i>1时,其双亲节点为[i/2]向下取整
6.节点i所在的深度为[log2i]向下取整+1
7.n0=n2+1 由n0+n1+n2=2n2+n1+1推导得出
8.对于一个二叉链表存储的二叉树,若总共又n个节点,那么其有2n个指针域,其中n个结点除了头结点以外,每个节点都会被一个指针所指向,共有n-1个指针域被使用,所以空指针域为2n-(n-1)=n+1

卡特兰数

堆排序的构建和删除的比较过程
当插入新元素:一路向北进行比较
当删除元素时:一路向南进行比较
当调整堆时:给定一个序列,从后往前数第一个分支节点开始比较,然后数组下标一路往前找分支节点,比较前面的分支节点,即从序列第一个分支节点一路向前调整
构建堆时:一旦发生了违反堆规则的序列就直接调整
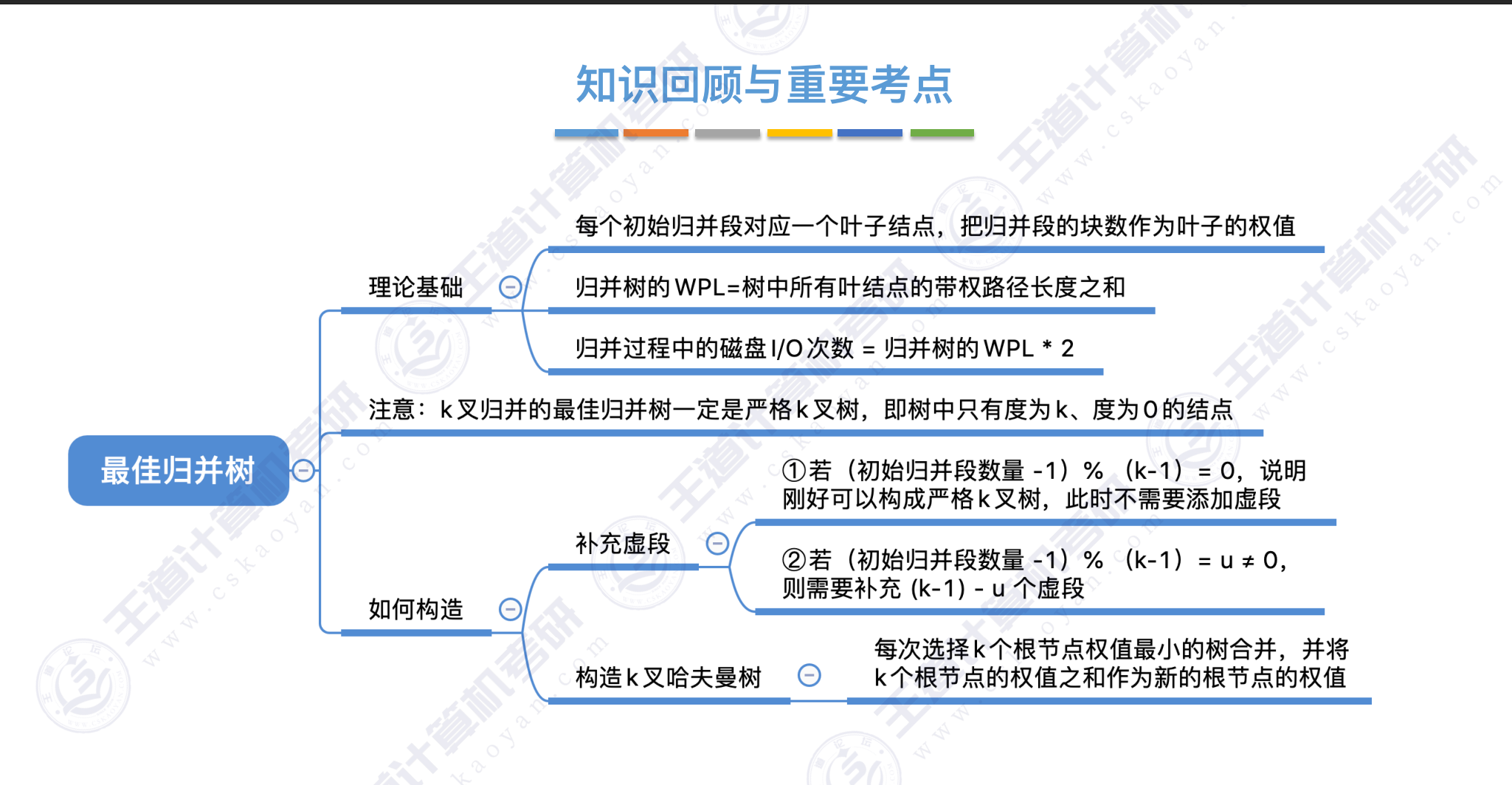
k叉归并树能否严格构成
下图的公式
补充的归并段
以及是否需要补充是重点
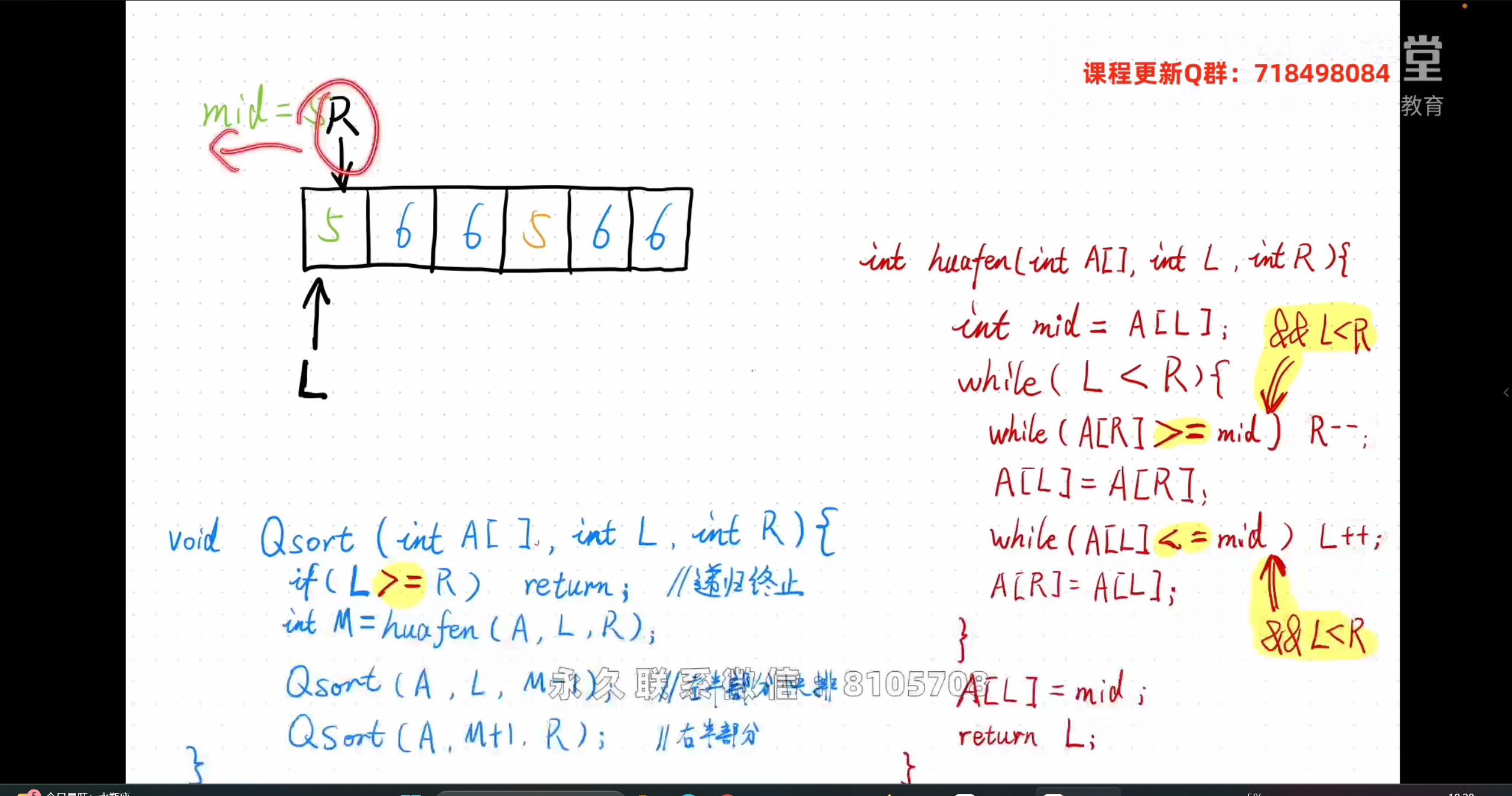
快排模板