引言
好几天前看的华为杯24年C题的优秀论文,在前一篇文章也提供了下载方法或者网盘地址,整体看下来每一篇都各有千秋,都有值得借鉴的地方,作为竞赛论文来说整体性和完善性都配的上优秀论文(佩服佩服,我啥时候能写成这样呜呜,哈哈哈)。这篇文章主要想就第五问的优化问题总结一下这几篇文章的针对双目标优化问题的处理方法及常用算法。
正文
问题重述

题目要求磁芯损耗最小,这个是问题二和问题四相关的模型(对于问题四个人感觉可以对问题二的模型再加以修正,并通过深度学习等模型辅助验证,也就是问题四最后的模型最好为机理模型,而非深度学习模型,如果问题四直接上机器学习则与第五问连贯性不太好),并且传输磁能最大,这个直接给出了计算公式,前面问题并未涉及。需要注意的是温度、波形、磁芯材料均为离散变量。
优秀论文C24102890089 :在问题四中对于磁芯损耗的预测通过对问题二中的模型加以简单修正,列表给出了具体模型及其精度和预测结果,对于第五问主要思想是将双目标转化为单目标,结合第四问中的模型,并将温度变量转化为了连续变量,文中提到常见的转化方法为:加权和法、理想点法、ϵ-约束法双目标转化为单目标方法介绍,文中采用的是比值法(如图所示)P为损耗,Q为传输磁能
优秀论文C24103860012 :问题四的思路如下图,前面的机理模型验证不理想后使用机器学习完成了第四题,后面画的雷达图感觉还不错就截过来了
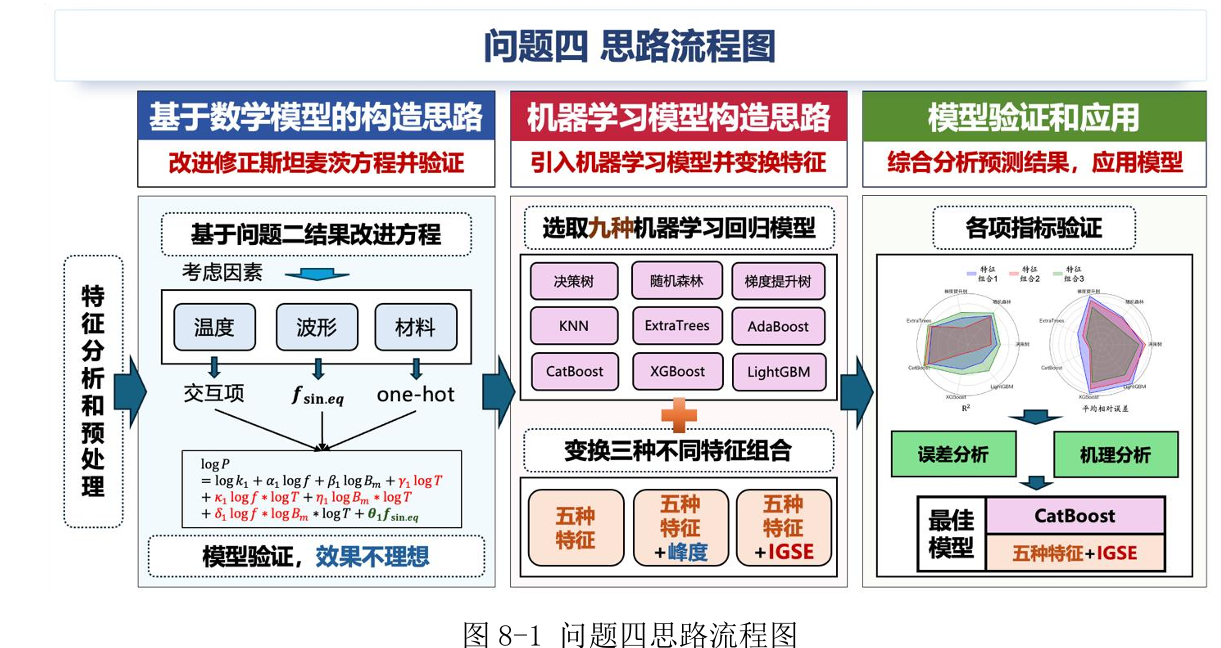
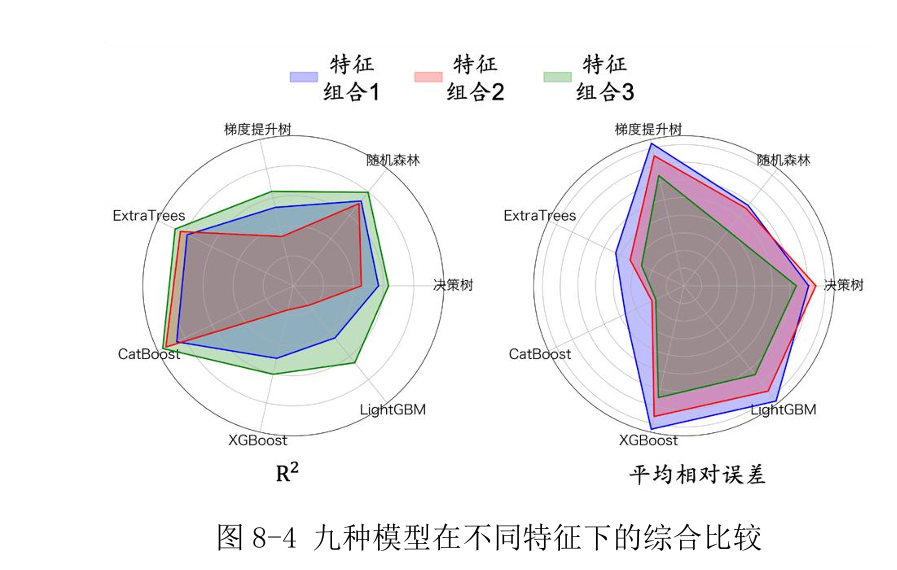
针对第五题,文中使用权重法(两个目标函数权重相同)将双目标转化为单目标,优化算法使用了遗传算法、粒子群、灰狼算法,问题三的分析固定了离散变量或对离散变量分类讨论,理论上可以比较三种算法对于同一个目标函数的最值情况,但本文在最后算法生成的最优解之前引入了两个评价指标 (如下图所示,可能是pdf阅读器的原因公示显示不全)来确定最终的解,这一点让人感觉更综合、更全面,有一种正确答案的感觉,文中也详细介绍了三种算法的实现步骤并给出了遗传算法和灰狼的算法示意图。
优秀论文C24106130096 :在第四问中提出了深度自表示方法,可以有效地将深度学习模型与传统模型相结合,在处理第五问是对于双目标转化为单目标的方法用了以下两种,其中减法模型设置了五种惩罚系数,为什么这样做设置数值也感觉缺乏一定的说明,二者的约束条件都相同,变量包含离散和连续变量:

智能优化算法使用了遗传算法、粒子群,对于两种算法的介绍更详细。
优秀论文C24104220149 :在问题四中提出了双向LSTM算法,针对第五问的模型构建如下图,不同于其他三篇文章的目标转化,本文中将两个目标函数的权重系数作为决策变量求解 ,文中也提到对于两个目标题目没有明显偏好,因此处理方法比较开放,但是对于权重视为决策变量不知理论依据是什么,其中单目标使用了遗传算法和单目标粒子群,并对原双目标问题使用NSGA-II,双目标粒子群,上述算法都有实施步骤说明或者结构图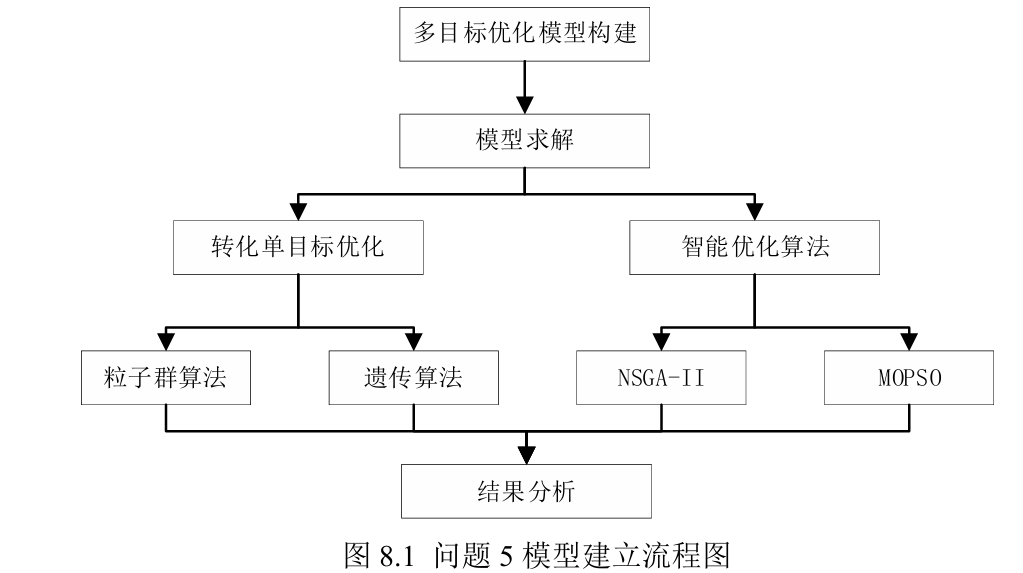
总体来看这个第五问使用的模型不少,也很全面,但是感觉在结果上少了什么东西。
结语和代码
正如在引言中所述C题的四篇论文都各有千秋,对于多目标优化问题的处理手段让人眼前一亮,比如根据实际问题设置新的评价指标、将权重系数作为决策变量等等,其中也有很多细节值得深入探讨学习。
对于算法方面,这几篇文章几乎都使用了粒子群算法和遗传算法,当然每篇文章对于变量的处理手段不尽相同,具体来说有一篇文章将所有的的分类变量根据前面问题的讨论都给剔除或者分类建立模型,这样做也是每一种分类情况都是比较清晰的,如果不这样做算法本身也是支持分类变量的(应该是这样的,我没有查到具体的资料)。 附录方面优秀论文C24106130096 和优秀论文C24103860012 让人看得更加舒服(有边框,除了代码还有其他介绍,字号方面等等),我都截图在下面,顺便说一下文中也有说明运行代码的计算机信息等等。


对于两种算法的详细理论知识及实践过程可以参考论文中的描述或B站上的视频,对于单目标粒子群算法,数学建模清风老师更新中有讲解,并且提供了多种改进算法的matlab代码。另外还有一个值得探究的问题就是无论是将双目标转化为单目标还是直接双目标的算法,两个目标都应该是一个函数,但是像论文中提到如果一个目标是深度学习模型,比如最简单的前馈神经网络,后续处理的代码具体应该是怎样的?下面给出多目标的粒子群和NASA-II的python代码,
python
###多目标粒子群
import numpy as np
import matplotlib.pyplot as plt
from itertools import combinations
import warnings
# 离散化函数(新增)
def discretize_position(pos, discrete_idx=0, discrete_values=[0, 1, 2]):
"""将指定位置的变量离散化"""
# 只处理离散变量位置
discrete_var = pos[:, discrete_idx]
# 将连续值映射到离散值
# 将[0,1)范围分成三等分,分别对应0,1,2
bins = np.linspace(0, 1, len(discrete_values) + 1)
for i in range(len(discrete_values)):
mask = (discrete_var >= bins[i]) & (discrete_var < bins[i+1])
pos[mask, discrete_idx] = discrete_values[i]
# 确保最后一个值也被正确处理
mask = (discrete_var == 1)
pos[mask, discrete_idx] = discrete_values[-1]
return pos
# 设置多目标函数
def multi_obj_func(x):
# 计算第一个目标函数
obj1 = -10 * (np.exp(-0.2 * np.sqrt(x[:, 0]**2 + x[:, 1]**2)) + \
np.exp(-0.2 * np.sqrt(x[:, 1]**2 + x[:, 2]**2)))
# 计算第二个目标函数
obj2 = np.sum(np.abs(x)**0.8 + 5 * np.sin(x**3), axis=1)
# 将两个目标函数的结果按列堆叠
return np.column_stack((obj1, obj2))
# 主函数
def MOPSO(params, MultiObj):
# ... (前面的代码保持不变) ...
Np = params['Np']
Nr = params['Nr']
maxgen = params['maxgen']
W = params['W']
C1 = params['C1']
C2 = params['C2']
ngrid = params['ngrid']
maxvel = params['maxvel']
u_mut = params['u_mut']
fun = MultiObj['fun']
# 表示有几个变量,
nVar = MultiObj['nVar']
# 变量的最小值,
var_min = MultiObj['var_min']
# 变量的最大值
var_max = MultiObj['var_max']
# 初始化粒子的取值,位置代表变量取值
# 200x3
POS = np.random.rand(Np, nVar) * (var_max - var_min) + var_min
# 将第一个变量离散化为0,1,2 (新增)
discrete_idx = 0 # 指定第一个变量(x1)为离散变量
discrete_values = [0, 1, 2] # 离散变量的取值范围
POS = discretize_position(POS, discrete_idx, discrete_values)
VEL = np.zeros((Np, nVar))
# 代表每个粒子的适应度,有两个目标的适应度
# 200x2
POS_fit = fun(POS)
# 第一轮都是最优
# 用于记录每个粒子的最优参数
PBEST = POS.copy()
# 用于记录每个粒子的最优适应度
# 适应度要尽可能的小
PBEST_fit = POS_fit.copy()
# 检查支配关系
# DOMINATED里面=1的点,是要被淘汰的,
DOMINATED = checkDomination(POS_fit)
# 精英库,将最优节点添加进精英库
REP = {}
# 精英库参数添加,~DOMINATED = 1 时候,会被添加进去
REP['pos'] = POS[~DOMINATED, :]
# 最优适应度添加
REP['pos_fit'] = POS_fit[~DOMINATED, :]
# REP['pos'] = POS[np.logical_not(DOMINATED), :]
# REP['pos_fit'] = POS_fit[np.logical_not(DOMINATED), :]
# 更新了网格质量
REP = updateGrid(REP, ngrid)
# 求出最大速度
maxvel = (var_max - var_min) * maxvel / 100
# 代数
#####随机惯性权重
w_min = params.get('w_min', 0.4)
w_max = params.get('w_max', 0.9)
sigma = params.get('sigma', 0.1)
####压缩因子法
c1 = 2.05 # 个体学习因子
c2 = 2.05 # 社会学习因子
C = c1 + c2
# 计算收缩因子
fai = 2.0 / abs(2 - C - np.sqrt(C**2 - 4*C))
gen = 1
# 打印代数,以及精英粒子数
print(f"Generation #0 - Repository size: {REP['pos'].shape[0]}")
stopCondition = False
while not stopCondition:
# ... (前面的代码保持不变) ...
h = selectLeader(REP)
# 更新速度
#####随机惯性权重
w = w_min + (w_max - w_min) * np.random.rand() + sigma * np.random.randn()
VEL = fai*(W * VEL + C1 * np.random.rand(Np, nVar) * (PBEST - POS) + C2 * np.random.rand(Np, nVar) * (np.tile(REP['pos'][h, :], (Np, 1)) - POS))
# 更新位置
POS = POS + VEL
# 将第一个变量离散化为0,1,2 (新增)
POS = discretize_position(POS, discrete_idx, discrete_values)
# 粒子变异
POS = mutation(POS, gen, maxgen, Np, var_max, var_min, nVar, u_mut)
# 将第一个变量离散化为0,1,2 (新增)
POS = discretize_position(POS, discrete_idx, discrete_values)
# 超出边界的,对速度和边界做一个修正
POS, VEL = checkBoundaries(POS, VEL, maxvel, var_max, var_min)
# 将第一个变量离散化为0,1,2 (新增)
POS = discretize_position(POS, discrete_idx, discrete_values)
POS_fit = fun(POS)
# 更新精英库
REP = updateRepository(REP, POS, POS_fit, ngrid)
REP['reduce'] = 0
if REP['pos'].shape[0] > Nr:
# 精英库满了,在比较,删除相对不好的
REP = deleteFromRepository(REP, REP['pos'].shape[0] - Nr, ngrid)
# 返回1说明,说明前面那个点要更优秀
# 也就是说 pos_best 中 1 的参数,是要比PBEST_fit更好的
pos_best = dominates(POS_fit, PBEST_fit)
# dominates返回值中1是可以明确比出好坏的,而0是不可以的
# ~就相当于给1变成0,0变成1,也就是说,best_pos中1是说明比不出来好坏的参数
best_pos = ~dominates(PBEST_fit, POS_fit)
# 那么就让其中接近一半的点都为0,因为比不出来好坏,就部分替换,本轮最优解部分替换之前的最优解
best_pos[np.random.rand(Np) >= 0.5] = False
# pos_best中为1的点是更好的点
if np.sum(pos_best) > 1:
# 先给表现好的点进行更新
PBEST_fit[pos_best, :] = POS_fit[pos_best, :]
PBEST[pos_best, :] = POS[pos_best, :]
if np.sum(best_pos) > 1:
# 给比不出来好坏的点更新
PBEST_fit[best_pos, :] = POS_fit[best_pos, :]
PBEST[best_pos, :] = POS[best_pos, :]
if REP['reduce'] > 0:
# 都是从0开始的
print(f"Generation #{gen} - Repository size: {REP['pos'].shape[0]} - Eliminate size: {REP['eliminate']} - Add size: {REP['add']} - Delete size: {REP['reduce']}")
else:
print(f"Generation #{gen} - Repository size: {REP['pos'].shape[0]} - Eliminate size: {REP['eliminate']} - Add size: {REP['add']} - Delete size: {0}")
gen += 1
if gen > maxgen:
stopCondition = True
# 在迭代循环内添加(gen循环中)
if gen % 10 == 0:
plt.clf()
plt.scatter(REP['pos_fit'][:,0], REP['pos_fit'][:,1], c='blue', alpha=0.5)
plt.title(f'Generation {gen}/{maxgen}')
plt.pause(0.1) # 动态更新
#h_rep = plt.plot(REP['pos_fit'][:, 0], REP['pos_fit'][:, 1], 'ok')
# 在MOPSO函数的最后添加以下代码(在绘图前或绘图后)
# 在MOPSO函数的最后添加以下代码(在绘图前或绘图后)
# 输出决策空间坐标和目标函数值
print("\n========= 最优解的决策变量和目标值 =========")
print(f"找到 {REP['pos'].shape[0]} 个Pareto最优解")
print("------------------------------------------")
print("索引\t x1\t\t x2\t\t x3\t\t f1\t\t f2")
print("------------------------------------------")
for i in range(len(REP['pos'])):
x1, x2, x3 = REP['pos'][i]
f1, f2 = REP['pos_fit'][i]
print(f"{i+1:2d}\t{x1:8.5f}\t{x2:8.5f}\t{x3:8.5f}\t{f1:8.5f}\t{f2:8.5f}")
print("==========================================")
plt.figure(figsize=(10, 6))
plt.scatter(
REP['pos_fit'][:, 0],
REP['pos_fit'][:, 1],
c=np.arange(len(REP['pos_fit'])), # 颜色映射迭代过程
cmap='viridis',
s=40,
edgecolor='k',
alpha=0.7
)
# 添加优化信息标注
plt.title(f'MOPSO Pareto Front (Gen={maxgen}, Particles={params["Np"]})')
plt.xlabel('Objective 1: Solution Quality')
plt.ylabel('Objective 2: Resource Consumption')
plt.grid(alpha=0.3)
plt.colorbar(label='Solution Index')
# 标注最优解
ideal_point = np.min(REP['pos_fit'], axis=0)
plt.scatter(ideal_point[0], ideal_point[1], s=100, marker='*', c='red', label='Ideal Point')
plt.legend()
plt.tight_layout()
plt.savefig('mopso_pareto_front.png', dpi=300)
plt.show()
def updateRepository(REP, POS, POS_fit, ngrid):
# DOMINATED里面=1的点,是要被淘汰的,也就是说1是不好的点
DOMINATED = checkDomination(POS_fit)
# 获取原来精英库的粒子库
# REP['pos'].shape[0]看的这个数组的行数,从1开始
countElite = REP['pos'].shape[0]
countCivilian = POS.shape[0] - sum(DOMINATED)
# 将这些优秀的点添加进入精英库中,axis表示拼接的方向,axis = 0 表示要从行方向拼接
REP['pos'] = np.concatenate((REP['pos'], POS[~DOMINATED, :]), axis=0)
REP['pos_fit'] = np.concatenate((REP['pos_fit'], POS_fit[~DOMINATED, :]), axis=0)
# 在对精英库,进行支配排序
DOMINATED = checkDomination(REP['pos_fit'])
# 求原来库中被淘汰的个数,从0到countElite,但是并不包含countElite,刚好可以给原来的精英库覆盖,因为数组从0开始
REP['eliminate'] = sum(DOMINATED[:countElite])
REP['add'] = countCivilian - sum(DOMINATED[countElite:])
# 用优秀点覆盖原来的点
REP['pos_fit'] = REP['pos_fit'][~DOMINATED, :]
REP['pos'] = REP['pos'][~DOMINATED, :]
# 更新网格质量
REP = updateGrid(REP, ngrid)
# 返回精英库
return REP
def checkBoundaries(POS, VEL, maxvel, var_max, var_min):
# 和malba 中 repmat 类似,功能一样
# np.tile(array, (m, n))
# 相当于array在行方向变为m个
# 相当于array在列方向变成n个
MAXLIM = np.tile(var_max, (POS.shape[0], 1))
MINLIM = np.tile(var_min, (POS.shape[0], 1))
MAXVEL = np.tile(maxvel, (POS.shape[0], 1))
MINVEL = -MAXVEL
# 如果速度过大过小的的,都会拿一个数值限制
VEL[VEL > MAXVEL] = MAXVEL[VEL > MAXVEL]
VEL[VEL < MINVEL] = MINVEL[VEL < MINVEL]
# 碰壁以后,速度变反
VEL[POS > MAXLIM] = -VEL[POS > MAXLIM]
# 修正为边界
POS[POS > MAXLIM] = MAXLIM[POS > MAXLIM]
# 碰壁以后,速度变反
VEL[POS < MINLIM] = -VEL[POS < MINLIM]
# 修正为边界
POS[POS < MINLIM] = MINLIM[POS < MINLIM]
# 返回位置,速度
return POS, VEL
def checkDomination(fitness):
# 粒子个数
Np = fitness.shape[0]
# 用于存放支配关系
dom_vector = np.zeros(Np)
# 排列组合算是
# all_perm = list(combinations(range(1, Np+1), 2))
# matlab从1开始,python从0开始
all_perm = list(combinations(range(0, Np+0), 2))
# 给上下拼接到一起
all_perm = np.concatenate((all_perm, np.flip(all_perm, axis=1)), axis=0)
c = all_perm[:, 0]
# 返回1说明,说明前面那个点要更优秀
d = dominates(fitness[all_perm[:, 0], :], fitness[all_perm[:, 1], :])
# 并不能根据直接的支配关系来找比较好的点,A>B,C>A,这中A就会被淘汰的,所以只能通过d==1找出一定会被淘汰的点
dominated_particles = np.unique(all_perm[d == 1, 1])
# 把要淘汰的点标记为1
dom_vector[dominated_particles] = 1
# 转化为布尔值,不然后边没办法按位取反
dom_vector = dom_vector.astype(bool)
# 返回要淘汰的点
return dom_vector
def dominates(x, y):
# all axis = 1 说明要从行方向来看,1行都是1才返回1
# any axis = 1 说明要从行方向来看,1行有1就返回1
# 这块是要x全部都要小于y,而且x和y还不能说两个维度都相等
# 返回1说明,x这个点要更优秀
result = np.all(x <= y, axis=1) & np.any(x < y, axis=1)
return result
def updateGrid(REP, ngrid):
# 目标适应度个数
ndim = REP['pos_fit'].shape[1]
# 20个网格,21和节点,REP里面的点就是帕利托前沿的点了
REP['hypercube_limits'] = np.zeros((ngrid + 1, ndim))
# 把两个适应度均分ngrid份
for dim in range(ndim):
REP['hypercube_limits'][:, dim] = np.linspace(np.min(REP['pos_fit'][:, dim]), np.max(REP['pos_fit'][:, dim]), ngrid + 1)
# 查看精英库里面的节点个数,0代表行数,1代表列数
npar = REP['pos_fit'].shape[0]
# 记录索引,将下标转换为矩阵的线性索引,
REP['grid_idx'] = np.zeros(npar, dtype=int) # 先行后列
# 网格位置
REP['grid_subidx'] = np.zeros((npar, ndim), dtype=int)
for n in range(npar):
idnames = ""
# 这块算是计算了两个方向的拥挤度了
for d in range(ndim):
# 这是找这个适应度在第几格,这个相比于matlab代码去除了减一,因为python从0开始的
REP['grid_subidx'][n, d] = np.where(REP['pos_fit'][n, d] <= REP['hypercube_limits'][:, d])[0][0]
# 这块是有一个边缘处理的
if REP['grid_subidx'][n, d] == -1:
REP['grid_subidx'][n, d] = 0
# 这个就不用了
# idnames += "," + str(REP['grid_subidx'][n, d])
# REP['grid_idx'][n] = eval(f"np.ravel_multi_index([{idnames[1:]}], [ngrid] * ndim)")
row = REP['grid_subidx'][n, 0]
col = REP['grid_subidx'][n, 1]
if ndim == 2:
array_shape = (ngrid,ngrid)
if ndim == 3:
array_shape = (ngrid,ngrid,ngrid)
# 获得索引位置
REP['grid_idx'][n] = sub2ind(array_shape,row,col)
# 网格质量这块,20不够的,原来的代码可能是只考虑一个维度的网格,后来考虑;两个维度的网格,可能忘记改了
REP['quality'] = np.zeros((ngrid*ngrid, 2))
# 去除重复的,而且还会唯一元素出现的个数,
ids, counts = np.unique(REP['grid_idx'], return_counts=True)
for i in range(len(ids)):
REP['quality'][i, 0] = ids[i]
# 这个是用来统计同一个网格出现的次数,这个可以用其他来替代,
# REP['quality'][i, 1] = 10 / np.sum(REP['grid_idx'] == ids[i])
# 这是我自己修改的
REP['quality'][i, 1] = 10 / counts[i]
return REP
def selectLeader(REP):
# 按概率走的,都能选到,只是说,点少的,更容易选中,有点轮盘赌的味道
prob = np.cumsum(REP['quality'][:, 1])
# 按概率选一个网格
sel_hyp = REP['quality'][np.where(np.random.rand() * np.max(prob) <= prob)[0][0], 0]
# idx是点的顺序
idx = np.arange(len(REP['grid_idx']))
# 把这个网格里面的点选出来
selected = idx[REP['grid_idx'] == sel_hyp]
# 再从选出来的点中,随机取一个
selected = selected[np.random.randint(len(selected))]
# 返回选的点
return selected
def deleteFromRepository(REP, n_extra, ngrid):
REP['reduce'] = n_extra
# 先确定有多少个点
crowding = np.zeros(REP['pos'].shape[0])
for m in range(REP['pos_fit'].shape[1]):
# 对适应度排序,排序是为了算距离
m_fit = REP['pos_fit'][:, m]
# id记录的是原来的位置
idx = np.argsort(m_fit)
# 排序完的,1,2,3,4,这种是对应的距离
m_fit_sorted = m_fit[idx]
# 计算点和相邻两个点的距离,np.inf表示无限大
m_up = np.concatenate((m_fit_sorted[1:], [np.inf]))
m_down = np.concatenate(([np.inf], m_fit_sorted[:-1]))
distance = (m_up - m_down) / (max(m_fit_sorted) - min(m_fit_sorted))
# 再把顺序换回去,idx_back就是每个粒子距离再distance中的位置
idx_back = np.argsort(idx)
# 因为 inf - inf 会变成 NAN 会报错,所以要忽略这个,后边会对这个进行处理
# 忽略 'invalid value encountered in add' 类型的 RuntimeWarning
warnings.filterwarnings('ignore', category=RuntimeWarning, message="invalid value encountered in add")
crowding = crowding + distance[idx_back]
# 恢复 RuntimeWarning
warnings.resetwarnings()
# 给nan变成inf,方便排序
crowding[np.isnan(crowding)] = np.inf
# del_idx = np.argsort(crowding)
# del_idx = del_idx[:n_extra]
# 排序,选出距离最小的点
del_idx = np.argsort(crowding)[:n_extra]
# axis = 0 表示沿行进行,np.delete 是 NumPy 库中的一个函数,用于删除数组中指定的元素。
REP['pos'] = np.delete(REP['pos'], del_idx, axis=0)
REP['pos_fit'] = np.delete(REP['pos_fit'], del_idx, axis=0)
# 更新网格
REP = updateGrid(REP, ngrid)
return REP
# 修改变异函数以处理离散变量
def mutation(POS, gen, maxgen, Np, var_max, var_min, nVar, u_mut):
# 给种群数分三份,np.floor 用于取整
fract = Np / 3 - np.floor(Np / 3)
if fract < 0.5:
# np.round 四舍五入 np.ceil向上取整
sub_sizes = [np.ceil(Np / 3), np.round(Np / 3), np.round(Np / 3)]
else:
sub_sizes = [np.round(Np / 3), np.round(Np / 3), np.floor(Np / 3)]
# 用来确定粒子
cum_sizes = np.cumsum(sub_sizes)
# 第二个种群全部变异
nmut = np.round(u_mut * sub_sizes[1])
if nmut > 0:
# 按概率抽选出要变异的粒子,replace=false表示是不放回抽样
idx = cum_sizes[0] + np.random.choice(np.arange(sub_sizes[1]), size=int(nmut), replace=False)
# 给取整,map可以对数组批量处理,list转换结果
idx = list(map(int, idx))
# 对位置进行随机
new_pos = np.random.rand(int(nmut), nVar) * (var_max - var_min) + var_min
# 保留第一个离散变量不变(新增)
new_pos[:, 0] = POS[idx, 0] # 保持离散变量不变
POS[idx, :] = new_pos
# 第三个种群部分变异,**是指数
per_mut = (1 - gen / maxgen) ** (5 * nVar)
nmut = np.round(per_mut * sub_sizes[2])
if nmut > 0:
idx = cum_sizes[1] + np.random.choice(np.arange(sub_sizes[2]), size=int(nmut), replace=False)
# 给取整,map可以对数组批量处理,list转换结果
idx = list(map(int, idx))
# 对位置进行随机
new_pos = np.random.rand(int(nmut), nVar) * (var_max - var_min) + var_min
# 保留第一个离散变量不变(新增)
new_pos[:, 0] = POS[idx, 0] # 保持离散变量不变
POS[idx, :] = new_pos
# 返回位置
return POS
def sub2ind(shape, row, col):
# 将行索引和列索引转换为线性索引
return row * shape[1] + col
# ... (其他函数保持不变) ...
# 设置参数
params = {
# 粒子数
'Np': 500,
# 精英库
'Nr': 1000,
'maxgen': 200,
'W': 0.4,
'C1': 2,
'C2': 2,
# 网格个数
'ngrid': 20,
'maxvel': 5,
'u_mut': 0.5
}
# 设置多目标函数
MultiObj = {
'fun': multi_obj_func,
'nVar': 3,
'var_min': np.array([0, -5, -5]), # x1最小值设为0(离散变量)
'var_max': np.array([2, 5, 5]) # x1最大值设为2(离散变量)
}
REP = MOPSO(params, MultiObj)
python
##NASA-II
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import math as mt
from matplotlib.colors import LinearSegmentedColormap
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
# 目标函数定义
def funclsin(x):
return (x - 1)**2 # 目标函数1:离中心点(1)的距离平方
def funclcos(x):
return mt.cos(x) # 目标函数2:余弦函数(模拟阳光照射)
# 遗传算法参数设置
pi = mt.pi
NP = 70 # 种群大小
L = 10 # 染色体长度(二进制编码)
Pc = 0.8 # 交叉概率
Pm = 0.2 # 变异概率
G = 20 # 迭代次数
Xs = pi/2 # 解空间上限
Xx = 0 # 解空间下限
# 初始化种群
f = np.random.randint(0, high=2, size=(NP, L))
x = np.zeros(NP)
f1vals = np.zeros(NP) # 存储目标函数1的值
f2vals = np.zeros(NP) # 存储目标函数2的值
# 绘图设置
plt.figure(figsize=(15, 10))
plt.style.use('ggplot')
# 存储每代最优解
best_solutions = []
all_generations = [] # 存储每代种群信息
# 自定义颜色映射(从蓝色到红色)
colors = LinearSegmentedColormap.from_list('custom', ['#1f77b4', '#ff7f0e'])
#%% 遗传算法主循环
for i in range(G):
print(f"第 {i+1}/{G} 代")
nf = f.copy() # 新的种群
# 交叉操作
for M in range(0, NP, 2):
if np.random.rand() < Pc:
q = np.random.randint(0, 2, L) # 随机交叉位
for j in range(L):
if q[j] == 1:
nf[M, j], nf[M+1, j] = nf[M+1, j], nf[M, j]
# 变异操作
mutation_count = 0
while mutation_count < NP * Pm:
h = np.random.randint(0, NP) # 随机选择个体
g = np.random.randint(0, L) # 随机选择基因位
nf[h, g] = 1 - nf[h, g] # 二进制取反
mutation_count += 1
# 合并父代和子代
newf = np.vstack((f, nf))
# 解码染色体并计算目标函数值
f1 = []
f2 = []
decoded_x = []
for j in range(newf.shape[0]):
U = newf[j]
m = 0
for k in range(L):
m = U[k] * (2**(L-1-k)) + m # 修正解码公式
x_val = Xx + m * (Xs - Xx) / (2**L - 1) # 修正解码公式
decoded_x.append(x_val)
f1.append(funclsin(x_val))
f2.append(funclcos(x_val))
# 构建目标函数矩阵
fs = np.array([f1, f2]).T
# 非支配排序
ps = np.zeros((len(f1), len(f1)))
for k in range(len(f1)):
for j in range(len(f1)):
if k != j: # 不与自己比较
if fs[k, 0] <= fs[j, 0] and fs[k, 1] <= fs[j, 1]:
if fs[k, 0] < fs[j, 0] or fs[k, 1] < fs[j, 1]:
ps[k, j] = 1 # k支配j
# 计算被支配次数
jishu = np.sum(ps, axis=0)
# 分层排序
sortjishu = np.sort(jishu)
index = np.argsort(jishu)
aaa = np.unique(sortjishu)
front = []
for k in range(len(aaa)):
front_layer = []
for j in range(len(index)):
if jishu[index[j]] == aaa[k]:
front_layer.append(index[j])
front.append(front_layer)
# 拥挤距离计算
selected = []
for layer_idx, layer in enumerate(front):
if len(selected) + len(layer) <= NP:
# 整层加入
selected.extend(layer)
else:
# 需要从当前层选择部分个体
tempf = [newf[i] for i in layer]
tempf1 = [fs[i, 0] for i in layer]
tempf2 = [fs[i, 1] for i in layer]
# 拥挤距离初始化
distance = np.zeros(len(tempf1))
# 按f1排序计算拥挤距离
f1_idx = np.argsort(tempf1)
distance[f1_idx[0]] = np.inf # 边界点
distance[f1_idx[-1]] = np.inf
for k in range(1, len(f1_idx)-1):
if tempf1[f1_idx[-1]] != tempf1[f1_idx[0]]: # 避免除零
distance[f1_idx[k]] += (tempf1[f1_idx[k+1]] - tempf1[f1_idx[k-1]]) / (tempf1[f1_idx[-1]] - tempf1[f1_idx[0]])
# 按f2排序计算拥挤距离
f2_idx = np.argsort(tempf2)
distance[f2_idx[0]] = np.inf # 边界点
distance[f2_idx[-1]] = np.inf
for k in range(1, len(f2_idx)-1):
if tempf2[f2_idx[-1]] != tempf2[f2_idx[0]]: # 避免除零
distance[f2_idx[k]] += (tempf2[f2_idx[k+1]] - tempf2[f2_idx[k-1]]) / (tempf2[f2_idx[-1]] - tempf2[f2_idx[0]])
# 按拥挤距离降序选择
dis_index = np.argsort(distance)[::-1]
remaining = NP - len(selected)
for idx in dis_index[:remaining]:
selected.append(layer[idx])
break
# 更新种群
f = newf[selected[:NP]]
# 解码当前代的最优解
for j in range(NP):
U = f[j]
m = 0
for k in range(L):
m = U[k] * (2**(L-1-k)) + m
x[j] = Xx + m * (Xs - Xx) / (2**L - 1)
f1vals[j] = funclsin(x[j])
f2vals[j] = funclcos(x[j])
# 存储当前代信息
all_generations.append({
'generation': i+1,
'solutions': x.copy(),
'f1': f1vals.copy(),
'f2': f2vals.copy(),
'population': f.copy()
})
# 存储当前代的最优解(第一层非支配解)
current_best = []
for idx in front[0]:
if idx < len(decoded_x): # 确保索引有效
current_best.append({
'x': decoded_x[idx],
'f1': fs[idx, 0],
'f2': fs[idx, 1],
'generation': i+1
})
best_solutions.append(current_best)
#%% 结果可视化
# 1. 所有解的分布图
plt.figure(figsize=(12, 8))
for i, gen in enumerate(all_generations):
color_intensity = i / G # 根据代数确定颜色深浅
plt.scatter(gen['f1'], gen['f2'], color=colors(color_intensity),
alpha=0.3, label=f'Gen {i+1}' if i % 5 == 0 else "")
# 添加Pareto前沿(最后一层)
last_gen = all_generations[-1]
plt.scatter(last_gen['f1'], last_gen['f2'], color='red', s=80,
edgecolor='black', label='Pareto Front (Final Gen)')
plt.title('Multi-Objective Optimization: Solution Distribution')
plt.xlabel('Objective 1: Distance to Center $(x-1)^2$')
plt.ylabel('Objective 2: Sun Exposure $cos(x)$')
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
plt.tight_layout()
plt.savefig('solution_distribution.png', dpi=300)
plt.show()
# 2. Pareto前沿展示
plt.figure(figsize=(12, 8))
# 收集所有代的最优解
all_best_f1 = []
all_best_f2 = []
for gen in best_solutions:
for sol in gen:
all_best_f1.append(sol['f1'])
all_best_f2.append(sol['f2'])
# 绘制所有代的最优解
plt.scatter(all_best_f1, all_best_f2, c=range(len(all_best_f1)),
cmap='viridis', alpha=0.6, label='All Generations Pareto Solutions')
# 绘制最终代的最优解
final_f1 = [sol['f1'] for sol in best_solutions[-1]]
final_f2 = [sol['f2'] for sol in best_solutions[-1]]
plt.scatter(final_f1, final_f2, color='red', s=100,
edgecolor='black', zorder=10, label='Final Generation Pareto Front')
# 添加Pareto前沿的凸包
sorted_idx = np.argsort(final_f1)
sorted_f1 = np.array(final_f1)[sorted_idx]
sorted_f2 = np.array(final_f2)[sorted_idx]
plt.plot(sorted_f1, sorted_f2, 'r--', linewidth=2, alpha=0.7)
plt.title('Evolution of Pareto Front')
plt.xlabel('Objective 1: Distance to Center $(x-1)^2$')
plt.ylabel('Objective 2: Sun Exposure $cos(x)$')
plt.colorbar(label='Solution Index')
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
plt.tight_layout()
plt.savefig('pareto_front.png', dpi=300)
plt.show()
# 3. 最优解的变量值分布
plt.figure(figsize=(12, 8))
# 收集所有最优解的x值
all_best_x = []
for gen in best_solutions:
for sol in gen:
all_best_x.append(sol['x'])
# 绘制直方图
plt.hist(all_best_x, bins=20, color='#2ca02c', edgecolor='black', alpha=0.7)
plt.axvline(np.mean(all_best_x), color='red', linestyle='dashed', linewidth=2,
label=f'Mean: {np.mean(all_best_x):.3f}')
plt.title('Distribution of Optimal Solutions (x-values)')
plt.xlabel('Solution Position (x)')
plt.ylabel('Frequency')
plt.grid(axis='y', alpha=0.75)
plt.legend()
plt.tight_layout()
plt.savefig('solution_histogram.png', dpi=300)
plt.show()
# 4. 动画展示进化过程
fig, ax = plt.subplots(figsize=(10, 8))
ax.set_xlim(0, max(all_best_f1)+0.1)
ax.set_ylim(min(all_best_f2)-0.1, 1.1)
ax.set_xlabel('Objective 1: Distance to Center $(x-1)^2$')
ax.set_ylabel('Objective 2: Sun Exposure $cos(x)$')
ax.set_title('Evolution of Solutions')
scat = ax.scatter([], [], c=[], cmap='viridis', alpha=0.7)
gen_text = ax.text(0.02, 0.95, '', transform=ax.transAxes, fontsize=12)
paretos = []
def init():
scat.set_offsets(np.empty((0, 2)))
return scat, gen_text
def update(frame):
gen = all_generations[frame]
points = np.column_stack((gen['f1'], gen['f2']))
# 更新散点图
scat.set_offsets(points)
scat.set_array(np.linspace(0, 1, len(points)))
# 更新文本
gen_text.set_text(f'Generation: {frame+1}/{G}')
# 绘制当前代的Pareto前沿
for p in paretos:
p.remove()
paretos.clear()
current_pareto = np.column_stack(([sol['f1'] for sol in best_solutions[frame]],
[sol['f2'] for sol in best_solutions[frame]]))
sorted_idx = np.argsort(current_pareto[:, 0])
sorted_pareto = current_pareto[sorted_idx]
# 添加Pareto前沿
pareto_line, = ax.plot(sorted_pareto[:, 0], sorted_pareto[:, 1], 'r--', alpha=0.7)
pareto_scatter = ax.scatter(sorted_pareto[:, 0], sorted_pareto[:, 1],
color='red', s=50, edgecolor='black', zorder=10)
paretos.extend([pareto_line, pareto_scatter])
return scat, gen_text, *paretos
ani = FuncAnimation(fig, update, frames=G, init_func=init, blit=True, interval=500)
plt.close(fig)
# 保存动画(可选)
# ani.save('evolution_animation.gif', writer='pillow', fps=2)
# 显示动画
HTML(ani.to_jshtml())
#%% 输出最优解信息
print("\n" + "="*50)
print("最佳解统计信息 (最终代)")
print("="*50)
# 找到最终代Pareto前沿的解
final_pareto = best_solutions[-1]
# 按目标函数1排序
sorted_by_f1 = sorted(final_pareto, key=lambda x: x['f1'])
# 按目标函数2排序
sorted_by_f2 = sorted(final_pareto, key=lambda x: x['f2'])
print(f"\nPareto前沿解数量: {len(final_pareto)}")
print(f"目标函数1范围: {min([s['f1'] for s in final_pareto]):.4f} - {max([s['f1'] for s in final_pareto]):.4f}")
print(f"目标函数2范围: {min([s['f2'] for s in final_pareto]):.4f} - {max([s['f2'] for s in final_pareto]):.4f}")
print("\n最接近中心的解决方案:")
print(f"位置 x = {sorted_by_f1[0]['x']:.4f}")
print(f"目标1: {sorted_by_f1[0]['f1']:.4f}, 目标2: {sorted_by_f1[0]['f2']:.4f}")
print("\n阳光最充足的解决方案:")
print(f"位置 x = {sorted_by_f2[0]['x']:.4f}")
print(f"目标1: {sorted_by_f2[0]['f1']:.4f}, 目标2: {sorted_by_f2[0]['f2']:.4f}")
# 找到平衡解(距离原点最近)
balanced_solution = min(final_pareto, key=lambda x: np.sqrt(x['f1']**2 + x['f2']**2))
print("\n最佳平衡解决方案:")
print(f"位置 x = {balanced_solution['x']:.4f}")
print(f"目标1: {balanced_solution['f1']:.4f}, 目标2: {balanced_solution['f2']:.4f}")
# 输出所有Pareto解
print("\n所有Pareto前沿解:")
print("Index | Position (x) | Objective 1 | Objective 2")
print("-"*45)
for i, sol in enumerate(final_pareto):
print(f"{i+1:5d} | {sol['x']:11.6f} | {sol['f1']:11.6f} | {sol['f2']:11.6f}")