glb模型横倒的一种程序化解决方式

背景

有些模型，在A软件查看时是正常的立着，朝向正常；导出后用B软件打开，可能会遇到模型横倒的情况，导致看着比较难受

比如用Mayo打开一个stp文件，是正常立着的

导出为glb后，用blender打开

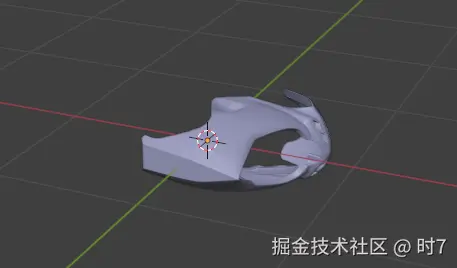
模型是横倒的

‍

这是由于gltf/GLB标准定义了+Y（Y 轴）作为"向上"（Up）方向，右手坐标系

glTF™ 2.0 Specification

默认glb导出是Y轴向上

加载进Z轴向上的坐标系（Blender、CATIA、adsMax、Babylon.js等），就会横倒着，因为它的向上轴是Y轴

‍

下面提供一种程序化的处理方式，方便批量处理这种情况

python脚本处理

用 Python + pygltflib 或 gltf-transform 给 root node 加个旋转：

python 复制代码

from pygltflib import GLTF2
import numpy as np

glb_path = "input.glb"
out_path = "output_zup.glb"

glb = GLTF2().load(glb_path)

# 四元数旋转（绕X轴-90度）
rotation = [ -0.7071068, 0, 0, 0.7071068 ]

# 给第一个节点加旋转
glb.nodes[0].rotation = rotation

glb.save(out_path)

这样任何 Y-up 的 GLB 都能转成 Z-up

‍

同理，Z-up转成Y-up的GLB

改一下旋转就行

python 复制代码

# 四元数旋转：绕 X 轴 +90 度，把 Z-up 转成 Y-up
rotation = [0.7071068, 0, 0, 0.7071068]

‍

原理分析

为什么是 0.7071068，这个数字代表什么？

1. 为什么要绕 X 轴旋转 −90°？

glTF 规范规定：
- Y 轴是 up（向上）
- Z 轴是 forward（朝前）
很多建模工具（Blender、CATIA、3dsMax 等）内部用 Z 轴 up。

所以，当你从 Blender 等导出到 glTF 时，如果想保持"Z 向上"，就需要在 glTF 的根节点加个变换，把 Y-up 系统旋转成 Z-up 系统。

这个旋转就是：

👉 绕 X 轴 −90° （相当于把 glTF 的 Y 向上翻转成 Z 向上）。

‍

2. 四元数是怎么写出来的？

四元数 <math xmlns="http://www.w3.org/1998/Math/MathML"> [ x , y , z , w ] [x, y, z, w] </math>[x,y,z,w] 对应的旋转公式是：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> q = [ sin ⁡ ( θ 2 ) ⋅ v ^ , cos ⁡ ( θ 2 ) ] q = [ \sin(\tfrac{\theta}{2}) \cdot \hat{v}, \cos(\tfrac{\theta}{2}) ] </math>q=[sin(2θ)⋅v^,cos(2θ)]

其中：

<math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ = 旋转角度
<math xmlns="http://www.w3.org/1998/Math/MathML"> v ^ \hat{v} </math>v^ = 单位旋转轴 (x, y, z)

‍

套入当前的情况：

旋转轴：X 轴 → (1, 0, 0)
旋转角度：θ = −90° = −π/2

计算：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> sin ⁡ ( − π 4 ) = − 2 2 ≈ − 0.7071 \sin(\tfrac{-\pi}{4}) = -\tfrac{\sqrt{2}}{2} \approx -0.7071 </math>sin(4−π)=−22 ≈−0.7071
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> cos ⁡ ( − π 4 ) = 2 2 ≈ 0.7071 \cos(\tfrac{-\pi}{4}) = \tfrac{\sqrt{2}}{2} \approx 0.7071 </math>cos(4−π)=22 ≈0.7071

得到：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> q = [ − 0.7071 , 0 , 0 , 0.7071 ] q = [ -0.7071, 0, 0, 0.7071 ] </math>q=[−0.7071,0,0,0.7071]

就是你写的 [ -0.7071068, 0, 0, 0.7071068 ]。

‍

3. 为什么加在 `nodes[0].rotation` 上？

在 glTF/GLB 文件中，场景的几何都挂在 根节点（node 0） 或其子节点上。
给 nodes[0] 加一个旋转，等于对整个模型施加了一个全局坐标系变换。
这样就不需要逐个 mesh 去旋转了。

‍

Z-up → Y-up

旋转思路：

之前 Y-up → Z-up 用的是 绕 X 轴 −90° ；
现在要反过来，所以是 绕 X 轴 +90° 。

四元数计算

四元数公式：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> q = [ sin ⁡ ( θ 2 ) ⋅ x , sin ⁡ ( θ 2 ) ⋅ y , sin ⁡ ( θ 2 ) ⋅ z , cos ⁡ ( θ 2 ) ] q = [\sin(\tfrac{\theta}{2}) \cdot x, \sin(\tfrac{\theta}{2}) \cdot y, \sin(\tfrac{\theta}{2}) \cdot z, \cos(\tfrac{\theta}{2})] </math>q=[sin(2θ)⋅x,sin(2θ)⋅y,sin(2θ)⋅z,cos(2θ)]

取：

旋转轴 = X 轴 = (1,0,0)
角度 θ = +90° = +π/2

计算：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> sin ⁡ ( π / 4 ) = + 0.7071 , cos ⁡ ( π / 4 ) = 0.7071 \sin(π/4) = +0.7071,\ \cos(π/4) = 0.7071 </math>sin(π/4)=+0.7071, cos(π/4)=0.7071

所以：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> q = [ 0.7071 , 0 , 0 , 0.7071 ] q = [0.7071, 0, 0, 0.7071] </math>q=[0.7071,0,0,0.7071]

‍

如果还有其他比较好的方式，欢迎留言分享

‍

glb模型横倒的一种程序化解决方式