这是一个水星热演化核幔耦合数值模拟系统,主要功能如下:
核心功能
模拟水星45亿年的热演化历史,特别是核幔边界的凝固过程和温度场演化。
物理模型特点
1. 两种凝固模式
-
• AS系列(向外凝固):从核中心向外凝固
-
• BS系列(向内凝固):从核幔边界向内凝固
2. 完整的物理过程
-
• 热传导:在固态区求解热传导方程
-
• 相变过程:考虑凝固/熔化相变
-
• 对流效应:通过瑞利数和努塞尔数描述
-
• 能量守恒:跟踪总能量变化
-
• 引力势能:在高级模型中包含引力能释放
数值方法
关键技术
-
• 有限差分法:空间离散化
-
• 稀疏矩阵求解 :使用
scipy.sparse.linalg.spsolve高效求解 -
• 自适应时间步长:自动检测并调整不稳定步长
-
• 数值稳定性保护:限制指数函数、避免除零错误
稳定性增强
# 示例保护措施
exponent = min(self.nu_param * (R**2 - r**2), 100) # 限制指数大小
value = max(min(value, upper_bound), lower_bound) # 数值范围限制输出结果
主要监测参数
-
• ICB(内核边界)半径演化
-
• 中心温度、CMB(核幔边界)温度
-
• 瑞利数、努塞尔数(对流强度)
-
• CMB热流
-
• 能量守恒误差
可视化功能
-
• 多标签页交互图表
-
• 温度剖面随时间演化
-
• 参数对比分析
系统特色
用户友好界面
-
• Streamlit Web应用:图形化操作界面
-
• 并行计算支持:多模型同时运行
-
• 实时进度显示:计算过程可视化
-
• 结果导出:HDF5格式数据保存
工程优化
-
• 健壮性:异常处理和备用算法
-
• 效率:稀疏矩阵和并行计算
-
• 可扩展性:模块化设计便于扩展
代码
import numpy as np
import streamlit as st
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from scipy.sparse import diags
from scipy.sparse.linalg import spsolve
import pandas as pd
import time
import sys
import os
from concurrent.futures import ThreadPoolExecutor
import h5py
from datetime import datetime
from scipy.integrate import trapezoid
class MercuryThermalModel:
"""水星热演化核幔耦合数值模型 - 优化版本"""
def __init__(self, model_type='AS1', mesh_size=500, time_step=0.237):
self.model_type = model_type
self.mesh_size = mesh_size
self.original_dt = time_step * 1e6 * 365.25 * 24 * 3600
self.dt = self.original_dt # 当前时间步长
# 初始化参数
self._initialize_physical_parameters()
self._set_model_parameters()
self._initialize_grid()
self._initialize_temperature()
# 结果存储
self.results = {
'time': [], 'icb_radius': [], 't_center': [], 't_icb': [],
't_cmb': [], 'ra_mantle': [], 'nu_mantle': [], 'q_cmb': [],
'solidification_rate': [], 'energy_balance': [], 'temperature_profiles': [],
'time_steps': [] # 记录实际使用的时间步长
}
# 稳定性控制标志
self.dt_stability_warned = False # 避免重复警告
self.dt_adjustment_count = 0 # 时间步长调整次数
self.max_dt_adjustments = 10 # 最大调整次数
def _initialize_physical_parameters(self):
"""初始化物理参数"""
# 水星基本参数
self.R_mercury = 2440e3
self.R_core = 1900e3
# 核物性参数
self.rho_c = 8380
self.Delta_rho = 400
self.gamma = 1.4
self.K = 3.3e11
# 热物理参数
self.k_m = 2.7
self.rho_m = 3060
self.cp_m = 1297
self.alpha_m = 3e-5
# 核热物理参数
if self.model_type.startswith('AS'):
self.alpha_c = 2e-5
self.cp_c = 750
else:
self.alpha_c = 5e-5
self.cp_c = 465
self.k_s = 100
self.L = 600e3
# 初始条件
self.T0 = 445
self.TL_b = 2000
# 常数
self.G = 6.67430e-11
# 计算参数 - 添加数值稳定性保护
self.lambda_param = min((4 * np.pi * self.G * self.rho_c ** 2 *
(self.gamma - 1 / 3)) / (3 * self.K), 1e-10)
self.nu_param = min((2 * np.pi * self.G * self.alpha_c * self.rho_c) / (3 * self.cp_c), 1e-10)
self.TL_0 = min(self.TL_b * np.exp(self.lambda_param * self.R_core ** 2), 10000)
# 热扩散率
self.kappa_m = self.k_m / (self.rho_m * self.cp_m)
self.kappa_s = self.k_s / (self.rho_c * self.cp_c)
def _set_model_parameters(self):
"""设置模型参数"""
if self.model_type.startswith('AS'):
self.solidification_mode = 'outward'
self.include_radioheat = self.model_type != 'AS1'
self.include_gravitational = self.model_type == 'AS3'
self.R_icb = 0.1 * self.R_core
else:
self.solidification_mode = 'inward'
self.include_radioheat = self.model_type != 'BS1'
self.include_gravitational = self.model_type == 'BS3'
self.R_icb = 0.9 * self.R_core
def _initialize_grid(self):
"""初始化计算网格"""
# 避免网格点过密导致的数值问题
self.mesh_size = min(self.mesh_size, 1000)
self.mesh_size = max(self.mesh_size, 100)
self.r_mantle = np.linspace(self.R_core, self.R_mercury, self.mesh_size)
self.dr_mantle = self.r_mantle[1] - self.r_mantle[0]
self.r_core = np.linspace(1e-10, self.R_core, self.mesh_size) # 避免r=0的奇点
self.dr_core = self.r_core[1] - self.r_core[0]
self.t_max = 4.5e9 * 365.25 * 24 * 3600
def _initialize_temperature(self):
"""初始化温度场"""
self.T_mantle = np.linspace(self.TL_b, self.T0, self.mesh_size)
self.T_core = self._initialize_core_temperature()
def _initialize_core_temperature(self):
"""初始化核温度场 - 添加数值稳定性"""
T_core = np.zeros(self.mesh_size)
if self.solidification_mode == 'outward':
for i, r in enumerate(self.r_core):
if r <= self.R_icb:
T_core[i] = self.TL_0 + (self.TL_b - self.TL_0) * (r / max(self.R_icb, 1e-10))
else:
# 限制指数大小避免溢出
exponent = min(self.nu_param * (self.R_icb ** 2 - r ** 2), 100)
T_core[i] = self.TL_b * np.exp(exponent)
else:
for i, r in enumerate(self.r_core):
if r < self.R_icb:
exponent = min(self.nu_param * (self.R_core ** 2 - r ** 2), 100)
T_core[i] = self.TL_b * np.exp(exponent)
else:
denominator = max(self.R_core - self.R_icb, 1e-10)
T_core[i] = self.TL_b + (self.T0 - self.TL_b) * ((r - self.R_icb) / denominator)
return np.clip(T_core, 100, 10000) # 限制温度在合理范围内
def _check_time_step_stability(self, dt):
"""检查时间步长稳定性,避免重复警告"""
alpha = self.kappa_m * dt / self.dr_mantle ** 2
if alpha > 0.5:
dt_stable = 0.5 * self.dr_mantle ** 2 / self.kappa_m
if not self.dt_stability_warned:
st.warning(f"时间步长不稳定,自动调整为 {dt_stable:.2e} 秒")
self.dt_stability_warned = True
return min(dt, dt_stable * 0.9) # 使用90%的稳定步长
return dt
def _solve_mantle_heat_conduction(self, dt):
"""使用稀疏矩阵求解幔热传导方程 - 增强稳定性"""
# 检查并自动调整时间步长
adjusted_dt = self._check_time_step_stability(dt)
if adjusted_dt != dt:
self.dt = adjusted_dt
dt = adjusted_dt
self.dt_adjustment_count += 1
n = len(self.T_mantle)
r = self.r_mantle
# 稳定性检查
alpha = self.kappa_m * dt / self.dr_mantle ** 2
# 构建三对角矩阵
main_diag = np.ones(n)
lower_diag = np.zeros(n - 1)
upper_diag = np.zeros(n - 1)
for i in range(1, n - 1):
main_diag[i] = 1 + 2 * alpha
lower_diag[i - 1] = -alpha * (1 - self.dr_mantle / (2 * max(r[i], 1e-10)))
upper_diag[i - 1] = -alpha * (1 + self.dr_mantle / (2 * max(r[i], 1e-10)))
# 边界条件
main_diag[0] = 1
main_diag[-1] = 1
lower_diag[0] = 0
upper_diag[-1] = 0
# 构建稀疏矩阵
A = diags([lower_diag, main_diag, upper_diag], [-1, 0, 1], format='csr')
b = self.T_mantle.copy()
b[0] = self.T_core[-1] # CMB温度连续
b[-1] = self.T0 # 表面固定温度
try:
T_new = spsolve(A, b)
return np.clip(T_new, 100, 10000) # 限制温度范围
except:
# 备用求解方法
return np.clip(np.linalg.solve(A.toarray(), b), 100, 10000)
def _calculate_energy_balance(self):
"""计算能量平衡 - 使用更稳定的积分方法"""
try:
# 核热能 - 使用scipy的trapezoid替代np.trapz
integrand_core = self.rho_c * self.cp_c * self.T_core * self.r_core ** 2
integrand_core = np.nan_to_num(integrand_core, nan=0.0, posinf=1e20, neginf=-1e20)
core_energy = 4 * np.pi * trapezoid(integrand_core, self.r_core)
# 幔热能
integrand_mantle = self.rho_m * self.cp_m * self.T_mantle * self.r_mantle ** 2
integrand_mantle = np.nan_to_num(integrand_mantle, nan=0.0, posinf=1e20, neginf=-1e20)
mantle_energy = 4 * np.pi * trapezoid(integrand_mantle, self.r_mantle)
# 相变潜热
latent_energy = (4 / 3) * np.pi * self.R_icb ** 3 * self.rho_c * self.L
total_energy = core_energy + mantle_energy + latent_energy
return max(total_energy, 1e10) # 避免负值
except Exception as e:
return 1e20 # 返回一个安全的大数
def _calculate_phase_boundary_velocity_outward(self, dt):
"""计算向外凝固的相变边界速度 - 增强数值稳定性"""
try:
idx = np.argmin(np.abs(self.r_core - self.R_icb))
# 固态侧热流
if idx > 0:
q_solid = -self.k_s * (self.T_core[idx] - self.T_core[idx - 1]) / max(self.dr_core, 1e-10)
else:
q_solid = 0
# 液态侧热流 - 限制指数大小
exponent = min(self.nu_param * (self.R_icb ** 2 - self.R_icb ** 2), 100)
T_liquid = self.TL_b * np.exp(exponent)
q_liquid = -self.k_s * self.nu_param * 2 * self.R_icb * T_liquid
# 引力势能项
q_G = 0
if self.include_gravitational:
q_G_term = min((2 / 15) * np.pi * self.G * self.rho_c * self.Delta_rho * self.R_icb ** 2, 1e20)
q_G = q_G_term
q_L = self.rho_c * self.L
dc_dt = (q_liquid - q_solid + q_G) / max(q_L, 1e-10)
return np.clip(dc_dt, -1e-10, 1e-10) # 限制速度范围
except Exception as e:
return 0.0
def _calculate_phase_boundary_velocity_inward(self, dt):
"""计算向内凝固的相变边界速度 - 增强数值稳定性"""
try:
idx = np.argmin(np.abs(self.r_core - self.R_icb))
# 限制指数大小
exponent = min(self.nu_param * (self.R_core ** 2 - self.R_icb ** 2), 100)
T_liquid = self.TL_b * np.exp(exponent)
q_liquid = -self.k_s * self.nu_param * 2 * self.R_icb * T_liquid
if idx < len(self.r_core) - 1:
q_solid = -self.k_s * (self.T_core[idx + 1] - self.T_core[idx]) / max(self.dr_core, 1e-10)
else:
q_solid = 0
q_G = 0
if self.include_gravitational:
q_G_term = min((4 / 15) * np.pi * self.G * self.rho_c * self.Delta_rho * self.R_icb ** 2, 1e20)
q_G = q_G_term
q_L = self.rho_c * self.L
dc_dt = (q_liquid - q_solid + q_G) / max(q_L, 1e-10)
return np.clip(dc_dt, -1e-10, 1e-10)
except Exception as e:
return 0.0
def _update_core_temperature_outward(self, dt):
"""更新向外凝固的核温度 - 增强数值稳定性"""
try:
T_new = self.T_core.copy()
solid_mask = self.r_core <= self.R_icb
if np.any(solid_mask):
r_solid = self.r_core[solid_mask]
T_solid = self.T_core[solid_mask]
# 固态区热传导
alpha = self.kappa_s * dt / max(self.dr_core ** 2, 1e-20)
for i in range(1, len(r_solid) - 1):
r = max(r_solid[i], 1e-10)
d2T = (T_solid[i + 1] - 2 * T_solid[i] + T_solid[i - 1]) / max(self.dr_core ** 2, 1e-20)
dT = (T_solid[i + 1] - T_solid[i - 1]) / max(2 * self.dr_core, 1e-10)
temp_change = self.kappa_s * dt * (d2T + (2 / r) * dT)
T_new[i] = T_solid[i] + np.clip(temp_change, -100, 100)
T_new[0] = self.TL_0
T_new[np.sum(solid_mask) - 1] = self.TL_b
# 液态区绝热分布
liquid_mask = self.r_core > self.R_icb
if np.any(liquid_mask):
r_liquid = self.r_core[liquid_mask]
for i, r in enumerate(r_liquid):
exponent = min(self.nu_param * (self.R_icb ** 2 - r ** 2), 100)
T_new[np.sum(solid_mask) + i] = self.TL_b * np.exp(exponent)
return np.clip(T_new, 100, 10000)
except Exception as e:
return self.T_core
def _update_core_temperature_inward(self, dt):
"""更新向内凝固的核温度 - 增强数值稳定性"""
try:
T_new = self.T_core.copy()
liquid_mask = self.r_core < self.R_icb
if np.any(liquid_mask):
r_liquid = self.r_core[liquid_mask]
for i, r in enumerate(r_liquid):
exponent = min(self.nu_param * (self.R_core ** 2 - r ** 2), 100)
T_new[i] = self.TL_b * np.exp(exponent)
solid_mask = self.r_core >= self.R_icb
if np.any(solid_mask):
r_solid = self.r_core[solid_mask]
T_solid = self.T_core[solid_mask]
alpha = self.kappa_s * dt / max(self.dr_core ** 2, 1e-20)
start_idx = np.sum(liquid_mask)
for i in range(start_idx + 1, len(self.r_core) - 1):
r = max(self.r_core[i], 1e-10)
d2T = (T_solid[i - start_idx + 1] - 2 * T_solid[i - start_idx] +
T_solid[i - start_idx - 1]) / max(self.dr_core ** 2, 1e-20)
dT = (T_solid[i - start_idx + 1] - T_solid[i - start_idx - 1]) / max(2 * self.dr_core, 1e-10)
temp_change = self.kappa_s * dt * (d2T + (2 / r) * dT)
T_new[i] = T_solid[i - start_idx] + np.clip(temp_change, -100, 100)
T_new[start_idx] = self.TL_b
T_new[-1] = self.T_mantle[0]
return np.clip(T_new, 100, 10000)
except Exception as e:
return self.T_core
def _calculate_rayleigh_number(self):
"""计算瑞利数 - 增强数值稳定性"""
try:
delta_T = np.max(self.T_mantle) - np.min(self.T_mantle)
L = self.R_mercury - self.R_core
if delta_T <= 0:
return 1.0
Ra = (self.alpha_m * self.rho_m * self.G * delta_T * L ** 3 *
self.cp_m) / max(self.k_m * self.kappa_m, 1e-20)
return max(min(Ra, 1e20), 1.0)
except:
return 1.0
def _calculate_nusselt_number(self, Ra):
"""计算努塞尔数 - 增强数值稳定性"""
try:
if Ra <= 0:
return 1.0
Nu = 0.1 * Ra ** (1 / 3)
return max(min(Nu, 1e10), 1.0)
except:
return 1.0
def evolve(self, total_time=4.5):
"""演化模型 - 增强稳定性"""
total_time_seconds = total_time * 1e9 * 365.25 * 24 * 3600
n_steps = min(int(total_time_seconds / self.dt), 10000)
progress_bar = st.progress(0)
status_text = st.empty()
energy_initial = self._calculate_energy_balance()
# 重置稳定性标志
self.dt_stability_warned = False
self.dt_adjustment_count = 0
for step in range(n_steps):
current_time = step * self.dt / (1e9 * 365.25 * 24 * 3600)
if step % 100 == 0:
progress = min(step / n_steps, 1.0)
progress_bar.progress(progress)
status_text.text(f"演化进度: {current_time:.2f} Ga, ICB半径: {self.R_icb / 1000:.1f} km")
try:
# 检查时间步长调整次数限制
if self.dt_adjustment_count >= self.max_dt_adjustments:
if step == 0: # 只在第一步显示一次警告
st.warning(f"时间步长已自动调整{self.dt_adjustment_count}次,使用当前步长继续计算")
break
# 更新温度场
self.T_mantle = self._solve_mantle_heat_conduction(self.dt)
if self.solidification_mode == 'outward':
self.T_core = self._update_core_temperature_outward(self.dt)
dc_dt = self._calculate_phase_boundary_velocity_outward(self.dt)
else:
self.T_core = self._update_core_temperature_inward(self.dt)
dc_dt = self._calculate_phase_boundary_velocity_inward(self.dt)
# 更新相变边界
self.R_icb += dc_dt * self.dt
# 边界检查
if self.solidification_mode == 'outward':
self.R_icb = min(self.R_icb, 0.99 * self.R_core)
self.R_icb = max(self.R_icb, 0.01 * self.R_core)
else:
self.R_icb = max(self.R_icb, 0.01 * self.R_core)
self.R_icb = min(self.R_icb, 0.99 * self.R_core)
# 记录结果
if step % 10 == 0:
self._record_results(current_time, dc_dt, energy_initial)
# 终止条件
if ((self.R_icb >= 0.99 * self.R_core and self.solidification_mode == 'outward') or
(self.R_icb <= 0.01 * self.R_core and self.solidification_mode == 'inward') or
current_time >= total_time):
break
except Exception as e:
st.warning(f"步骤 {step} 失败: {str(e)}")
if step > 100: # 如果已经运行了一些步骤,可以提前结束
break
progress_bar.progress(1.0)
status_text.text("演化完成!")
# 显示时间步长调整摘要
if self.dt_adjustment_count > 0:
st.info(
f"时间步长自动调整: 从 {self.original_dt:.2e} 秒调整为 {self.dt:.2e} 秒,共调整{self.dt_adjustment_count}次")
def _record_results(self, current_time, dc_dt, energy_initial):
"""记录结果"""
self.results['time'].append(current_time)
self.results['icb_radius'].append(self.R_icb)
self.results['t_center'].append(self.T_core[0])
self.results['t_icb'].append(self.TL_b)
self.results['t_cmb'].append(self.T_core[-1])
self.results['solidification_rate'].append(dc_dt)
self.results['time_steps'].append(self.dt) # 记录实际使用的时间步长
Ra = self._calculate_rayleigh_number()
Nu = self._calculate_nusselt_number(Ra)
self.results['ra_mantle'].append(Ra)
self.results['nu_mantle'].append(Nu)
# CMB热流
try:
q_cmb = -self.k_m * (self.T_mantle[1] - self.T_mantle[0]) / max(self.dr_mantle, 1e-10)
self.results['q_cmb'].append(q_cmb)
except:
self.results['q_cmb'].append(0.0)
# 能量平衡
current_energy = self._calculate_energy_balance()
if energy_initial > 0:
energy_balance = abs(current_energy - energy_initial) / energy_initial
else:
energy_balance = 0.0
self.results['energy_balance'].append(min(energy_balance, 10.0)) # 限制最大误差
# 温度剖面
temp_profile = {
'r_core': self.r_core.copy(),
'T_core': self.T_core.copy(),
'r_mantle': self.r_mantle.copy(),
'T_mantle': self.T_mantle.copy(),
'R_icb': self.R_icb
}
self.results['temperature_profiles'].append(temp_profile)
def export_to_hdf5(self, filename):
"""导出结果到HDF5文件"""
try:
with h5py.File(filename, 'w') as f:
# 保存主要结果
for key, value in self.results.items():
if key != 'temperature_profiles' and value:
f.create_dataset(key, data=np.array(value))
# 保存温度剖面
if self.results['temperature_profiles']:
profiles_grp = f.create_group('temperature_profiles')
for i, profile in enumerate(self.results['temperature_profiles']):
time_grp = profiles_grp.create_group(f'time_{i}')
for key, value in profile.items():
time_grp.create_dataset(key, data=value)
# 保存模型参数
params_grp = f.create_group('model_parameters')
for key, value in self.__dict__.items():
if not key.startswith('_') and not callable(value) and key != 'results':
try:
if isinstance(value, (int, float, str, bool, np.number)):
params_grp.attrs[key] = value
except:
pass
except Exception as e:
st.error(f"导出HDF5文件失败: {str(e)}")
def run_single_model(model_name, mesh_size, time_step):
"""运行单个模型"""
try:
model = MercuryThermalModel(model_name, mesh_size, time_step)
model.evolve(4.5)
return model_name, model
except Exception as e:
st.error(f"模型 {model_name} 运行失败: {str(e)}")
return model_name, None
def setup_chinese_font():
"""设置中文字体"""
try:
plt.rcParams['font.family'] = ['DejaVu Sans', 'SimHei', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
except Exception as e:
plt.rcParams['font.family'] = 'DejaVu Sans'
plt.rcParams['axes.unicode_minus'] = False
def safe_log_plot(ax, x, y, **kwargs):
"""安全地对数绘图,避免数值问题"""
try:
# 过滤掉非正值和无穷大
mask = (np.array(y) > 0) & np.isfinite(y)
if np.any(mask):
x_filtered = np.array(x)[mask]
y_filtered = np.array(y)[mask]
ax.semilogy(x_filtered, y_filtered, **kwargs)
except Exception as e:
# 使用线性坐标作为备选
ax.plot(x, y, **kwargs)
def create_visualization(models_dict):
"""创建可视化图表"""
if not models_dict:
st.warning("没有模型结果可显示")
return
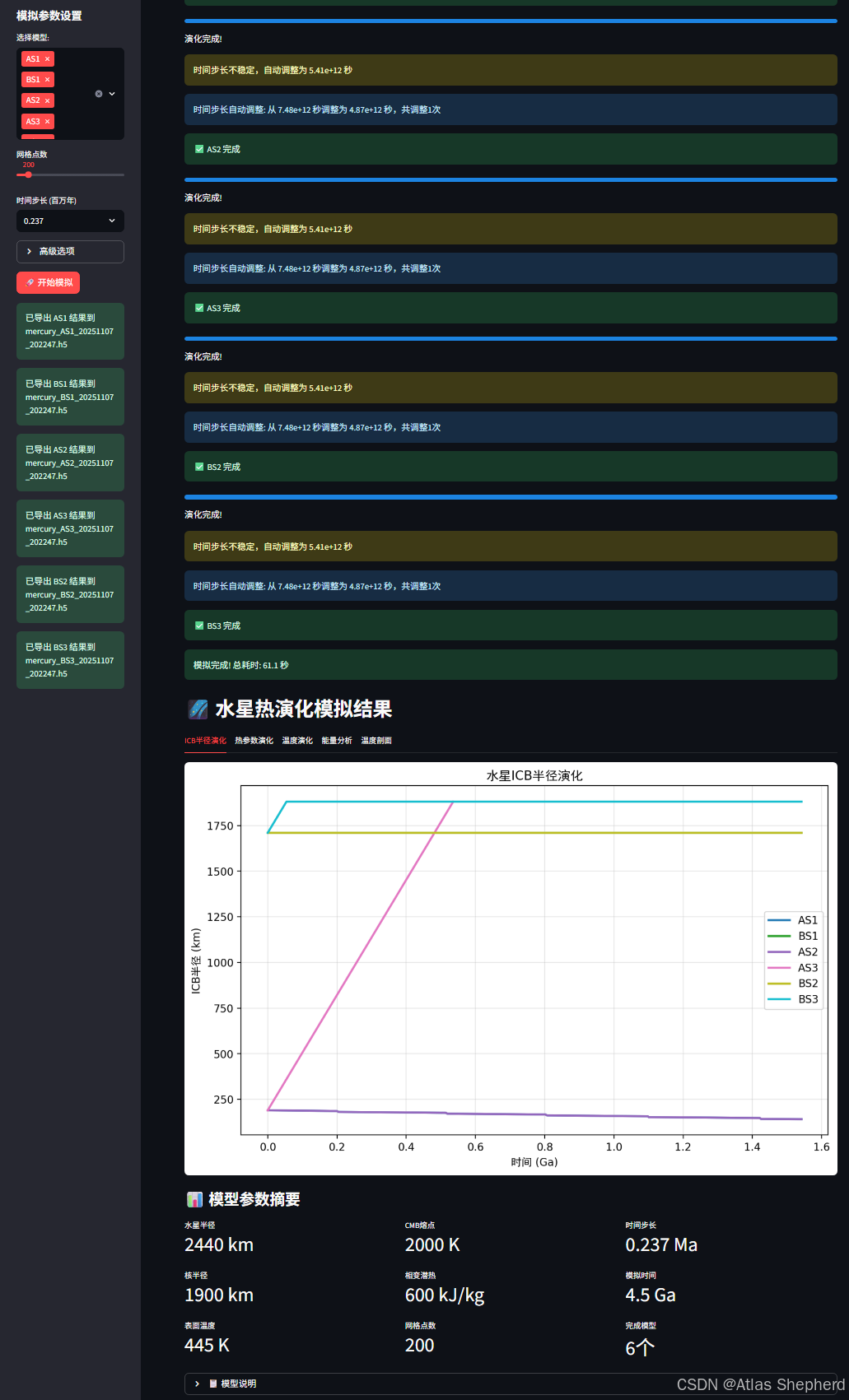
st.header("🌌 水星热演化模拟结果")
# 创建标签页
tab1, tab2, tab3, tab4, tab5 = st.tabs([
"ICB半径演化", "热参数演化", "温度演化", "能量分析", "温度剖面"
])
colors = plt.cm.tab10(np.linspace(0, 1, len(models_dict)))
with tab1:
fig, ax = plt.subplots(figsize=(10, 6))
for i, (name, model) in enumerate(models_dict.items()):
time_ga = model.results['time']
icb_km = [r / 1000 for r in model.results['icb_radius']]
ax.plot(time_ga, icb_km, label=name, color=colors[i], linewidth=2)
ax.set_xlabel('时间 (Ga)')
ax.set_ylabel('ICB半径 (km)')
ax.set_title('水星ICB半径演化')
ax.legend()
ax.grid(True, alpha=0.3)
st.pyplot(fig)
with tab2:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
for i, (name, model) in enumerate(models_dict.items()):
time_ga = model.results['time']
ra = model.results['ra_mantle']
nu = model.results['nu_mantle']
safe_log_plot(ax1, time_ga, ra, label=name, color=colors[i])
safe_log_plot(ax2, time_ga, nu, label=name, color=colors[i])
ax1.set_xlabel('时间 (Ga)')
ax1.set_ylabel('瑞利数 Ra')
ax1.set_title('幔瑞利数演化')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax2.set_xlabel('时间 (Ga)')
ax2.set_ylabel('努塞尔数 Nu')
ax2.set_title('幔努塞尔数演化')
ax2.legend()
ax2.grid(True, alpha=0.3)
st.pyplot(fig)
with tab3:
fig, ax = plt.subplots(figsize=(10, 6))
for i, (name, model) in enumerate(models_dict.items()):
time_ga = model.results['time']
t_center = model.results['t_center']
t_cmb = model.results['t_cmb']
ax.plot(time_ga, t_center, label=f'{name}-中心温度',
color=colors[i], linestyle='-')
ax.plot(time_ga, t_cmb, label=f'{name}-CMB温度',
color=colors[i], linestyle='--')
ax.set_xlabel('时间 (Ga)')
ax.set_ylabel('温度 (K)')
ax.set_title('水星内部温度演化')
ax.legend()
ax.grid(True, alpha=0.3)
st.pyplot(fig)
with tab4:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
for i, (name, model) in enumerate(models_dict.items()):
time_ga = model.results['time']
energy_balance = model.results['energy_balance']
q_cmb = model.results['q_cmb']
safe_log_plot(ax1, time_ga, energy_balance, label=name, color=colors[i])
ax2.plot(time_ga, q_cmb, label=name, color=colors[i])
ax1.set_xlabel('时间 (Ga)')
ax1.set_ylabel('相对能量误差')
ax1.set_title('能量守恒验证')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax2.set_xlabel('时间 (Ga)')
ax2.set_ylabel('CMB热流 (W/m²)')
ax2.set_title('核幔边界热流')
ax2.legend()
ax2.grid(True, alpha=0.3)
st.pyplot(fig)
with tab5:
model_name = st.selectbox('选择模型:', list(models_dict.keys()))
if model_name in models_dict:
model = models_dict[model_name]
time_points = model.results['time']
if time_points:
selected_time = st.slider('选择时间点 (Ga):',
min_value=float(min(time_points)),
max_value=float(max(time_points)),
value=float(min(time_points)))
time_idx = min(range(len(time_points)),
key=lambda i: abs(time_points[i] - selected_time))
profile = model.results['temperature_profiles'][time_idx]
fig, ax = plt.subplots(figsize=(10, 6))
r_core_km = profile['r_core'] / 1000
ax.plot(r_core_km, profile['T_core'], 'b-', label='核温度', linewidth=2)
r_mantle_km = profile['r_mantle'] / 1000
ax.plot(r_mantle_km, profile['T_mantle'], 'r-', label='幔温度', linewidth=2)
ax.axvline(x=profile['R_icb'] / 1000, color='k', linestyle='--', label='ICB')
ax.axvline(x=model.R_core / 1000, color='k', linestyle=':', label='CMB')
ax.set_xlabel('半径 (km)')
ax.set_ylabel('温度 (K)')
ax.set_title(f'{model_name}温度剖面 (t = {selected_time:.2f} Ga)')
ax.legend()
ax.grid(True, alpha=0.3)
st.pyplot(fig)
def main():
st.set_page_config(page_title="水星热演化数值模拟", layout="wide")
setup_chinese_font()
st.title("🌌 水星热演化核幔耦合数值模拟系统")
st.markdown("""
### 基于Williams(2009)理论的完整水星热演化数值模拟
- **AS系列**: 向外凝固模式
- **BS系列**: 向内凝固模式
- 完整物理过程实现,包含热传导、相变、对流等
""")
# 侧边栏
st.sidebar.header("模拟参数设置")
selected_models = st.sidebar.multiselect(
"选择模型:",
['AS1', 'AS2', 'AS3', 'BS1', 'BS2', 'BS3'],
default=['AS1', 'BS1']
)
mesh_size = st.sidebar.slider("网格点数", 100, 1000, 200)
time_step = st.sidebar.selectbox("时间步长 (百万年)", [0.237, 0.1185, 0.05925], index=0)
# 高级选项
with st.sidebar.expander("高级选项"):
enable_parallel = st.checkbox("启用并行计算", value=False)
export_results = st.checkbox("导出结果文件", value=True)
if st.sidebar.button("🚀 开始模拟", type="primary"):
if not selected_models:
st.error("请至少选择一个模型!")
return
models_dict = {}
start_time = time.time()
with st.spinner("正在进行数值计算..."):
if enable_parallel and len(selected_models) > 1:
try:
with ThreadPoolExecutor(max_workers=min(2, len(selected_models))) as executor:
futures = [executor.submit(run_single_model, name, mesh_size, time_step)
for name in selected_models]
for future in futures:
name, model = future.result()
if model:
models_dict[name] = model
st.success(f"✅ {name} 完成")
except Exception as e:
st.error(f"并行计算失败: {str(e)},回退到串行计算")
for name in selected_models:
name, model = run_single_model(name, mesh_size, time_step)
if model:
models_dict[name] = model
st.success(f"✅ {name} 完成")
else:
for name in selected_models:
with st.spinner(f"运行 {name} 模型..."):
name, model = run_single_model(name, mesh_size, time_step)
if model:
models_dict[name] = model
st.success(f"✅ {name} 完成")
elapsed_time = time.time() - start_time
st.success(f"模拟完成! 总耗时: {elapsed_time:.1f} 秒")
if models_dict:
try:
create_visualization(models_dict)
except Exception as e:
st.error(f"可视化创建失败: {str(e)}")
for name, model in models_dict.items():
st.subheader(f"{name} 模型结果")
col1, col2 = st.columns(2)
with col1:
st.metric("最终ICB半径", f"{model.results['icb_radius'][-1] / 1000:.1f} km")
st.metric("中心温度", f"{model.results['t_center'][-1]:.0f} K")
with col2:
st.metric("CMB温度", f"{model.results['t_cmb'][-1]:.0f} K")
st.metric("模拟步数", len(model.results['time']))
if export_results:
timestamp = datetime.now().strftime("%Y%m%d_%H%M%S")
for name, model in models_dict.items():
filename = f"mercury_{name}_{timestamp}.h5"
try:
model.export_to_hdf5(filename)
st.sidebar.success(f"已导出 {name} 结果到 {filename}")
except Exception as e:
st.error(f"导出 {name} 结果失败: {str(e)}")
st.subheader("📊 模型参数摘要")
col1, col2, col3 = st.columns(3)
with col1:
st.metric("水星半径", "2440 km")
st.metric("核半径", "1900 km")
st.metric("表面温度", "445 K")
with col2:
st.metric("CMB熔点", "2000 K")
st.metric("相变潜热", "600 kJ/kg")
st.metric("网格点数", f"{mesh_size}")
with col3:
st.metric("时间步长", f"{time_step} Ma")
st.metric("模拟时间", "4.5 Ga")
st.metric("完成模型", f"{len(models_dict)}个")
else:
st.error("没有模型成功完成")
with st.expander("📋 模型说明"):
st.markdown("""
**模型系列:**
- **AS系列 (向外凝固)**: 凝固从核中心向外进行
- **BS系列 (向内凝固)**: 凝固从核幔边界向内进行
**物理过程:**
- 热传导与对流
- 相变(凝固/熔化)
- 放射性元素衰变生热
- 引力势能释放
**数值稳定性改进:**
- 使用scipy.integrate.trapezoid替代弃用的np.trapz
- 添加数值溢出保护
- 限制指数函数参数范围
- 避免除以零错误
- **时间步长自动调整**: 自动检测并调整不稳定时间步长,避免警告刷屏
""")
if __name__ == "__main__":
main()