通俗易懂地理解深度遍历DFS、和广度遍历BFS

什么是遍历

在说深度遍历DFS、和广度遍历BFS之前，我们要先理解什么是遍历，以及遍历相关的知识点有哪些

数据遍历，顾名思义，就是按照一定的顺序，逐个访问或处理加工某个数据结构中的项
如遍历数组、遍历对象、遍历字符串、遍历Map、遍历Set（前端最常见的）
还可以遍历：
图（有向图、无向图、带权图、无权图）、
树（二叉树、N 叉树、决策树、ATS语法树 、DOM 树）
文件系统（递归遍历目录，从根目录开始查找文件）、
二维或三维网格、
网络与拓扑结构、
组合与排列问题等

常见的遍历方式

经典遍历：for, while, do...while
数组内置方法 (ES5+) ：forEach, map, filter, reduce, some, every, find, findIndex 等
数组内置方法 (ES5+)for...of 直接遍历值
类数组遍历方法：适用于非纯数组但有 length 属性的对象

类数组的遍历

最常见的比如是选中相同的dom元素进行遍历，如下：

方法1: Array.from把类数组，转数组

js 复制代码

// 
const nodeList = document.querySelectorAll('div');
Array.from(nodeList).forEach(node => {
  console.log(node);
});

方法2: 使用扩展运算符... 把类数组转成数组

js 复制代码

//  (ES6)
[...nodeList].forEach(node => {
  console.log(node);
});

方法3: 借用古老的 Array.prototype.slice.call 进行遍历

js 复制代码

Array.prototype.slice.call(nodeList).forEach(function(node) {
  console.log(node);
});

深度遍历DFS、和广度遍历BFS

所谓的深度遍历和广度遍历
通俗易懂地可以理解成为按照两种不同的套路进行遍历
深度遍历的套路是先纵再横（纵向到头）
广度遍历的套路是先横再纵（横向到头再纵向到下一层）
我们通过如下的数据结构演示一下

假设我们有一个数组，存放的是中国美国以及对应的下级行政单位，如下：

js 复制代码

let tree = 
[
    {
        name: '中国',
        id: '1',
        children: [
            {
                name: '北京',
                id: '1-1',
                children: [
                    {
                        name: '朝阳',
                        id: '1-1-1',
                        children: [
                            { name: '街道A', id: '1-1-1-1' },
                            { name: '街道B', id: '1-1-1-2' },
                        ]
                    },
                    {
                        name: '海淀',
                        id: '1-1-2',
                    },
                ]
            },
            {
                name: '上海',
                id: '1-2',
                children: [
                    {
                        name: '浦东',
                        id: '1-2-1',
                    },
                    {
                        name: '静安',
                        id: '1-2-2',
                    },
                ]
            },
        ]
    },
    {
        name: '美国',
        id: '2',
        children: [
            {
                name: '纽约',
                id: '2-1',
                children: [
                    {
                        name: '中城',
                        id: '2-1-1',
                    },
                    {
                        name: '下城',
                        id: '2-1-2',
                    },
                ]
            },
            {
                name: '洛杉矶',
                id: '2-2',
                children: [
                    {
                        name: '长滩',
                        id: '2-2-1',
                    },
                    {
                        name: '圣安娜',
                        id: '2-2-2',
                    },
                ]
            },
        ]
    }
]

深度遍历DFS示例

深度遍历，就是先纵向，先往下走，走到头，再回来最近的一层，再往下走。

对应遍历代码函数：

js 复制代码

// 深度遍历Deep First Search
function dfs(tree){
    tree.forEach((node, index)=>{
        console.log('深度遍历-->', node.name, node.id)
        if(node.children){
            dfs(node.children)
        }
    })
}
dfs(tree)

打印图：

如上图的打印结果，简单明了。

广度遍历BFS示例

而广度遍历，则是横着走，横着走到头了，再进入下一层，如下：

js 复制代码

// 广度遍历 Breadth First Search
function bfs(tree) {
    for (let i = 0; i < tree.length; i++) {
        let node = tree[i]
        console.log('node--->', node.name, node.id)
        if (node.children) {
            tree.push(...node.children)
        }
    }
    return tree
}
bfs(tree)

打印图：

对比上述的两个图，发现，的确是，一个是先纵再横，一个是先横再纵
是的，到这里，我们就入门了深度遍历和广度遍历
注意，只是入门

注意点：广度遍历之for循环length动态的，对比forEach的length固定的

上述的代码，能不能使用forEach呢？

js 复制代码

tree.forEach((node)=>{
    console.log('node', node.name, node.id)
    if(node.children){
        tree.push(...node.children)
    }
})

答案是不行的

forEach循环范围，在初始化时就固定了
初始的时候，数组多长，就会遍历多少个元素
就算是在循环的过程中，添加元素项，也是不行的
新添加的元素项，不会被遍历，如下：

js 复制代码

let arr = [1, 2];
arr.forEach((item, index) => {
    console.log('处理:', item);
    if (item === 1) {
        arr.push(3);
    }
});
// 输出：
// 处理: 1
// 处理: 2
// 注意！！！：3 不会被输出！

虽然 3 被 push 进去了，但 forEach 不会去处理它，因为它只遍历原始长度（2）的元素

但是，for循环，却是可以处理这种动态添加项，修改数组length的操作

js 复制代码

for (let i = 0; i < tree.length; i++) {
    // 每次循环都重新读取 tree.length
    // 如果 tree.length 变了（push 了新元素），i 会继续增加直到新的长度
}

所以，就广度遍历而言，不能用forEach去遍历操作

一般而言，forEach只是适合遍历固定长度的静态数组、不修改数组结构相关的操作，比如：

tree.forEach(node => console.log(node.name))

深度遍历的本质，是调用栈

所谓的栈，就是先进后出，走到底，再回溯。
这里不赘述枯燥概念
实际上浏览器也能直观地看到本案例中的，深度遍历的，调用栈

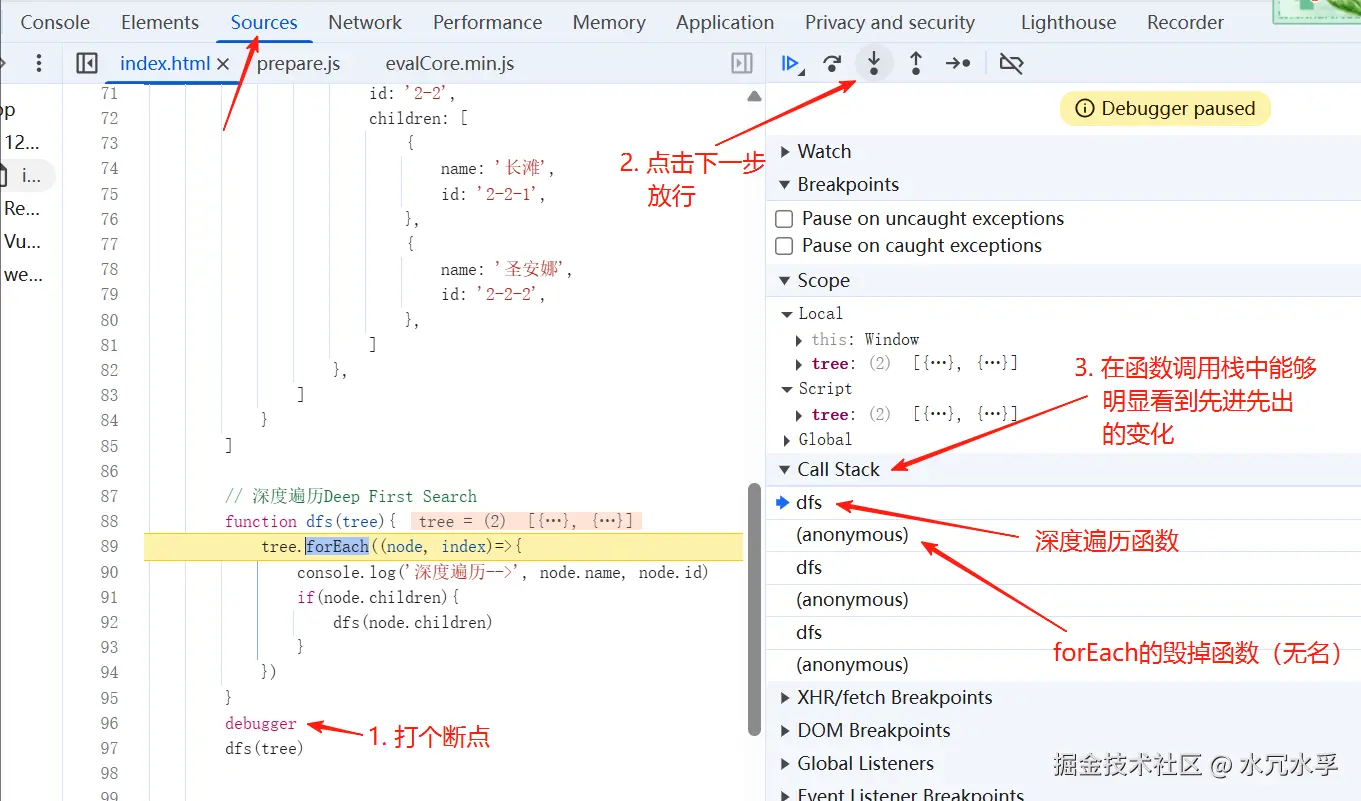
如上图，调用栈中，有多个dfs调用函数，最后随着断点的进行，会越来越少，最后清空调用栈
如果大家，debugger一下广度遍历，会发现，Call Stack中
只有一个dfs函数**（广度遍历的本质是队列）**

如下：

js 复制代码

function dfsStack(tree) {
    const result = [];
    const stack = [...tree]; // 使用数组模拟栈，拷贝一份
    while (stack.length > 0) {
        const node = stack.pop(); // 栈顶取出（栈会少一项，少的项会赋值在node变量上）
        result.push(node); // 存数据
        // 逆序压入子节点，保证左子树先被访问(倒着遍历)
        // 栈是先进后出，后进先出，想让哪个节点先被访问，就得让它最后入栈
        if (node.children && node.children.length > 0) {
            for (let i = node.children.length - 1; i >= 0; i--) {
                stack.push(node.children[i]);
            }
        }
    }
    return result;
}

广度遍历的本质是队列

和栈不同，队列是先进先出，如下代码：

js 复制代码

function bfs(tree) {

    const queue = [...tree]; // 初始化队列：将根节点们放入队列
    const result = [];       // 收集遍历结果

    while (queue.length > 0) {
        // 1. 从队列头部取出节点（先进先出）
        const node = queue.shift(); // 队列操作：取头元素

        // 2. 访问当前节点
        console.log('node--->', node.name, node.id);
        result.push(node);

        // 3. 将当前节点的子节点依次加入队列尾部，这样可一层层地平推下去
        if (node.children && node.children.length > 0) {
            // 正序添加子节点（从左到右）
            for (let i = 0; i < node.children.length; i++) {
                queue.push(node.children[i]); //队列操作：加到末尾
            }
        }
    }
    return result; // 返回遍历结果
}

// 调用
bfs(tree);

深度遍历DFS、和广度遍历BFS的前端应用场景

文章末尾，再总结一下，从前端角度而言，深度遍历DFS、和广度遍历BFS的具体应用场景

如果深度极大但宽度很小的树（如单链表），DFS 更省内存；
如果宽度极大但深度很小的树（如扁平结构），BFS 更有优势
如果只要求，访问所有节点，而不关心顺序和效率时，二者可以随意地替换
具体的前端代码中的常见场景有：
*
1. DOM树操作和遍历
- 1. 组件树的递归渲染
- 1. 文件目录树的展示
- 1. 无限级联选择器（递归组件）
- 1. 等等...

A good memory is better than a bad pen. Record it down...