总的来说,因子投资方法可以分为以下 6 个类别:排序法、回归方法检验因子模型、检验异象、比较多因子模型、因子正交化、广义矩估计(GMM)。
多因子模型比较
多因子模型本质上是"不完美"的近似,但其中一些模型因其因子具备可靠的经济学或行为金融学基础、能够代表系统性风险源,并显著提升对资产预期收益率的解释力,因而是"有用"的。随着因子数量的不断增加,如何系统、科学地比较不同的多因子模型,已成为实证资产定价研究的核心议题之一。
多因子模型的比较可从"两个目标、两个切入点、多种方法"这一逻辑主线展开:
两个目标:
- 检验模型对一组外生测试资产(test assets)的定价能力;
- 检验模型是否能够解释其他竞争性模型中的因子收益。
两个切入点:
- 联合检验:考察所有测试资产的定价误差是否联合为零;
- 独立检验:分别考察每个资产的定价误差是否为零。
基于不同切入点,可采用不同的统计方法:若关注联合检验,可使用GRS检验或均值-方差张成检验;若关注独立误差,则可使用α检验。需注意的是,无论被解释对象是测试资产还是其他模型的因子,这些方法在统计本质上是一致的。因此,下文将按检验方法的类型进行阐述,并在必要时强调其应用场景。
以下各节将依次介绍GRS检验、均值-方差张成检验、α检验及贝叶斯方法,并从几何视角对前两种方法进行对比,以深化理解。
GRS检验
GRS检验由Gibbons、Ross与Shanken提出,是一种基于有限样本理论的联合检验方法。假设有 <math xmlns="http://www.w3.org/1998/Math/MathML"> N N </math>N 个测试资产,待检验模型包含 <math xmlns="http://www.w3.org/1998/Math/MathML"> K K </math>K 个因子。定义:
- <math xmlns="http://www.w3.org/1998/Math/MathML"> α ^ = [ α ^ 1 , α ^ 2 , ... , α ^ N ] ⊤ \hat{\alpha} = [\hat{\alpha}_1, \hat{\alpha}_2, \ldots, \hat{\alpha}_N]^\top </math>α^=[α^1,α^2,...,α^N]⊤:定价误差向量;
- <math xmlns="http://www.w3.org/1998/Math/MathML"> Σ ^ \hat{\Sigma} </math>Σ^:残差协方差矩阵的估计;
- <math xmlns="http://www.w3.org/1998/Math/MathML"> Ω ^ \hat{\Omega} </math>Ω^:因子收益率协方差矩阵的估计;
- <math xmlns="http://www.w3.org/1998/Math/MathML"> μ ^ f \hat{\mu}_f </math>μ^f:因子预期收益率向量。
则GRS统计量为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> GRS = T − N − K N ( 1 + μ ^ f ⊤ Ω ^ − 1 μ ^ f ) − 1 α ^ ⊤ Σ ^ − 1 α ^ ∼ F N , T − N − K \text{GRS} = \frac{T - N - K}{N} \left(1 + \hat{\mu}_f^\top \hat{\Omega}^{-1} \hat{\mu}f\right)^{-1} \hat{\alpha}^\top \hat{\Sigma}^{-1} \hat{\alpha} \sim F{N, T-N-K} </math>GRS=NT−N−K(1+μ^f⊤Ω^−1μ^f)−1α^⊤Σ^−1α^∼FN,T−N−K
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> T T </math>T 为时间序列长度。
优点与局限
优点:
- 精确的有限样本分布,不依赖渐近理论;
- 检验效力高。
局限:
- 需假设收益率服从多元正态分布;
- 要求 <math xmlns="http://www.w3.org/1998/Math/MathML"> T > N + K T > N + K </math>T>N+K,否则无法计算逆矩阵。
尽管存在局限,GRS检验在学术界仍被广泛使用。例如,Liu et al.(2019)通过GRS检验比较了针对A股市场构建的三因子模型与Fama-French三因子模型,发现前者能够解释后者的因子收益,反之则不成立,从而支持中国版模型更适用。
几何解释
GRS统计量可改写为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> GRS = T − N − K N ( 1 + θ ^ N + K 2 1 + θ ^ K 2 − 1 ) \text{GRS} = \frac{T - N - K}{N} \left( \frac{1 + \hat{\theta}_{N+K}^2}{1 + \hat{\theta}_K^2} - 1 \right) </math>GRS=NT−N−K(1+θ^K21+θ^N+K2−1)
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ ^ K \hat{\theta}K </math>θ^K 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ ^ N + K \hat{\theta}{N+K} </math>θ^N+K分别表示仅由因子和由因子与测试资产共同构成的最大夏普比率组合的事后夏普比率。该统计量实质上检验了加入测试资产后能否显著提升投资组合的夏普比率。
均值-方差张成检验
均值-方差张成检验由Huberman与Kandel提出,基于Markowitz资产组合理论,检验加入新资产后是否能够扩展原因子组合的有效前沿。
设 <math xmlns="http://www.w3.org/1998/Math/MathML"> R 1 R_1 </math>R1 为 <math xmlns="http://www.w3.org/1998/Math/MathML"> K K </math>K 个因子的收益向量, <math xmlns="http://www.w3.org/1998/Math/MathML"> R 2 R_2 </math>R2 为 <math xmlns="http://www.w3.org/1998/Math/MathML"> N N </math>N 个测试资产的收益向量。定义总体收益向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> R = [ R 1 ⊤ , R 2 ⊤ ] ⊤ R = [R_1^\top, R_2^\top]^\top </math>R=[R1⊤,R2⊤]⊤,其期望与协方差矩阵为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> μ = [ μ 1 μ 2 ] , Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] \mu = \begin{bmatrix} \mu_1 \\ \mu_2 \end{bmatrix}, \quad \Sigma = \begin{bmatrix} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix} </math>μ=[μ1μ2],Σ=[Σ11Σ21Σ12Σ22]
通过建立线性模型:
<math xmlns="http://www.w3.org/1998/Math/MathML"> R 2 = α + β R 1 + ε R_2 = \alpha + \beta R_1 + \varepsilon </math>R2=α+βR1+ε
可导出张成检验的原假设:
<math xmlns="http://www.w3.org/1998/Math/MathML"> H 0 : α = 0 and β 1 K = 1 N H_0: \alpha = 0 \quad \text{and} \quad \beta \mathbf{1}_K = \mathbf{1}_N </math>H0:α=0andβ1K=1N
若原假设成立,则测试资产不改变原因子组合的前沿。
检验统计量
Kan and Zhou(2012)提出了三种渐近等价的统计量:似然比(LR)、Wald(W)和拉格朗日乘子(LM)统计量,均渐近服从 <math xmlns="http://www.w3.org/1998/Math/MathML"> χ 2 N 2 \chi^2_{2N} </math>χ2N2 分布。这些统计量可表示为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> L R = T [ ln ( 1 + s 1 ) + ln ( 1 + s 2 ) ] LR = T \left[ \ln(1 + s_1) + \ln(1 + s_2) \right] </math>LR=T[ln(1+s1)+ln(1+s2)]
<math xmlns="http://www.w3.org/1998/Math/MathML"> W = T ( s 1 + s 2 ) W = T (s_1 + s_2) </math>W=T(s1+s2)
<math xmlns="http://www.w3.org/1998/Math/MathML"> L M = T ( s 1 1 + s 1 + s 2 1 + s 2 ) LM = T \left( \frac{s_1}{1+s_1} + \frac{s_2}{1+s_2} \right) </math>LM=T(1+s1s1+1+s2s2)
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> s 1 s_1 </math>s1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> s 2 s_2 </math>s2 为两个前沿差异的度量。
应用举例
Han et al.(2016)利用该检验证明传统动量与反转因子无法解释其构建的"趋势因子",说明新因子提供了增量信息。
GRS与张成检验的几何比较
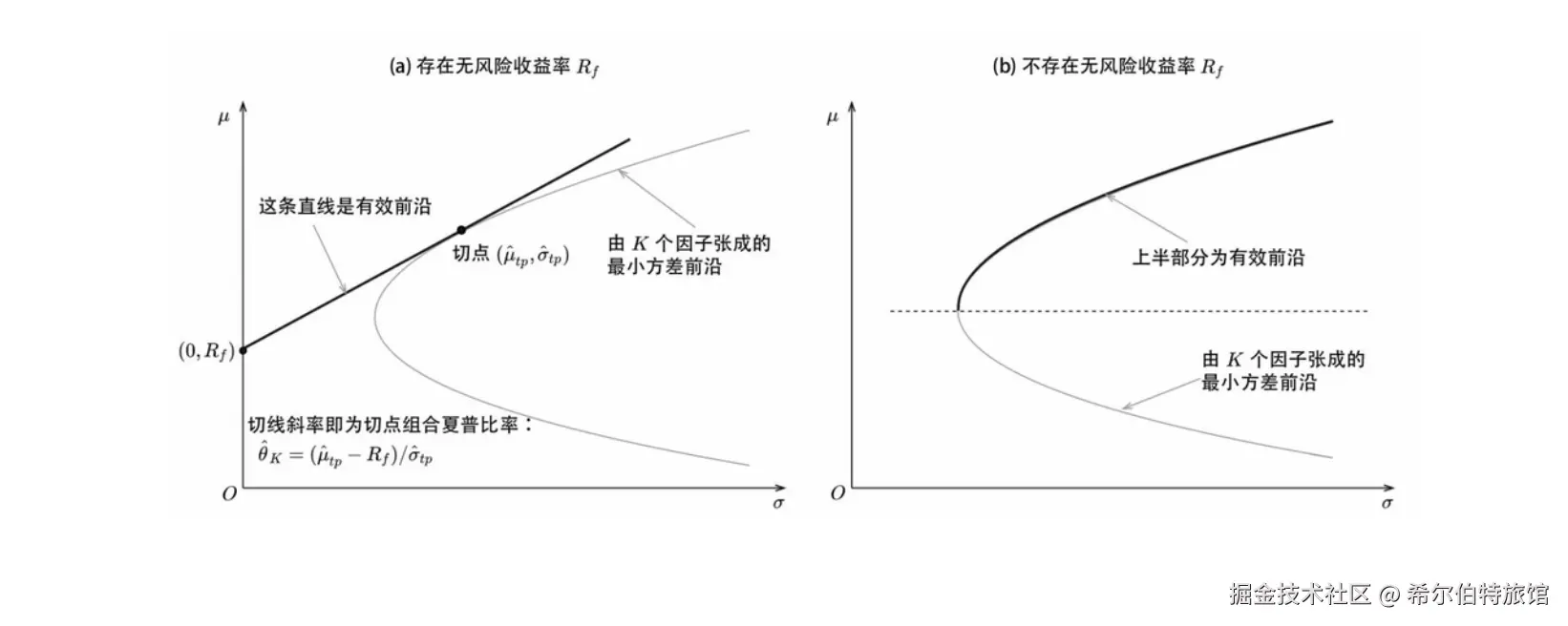
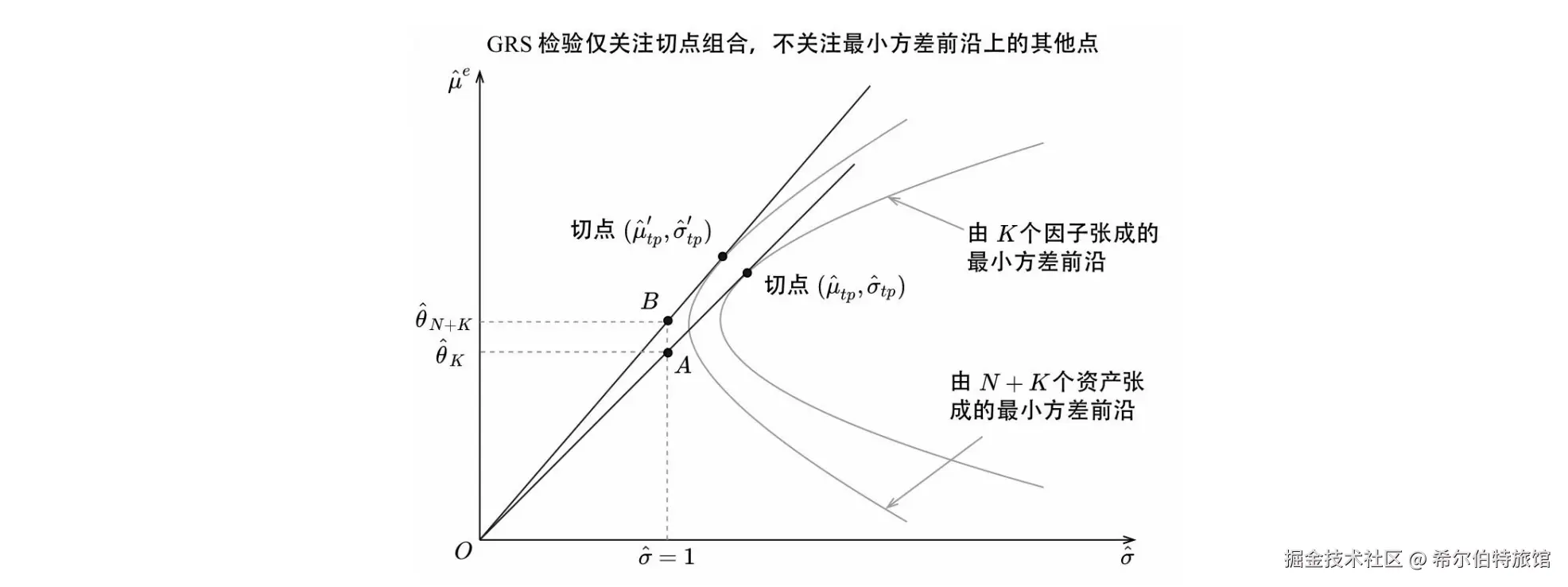
GRS检验假设存在无风险资产,仅关注切点组合的夏普比率提升;而均值-方差张成检验不要求无风险资产,关注整个有效前沿的扩展。
从几何角度看:
- GRS检验比较的是有无测试资产时的夏普比率差异;
- 张成检验则通过比较全局最小方差组合和特定切线组合,综合评估前沿的整体改进。
Kan and Zhou(2012)给出了有限样本下LR统计量的几何表达式:
<math xmlns="http://www.w3.org/1998/Math/MathML"> L R = T − K − N N [ ( σ g , K σ g , N + K ) ( L N + K L K ) − 1 ] LR = \frac{T - K - N}{N} \left[ \left( \frac{\sigma_{g,K}}{\sigma_{g,N+K}} \right) \left( \frac{L_{N+K}}{L_K} \right) - 1 \right] </math>LR=NT−K−N[(σg,N+Kσg,K)(LKLN+K)−1]
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> σ g , ⋅ \sigma_{g,\cdot} </math>σg,⋅ 为全局最小方差组合的标准差, <math xmlns="http://www.w3.org/1998/Math/MathML"> L L </math>L 为相应切线组合的斜率长度。

α检验
α检验是一种直接且广泛使用的方法,它独立检验每个资产的定价误差:
- 对每个测试资产,将其超额收益对因子收益进行时序回归,得到 <math xmlns="http://www.w3.org/1998/Math/MathML"> α i \alpha_i </math>αi 及其标准误(通常经Newey-West调整);
- 计算每个 <math xmlns="http://www.w3.org/1998/Math/MathML"> α i \alpha_i </math>αi 的 t 统计量;
- 计算所有 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ α i ∣ |\alpha_i| </math>∣αi∣ 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ t ( α i ) ∣ |t(\alpha_i)| </math>∣t(αi)∣ 的均值,作为模型误定价程度的综合指标。
α检验直观易行,常与GRS检验结合使用,如Hou et al.(2015)和Fama and French(2020)所示。
贝叶斯方法
Barillas and Shanken(2018)提出了基于贝叶斯因子的模型比较方法。在该框架下,不同模型的后验概率比取决于其边际似然(marginal likelihood):
<math xmlns="http://www.w3.org/1998/Math/MathML"> P ( M i ∣ D ) P ( M j ∣ D ) = P ( M i ) ⋅ P ( D ∣ M i ) P ( M j ) ⋅ P ( D ∣ M j ) \frac{P(M_i \mid D)}{P(M_j \mid D)} = \frac{P(M_i) \cdot P(D \mid M_i)}{P(M_j) \cdot P(D \mid M_j)} </math>P(Mj∣D)P(Mi∣D)=P(Mj)⋅P(D∣Mj)P(Mi)⋅P(D∣Mi)
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( D ∣ M i ) P(D \mid M_i) </math>P(D∣Mi) 为模型 <math xmlns="http://www.w3.org/1998/Math/MathML"> M i M_i </math>Mi 的边际似然。若假设模型先验相等,则贝叶斯因子(即边际似然比)决定模型优劣。
然而,Chib et al.(2020)指出该方法在先验设定上存在缺陷,尤其当模型参数空间或先验常数不一致时,边际似然比较可能失效。他们提出了修正先验分布的改进方法。
尽管存在争议,贝叶斯方法为模型选择提供了另一种思路,如Stambaugh and Yuan(2017)应用该方法比较了多个因子模型。
小结
多因子模型的比较需综合运用多种统计方法,兼顾联合检验与独立检验,并考虑有限样本性质与分布假设。GRS检验、均值-方差张成检验和α检验已成为标准工具;贝叶斯方法虽具潜力,但尚待进一步验证。在实践中,建议同时使用多种方法,并结合经济理论进行综合判断,以提升结论的稳健性。