一. 核心思想
贝叶斯分类是一类基于贝叶斯定理(Bayes' Theorem)和概率统计的分类算法,核心思想是 "通过已知的先验概率,结合数据的似然性,计算后验概率,最终将样本归为后验概率最高的类别"。它在机器学习、模式识别等领域应用广泛(如垃圾邮件过滤、疾病诊断、文本分类等),尤其适合处理 "样本量较小" 或 "需要利用先验知识" 的场景。
二. 理论基础
1. 定义:
对于二分类或者多分类问题,若用C表示"类别",用X表示"样本特征",则贝叶斯定理公式为
其中每部分含义如下:
|-------------|--------------------------------------------------|
| 后验概率P(C|X) | 已知样本特征 X 时,样本属于类别 C 的概率("看到特征后,判断类别的置信度") |
| 似然性P(X|C) | 已知类别为 C 时,样本出现特征 X 的概率("类别为 C 的样本,恰好具备这些特征的可能性") |
| 先验概率 P(C) | 未看样本特征时,类别 C 本身的概率 |
| 证据因子 P(X) | 样本特征 X 出现的总概率(与类别无关,仅用于 "归一化",确保后验概率总和为 1) |
2. 分类逻辑:
贝叶斯分类的核心规则是 "最大后验概率准则 ": 对一个待分类样本 X,计算它属于所有可能类别的后验概率,比如对于 这些类别分别计算
,最终将 X 归为后验概率最大的类别。
由于P(X)对所有类别相同,实际计算时可简化为:
三. 经典算法--朴素贝叶斯(Native Bayes)
1.问题背景:
直接应用贝叶斯定理时,若样本特征 X 是 "多维度特征"(如文本分类中,X 包含 "是否含'中奖'""是否含'点击'" 等多个特征),计算P(X|C)会面临 "维度灾难"------ 需统计所有特征组合的概率,数据量不足时根本无法实现。
2. 核心思想:
引入"特征条件独立" 的核心假设,也就是朴素贝叶斯的 "朴素(Naive)" 体现在:假设在已知类别的前提下,样本的各个特征之间是相互独立的 。
即对于类别 C 和多维度特征 (
是第 i 个特征),有:
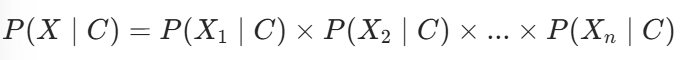
通过引入这个假设,大幅简化了计算,也就是无需统计 "特征组合的概率",只需单独统计 "每个特征在某类别下的概率" 即可。
3. 文本分类之"垃圾邮件过滤"
设类别C1为垃圾邮件,C2为正常邮件,X为邮件中的关键词,朴素贝叶斯分类过程如下:
a. 数据预处理:将文本转为特征,每个邮件对应一个向量X,向量的每个维度代表一个关键词;
b. 计算先验概率P(C):根据训练集统计类别概率,对于第k类计算如下:
c. 计算似然性P(X|C):统计类别k中特征Xi出现的概率,计算如下:
注意:这里使用了拉普拉斯平滑,避免概率为0,分母加2是因为这里是个二分类问题。
d.计算后验概率并分类:对于测试邮件X,分别计算P(C1|X)、P(C2|X),若前者大,则判定为垃圾邮件,否则为正常邮件。
四.朴素贝叶斯常见变体
|--------------|-----------------------|--------------------------------------------|
| 类型 | 使用特征 | 核心假设 |
| 高斯朴素贝叶斯 | 连续型特征 | 假设 "类别k下的特征Xi服从高斯分布(正态分布)",通过样本均值和方差估算似然函数 |
| 多项式朴素贝叶斯 | 离散型特征 | 假设 "类别k下的特征Xi 服从多项式分布",常用于 "特征是计数数据" 的场景 |
| 伯努利朴素贝叶斯 | |--------| | 二值离散特征 | | 假设 "类别k下的特征Xi服从伯努利分布",仅关注 "特征是否出现"(而非出现次数) |
五.优缺点
1. 优点
- 计算高效:仅需统计先验概率和似然性,复杂度低,适合大规模数据或实时场景;
- 数据需求少:依赖先验知识,小样本下也能工作(尤其适合样本难以获取的场景);
- 可解释性强:结果是 "类别概率",能直观体现分类的置信度;
- 抗过拟合能力强:假设简单,不易过度依赖训练集的噪声数据。
2. 缺点
- "特征独立" 假设理想化:实际场景中,特征往往存在相关性(如 "邮件含'中奖'和'点击链接'高度相关"),会导致似然性计算不准,影响分类效果;
- 对先验概率敏感:若先验概率统计偏差大(如训练集类别分布与真实场景差异大),会严重影响后验概率的准确性;
- 无法处理 "特征值为 0" 的极端情况:需依赖拉普拉斯平滑等方法修正,否则可能出现概率为 0 的情况,导致分类失效。
----- 以上为本人学习机器学习这门课总结出的一些知识点,有错误或者疑问可以评论区交流,欢迎指正!!!