深度学习核心损失函数详解：交叉熵、MSE、对比学习（InfoNCE）

本文将用代码、图表和比喻，带你彻底理解这三种驱动AI模型的损失函数。

1. 交叉熵损失 (Cross-Entropy Loss)：分类任务的"黄金标准"

核心思想 ：衡量模型输出的预测概率分布 与真实概率分布之间的差异。差异越小，损失越小。

真实分布 ：通常是 one-hot 编码（如 [1, 0, 0] 代表"猫"）。
预测分布 ：模型通过 Softmax 函数输出的概率（如 [0.7, 0.2, 0.1]）。

直观比喻 ：

老师（真实分布）知道正确答案是A。学生（模型）提交了一份选择题的概率答案。交叉熵就是评判学生答案的"离谱程度"。如果学生坚定地选错了（如给错误答案D分配0.9的概率），惩罚会非常严厉；如果学生不确定（如正确答案A只有0.4的概率），也会受到惩罚，但没那么重。

公式（多分类） ：
L=−∑c=1Myclog⁡(pc)L = -\sum_{c=1}^{M} y_c \log(p_c)L=−∑c=1Myclog(pc)

其中 ycy_cyc 是真实标签在类别 ccc 上的值（0或1），pcp_cpc 是预测属于类别 ccc 的概率。

代码与深度解释：

python 复制代码

import torch
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as np

# 设置随机种子以保证结果可重现
torch.manual_seed(42)

# 模拟一个3分类问题，Batch Size=2
logits = torch.tensor([[2.0, 1.0, 0.1],  # 模型输出的原始分数 (logits)
                       [0.5, 3.0, 0.5]])
labels = torch.tensor([0, 1]) # 样本0的真实类别是0，样本1的真实类别是1

# 方法1：使用PyTorch内置函数 (推荐)
# nn.CrossEntropyLoss = nn.LogSoftmax + nn.NLLLoss
# 所以直接输入logits即可，不需要手动做Softmax
ce_loss = nn.CrossEntropyLoss()
loss = ce_loss(logits, labels)
print(f"PyTorch CrossEntropy Loss: {loss.item():.4f}")

# 方法2：分步手动计算，彻底理解过程
def manual_ce(logits, labels):
    # 1. Softmax: 将logits转换为概率分布
    probabilities = F.softmax(logits, dim=1)
    print(f"Probabilities: {probabilities}")

    # 2. Log Softmax: 计算概率的对数 (稳定性更好)
    log_probs = F.log_softmax(logits, dim=1)
    print(f"Log Probabilities: {log_probs}")

    # 3. NLLLoss: 根据真实标签，取出对应类别的对数概率
    # 对于样本0，取第0个类别的log prob；样本1，取第1个类别的log prob
    nll_loss = -log_probs[torch.arange(len(logits)), labels]
    print(f"Loss per sample: {nll_loss}")

    # 4. 求平均
    return nll_loss.mean()

manual_loss = manual_ce(logits, labels)
print(f"Manual CrossEntropy Loss: {manual_loss.item():.4f}\n")

输出：

复制代码

PyTorch CrossEntropy Loss: 0.2845
Probabilities: tensor([[0.6590, 0.2424, 0.0986],
        [0.0705, 0.8590, 0.0705]])
Log Probabilities: tensor([[-0.4170, -1.4170, -2.3170],
        [-2.6520, -0.1520, -2.6520]])
Loss per sample: tensor([0.4170, 0.1520])
Manual CrossEntropy Loss: 0.2845

图表与洞察：

python 复制代码

# 展示"预测正确类别的概率"与"损失"之间的关系
p_correct = np.linspace(0.01, 1.0, 100)
loss_values = -np.log(p_correct)

plt.figure(figsize=(8, 5))
plt.plot(p_correct, loss_values)
plt.title('Penalty for Prediction Confidence')
plt.xlabel('Predicted Probability for Correct Class')
plt.ylabel('Loss (-log(p))')
plt.grid(True, linestyle='--', alpha=0.7)
plt.hlines(y=-np.log(0.5), xmin=0, xmax=0.5, colors='r', linestyles='dashed')
plt.vlines(x=0.5, ymin=0, ymax=-np.log(0.5), colors='r', linestyles='dashed')
plt.text(0.51, 0.2, 'p=0.5, Loss=0.69', color='r')
plt.show()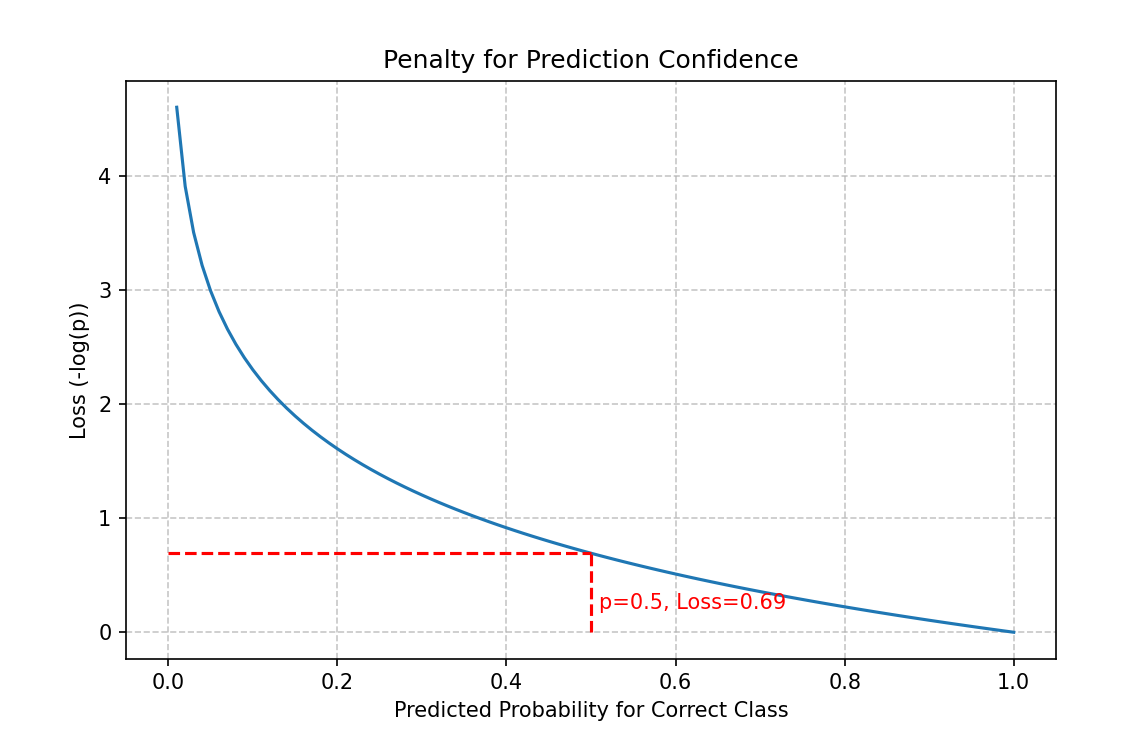

关键点 ：交叉熵对低置信度的正确预测惩罚极大（曲线左侧陡峭）。模型必须不仅猜对，而且要有信心地猜对。

2. 均方误差损失 (MSE Loss)：回归任务的"尺规"

核心思想 ：衡量模型预测的连续值 与真实值之间的平方距离 的平均值。它源于最大似然估计的思想，假设误差服从高斯分布。

直观比喻 ：打靶。预测值是子弹落点，真实值是靶心。MSE计算的是所有子弹落点到靶心距离的平方的平均值。距离越远，平方会放大这个误差，使得模型必须优先修正那些"离谱"的预测。

公式：
L=1n∑i=1n(yi−y^i)2L = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2L=n1∑i=1n(yi−y^i)2

代码与理论解释：

python 复制代码

import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
# 模拟预测房价 (单位: 万)
true_prices = torch.tensor([300., 450., 200.])
pred_prices = torch.tensor([320., 430., 180.])

# 计算MSE
mse_loss = nn.MSELoss()
loss_mse = mse_loss(pred_prices, true_prices)

# 计算MAE (L1 Loss) 作为对比
mae_loss = nn.L1Loss()
loss_mae = mae_loss(pred_prices, true_prices)

print(f"MSE Loss: {loss_mse.item():.2f}")
print(f"MAE Loss: {loss_mae.item():.2f}")

# 理论解释：为什么是平方？
# MSE的导数： dL/dy_pred = 2*(y_pred - y_true)
# 梯度与误差成正比，误差越大，更新步长越大，修正得越快。
errors = pred_prices - true_prices
gradients = 2 * errors
print(f"Errors: {errors}")
print(f"MSE Gradients: {gradients}") # 可以看到第三个误差最大，其梯度也最大

图表与对比：

python 复制代码

error = np.linspace(-3, 3, 100)
mse = error ** 2
mae = np.abs(error)

plt.figure(figsize=(8, 5))
plt.plot(error, mse, label='MSE Loss', lw=2)
plt.plot(error, mae, label='MAE Loss', lw=2)
plt.title('MSE vs. MAE')
plt.xlabel('Error (y_true - y_pred)')
plt.ylabel('Loss')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()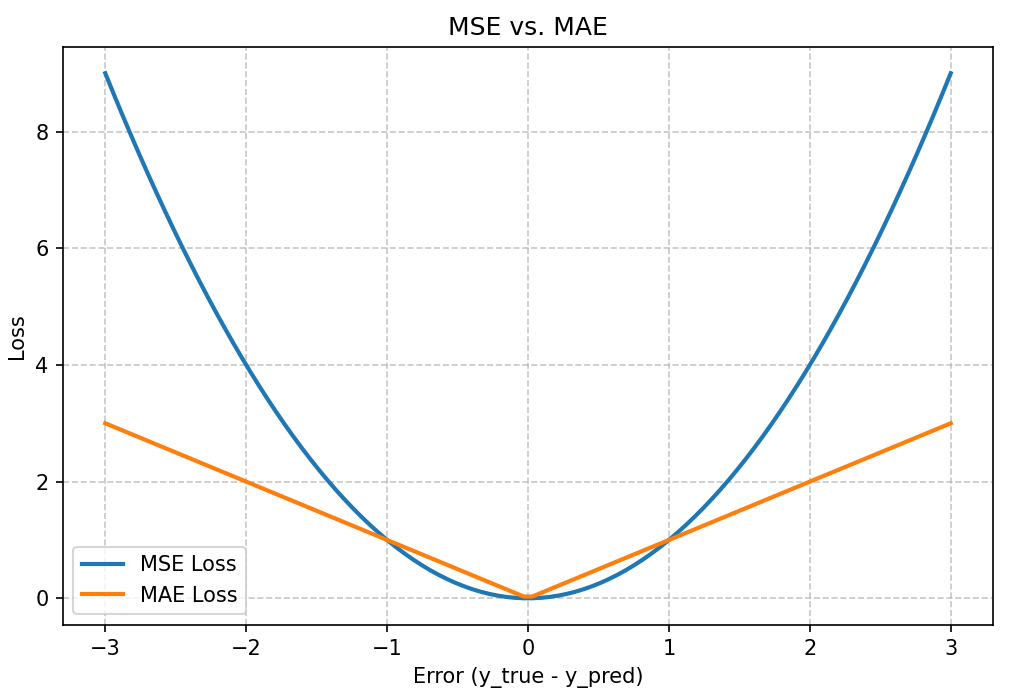

关键点：MSE对大误差（离群点）的惩罚远大于MAE。这使得模型训练时会更努力地修正大的错误，但对数据中的异常值也会非常敏感。

3. 对比学习损失 (InfoNCE Loss)：构建理解世界的"坐标系"

核心思想 ：在特征空间中，拉近相似样本（正样本对） ，推远不相似样本（负样本对） 。它是一种自监督学习的核心技术，能从未标注的数据中学习强大的特征表示。

正样本对：同一事物的不同视角（如一张图片的两次随机裁剪、同一段文本的两种释义）。
负样本对：批量中所有其他样本。

直观比喻：教一个AI认识人脸。

你给它看同一个人在不同光线、角度的照片（正样本对），告诉它"这些是同一个人"。
你给它看其他人的照片（负样本对），告诉它"这些是不同的人"。
InfoNCE就是衡量AI是否成功做到了这一点：它是否能把同一个人的各种照片在特征空间里拉得很近，同时把不同人的照片推得很远。

公式（InfoNCE） ：
Lq=−log⁡exp⁡(sim(q,k+)/τ)∑i=0Kexp⁡(sim(q,ki)/τ)L_q = -\log \frac{\exp(\text{sim}(q, k_+) / \tau)}{\sum_{i=0}^{K} \exp(\text{sim}(q, k_i) / \tau)}Lq=−log∑i=0Kexp(sim(q,ki)/τ)exp(sim(q,k+)/τ)

q: 查询样本的特征。
k+: 正样本的特征。
k_i: 负样本的特征。
sim(): 相似度函数，常用余弦相似度。
τ: 温度系数，控制对困难负样本的敏感度。

代码与实现（SimCLR风格）：

python 复制代码

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as np


def contrastive_loss(features, temp=0.1):
    """
    Standard implementation of InfoNCE loss (NT-Xent).
    Features are ordered as [aug1_batch, aug2_batch].
    """
    device = features.device
    batch_size = features.shape[0] // 2  # 原始批量大小

    # 正确构建labels: 对于每个样本，其正样本是它在另一组中的对应样本
    # 第i个样本的正样本是第i+batch_size个样本，反之亦然
    labels = torch.cat([torch.arange(batch_size) + batch_size, torch.arange(batch_size)]).to(device)

    # 计算余弦相似度矩阵
    features = F.normalize(features, dim=1)  # 归一化，使余弦相似度=点积
    similarity_matrix = torch.matmul(features, features.T)  # (2N, 2N)

    # 构建掩码，以排除自身（即q和k相同）的情况
    mask = torch.eye(2 * batch_size, dtype=torch.bool, device=device)

    # 提取正样本对的相似度分数
    # 正样本在对角线偏移batch_size的位置
    positives = torch.cat([
        similarity_matrix[range(batch_size), range(batch_size, 2 * batch_size)],
        similarity_matrix[range(batch_size, 2 * batch_size), range(batch_size)]
    ])

    # 提取负样本对的相似度分数
    # 将对角线元素设为一个大的负数，这样在softmax中它们的贡献接近0
    similarity_matrix = similarity_matrix.clone()
    similarity_matrix[mask] = -float('inf')
    negatives = similarity_matrix

    # 计算Logits和损失
    # 对于每个样本，分子是与正样本的相似度，分母是与所有样本的相似度
    logits = torch.cat([positives.unsqueeze(1), negatives], dim=1) / temp

    # 真实标签：正样本在位置0
    labels_ce = torch.zeros(2 * batch_size, dtype=torch.long, device=device)

    loss = F.cross_entropy(logits, labels_ce)
    return loss

图表与可视化：

python 复制代码

# 模拟特征
batch_size = 4
feat_dim = 2
features = torch.randn(2 * batch_size, feat_dim)
# 让正样本对特征相似
features[batch_size:] = features[:batch_size] + 0.1 * torch.randn(batch_size, feat_dim)

loss_nce = contrastive_loss(features, temp=0.1)
print(f"InfoNCE Loss: {loss_nce.item():.4f}")

plt.figure(figsize=(12, 5))

# 1. 学习前的特征空间
plt.subplot(1, 2, 1)
plt.scatter(features[:batch_size, 0].detach().numpy(), features[:batch_size, 1].detach().numpy(), c='blue',
            label='Augmentation 1')
plt.scatter(features[batch_size:, 0].detach().numpy(), features[batch_size:, 1].detach().numpy(), c='red', marker='x',
            label='Augmentation 2')
for i in range(batch_size):
    plt.plot([features[i, 0], features[i + batch_size, 0]], [features[i, 1], features[i + batch_size, 1]], 'k--',
             alpha=0.3)
plt.title("Feature Space Before Contrastive Learning")
plt.legend()

# 2. 模拟学习后的特征空间（正样本对聚拢，不同组分离）
plt.subplot(1, 2, 2)
# 假设经过学习，正样本对的特征几乎一致
features_learned = features.clone()
features_learned[batch_size:] = features_learned[:batch_size] + 0.01 * torch.randn(batch_size, feat_dim)
# 同时将不同组的数据点分开
features_learned[:batch_size] += torch.tensor([[1., 1.], [2., 2.], [3., 3.], [4., 4.]])
features_learned[batch_size:] += torch.tensor([[1., 1.], [2., 2.], [3., 3.], [4., 4.]])

plt.scatter(features_learned[:batch_size, 0].detach().numpy(), features_learned[:batch_size, 1].detach().numpy(),
            c='blue', label='Augmentation 1')
plt.scatter(features_learned[batch_size:, 0].detach().numpy(), features_learned[batch_size:, 1].detach().numpy(),
            c='red', marker='x', label='Augmentation 2')
for i in range(batch_size):
    plt.plot([features_learned[i, 0], features_learned[i + batch_size, 0]],
             [features_learned[i, 1], features_learned[i + batch_size, 1]], 'k--', alpha=0.3)
plt.title("Feature Space After Contrastive Learning")
plt.legend()
plt.tight_layout()
plt.show()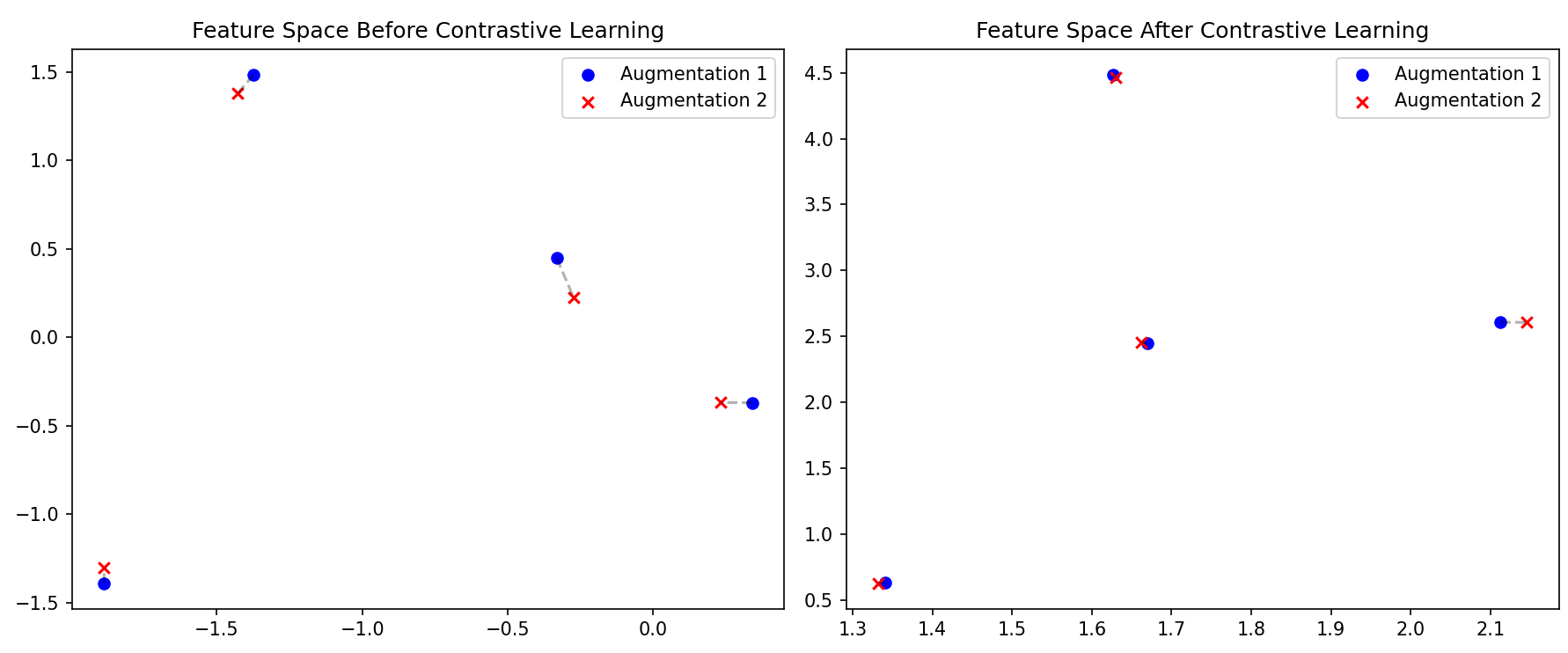

关键点 ：InfoNCE的强大之处在于它无需人工标注，通过自己构造正负样本，就能学习到一个结构化的特征空间，其中语义相似的样本会自动聚集在一起。

总结与对比

损失函数	核心任务	输入类型	核心思想	典型应用
交叉熵 (CE)	分类	概率分布	最小化预测分布与真实分布的差异	图像分类、情感分析、机器翻译
均方误差 (MSE)	回归	连续值	最小化预测值与真实值的平方距离	房价预测、气温预测、年龄估计
对比损失 (InfoNCE)	表征学习	特征向量	拉近正样本，推远负样本，学习结构化特征空间	自监督学习、图像检索、文本相似度计算

希望这个融合了代码实践、理论深度和直观解释的回答，能让你对这三种损失函数有一个全面而深刻的理解！好的，如果让我重新回答这个问题，我会整合之前的优点并针对不足之处进行完善，目标是打造一个更清晰、更严谨、更深入 ，同时保持直观易懂的回答。