电机控制(一)-电机分类

电机分类

电机分类：

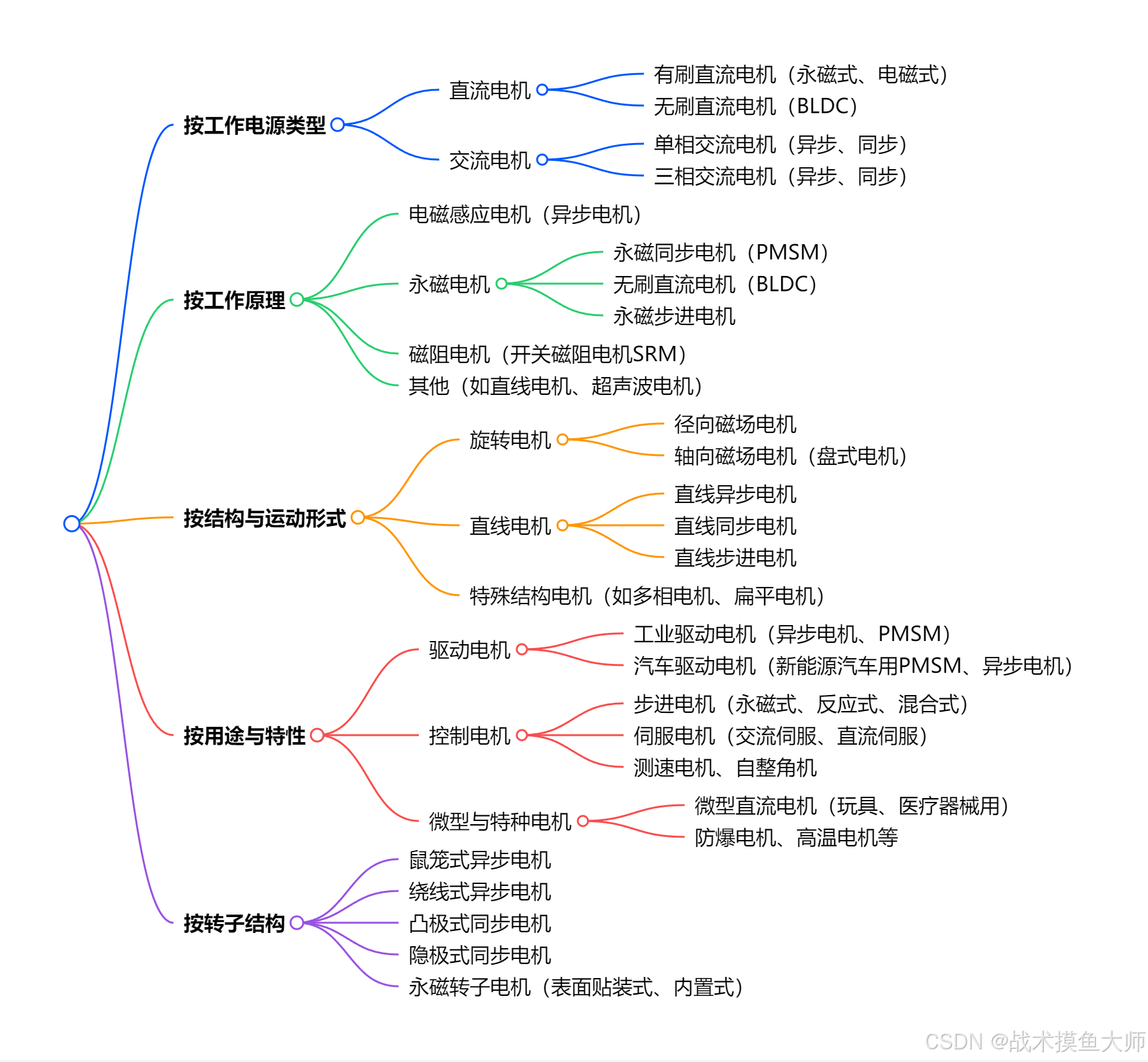
电机的拓扑模型并没有发生太大变化,变化较大的是控制电机的方法。

常见的电机类型有：

步进电机vs伺服电机

在工业自动化、机器人、精密设备等领域，步进电机和伺服电机是两种最常用的驱动电机，但两者的核心原理、性能定位、控制逻辑存在本质区别，选择时需结合精度、动态响应、成本等需求综合判断。下面从"核心区别"和"控制方式区别"两方面详细拆解：

核心区别（本质差异）

步进电机和伺服电机的根本差异源于"是否依赖反馈"------步进电机是开环控制的"位置执行器" ，伺服电机是闭环控制的"高精度驱动系统"，具体可通过下表对比：

对比维度	步进电机（Stepper Motor）	伺服电机（Servo Motor）
控制逻辑基础	开环控制（无位置/速度反馈）	闭环控制（必须搭配编码器等反馈元件）
运动原理	按"脉冲数"转动：每接收1个脉冲，电机转动固定角度（如1.8°/脉冲），脉冲数决定总转角，脉冲频率决定转速	按"指令目标"动态调节：通过反馈元件实时对比"指令值"与"实际值"，修正偏差，确保实际运动与指令一致
精度特性	1. 依赖"步距角精度"（如±5%），无反馈修正； 2. 存在"失步"风险（负载超过最大静力矩时，脉冲发了但电机没转，且无法察觉）； 3. 低速易"丢步"，高速易"过冲"	1. 精度由"反馈元件分辨率"决定（如编码器131072线/圈，精度远高于步进）； 2. 闭环修正偏差，无失步风险（负载超限时会报警或降速，而非丢步）； 3. 动态精度高，低速平稳、高速无过冲
动态响应	响应慢：加速/减速需缓慢（否则易失步），无法快速跟踪突变指令	响应快：闭环调节可快速修正偏差，能跟踪高频、突变的位置/速度指令（如机器人关节快速启停）
负载能力	1. 输出力矩随转速升高而下降（高速时力矩衰减明显）； 2. 过载能力差（短期过载即失步）	1. 输出力矩稳定（额定转速内力矩基本不变）； 2. 过载能力强（通常可承受2~3倍额定力矩，用于短期负载峰值）
成本与复杂度	成本低：电机+驱动器结构简单，无需反馈元件； 调试简单（只需设置细分、电流等基础参数）	成本高：电机+驱动器+编码器（反馈元件），系统复杂度高； 调试复杂（需整定PID、带宽等闭环参数）
典型应用场景	精度要求低、无动态跟踪需求的场景： ------ 3D打印机、小型数控机床（低端）； ------ 流水线传送带、阀门控制； ------ 小型自动化设备的固定位移驱动	高精度、高动态响应需求的场景： ------ 工业机器人关节、高端数控机床； ------ 半导体设备（晶圆搬运）、激光切割； ------ 精密检测仪器（如坐标测量机）

一般步进电机都是专用的步进电机，伺服电机是一整个伺服系统，指令 --- 反馈 --- 修正" 闭环，包括：伺服驱动器，电机本体，编码器。电机一般常选用永磁同步电机PMSM （或者叫交流无刷电机）或无刷直流电机BLDC 或异步感应电机IM

控制方式区别（从"开环"到"闭环"的逻辑差异）

两者的控制方式差异直接源于"是否有反馈"，具体可拆解为"控制信号类型""调节逻辑""故障处理"三个层面：

1. 步进电机的控制方式（开环控制）

步进电机的控制核心是"脉冲指令直接驱动 "，无需反馈，相当于"给多少脉冲，就按固定步距转多少"，控制逻辑简单直接。

如图为正点原子的一款步进电机，没有反馈单元，也没有反馈控制。

（1）核心控制组件

• 控制器：负责输出"脉冲信号"和"方向信号"（如PLC、单片机、运动控制卡）；
• 步进驱动器：接收控制器的脉冲/方向信号，将其转换为电机绕组的驱动电流（如细分驱动、恒流驱动），控制电机转动；
• 电机：无反馈元件，仅通过绕组通电顺序（如两相四拍、两相八拍）实现步进转动。

（2）控制逻辑流程

1. 控制器根据"目标位置"计算所需的"脉冲总数"（例：目标转角90°，电机步距角1.8°，则需脉冲数=90/1.8=500个）；
2. 控制器按"目标转速"输出对应频率的脉冲（例：转速60rpm，步距角1.8°，则每秒脉冲数=60×360/(60×1.8)=2000Hz），同时输出方向信号（正转/反转）；
3. 驱动器接收脉冲后，按"细分参数"（如16细分，将1.8°步距拆分为0.1125°/脉冲）驱动电机绕组通电，电机按固定步距转动；
4. 无反馈环节：无论电机是否实际转动（如负载过大导致失步），控制器都不会察觉，也不会修正------这是开环控制的最大局限。

（3）关键控制参数

• 细分：驱动器将电机固有步距角拆分（如16细分），用于提升精度（减小步距）和降低低速振动；
• 额定电流：根据电机参数设置驱动器输出电流，匹配电机力矩；
• 加减速曲线：为避免启动/停止时失步，需设置缓慢的加减速（如S型曲线），限制脉冲频率的突变速度。

2. 伺服电机的控制方式（闭环控制）

伺服电机的控制核心是"反馈修正偏差 "，相当于"先设定目标，再通过反馈实时对比实际值，修正控制量直到偏差为0"，控制逻辑更复杂但精度更高。

如图是rm比赛中的一款常见直流无刷伺服电机6020，可以看到伺服电机不光有电机本身，还有尾部的编码器，编码器根据原理又分为磁编码，光电编码。驱动器也集成在了电机中。

（1）核心控制组件

• 控制器：输出"位置指令""速度指令"或"力矩指令"（如运动控制卡、PLC、伺服驱动器自带的位置模式）；
• 伺服驱动器：核心是"闭环调节器"（通常是三环PID：位置环→速度环→电流环），接收控制器指令和编码器反馈，计算并输出驱动电流；
• 电机+反馈元件：电机自带高精度编码器（如增量式编码器、绝对值编码器），实时反馈电机的实际位置、速度。

（2）控制逻辑流程（以最常用的"位置模式"为例）

1. 控制器输出"目标位置指令"（如10000个脉冲，对应编码器的分辨率）；
2. 伺服驱动器的位置环：对比"目标位置"与编码器反馈的"实际位置"，计算位置偏差；
3. 位置环将"位置偏差"转换为"速度指令"，传递给速度环；
4. 速度环：对比"目标速度"与编码器计算的"实际速度"（通过位置变化率得到），计算速度偏差，转换为"电流指令"，传递给电流环；
5. 电流环：对比"目标电流"与电机绕组的"实际电流"，输出PWM驱动信号，控制电机转动，修正位置/速度偏差；
6. 实时反馈修正：编码器每秒反馈数万次实际位置，驱动器持续重复"对比-修正"过程，直到位置偏差接近0（通常偏差可控制在1个编码器计数内）。

（3）关键控制参数与模式

• 控制模式 ：伺服电机支持三种核心模式，按需切换：
  • 位置模式：按位置指令（脉冲/模拟量）控制转角；
  • 速度模式：按速度指令（模拟量/通讯）控制转速；
  • 力矩模式：按力矩指令（模拟量/通讯）控制输出力矩（如缠绕设备的恒张力控制）；
• PID参数整定：位置环、速度环、电流环的PID增益（比例、积分、微分）需调试，决定系统的动态响应（如响应速度、超调量）；
• 带宽 ：位置环/速度环的带宽（如位置环带宽1kHz），决定系统能跟踪的最高指令频率（带宽越高，动态响应越快）；
  • 带宽的含义：控制带宽通常以赫兹（Hz）为单位，表示系统增益（输出与输入之比）下降到低频增益的某个特定比例（如-3 dB点）时的频率值。在这个频率范围内，系统能较好地跟踪输入信号。
• 刚性：位置环增益的直观体现（刚性高，位置偏差小，但易震荡；刚性低，响应慢，但平稳）。

如何选择？

• 若需求是"低成本、低精度、无动态跟踪"（如固定位移、低速驱动），选步进电机（开环控制）；
• 若需求是"高精度、高动态、抗过载"（如快速启停、实时跟踪、精密定位），选伺服电机（闭环控制）。

简单来说：步进电机是"按指令'盲走'"，伺服电机是"按指令'看着走'，走偏了就修正"------这是两者最本质的区别。

步进电机也可以加装编码器，结合反馈组成伺服步进电机，可以避免大负载下的丢步现象。

直流无刷电机vs永磁同步电机vs异步无刷感应电机

直流无刷电机（BLDC）、永磁同步电机（PMSM）、异步无刷感应电机（无刷异步电机）是工业中最常用的三类无刷电机，三者的核心差异体现在磁路结构、电流波形、控制逻辑和性能特性上，适用场景也因此呈现明显分化。以下从"核心特性""性能参数""应用场景"三个维度进行全面对比：

核心特性对比（结构与原理差异）

三者的本质区别源于转子是否含永磁体 及电流/反电动势波形，这直接决定了它们的工作原理和控制方式：

特性维度	直流无刷电机（BLDC）	永磁同步电机（PMSM）	异步无刷感应电机（无刷异步电机）
转子结构	永磁体（如钕铁硼），表面贴装或内置	永磁体（高性能钕铁硼），多为内置式（提高凸极率）	无永磁体，铸铝鼠笼结构（靠感应电流产生磁场）
定子绕组	集中式绕组（绕组分布角度大，如120°）	分布式绕组（绕组分布角度小，如60°）	分布式绕组（与PMSM类似，但匝数和线径适配感应特性）
反电动势波形	梯形波（120°平顶段，三相互差120°电角度）	正弦波（平滑连续，三相互差120°电角度）	近似正弦波（由定子磁场感应产生，波形受转差率影响）
电流波形	方波/梯形波（与反电动势波形匹配，仅2相导通）	正弦波（与反电动势同相位，3相同时导通）	正弦波（由逆变器输出，需与定子磁场频率匹配）
换向方式	电子换向（基于霍尔传感器的"六步换相"）	电子换向（基于编码器的"矢量控制/FOC"）	无需换向（靠定子旋转磁场与转子感应电流作用）
同步性	准同步（转速≈电源频率×60/极对数，无转差）	严格同步（转速=电源频率×60/极对数，无转差）	异步（转速＜电源频率×60/极对数，有转差率）

关键性能参数对比（决定场景适配性）

性能参数的差异是三者应用场景分化的核心原因，尤其在效率、扭矩、控制精度等关键指标上对比显著：

性能维度	直流无刷电机（BLDC）	永磁同步电机（PMSM）	异步无刷感应电机（无刷异步电机）
效率	中高（80%-95%，高速段效率下降明显）	高（85%-98%，全转速段效率平稳）	中低（75%-90%，低速段效率低，有转子铜损）
功率密度	中（2-5 kW/kg）	高（3-8 kW/kg，永磁体贡献高磁场密度）	低（1-3 kW/kg，需更大体积产生同等功率）
启动/低速扭矩	较大（额定扭矩的2-3倍，梯形波电流特性）	大（额定扭矩的3-5倍，正弦波电流+高凸极率）	小（额定扭矩的1-2倍，依赖感应电流，启动慢）
控制精度	中等（步距角精度±5%，速度波动±2%）	高（位置精度±0.01°，速度波动±0.1%）	低（速度波动±5%，无位置闭环能力）
动态响应	中（响应时间10-50 ms）	快（响应时间1-10 ms，矢量控制带宽高）	慢（响应时间50-200 ms，转差率导致延迟）
成本	中（永磁体成本占比20%-30%，霍尔传感器廉价）	高（永磁体成本占比30%-50%，需高精度编码器）	低（无永磁体，转子结构简单，成本比BLDC低20%）
环境适应性	中等（永磁体耐温≤120℃，振动易导致磁性能衰减）	中等（永磁体耐温≤150℃，高温易退磁）	强（无永磁体，耐温可达180℃，抗振/抗粉尘）
维护需求	低（无电刷，仅需定期检查轴承）	中（编码器需定期校准，永磁体需避免强磁场干扰）	低（全封闭结构，几乎免维护）

典型应用场景对比（性能决定场景）

三者的应用场景严格匹配其性能特性，形成"高端精密选PMSM，中端通用选BLDC，低成本/恶劣环境选异步无刷"的格局：

应用领域	直流无刷电机（BLDC）典型场景	永磁同步电机（PMSM）典型场景	异步无刷感应电机典型场景
工业驱动	小型传送带、包装机械、呼吸机泵（中速、低成本）	数控机床主轴、机械臂关节、伺服压机（高精度、高动态）	大型风机、水泵、破碎机（低速、高负载、低成本）
汽车领域	车窗电机、座椅调节电机（低功率、低成本）	新能源汽车驱动电机、EPS转向电机（高功率密度、高续航）	空调压缩机、散热风扇（高温环境、低维护）
家电与消费电子	扫地机器人、无人机、变频洗衣机（中等精度、低噪音）	高端变频空调、空气净化器（高效率、低振动）	定频风扇、排油烟机（低成本、简单调速）
特种场景	医疗输液泵、小型无人机（中等可靠性、轻量）	航空航天伺服机构、半导体设备（高精度、高稳定性）	矿山机械、冶金风机（高温、高振动、粉尘环境）

核心区别总结与选型建议

1. 核心区别一句话概括：

   • BLDC："梯形波驱动的永磁无刷电机"，平衡成本与性能，适合中端通用场景；
   • PMSM："正弦波驱动的高精度永磁同步电机"，追求高性能，适合高端精密场景；
   • 异步无刷电机："无永磁体的感应电机"，以低成本和高可靠性取胜，适合恶劣环境与简单负载。

2. 选型优先级：

   • 若需高精度、高动态、高效率（如伺服系统、新能源汽车），选PMSM；
   • 若需中等精度、低成本、通用驱动（如家电、小型设备），选BLDC；
   • 若需耐极端环境、低维护、低成本（如矿山、冶金设备），选异步无刷电机。

三者并非替代关系，而是根据场景需求形成互补，共同覆盖从低端到高端的无刷电机应用谱系。

电机数学模型

对于控制来说我们比较关心电机的数学模型而非物理或者结构区别。其中磁链方程和电气方程是电机数学模型的两个核心方程。

要理解电机的磁链方程 和电气方程，首先需要明确一个核心逻辑：电机是"电生磁、磁生电、磁受力"的能量转换装置，这两个方程分别描述了"电与磁的耦合关系"和"电与磁的动态平衡关系"，是电机数学模型的基石。

磁链方程：描述"电流如何产生磁链"

磁链方程的本质是量化电流与磁链的线性耦合关系，核心是"电感矩阵"------因为电机的多个绕组（如定子三相、转子三相、励磁绕组等）之间既存在"自感"（自身电流产生的磁场），也存在"互感"（其他绕组电流产生的磁场）。

基础概念

在讲方程前，先明确两个关键术语：

• 磁链（ψ，单位：韦伯·匝，Wb·t） ：绕组匝数（N）与穿过绕组的磁通（Φ）的乘积，即 ψ = NΦ。它反映了绕组"链合"的磁场强弱，是比磁通更贴合电机分析的物理量。
• 电感（L，单位：亨利，H） ：衡量电流产生磁链能力的参数，定义为 L = ψ / i（自感：自身电流产生的磁链与自身电流的比值；互感：其他绕组电流产生的磁链与该电流的比值，记为M）。

磁链方程的通用形式

电机的绕组可视为一个"电流向量"（各绕组电流的集合），磁链可视为"磁链向量"（各绕组磁链的集合），两者通过电感矩阵 线性关联，通用形式为：
ψ = L ⋅ i \boxed{\psi} = \boxed{L} \cdot \boxed{i} ψ=L⋅i

其中：

• ψ = [ ψ 1 , ψ 2 , . . . , ψ n ] T \boxed{\psi} = [\psi_1, \psi_2, ..., \psi_n]^T ψ=[ψ1,ψ2,...,ψn]T：n阶磁链列向量（n为绕组数量，如异步电机定转子共6个绕组，n=6）；
• i = [ i 1 , i 2 , . . . , i n ] T \boxed{i} = [i_1, i_2, ..., i_n]^T i=[i1,i2,...,in]T：n阶电流列向量；
• L \boxed{L} L：n×n阶电感矩阵，对角线元素为自感 （ L i i L_{ii} Lii，如定子A相自感 L A A L_{AA} LAA），非对角线元素为互感 （ L i j L_{ij} Lij，如定子A相与B相间的互感 L A B L_{AB} LAB）。

关键特性与示例（以异步电机为例）

异步电机是最典型的多绕组电机（定子三相绕组+转子三相绕组，共6个绕组），其磁链方程能直观体现电感矩阵的特点：

需要注意的是，三相绕组指的是输入的电流有三相，每一相实际可以对应多个物理绕组。理论上三相只需要六个槽，实际电机中远不止6槽，常见24槽。

可以参考这个视频

电感矩阵的结构

异步电机的电感矩阵 L 6 × 6 \boxed{L}{6×6} L6×6 可按"定子绕组"和"转子绕组"分块，形式如下：
L = [ L s L s r L r s L r ] \boxed{L} = \begin{bmatrix} \boxed{L}s & \boxed{L}{sr} \\ \boxed{L}{rs} & \boxed{L}_r \end{bmatrix} L=[LsLrsLsrLr]

• L s \boxed{L}s Ls（3×3）：定子绕组自互感矩阵，对角线为定子各相自感（ L s s L{ss} Lss，三相对称时相等），非对角线为定子相间互感（ L s m L_{sm} Lsm，如 L A B = L B C = L C A = − L s m L_{AB}=L_{BC}=L_{CA}=-L_{sm} LAB=LBC=LCA=−Lsm，负号因绕组空间相差120°，磁链方向相反）；
• L r \boxed{L}_r Lr（3×3）：转子绕组自互感矩阵，结构与 L s \boxed{L}_s Ls对称（转子三相也对称）；
• L s r \boxed{L}{sr} Lsr（3×3）、 L r s \boxed{L}{rs} Lrs（3×3）：定转子互感矩阵，满足 L s r = L r s T \boxed{L}{sr} = \boxed{L}{rs}^T Lsr=LrsT（互感可逆），且随转子位置变化（因为转子旋转会改变定转子绕组的空间相对位置，导致互感时变，这是异步电机方程"耦合、时变"的核心原因）。

异步电机磁链方程的展开

以定子A相（ ψ A \psi_A ψA）和转子a相（ ψ a \psi_a ψa）为例，展开后可直观看到电流对磁链的贡献：

• 定子A相磁链： ψ A = L s s i A + L s m i B + L s m i C + M s r cos ⁡ θ i a + M s r cos ⁡ ( θ + 120 ° ) i b + M s r cos ⁡ ( θ − 120 ° ) i c \psi_A = L_{ss}i_A + L_{sm}i_B + L_{sm}i_C + M_{sr}\cos\theta i_a + M_{sr}\cos(\theta+120°)i_b + M_{sr}\cos(\theta-120°)i_c ψA=LssiA+LsmiB+LsmiC+Msrcosθia+Msrcos(θ+120°)ib+Msrcos(θ−120°)ic
  （前三项是定子电流产生的磁链，后三项是转子电流产生的磁链， θ \theta θ为定转子空间夹角）；
• 转子a相磁链： ψ a = M s r cos ⁡ θ i A + M s r cos ⁡ ( θ − 120 ° ) i B + M s r cos ⁡ ( θ + 120 ° ) i C + L r r i a + L r m i b + L r m i c \psi_a = M_{sr}\cos\theta i_A + M_{sr}\cos(\theta-120°)i_B + M_{sr}\cos(\theta+120°)i_C + L_{rr}i_a + L_{rm}i_b + L_{rm}i_c ψa=MsrcosθiA+Msrcos(θ−120°)iB+Msrcos(θ+120°)iC+Lrria+Lrmib+Lrmic
  （前三项是定子电流产生的磁链，后三项是转子电流产生的磁链）。

实际应用中的关键简化

原始磁链方程因"时变互感"（如异步电机的 θ \theta θ变化）和"多绕组耦合"，求解复杂，工程中常用坐标变换（如dq0变换、αβ变换）简化：

• 变换后，定转子绕组的"时变互感"变为"恒定互感"，"三相耦合"变为"dq轴解耦"；
• 简化后的磁链方程（如dq轴下）： ψ d = L d i d \psi_d = L_d i_d ψd=Ldid， ψ q = L q i q \psi_q = L_q i_q ψq=Lqiq（同步电机），或 ψ s = L s i s + L m i r \psi_s = L_s i_s + L_m i_r ψs=Lsis+Lmir， ψ r = L m i s + L r i r \psi_r = L_m i_s + L_r i_r ψr=Lmis+Lrir（异步电机矢量控制模型），大幅降低控制难度。

在电机控制中需要用到矢量变换，对于三相电机，主要有三个坐标系

坐标系统：三相静止（abc）坐标，两相静止（αβ）坐标、两相旋转（dq0）坐标

变换方法：Clarke 变换、Park 变换是 "从原始坐标系到目标坐标系的数学工具"。

Clarke 变换实现 "三相静止→两相静止（αβ）"，Park 变换实现 "两相静止（αβ）→两相旋转（dq）"，两者结合可完成 "三相静止（abc）→两相旋转（dq0）" 的完整变换。
这部分后续还会再提到。

影响磁链方程的核心因素

• 气隙长度：气隙越大，磁阻越大，自感和互感越小（电感与磁阻成反比）；
• 铁芯饱和：上述方程默认"线性电感"（铁芯不饱和），实际中铁芯饱和会导致电感随电流增大而减小，需引入"非线性电感模型"修正；
• 绕组结构：绕组匝数越多、导线越粗，自感越大；绕组空间夹角越小，互感越大。

电气方程：描述"电压与磁链、电流的动态平衡"

电气方程的本质是基尔霍夫电压定律（KVL）在电机绕组中的延伸，核心是"电压 = 电阻压降 + 感应电动势"------但电机的感应电动势分为两类，需特别注意。

核心物理量：两类感应电动势

电机绕组中的感应电动势并非只有"变压器电动势"，还有"运动电动势"，两者的区别是理解电气方程的关键：

• 变压器电动势（ e t = − d ψ d t e_t = -\frac{d\psi}{dt} et=−dtdψ） ：磁链随时间变化产生的电动势（如变压器副边感应电动势），与绕组是否旋转无关，仅由 ψ \psi ψ的变化率决定，符号由楞次定律（阻碍磁链变化）确定；
• 运动电动势（ e v = ω × ψ e_v = \omega \times \psi ev=ω×ψ）：绕组在磁场中旋转（或磁场相对绕组运动），导体切割磁感线产生的电动势（如发电机的感应电动势），与"磁链大小"和"旋转角速度（ω）"成正比，方向由右手定则确定。

在电机绕组中，感应电动势的产生本质是导体切割磁感线或磁通量穿过绕组发生变化（法拉第电磁感应定律），但根据磁场来源和绕组运动关系的不同，核心可分为旋转电动势（动生电动势） 和变压器电动势（感生电动势） 两类。

旋转电动势的核心是绕组导体与磁场发生相对运动，导体切割磁感线产生的电动势，因常见于转子绕组旋转切割定子磁场的场景（如直流电机、异步电机转子），故得名 "旋转电动势"；从电磁感应本质看，属于法拉第定律中的 "动生电动势"（由导体运动导致磁通量变化）。

变压器电动势的核心是绕组导体静止，但穿过绕组的磁通量随时间变化（如交变磁场），导致绕组中产生的电动势，因与变压器原副边绕组的感应机制完全一致，故得名 "变压器电动势"；从电磁感应本质看，属于法拉第定律中的 "感生电动势"（由磁场变化导致磁通量变化，与导体运动无关）。

电气方程的通用形式

对于任意一个电机绕组，其端电压（u）满足：
u = R i + e t + e v u = R i + e_t + e_v u=Ri+et+ev

代入两类电动势的表达式，展开为：
u = R i + d ψ d t + ω × ψ u = R i + \frac{d\psi}{dt} + \omega \times \psi u=Ri+dtdψ+ω×ψ

（注：若绕组静止，如定子绕组，运动电动势 e v = 0 e_v=0 ev=0，方程简化为 u = R i + d ψ d t u = R i + \frac{d\psi}{dt} u=Ri+dtdψ；若磁链恒定，如直流电机稳态，变压器电动势 e t = 0 e_t=0 et=0，方程简化为 u = R i + e v u = R i + e_v u=Ri+ev）。

关键示例（以同步电机dq轴为例）

同步电机的转子有励磁绕组，且以同步角速度（ω₁）旋转，工程中常用"dq0坐标变换"将三相绕组等效为"d轴（直轴，与励磁磁场同向）"和"q轴（交轴，与励磁磁场垂直）"的两相绕组，其电气方程最具代表性：

电机中存在两个主要磁场：励磁磁场、电枢磁场。其中励磁磁场为主磁场，建立 "稳定的、用于能量转换的基础磁场"。电枢磁场与励磁磁场相互作用，产生电磁转矩（电动机）或感应电动势（发电机）。

电机运行过程中，电枢磁场会对励磁磁场（主磁场）产生影响，这种影响称为电枢反应，为了抵消电枢反应的负面影响，电机设计中会采取专门措施：如直流电机在定子上增加 "补偿绕组"（抵消电枢磁场），同步电机在转子上设置 "阻尼绕组"（抑制磁场畸变）。

d轴电气方程（定子d轴绕组）

u d = R s i d + d ψ d d t − ω 1 ψ q u_d = R_s i_d + \frac{d\psi_d}{dt} - \omega_1 \psi_q ud=Rsid+dtdψd−ω1ψq

• u d u_d ud：定子d轴端电压； R s R_s Rs：定子电阻； i d i_d id：d轴电流； ψ d \psi_d ψd：d轴磁链；
• 关键项： − ω 1 ψ q -\omega_1 \psi_q −ω1ψq是d轴的运动电动势（因q轴磁链在d轴绕组中旋转产生，负号由dq轴正交关系决定）。

q轴电气方程（定子q轴绕组）

u q = R s i q + d ψ q d t + ω 1 ψ d u_q = R_s i_q + \frac{d\psi_q}{dt} + \omega_1 \psi_d uq=Rsiq+dtdψq+ω1ψd

• 关键项： + ω 1 ψ d +\omega_1 \psi_d +ω1ψd是q轴的运动电动势（d轴磁链在q轴绕组中旋转产生，方向与d轴相反）。

励磁绕组电气方程（转子励磁绕组，静止于d轴）

u f = R f i f + d ψ f d t u_f = R_f i_f + \frac{d\psi_f}{dt} uf=Rfif+dtdψf

• 励磁绕组随转子旋转，但始终与d轴同向，无运动电动势（ e v = 0 e_v=0 ev=0）；
• ψ f = L f i f + L f d i d \psi_f = L_f i_f + L_{fd} i_d ψf=Lfif+Lfdid（励磁磁链由励磁电流 i f i_f if和定子d轴电流 i d i_d id共同产生， L f L_f Lf为励磁自感， L f d L_{fd} Lfd为定转子d轴互感）。

电气方程与磁链方程的关联

电气方程中的 ψ \psi ψ（磁链）需通过磁链方程 计算（ ψ = L i \psi = L i ψ=Li），因此两个方程是"嵌套关系"：

1. 由电流 i \boxed{i} i通过磁链方程得到 ψ \boxed{\psi} ψ；
2. 将 ψ \boxed{\psi} ψ代入电气方程，得到电压 u \boxed{u} u与电流 i \boxed{i} i的动态关系。

这种关联是电机"电压-电流-磁链"动态特性的完整描述，也是电机仿真（如MATLAB/Simulink）和控制系统设计（如矢量控制、直接转矩控制）的核心依据。

两个方程的核心应用场景

理解磁链方程和电气方程，本质是掌握电机的"数学语言"，其应用贯穿电机分析与控制的全流程：

1. 电机运行状态分析 ：如异步电机启动时的电流冲击（磁链方程中互感时变导致 d ψ d t \frac{d\psi}{dt} dtdψ增大，电气方程中电压不变则电流增大）；
2. 控制系统设计：如矢量控制的核心是"通过坐标变换，将时变的磁链/电气方程转化为解耦的直流电机模型"，实现对磁链和转矩的独立控制；
3. 故障诊断 ：如电机绕组短路时，自感减小，磁链方程中 ψ \psi ψ与 i i i的比值异常，可通过电气方程的电压电流偏差诊断故障。

总结

对比维度	磁链方程	电气方程
核心物理关系	电流 → 磁链（磁耦合）	电压 → 电流 + 磁链（能量平衡）
关键参数	自感、互感（电感矩阵）	电阻、磁链变化率、旋转角速度
核心电动势	无（仅描述磁链产生）	变压器电动势 + 运动电动势
工程简化手段	坐标变换（解耦时变互感）	结合磁链方程，将 ψ \psi ψ替换为 L i L i Li
本质作用	建立"电→磁"的定量关系	建立"电→磁→电"的动态平衡

简言之：磁链方程是"因"（电流产生磁链），电气方程是"果"（磁链变化产生电动势，与电压平衡），两者共同构成了电机能量转换的数学核心。