直接选择排序(排升序)
选择排序,就是从一组数据当中找到最小(最大)的数据,放在数据的起始位置。我们需要两个变量begin和mini,begin最一开始为数组的0下标,mini负责去数据里边寻找最小的那个数,放到begin的位置。之后,begin++,再次重复刚才的过程,直到begin越界,至此,整个数组变成升序的了。这种方式是可以完成任务的,但是需要便利整个数组,导致循环的次数增加,可以优化一下,我们再定义两个变量end和maxi,end一开始为数组的最后一个下标,maxi负责去找最大的那个数据,放到end的位置,每交换完一次end--,不断循环直至越界,结合上边寻找最小值的操作,整个数组只需要便利一半的数据就可以实现升序。
代码实现:(代码里边有些细节会在下边解释)
cpp
#include<stdio.h>
//打印数组
void Print(int* arr, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
//交换两个元素
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//直接选择排序
void SelectSort(int* arr, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
//maxi和mini在最一开始都指向begin的位置
int maxi = begin;
int mini = begin;
//每一次寻找最大最小值都是在begin + 1和end的范围之中
for (int i = begin + 1; i <= end; i++)
{
if (arr[i] > arr[maxi])
{
maxi = i;
}
if (arr[i] < arr[mini])
{
mini = i;
}
}
if (maxi == begin)
{
maxi = mini;
}
Swap(&arr[mini], &arr[begin]);
Swap(&arr[maxi], &arr[end]);
begin++;
end--;
}
}
int main()
{
int arr[] = { 5,3,9,6,2,4,7,1,8 };
int len = sizeof(arr) / sizeof(int);
SelectSort(arr, len);
Print(arr, len);
return 0;
}上边的排序是对539624718这组数据进行升序排序,按照我们之前的想法,利用maxi和mini去找最大值和最小值,然后分别和end,begin交换,不断循环直至begin == end 的时候,整个数组也就便利完了,也意味着整个数组已经有序了。
在代码中有几个细节,最一开始的maxi和mini不是指向下标为0,而是直接赋值begin,因为每找到一次最大最小值并且交换之后,begin的值就要++,我们每次都是会在begin~end这个范围区间去寻找最大最小值,而maxi和mini每次都是指向的区间的最起始的下标位置,那自然就是begin。
在内层循环之中,i从begin + 1的地方开始,起始也可以从begin的位置开始,但是由于maxi和mini在最一开始的时候就是在begin的位置,那如果i从begin的位置开始的话就会有一次比较是重复的。
找完了最大最小值后的if条件判断begin是否等于end(此类情况如下图所示)
此时maxi和mini已经来到了正确的位置,但如果现在直接交换,两次交换完之后就会变成
4 6 2,这显然不是我们想要的正确的顺序,这样的原因就是当最小值和begin交换完位置之后,maxi所在的位置就不是最大值了,最大值被交换到mini的位置了,为了解决,我们就先让maxi到mini的位置,这样交换完数据之后,最大值会到mini的位置,而此时maxi也在这个位置,就可以实现正确的排序。
直接选择排序的时间复杂度
直接选择排序的时间复杂度受到内外循环的双重影响,可以简单画个表格来理解。
外循环 begin end 内循环 i 循环最深语句的执行次数
0 n - 1 1 n - 1
1 n - 2 2 n - 3
. . . .
. . . .
(n / 2) - 1 n / 2 n / 2 1
对执行次数进行累加,最后再根据大0表示法的规则,得出结论,直接选择排序的时间复杂度为O(N^2)
堆排序
堆排序也是属于选择排序,根据堆的特点,最值一定是在堆顶的原理,相当于也是选择出来的。
堆排序就是利用堆这一个数据结构的思想,将一组数据建成一个堆结构,然后再进行出堆操作,由于最值是在堆顶,所以要想将数据排成升序的,要建大堆,因为如果是大堆,每次出堆的时候,数据中最大的元素就会出堆,以此类推,最终就会变成升序。(这里指的出堆并不是真的删除数据,数据还是在数组里边的)。
关于建堆,有两种方式,一种是向上调整建堆,一种是向下调整建堆。
以下都以数据 5,3,9,6,2,4,7,1,8 作为解释
**向下调整建堆:**我们将数据直接看作是一个堆,从最后一棵子树开始向下进行调整,若最后一棵子树的叶子节点的下标是i的话,根据公式可以知道它的父亲节点的下标为(i - 1) / 2。当这棵子树调整完了之后就调整它的前面一棵子树,直接i--就可以找到它的前边一颗子树,不断循环,直到i为无效下标。
**向上调整建堆:**我们将数据分开来看,如果只有一个数据5(也就是下标为0的位置)的话,那么它就是一个堆,不用调整,直接i++,当i的下标为1的时候,把它看做是一个孩子节点,通过向上调整算法将下标为0和下标为1的数据组成的一个树调整成真正的堆。按照这种思想,我们只需要便利一遍数组,每便利到一个数据,就把它当成孩子节点进行向上调整算法。
当我们终于将这组数据调整成堆结构之后,就可以开始所谓排序了,只需进行出堆操作,不段循环出堆操作,最终堆里边仅剩一个节点的时候,整个数据已经变成我们想要的升序了。
代码实现:
cpp
#include<stdio.h>
//打印数组
void Print(int* arr, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
//交换两个元素
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//向下调整算法
void AdjustDown(int* arr, int parent,int n)
{
int child = (parent * 2) + 1;
while (child < n)
{
//找最大孩子---如果右孩子存在并且比左孩子大,child++
if (child + 1 < n && arr[child + 1] > arr[child])
{
child++;
}
//最大孩子和根节点比较---孩子节点大就跟父亲节点交换
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = (parent * 2) + 1;
}
else
{
break;
}
}
}
//向上调整算法
void AdjustUp(int* arr,int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* arr, int n)
{
////向下调整建堆
//for (int i = (n - 1 - 1) / 2; i >= 0; i--)
//{
// AdjustDown(arr, i,n);
//}
//向上调整建堆
for (int i = 0; i < n; i++)
{
AdjustUp(arr, i);
}
while (n > 0)//如果堆里边只剩下一个元素就结束循环
{
Swap(&arr[0], &arr[n - 1]);
n--;
AdjustDown(arr, 0, n);
}
}
int main()
{
int arr[] = { 5,3,9,6,2,4,7,1,8 };
int len = sizeof(arr) / sizeof(int);
HeapSort(arr, len);
Print(arr, len);
return 0;
}堆排序的时间复杂度
由于堆也是属于完全二叉树,而满二叉树也是属于完全二叉树,在计算复杂度的时候多出来的节点或者少的节点不会特别影响到时间复杂度。所以我们在计算的时候将堆看作是一个完全二叉树就行。
向上调整建堆的时间复杂度(如下图)
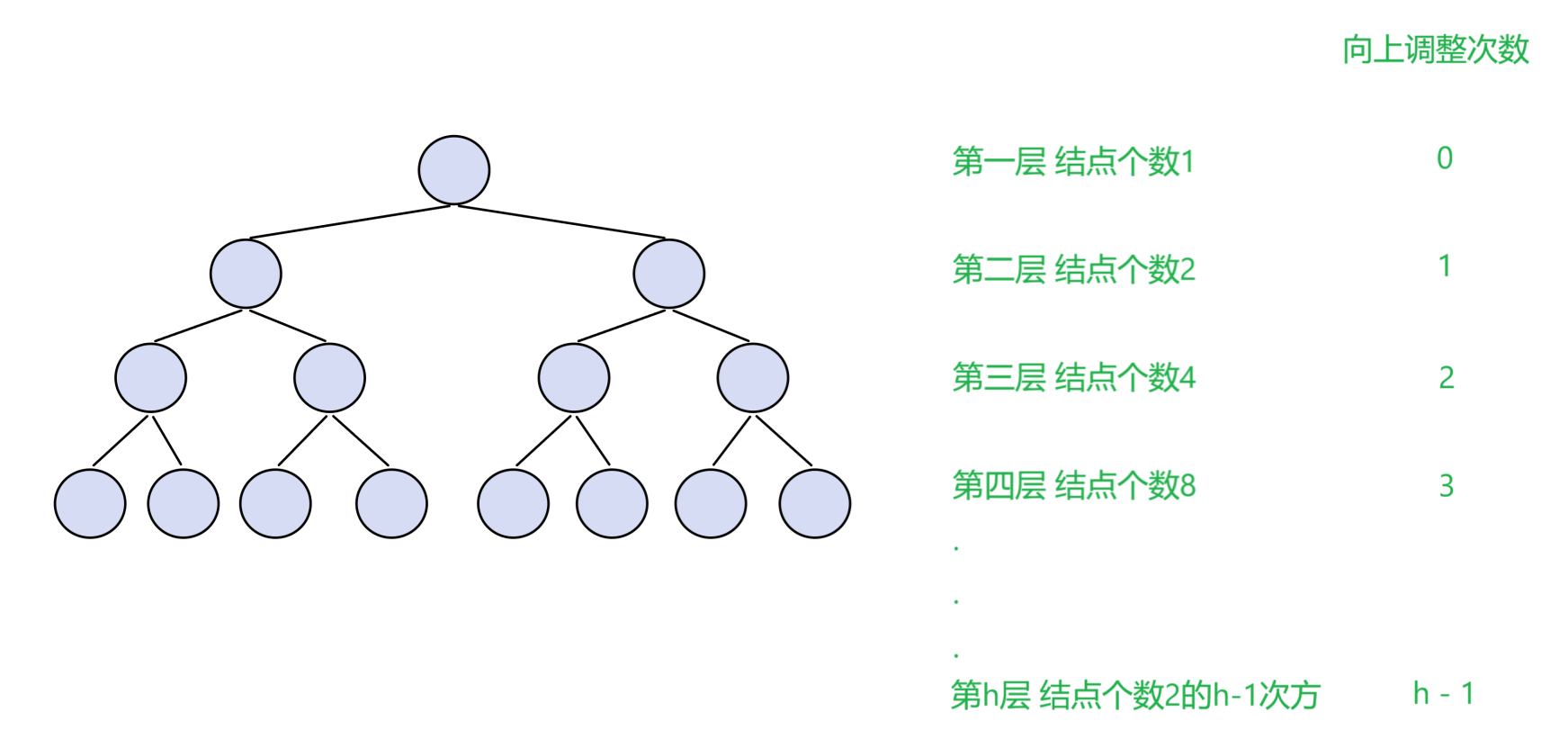
每一层的节点个数和每一个节点的调整次数都已经列出,接下来进行累加以及错位相减的相关计算就能得出最后的时间复杂度为O(N * logN)
向下调整建堆的时间复杂度(如下图)
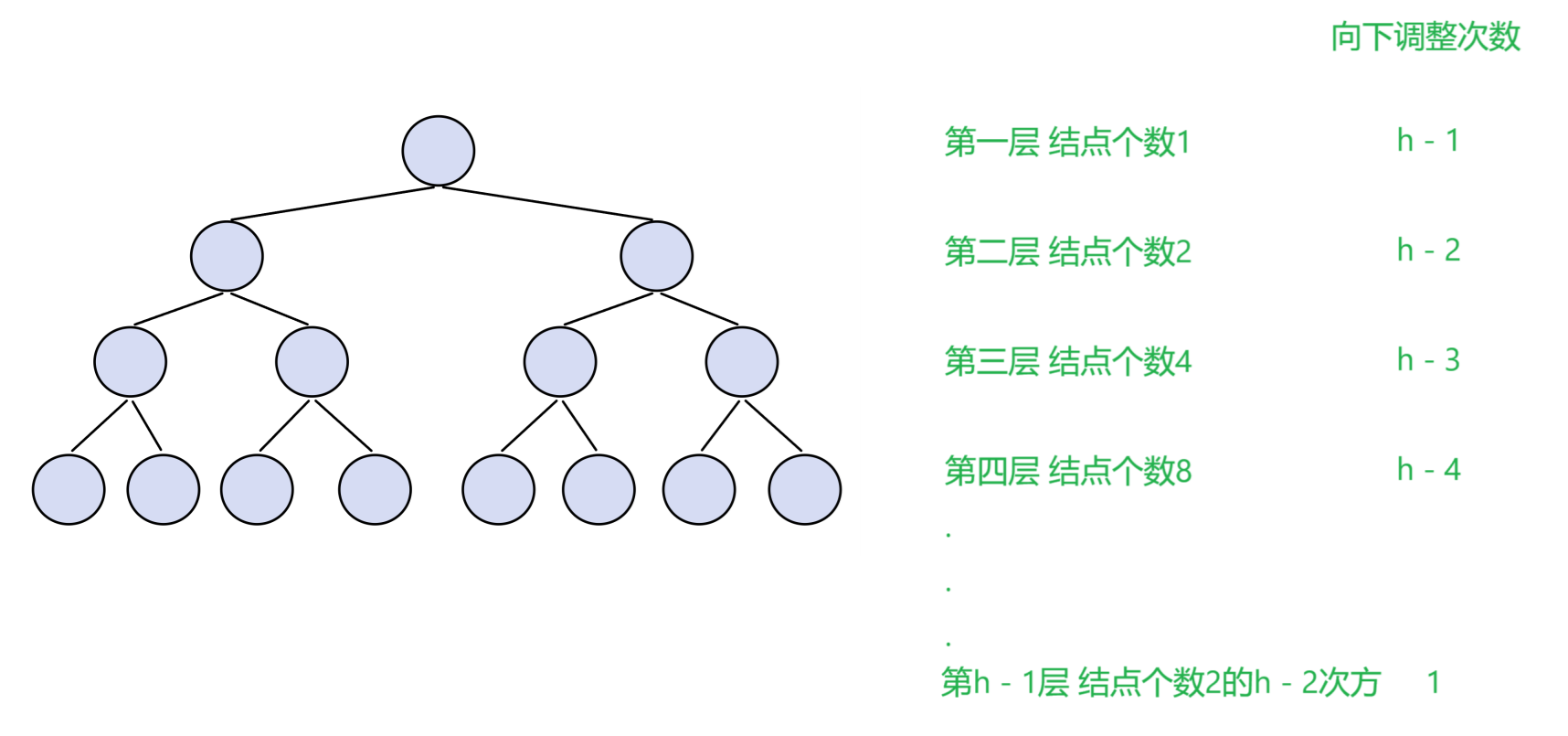
同理计算,总的执行次数等于每一层的结点个数乘向下调整次数的总和,最终算出来为O(N)
在堆排序里里边,除了向上(向下)调整建堆,还有真正的堆排序的代码,它的时间复杂度是
O(N*logN)
最终堆排序的时间复杂度就是O(N*logN)
