在线结构光系统中,所有的激光线中心点都遵守光平面的约束,即所有的激光线中心点都位于光平面上,并符合光平面方程。光平面的存在为待测物体上的标志点的深度信息的求解提供了约束。光平面方程的标定精度会直接影响系统重加精度。
光平面方程标
在空间中平面可以表示为如下形式:
L: aXc+bYc+cZc=d(1-1) L: \; aX_c + bY_c + cZ_c = d \tag{1-1} L:aXc+bYc+cZc=d(1-1)
其中(a, b, c)为平面法向量𝑛,d为平面到原点的偏移量。通常平面方程的求解步骤为:
- 提取激光线中心;
- 接着根据已知多组激光线点三维坐标点𝑃𝑖 = (𝑥𝑖, 𝑦𝑖, 𝑧𝑖),拟合激光平面的方程获得光平面参数。
激光条纹中心提取
(具体原理与代码另外介绍)
由于激光线中心点是进行光平面标定的直接数据,所以激光中心线提取作为光平面标定的第一步也是非常重要的一步,对光平面标定的精确性以及后续三维重建或拼接的准确性有着重要影响。虽然在标定时使用的激光线上的点是由一系列没有宽度的点连接而成的,但实际上线激光发生装置在对标定板或待测物体上投射线激光时,在标定板或待测物体上留下的激光线条纹是一条有宽度的的激光条。激光线条中间的亮度最高,越向周围延申则光强越弱,光条的亮度分布近似服从高斯分布,如图2- 3所示。
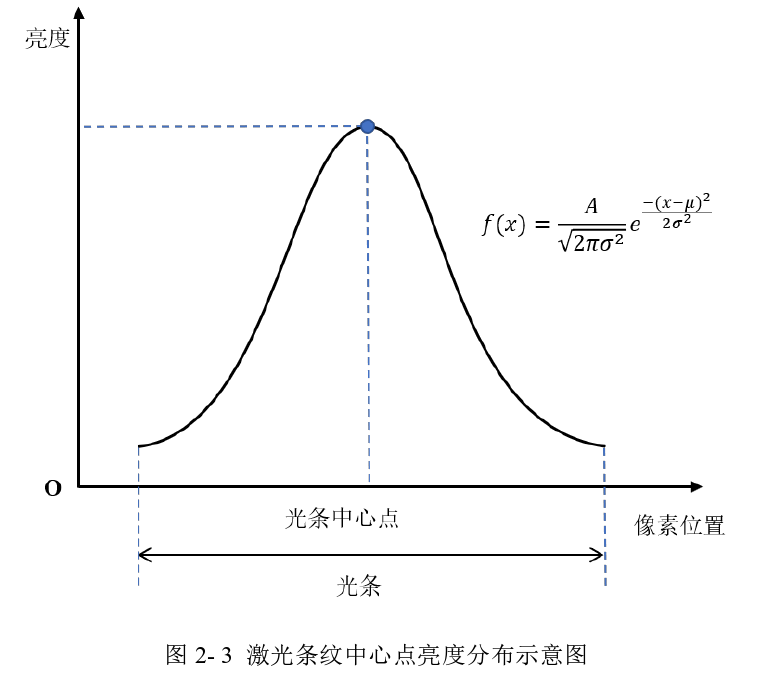
下面以Steger方法为例进行介绍。
steger算法根据Hessian矩阵可以计算出激光条纹的法向,然后根据法向进行泰勒式展开后可以得到亚像素坐标值.即Hessian矩阵特征值绝对值最大 的对应的特征向量就是光强变化最快的方向,可以沿着这个方向去寻找亮度最高的像素点即激光线中心点。
若图像中有一个像素点(x,y)(x,y)(x,y), 则该点的Hessian矩阵的表达式为:
H(x,y)=[IxxIxyIxyIyy](1-2) H(x,y) = \begin{bmatrix} I_{xx} & I_{xy} \\ I_{xy} & I_{yy} \end{bmatrix}\tag{1-2} H(x,y)=[IxxIxyIxyIyy](1-2)
其中,
以(𝑥0,𝑦0)(𝑥_0, 𝑦_0)(x0,y0)点为初始点,为法向量方向上的所有点都计算Hessian矩阵,设线中心点的坐标为(𝑝𝑥,𝑝𝑦)=(𝑥0+𝑡𝑛𝑥,𝑦0+𝑡𝑛𝑦)(𝑝_𝑥, 𝑝_𝑦) = (𝑥_0 + 𝑡𝑛_𝑥, 𝑦_0 + 𝑡_𝑛𝑦)(px,py)=(x0+tnx,y0+tny)并使上的亮度分布多项式
I=I(x0,y0)+t[nxny][IxIy]+t22![nxny][IxxIxyIxyIyy][nxny](1-3) I = I(x_0, y_0) + t \begin{bmatrix} n_x & n_y \end{bmatrix} \begin{bmatrix} I_x \\ I_y \end{bmatrix}+ \frac{t^2}{2!} \begin{bmatrix} n_x & n_y \end{bmatrix} \begin{bmatrix} I_{xx} & I_{xy} \\ I_{xy} & I_{yy} \end{bmatrix} \begin{bmatrix} n_x \\ n_y \end{bmatrix}\tag{1-3} I=I(x0,y0)+t[nxny][IxIy]+2!t2[nxny][IxxIxyIxyIyy][nxny](1-3)
其中I=I(x0,y0)I = I(x_0, y_0)I=I(x0,y0) 表示当前图像亮度。[IxIy]\begin{bmatrix}I_x \\I_y\end{bmatrix}[IxIy] 表示一阶导数, [IxxIxyIxyIyy]\begin{bmatrix} I_{xx} & I_{xy} \\ I_{xy} & I_{yy} \end{bmatrix}[IxxIxyIxyIyy] 表示二阶导数。将此多项式对t求导,等于0的地方即为亮度最高的像素值坐标,即激光线中心点,如式所示
∂I∂t=[nxny][IxIy]+t[nxny][IxxIxyIxyIyy][nxny]=0(1-4) \frac{\partial I}{\partial t} = \begin{bmatrix} n_x & n_y \end{bmatrix} \begin{bmatrix} I_x \\ I_y \end{bmatrix}+ t \begin{bmatrix} n_x & n_y \end{bmatrix} \begin{bmatrix} I_{xx} & I_{xy} \\ I_{xy} & I_{yy} \end{bmatrix} \begin{bmatrix} n_x \\ n_y \end{bmatrix} = 0\tag{1-4} ∂t∂I=[nxny][IxIy]+t[nxny][IxxIxyIxyIyy][nxny]=0(1-4)
由公式1-4可得
t=−nxIx+nyIynx2Ixx+2nxnyIxy+ny2Iyy t = - \frac{n_x I_x + n_y I_y}{n_x^2 I_{xx} + 2n_x n_y I_{xy} + n_y^2 I_{yy}} t=−nx2Ixx+2nxnyIxy+ny2IyynxIx+nyIy
由于泰勒展开只在很小的范围内适用,若𝑡𝑛𝑥和𝑡𝑛𝑦都很大,则附数并不适用,说明此点非最高亮度点,应当跳过该点并继续扫描其他像素点。具体在实际提取激光线中心点时,若𝑡𝑛𝑥和𝑡𝑛𝑦都小于0.5则视为极值点位可以将此点视为激光线的中心点进行保存。
光平面方程求解
在光平面标定中,线性方程组解法的核心目标是通过已知的三维空间点坐标,求解光平面的数学方程参数
L: aXc+bYc+cZc+d=0(2-1) L: \; aX_c + bY_c + cZ_c+d = 0 \tag{2-1} L:aXc+bYc+cZc+d=0(2-1)
标定的本质是通过观测数据确定这四个参数.可以通过建立相机像素坐标与世界坐标系坐标之间的线性关系来求解线性方程,从而确定光平面参数。具体来说,其线性关系如
假设通过实验测得光平面上的𝑛个三维点坐标,记为𝑃𝑖=(𝑥𝑖,𝑦𝑖,𝑧i,其中i=1,2,⋯𝑛)𝑃_𝑖 = (𝑥_𝑖, 𝑦_𝑖, 𝑧_i ,其中i = 1,2, ⋯ 𝑛)Pi=(xi,yi,zi,其中i=1,2,⋯n)。根据平面方程的定义,每个点都需要满足光平面方程。
实际上在进行平面标定时,会将双目相机及激光发生器固定,并移动标定板(也可以是单目, 如果是单目, 就要求在相机坐标系下的三维点坐标)拍摄𝑛个位姿下定板上投射出的激光线图像。
通过上一节的激光线中心点提取的方法,提取到的第 i个位姿下的标定板上的k个激光线中心点的像素坐标系下二维坐标记为 (𝑢𝑖1,𝑣𝑖1),(𝑢𝑖2,𝑣𝑖2),⋯,(𝑢𝑖𝑘,𝑣𝑖𝑘){(𝑢𝑖_1, 𝑣𝑖_1), (𝑢𝑖_2, 𝑣𝑖_2), ⋯ , (𝑢𝑖_𝑘, 𝑣𝑖_𝑘)}(ui1,vi1),(ui2,vi2),⋯,(uik,vik),其中𝑖 = 1,2,
有激光线中心点像素坐标通过双目相机标定得到的相机内参转化为世界坐标系下
的𝑚个点的三维坐标(𝑥1,𝑦1,𝑧1),(𝑥2,𝑦2,𝑧2),⋯,(𝑥𝑖,𝑦𝑖,𝑧𝑖),⋯,(𝑥𝑚,𝑦𝑚,zm){(𝑥_1, 𝑦_1, 𝑧_1), (𝑥_2, 𝑦_2, 𝑧_2), ⋯ , (𝑥_𝑖, 𝑦_𝑖, 𝑧_𝑖), ⋯ , (𝑥_𝑚, 𝑦_𝑚,z_m)}(x1,y1,z1),(x2,y2,z2),⋯,(xi,yi,zi),⋯,(xm,ym,zm)
位姿下拍摄标定板上的激光线的原理如图2- 4所示:
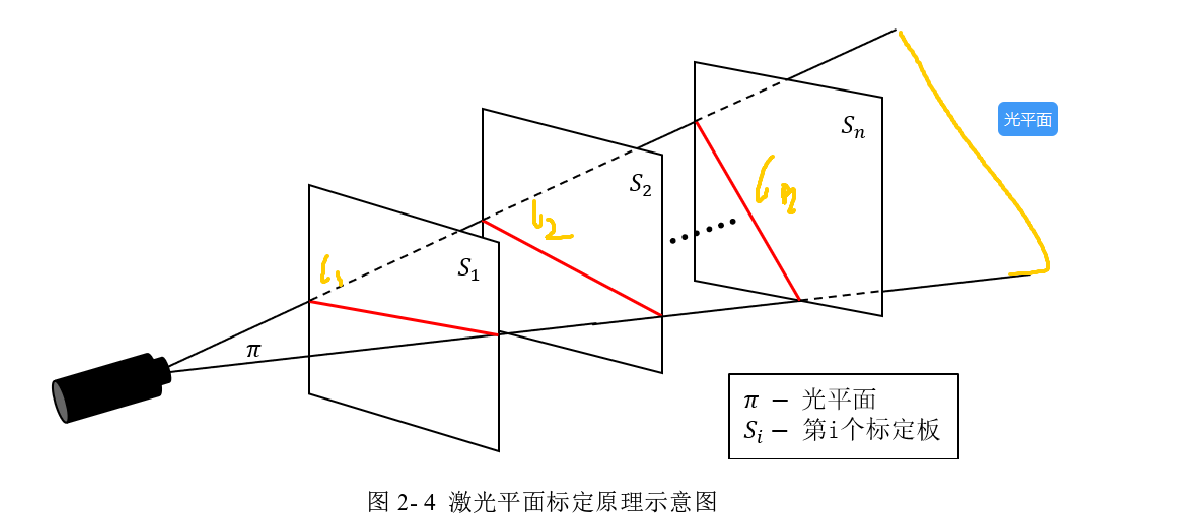
如图所示红色线条为线激光发射器在标定板上投射的激光线。通过激光线中心点提取将所有𝑚个点的方程联立,形成线性方程组如
{Ax1+By1+Cz1+D=0Ax2+By2+Cz2+D=0⋮Axm+Bym+Czm+D=0(2-2) \begin{cases} Ax_1 + By_1 + Cz_1 + D = 0 \\ Ax_2 + By_2 + Cz_2 + D = 0 \\ \vdots \\ Ax_m + By_m + Cz_m + D = 0 \end{cases}\tag{2-2} ⎩ ⎨ ⎧Ax1+By1+Cz1+D=0Ax2+By2+Cz2+D=0⋮Axm+Bym+Czm+D=0(2-2)
该方程组可以表示为矩阵形式如{2-3}所示
Mv=0(2-3) Mv = 0\tag{2-3} Mv=0(2-3)
M=[x1y1z11x2y2z21⋮⋮⋮⋮xmymzm1],v=[ABCD] M = \begin{bmatrix} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ \vdots & \vdots & \vdots & \vdots \\ x_m & y_m & z_m & 1 \end{bmatrix}, \quad v = \begin{bmatrix} A \\ B \\ C \\ D \end{bmatrix} M= x1x2⋮xmy1y2⋮ymz1z2⋮zm11⋮1 ,v= ABCD
参考资料:
1\]赵旭.基于双目多线及点云全局注册的三维重建系统设计与优化\[D\].电子科技大学,2025.DOI:10.27005/d.cnki.gdzku.2025.005101. \[2\]丁高见.线结构光三维视觉测量传感器标定技术研究\[D\].河南工业大学,2024.DOI:10.27791/d.cnki.ghegy.2024.000300.