本节主要讲解下平面约束,如家庭用的扫地机器人,其运动基本上是在平面上,如果你利用视觉或IMU等的传感器去融合,就会引入高度上的累积误差,这时候一个地面约束的假设存在,能有效消除累积误差,接下来我们看如何构建地面约束。
完整版代码![]() https://gitee.com/zl_vslam/slam_optimizer/blob/master/3d_optimize/apps/main_ch14.cpp
https://gitee.com/zl_vslam/slam_optimizer/blob/master/3d_optimize/apps/main_ch14.cpp
一. 问题描述
示意图如下
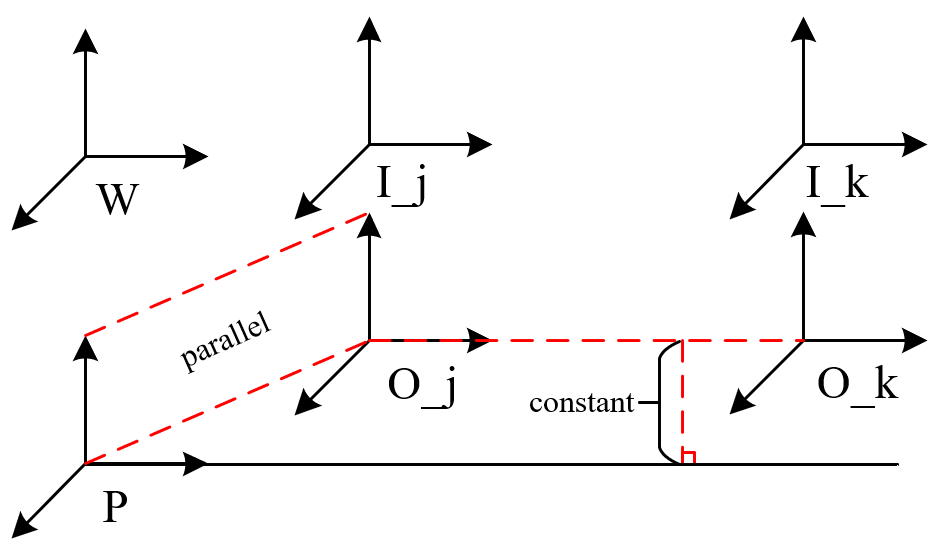
地面约束可以简单描述为:1. P系的z轴和O系的z轴时钟平行;2. O系到P系的XOY平面的距离始终恒定。这里是较为复杂的坐标系对齐,实际上,对于我们单纯介绍地面约束,忽略掉外参,因此有两个残差项;
平面约束条件:
-
方向约束:物体坐标系的Z轴应该与平面法线对齐
-
高度约束:物体原点在平面法线方向上的投影应为0
残差项一:
Odometry坐标系的姿态与平面坐标系的姿态误差应该只有绕Z轴的旋转,roll、pitch都是0;
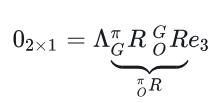
残差项二:
在全局坐标系下,z轴方向应该固定,如0或者先验高度值,因此将当前坐标系的z转到全局下,应该等于这个固定值,残差为0;
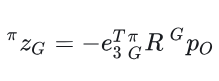
上面说了忽略外参,以及假设高度为0,因此
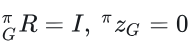
仔细观察这两个残差,实际上就是让旋转ROG的右上角2x1向量为0,实际就是roll, pitch为0以及平移z方向为0
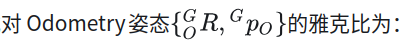
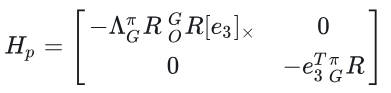
这个推导比较简单只需要利用右扰动,然后进行一阶近似即可,这个推导相对比较简单,这里展示了开源方案的结果,只进行说明,不进行详细推导,下一讲将会从原理上详细推导残差跟雅克比,并给出相应的代码验证。
注意:上述中的正负号区别,无非就是观测减预测或者预测剑观测的区别,观测是三个0
二. 结果展示
开源项目中的代码段,残差与雅克比矩阵如下
void ComputePlaneConstraintResidualJacobian(const Eigen::Matrix3d& G_R_O, const Eigen::Vector3d& G_p_O,
Eigen::Vector3d* res, Eigen::Matrix<double, 3, 6>* H) {
const Eigen::Matrix3d pi_R_G = Eigen::Matrix3d::Identity();
const double pi_z_G = 0.;
Eigen::Matrix<double, 2, 3> Lambda;
Lambda << 1., 0., 0.,
0., 1., 0.;
const Eigen::Vector3d e3(0., 0., 1.);
res->head<2>() = -Lambda * pi_R_G * G_R_O * e3;
(*res)[2] = pi_z_G + e3.transpose() * pi_R_G * G_p_O;
H->setZero();
H->block<2, 3>(0, 0) = -Lambda * pi_R_G * G_R_O * TGK::Util::Skew(e3);
H->block<1, 3>(2, 3) = -e3.transpose() * pi_R_G;
}本节用在了上节仿真的位姿图优化框架中,利用g2o直接就退出了,时间有限,就没有细查,g2o代码如下
virtual void computeError() override {
// 获取位姿顶点
Sophus::SE3d pose = (static_cast<VertexSE3LieAlgebra*> (_vertices[0]))->estimate();
// 获取 SE(3) 位姿
const Eigen::Matrix3d G_R_O = pose.rotationMatrix();
const Eigen::Vector3d G_p_O = pose.translation();
// 提取平面参数
const Eigen::Matrix3d& pi_R_G = plane_params_.pi_R_G;
const double& pi_z_G = plane_params_.pi_z_G;
// 选择矩阵:取向量的前两个分量
Eigen::Matrix<double, 2, 3> Lambda;
Lambda << 1.0, 0.0, 0.0,
0.0, 1.0, 0.0;
// Z 轴单位向量
const Eigen::Vector3d e3(0.0, 0.0, 1.0);
// 计算残差
Eigen::Vector3d error;
// 前两个残差:方向约束
// O 坐标系的 Z 轴在平面坐标系下的投影应该为零(即与平面法线对齐)
error.head<2>() = -Lambda * pi_R_G * G_R_O * e3;
// 第三个残差:高度约束
// 位姿原点在平面法线方向上的投影应该等于平面高度
error[2] = pi_z_G + e3.transpose() * pi_R_G * G_p_O;
// cout << "G_p_O ======= :" << G_p_O.transpose() << endl;
// cout << "error ======= :" << error.transpose() << endl;
_error = error;
}
virtual void linearizeOplus() override {
// 获取位姿顶点
Sophus::SE3d pose = (static_cast<VertexSE3LieAlgebra*> (_vertices[0]))->estimate();
const Eigen::Matrix3d G_R_O = pose.rotationMatrix();
// 平面参数
const Eigen::Matrix3d& pi_R_G = plane_params_.pi_R_G;
// 选择矩阵
Eigen::Matrix<double, 2, 3> Lambda;
Lambda << 1., 0., 0.,
0., 1., 0.;
// Z 轴单位向量
const Eigen::Vector3d e3(0., 0., 1.);
// 反对称矩阵工具函数
auto skew = [](const Eigen::Vector3d& v) -> Eigen::Matrix3d {
Eigen::Matrix3d S;
S << 0., -v.z(), v.y(),
v.z(), 0., -v.x(),
-v.y(), v.x(), 0.;
return S;
};
// 雅可比矩阵:3x6 (残差维度 x 位姿维度)
Eigen::Matrix<double, 3, 6> J = Eigen::Matrix<double, 3, 6>::Zero();
// 对旋转部分的雅可比 (前 3 个自由度)
// 对应残差的前两个分量对旋转的导数
J.block<2, 3>(0, 0) = -Lambda * pi_R_G * G_R_O * skew(e3);
// 对平移部分的雅可比 (后 3 个自由度)
// 对应残差的第三个分量对平移的导数
J.block<1, 3>(2, 3) = -e3.transpose() * pi_R_G;
// cout << "J ======= :" << J << endl;
// 设置雅可比矩阵
_jacobianOplusXi = J;
}这里利用ceres-solver自动求导,来验证这个问题,接下来我们看效果
template <typename T>
bool operator()(const T* const p_a_ptr,
const T* const q_a_ptr,
T* residuals_ptr) const {
Eigen::Map<const Eigen::Matrix<T, 3, 1>> p_a(p_a_ptr);
Eigen::Map<const Eigen::Quaternion<T>> q_a(q_a_ptr);
// q_a.normalize();
const Eigen::Matrix<T, 3, 3> G_R_O = q_a.toRotationMatrix();
const Eigen::Matrix<T, 3, 1> G_p_O = p_a;
// 提取平面参数
const Eigen::Matrix<T, 3, 3> pi_R_G = Eigen::Matrix<T, 3, 3>::Identity();
const T pi_z_G = T(0.0);
// 选择矩阵:取向量的前两个分量
Eigen::Matrix<T, 2, 3> Lambda;
Lambda << T(1.0), T(0.0), T(0.0),
T(0.0), T(1.0), T(0.0);
// Z 轴单位向量
const Eigen::Matrix<T, 3, 1> e3(T(0.0), T(0.0), T(1.0));
Eigen::Map<Eigen::Matrix<T, 3, 1>> residuals(residuals_ptr);
// 前两个残差:方向约束
// O 坐标系的 Z 轴在平面坐标系下的投影应该为零(即与平面法线对齐)
// residuals.template head<2>() = -Lambda * pi_R_G * G_R_O * e3;
// // 第三个残差:高度约束
// // 位姿原点在平面法线方向上的投影应该等于平面高度
// residuals[2] = pi_z_G + e3.transpose() * pi_R_G * G_p_O;
// 前两个残差:方向约束
// 显式计算矩阵乘法以避免表达式模板问题
Eigen::Matrix<T, 3, 1> temp1 = G_R_O * e3; // R * e3
Eigen::Matrix<T, 3, 1> temp2 = pi_R_G * temp1; // pi_R_G * (R * e3)
residuals.template head<2>() = -Lambda * temp2; // -Lambda * (pi_R_G * R * e3)
// 第三个残差:高度约束
// 同样显式计算避免表达式模板
Eigen::Matrix<T, 3, 1> temp3 = pi_R_G * G_p_O; // pi_R_G * p
T height_term = e3.transpose() * temp3; // e3^T * pi_R_G * p
residuals[2] = pi_z_G + height_term;
// residuals = sqrt_information_ * residuals;
Eigen::Matrix<T, 3, 3> sqrt_info_T;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
sqrt_info_T(i, j) = T(sqrt_information_(i, j));
}
}
residuals = sqrt_info_T * residuals;
return true;
}最终效果展示

加上平面约束,总体上效果变好了,这里图中不明显,我们来看看数据,下图是没加平面约束前的结果,可以看最后一列,z轴快飘半米了
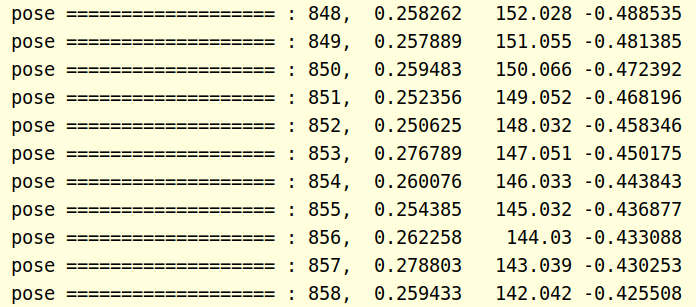
接下来看看加了平面约束的情况
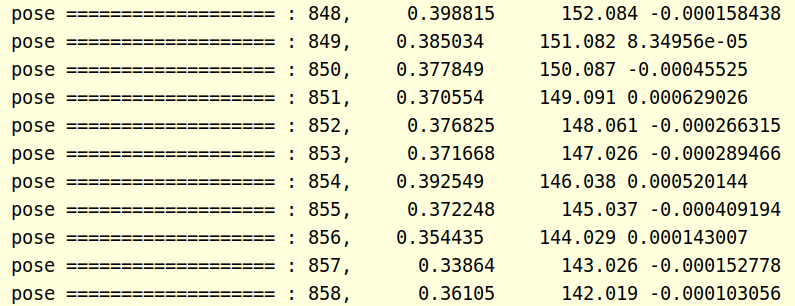
从图中可以看到,最后一列接近于0了,因此能够证明算法的有效性。
总结
本节总结了平面约束的基本原理,实际上从直观上来讲,平面约束其实就是把roll, pitch以及z强制往0上拉,让一个3D系统变更为类似2D系统,但是凡是都有两面性,选择合适的场景应用很重要。
参考文献:《VINS on wheels》
