
标题:《3D Gaussian Flats: Hybrid 2D/3D Photometric Scene Reconstruction》
项目:https://theialab.github.io/3dgs-flats/
来源:Simon Fraser University;University of Toronto;University of Bologna
文章目录
摘要
辐射场技术与新型视图合成方法的突破性进展,使得从照片中生成逼真数字孪生体成为可能。然而现有方法在处理平面无纹理表面时存在明显局限,由于光度重建目标函数条件欠佳,导致重建效果出现不均匀和半透明现象 。虽然表面重建方法能解决这一问题,但会牺牲视觉质量。 我们提出了一种创新的2D/3D混合表征方案,通过联合优化约束平面(2D)高斯函数建模平面表面,同时采用自由形式(3D)高斯函数处理场景其他区域 。该端到端方法能动态检测并优化平面区域,同时提升视觉保真度与几何精度。在ScanNet++和ScanNetv2数据集上,该方案实现了最先进的深度估计效果,并在网格提取方面表现优异,且无需过度拟合特定相机模型,充分展现了其在室内场景高质量重建中的卓越性能。
给定 N N N张待处理图像{ I c I_c Ic}和 M M M个平面表面{ P p P_p Pp}(每个表面由二值图像mask { M p , c M_{p,c} Mp,c}定义),目标是通过2DGS基元精确还原并紧凑表示平面表面,同时使用3DGS基元对场景其余部分进行建模,关键在于避免使用三维基元建模平面表面时常见的伪影问题(参见图1)。
一、混合表示
该表示由 M M M个平面 P = P= P={ P p P_p Pp}组成,每个平面均以其三维原点和法线 ( o p , n p ) (o_p,n_p) (op,np)为特征。每个平面 P p P_p Pp的几何结构通过一组二维高斯函数 G = G= G={ g k g_k gk} k = 1 K k ^{K_k}_{k=1} k=1Kk来表示:
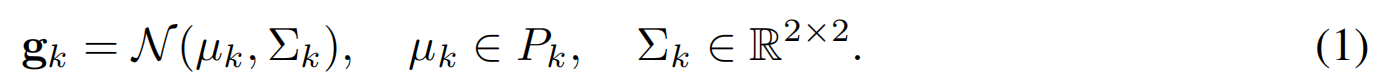
其中, µ k µ_k µk 是平面 P p P_p Pp上第 k k k个2DGS中心, Σ k Σ_k Σk 是二维协方差矩阵,其参数化由二维平面内旋转矩阵 R k R_k Rk和二维对角尺度矩阵 S k S_k Sk构成。平面到世界坐标系的齐次变换矩阵: T p w = h o m ( R , o ) T_{pw}=h_{om}(R,o) Tpw=hom(R,o),其中 R R R是满足 z ^ = R n \hat{z} =Rn z^=Rn的任意旋转矩阵, z ^ \hat{z} z^ 为世界坐标系中 z z z轴单位向量,即将平面法向量 n n n对齐到世界坐标 Z Z Z轴 (平面GS-->刚性变换-->世界坐标系):
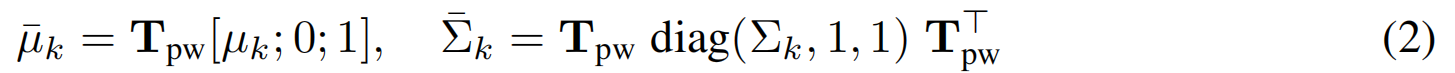
上述得到了适用于渲染的标准3DGS;场景其余几何结构由无约束的3DGS G ˉ = \bar{G}= Gˉ={ g ˉ k \bar{g}k gˉk} k = 1 K ˉ ^{\bar{K}}{k=1} k=1Kˉ 表示:
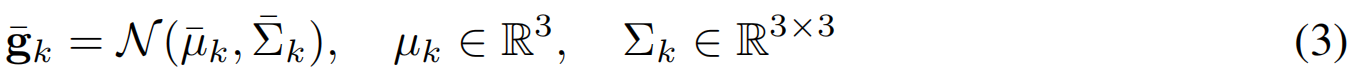
所有高斯均采用球面谐波表示视点相关颜色c和不透明度 α。为通过混合表示法重建场景,需对平面P、二维平面高斯函数G及三维自由形式高斯函数 G ˉ \bar{G} Gˉ的自由度进行优化:首先采用仅含3DGS的预热阶段(共N=3500次迭代),随后进入平面重建阶段。每轮优化:
- (i) 通过稳健拟合当前表示动态初始化平面参数;
- (ii)交替优化平面与高斯参数;
- (iii)采用MCMC 密度化方法提升表示密度,以应对紧支函数优化的挑战。
二、平面的初始化
简化表示:第 c c c个视图的第 p p p个平面的二元mask: M ← M c , p M←M_{c,p} M←Mc,p, π π π 表示三维点投影到第 n n n个图像的函数。首先筛选GS:(i)均值投影到mask内,(ii)具有足够不透明度,(iii)位于第n个图像预期射线终止的壳层内:
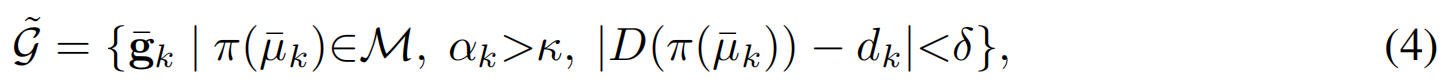
阈值 α t h = 0.1 α_{th} =0.1 αth=0.1和 d t h = 0.05 d_{th}=0.05 dth=0.05, D D D为预期射线终止图(深度图), d k d_k dk为高斯函数的深度。随后,我们通过对采样高斯函数的点云进行 RANSAC 优化来提取候选平面P:
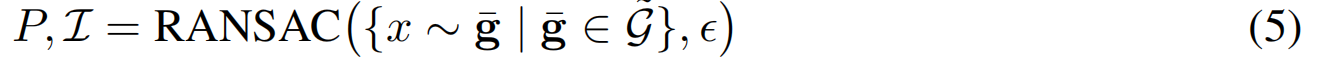
仅当平均内点残差低于 ϵ ϵ ϵ 时,才将 P P P视为可行的平面候选。集合 I I I包含 G ~ \tilde{G} G~中作为 RANSAC 过程内点的高斯索引。若平面尺寸过小( I I I规模小于100),则进一步剔除。一旦接受对应 M M M的平面,该平面 p p p的所有语义mask将被排除在后续 RANSAC 运行之外。对于剩余mask,重复平面初始化过程。
随后,将发现的内点从3DGS集合 G ← G ˉ / I ˉ G ←\bar{G} / \bar{I} G←Gˉ/Iˉ 中移除,并将其添加至2DGS集合 G ← G ∪ I G ← G∪I G←G∪I。通过将3DGS转换为局部平面坐标系 ,将其裁剪为2D平面分布,并将其中心值和尺度的第三分量设为零。此外,仅保留局部平面坐标系中绕z轴的旋转。
活动集合的更新 :若待接受平面 P i P_i Pi与现有平面的夹角距离低于阈值,且其原点 o i o_i oi与该平面最近高斯中心的欧氏距离较短,则合并两个平面。否则将该平面作为新平面添加至平面集合P的活动集中。合并过程中,新平面的GS将被分配至先前已识别的平面。该机制可实现对在任一视图中仅被部分观测到的平面区域进行整合优化。
三、优化
采用 block-coordinate 下降法 优化模型表示,每轮开始时仅对平面参数优化10次迭代,随后冻结,对2D和3DGS参数进行另外100次迭代优化。这种交替优化策略对避免模型不稳定至关重要(图7中的消融实验可见)。在第一轮优化中,每次迭代都会通过损失函数优化第 c c c张图像中第 p p p个平面的参数:
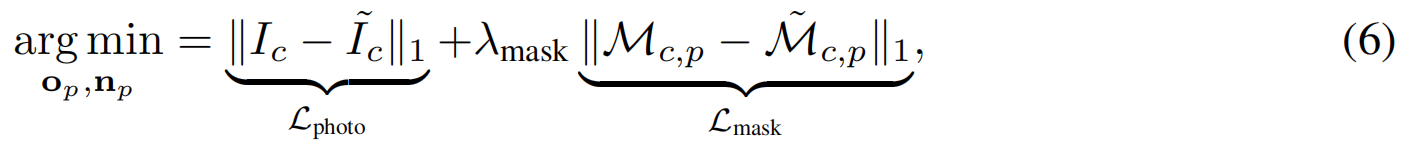
其中 M ~ \tilde{M} M~为预测的平面mask,通过渲染高斯混合模型获得(二值化颜色:平面为白色,三维为黑色),并在光栅化过程中使用原始高斯不透明度进行alpha混合。在第二次优化模块中,联合优化所有高斯参数:
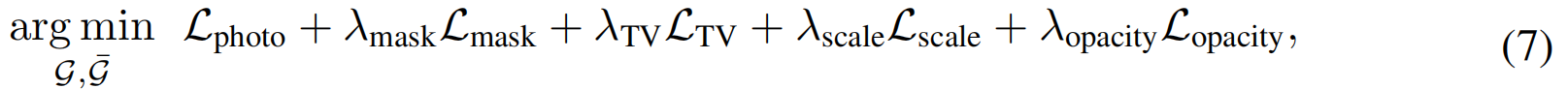
LTV 为总深度变化正则化项,Lscale为尺度正则化项,Lopacity为不透明度正则化,用于消除不受测光损失约束的高斯尺寸。平面高斯在平面优化(6)过程中发生刚性位移,而在高斯优化(7)过程中仅发生平面内局部位移,因为其二维平面内参数被优化。
四、平面重定位
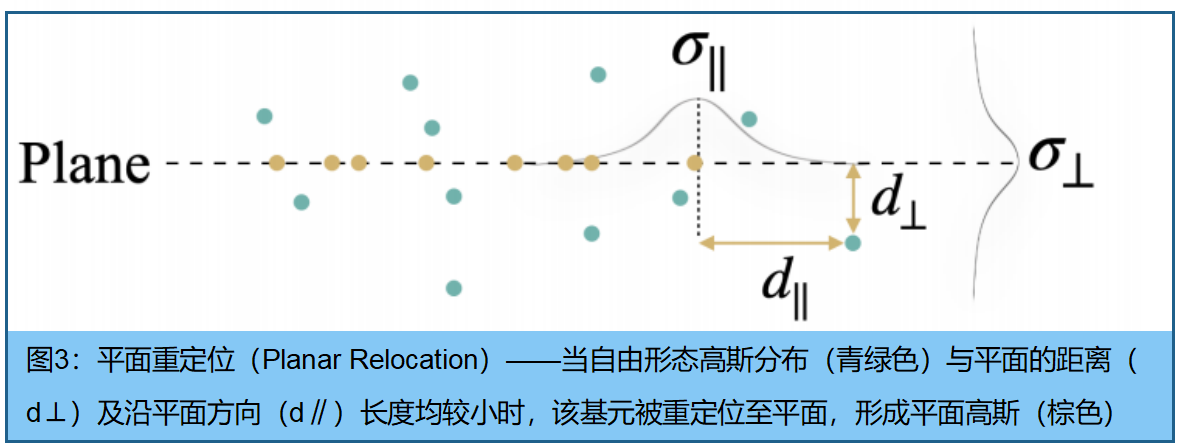
训练动态中,采用3DGS MCMC。为实现平面的密度增强,通过将低不透明度高斯重新定位到高不透明度高斯密集区域,从而实现3D与2D/平面高斯之间的转换。然而,当平面纹理较弱时,平面上的高斯数量通常较少,导致平面/平面高斯的密度增强速度较慢 。为解决这一问题,每当自由形式高斯分布投影到当前掩模 π ( µ ˉ k ) ∈ M π(\bar{µ}k)∈M π(µˉk)∈M且与当前重建结果足够接近时,我们就会随机将其重新定位到该平面。为测量距离,我们选取与 µ ˉ k \bar{µ}k µˉk欧氏距离最小的2DGS,并测量其在平面法线 d ⊥ d⊥ d⊥方向和平面 d ∥ d∥ d∥方向的距离(图3)。若两个距离均足够小,则通过以下伯努利分布进行随机重定位:
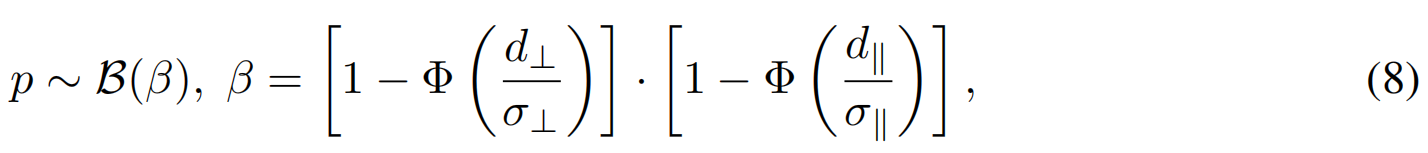
其中 Φ Φ Φ 是一个高斯基元的累积分布函数,用于将距离映射为概率。伯努利分布相当于一个随机过滤器。 σ ⊥ σ_⊥ σ⊥和 σ ∥ σ_∥ σ∥是控制随机重定位的超参数
实验
1.新视角合成
数据集 。常见室内场景基准数据集ScanNet++和ScanNetv2 (主要包含适合当前任务的平面无纹理室内场景)。 ScanNet++提供带有SfM相机位姿的密集场景和稀疏点云,主要适用于遵循NeRF[5]范式的三维重建方法。而传统版本的ScanNet(即ScanNetv2)则提供缺乏SfM信息的稀疏视角。我们的方法支持使用或不使用初始稀疏点云,既能在ScanNet++上使用稀疏SfM点云进行初始化重建,也能在ScanNetv2上使用随机初始化点云进行实验。针对ScanNet++,我们采用11个带有真实网格的训练场景进行深度推导,利用iPhone视频流数据,以2倍下采样率每10帧采样一次用于训练,每8帧采样一次用于测试。我们选择的内容丰富且包含多种平面表面的场景。对于ScanNet,我们按照[27]的数据准备方案,在5个具有足够平面表面重叠视角的场景上进行评估 。二维平面mask通过PlaneRecNet[25]生成,并通过SAMv2视频处理器在图像序列中传播 。PlaneRecNet是一种从单个RGB图像中同时检测平面实例并重建3D场景的深度学习方法。其核心创新在于通过跨任务一致性(Cross-Task Consistency),深度融合了实例分割与深度估计两个子任务,让它们在学习过程中互相监督、互为优化,从而提升整体性能
Baseline。在三维表示方面,采用标准3DGS和3DGS- MCMC进行对比,后者对随机初始化更具鲁棒性且渲染质量更高。光学表面重建,采用2DGS[7],以及近期在深度质量方面取得改进的 PGSR [16]和RaDe-GS[17]进行对比。所有方法均经过30K次迭代训练。
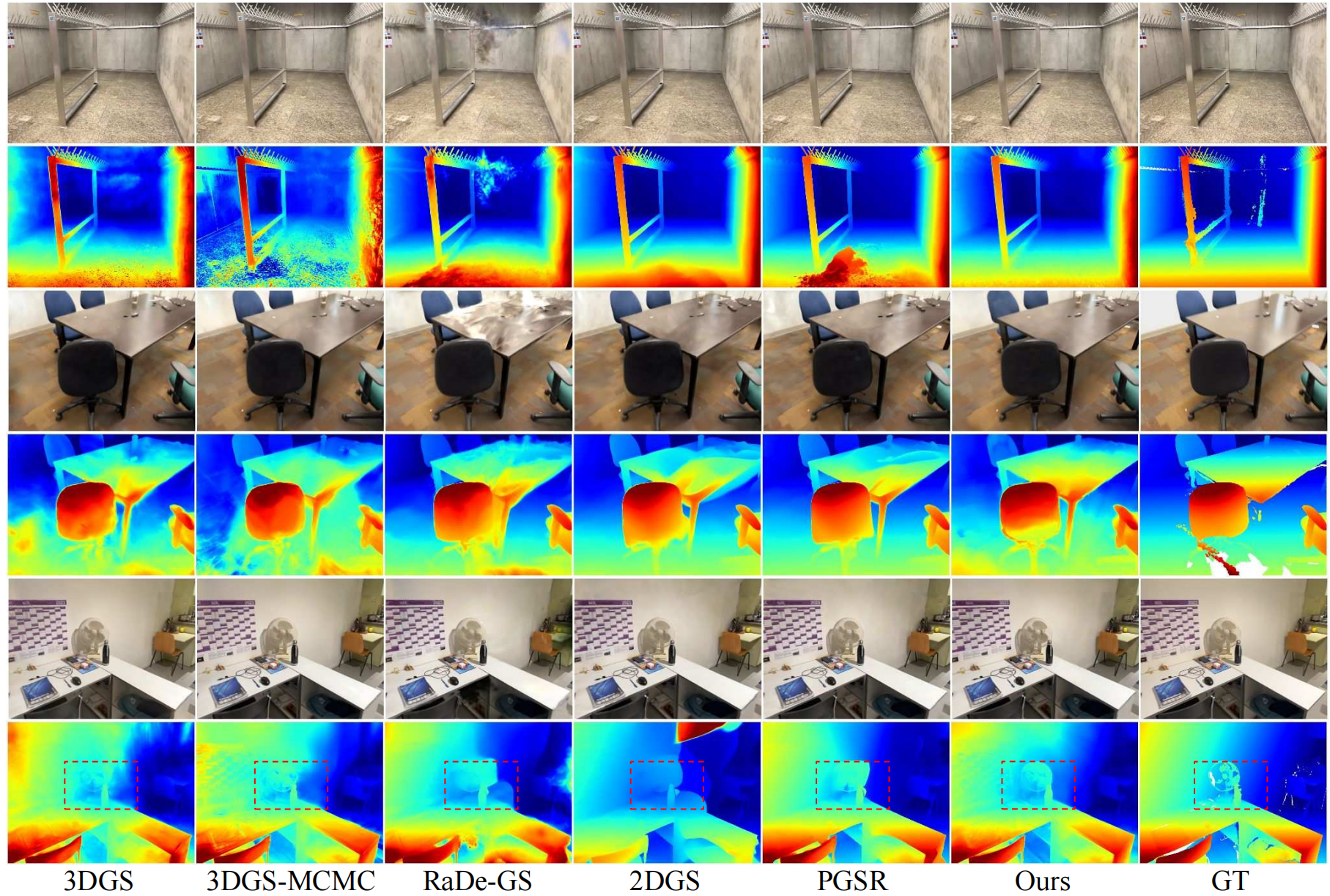
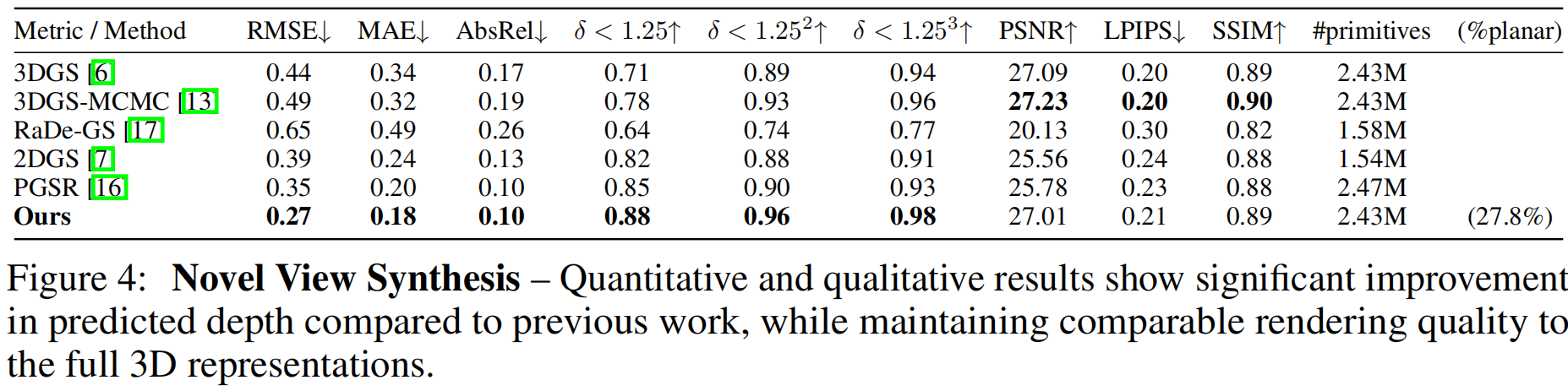
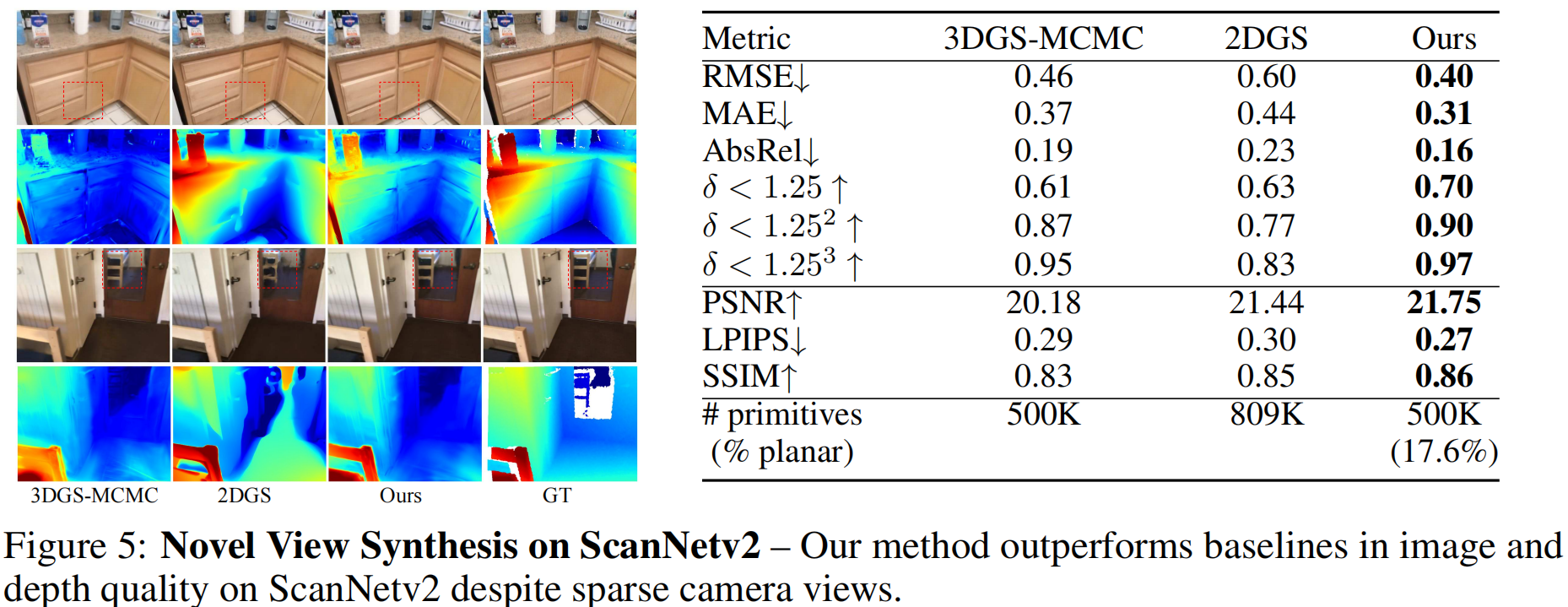
对两个数据集的定量与定性分析表明,相较于所有基准方法,我们的深度精度均显著提升。值得注意的是,在密集的ScanNet++场景中,不仅实现了与 SOTA 三维表征相当的图像质量,更在深度质量上更胜一筹------定性案例中更清晰的几何重建便是明证。与三维方法的 PSNR 差异虽小,实则体现了二者间的权衡:我们的约束几何确保了结构正确性,而无约束方法则可能因采用视点依赖效应而通过错误几何结构放大 PSNR 。
2.网格提取
我们的方法能够从重建的三维平面表面中提取网格。针对每个平面,我们通过计算射线-平面交点将所有二维分割mask反投影到三维空间,生成点云。该点云采用固定尺寸体素进行降采样,并通过光栅化转换到平面坐标系,构建出占用网格。随后运用Marching Squares 提取轮廓(剔除点数不足100的小轮廓),再通过ear-clipping triangulation 生成最终网格。
数据集 采用ScanNet++提取平面表面网格。实验结果同时展示了iPhone拍摄数据子集和 DSLR 数据子集的表现,表明本方法能兼容不同相机型号,而传统方法往往仅能适配单一模态。为获取真实平面网格,采用Watson等人[9]的方法。随后仅选取真实网格中已标注分割掩码的平面子集进行分析。
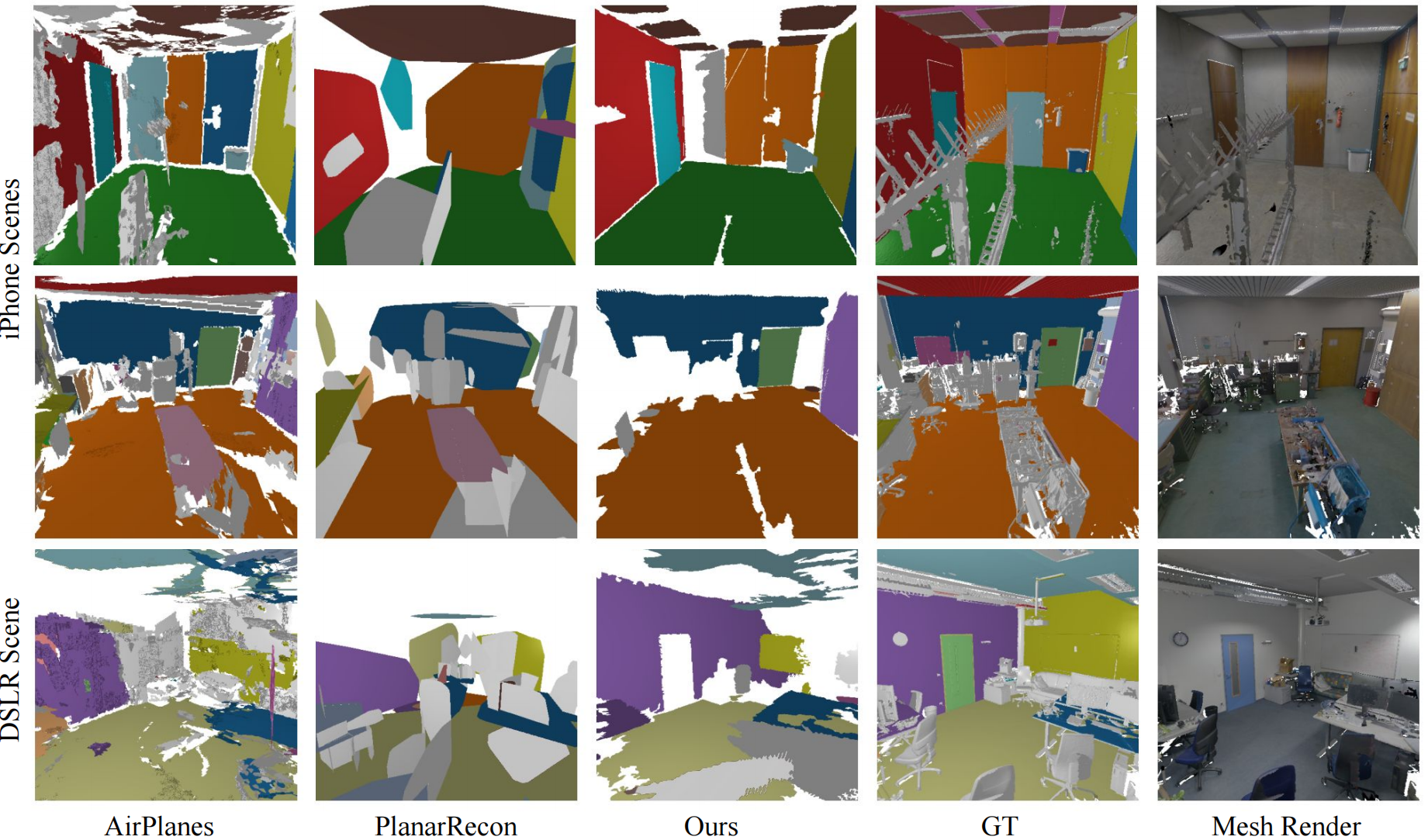
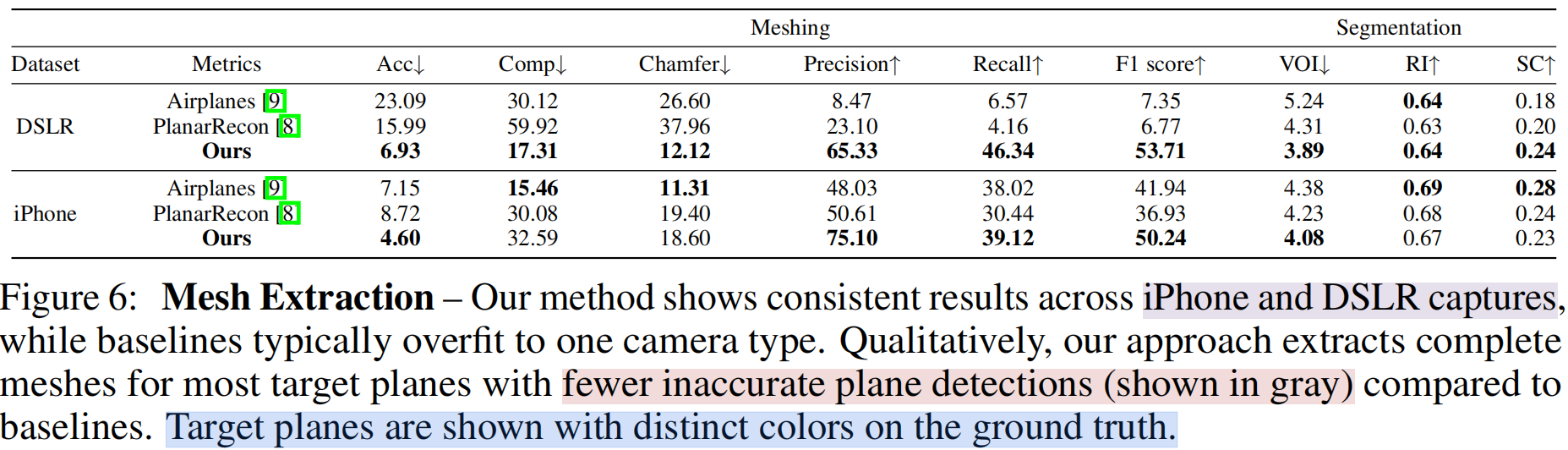
我们的方法在数据集的 DSLR 图像子集上表现优于基线方法。与以往仅针对特定模态(如手机摄像头)训练、难以迁移至不同相机型号(如 DSLR 摄像头)的方法不同,我们的方案通过光度重建技术在测试场景中实现零样本网格提取,从而保持网格质量的一致性。此外,在iPhone数据集上,我们的方法优于PlanarRecon,同时与AirPlanes具有可比性能。定性分析表明,PlanarRecon和AirPlanes均会提取出带有大量随机小碎片的多余平面,导致网格既难看又不实用。相比之下,我们的方法生成的平面表面干净整洁,重建效果更加连贯实用。