平面运动模型下的特性及应用

针孔相机模型（Pinhole Camera Model）是计算机视觉和摄影测量中最基础、最常用的成像模型。它描述了三维世界中的点是如何投影到二维图像平面上的。

详细推导可见针孔相机模型

基本定义

先定义四个坐标系：

世界坐标系 (World Coordinate System, O w O_w Ow): 真实世界的绝对坐标系，点记为 ( X w X_w Xw, Y w Y_w Yw, Z w Z_w Zw)。
相机坐标系 (Camera Coordinate System, O c O_c Oc): 以相机光心（针孔）为原点，Z轴为光轴（指向前方），点记为 ( X c X_c Xc, Y c Y_c Yc, Z c Z_c Zc)。
图像物理坐标系 (Image Plane Coordinate System, o): 位于光心前方焦距 f 处（为了方便计算，通常使用"虚拟成像平面"在前，避免图像倒立），单位通常是毫米，点记为 (x, y)。
像素坐标系 (Pixel Coordinate System, uv): 也就是我们最终看到的数字图像，原点通常在图像左上角，单位是像素，点记为 (u, v)。

这种特定的约束（绕 Y 轴旋转，平移仅限 X-Z 平面）在计算机视觉中非常常见，通常被称为 "平面运动模型" (Planar Motion Model)。这常见于在平坦地面上行驶的自动驾驶汽车或移动机器人。

这种约束会极大地简化针孔相机模型的推导结果，最核心的结论是：垂直方向（Y轴/v坐标）的投影变得非常简单且独立。

以下是详细的推导和简化分析：

1. 简化的外参矩阵

这种约束下，相机的运动受到以下限制：

旋转矩阵 R ：只有绕 Y 轴的旋转（通常称为 Yaw/偏航角 ，记为 θ \theta θ）。
平移向量 t ：只有 X 和 Z 分量（即相机高度不变， t y t_y ty = 0）。

旋转矩阵 R y ( θ ) R_y(\theta) Ry(θ)

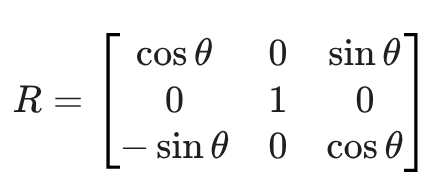
平移向量 t t t

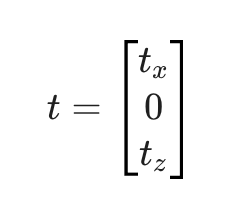
2. 推导相机坐标系 P c P_c Pc

将世界坐标 P w = $X w , Y w , Z w$ T P_w = $X_w, Y_w, Z_w$ ^T Pw= $Xw,Yw,Zw$ T 转换到相机坐标 P c = $X c , Y c , Z c$ T P_c = $X_c, Y_c, Z_c$ ^T Pc= $Xc,Yc,Zc$ T：

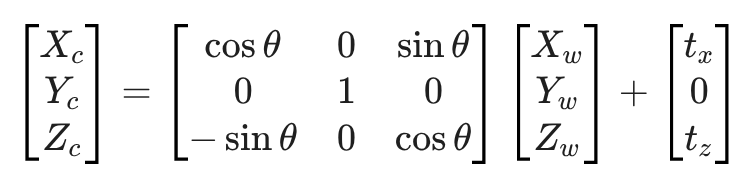
展开计算得到三个分量：

X c = X w cos ⁡ θ + Z w sin ⁡ θ + t x X_c = X_w \cos\theta + Z_w \sin\theta + t_x Xc=Xwcosθ+Zwsinθ+tx
Y c = Y w Y_c = Y_w Yc=Yw
Z c = − X w sin ⁡ θ + Z w cos ⁡ θ + t z Z_c = -X_w \sin\theta + Z_w \cos\theta + t_z Zc=−Xwsinθ+Zwcosθ+tz

3. 推导像素坐标 (u, v)

代入针孔投影公式：

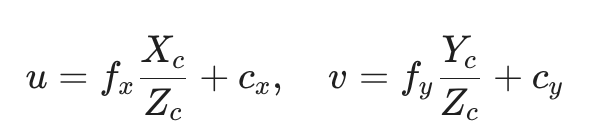
得到简化后的方程：

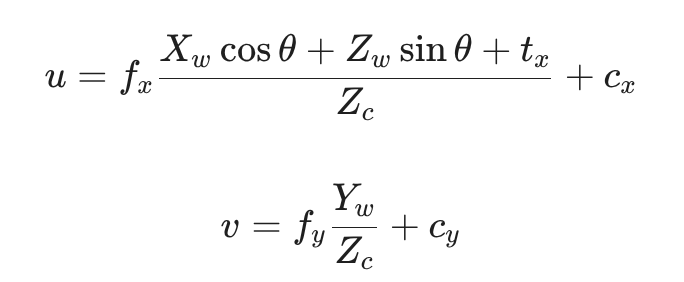
(其中 Z c = − X w sin ⁡ θ + Z w cos ⁡ θ + t z Z_c = -X_w \sin\theta + Z_w \cos\theta + t_z Zc=−Xwsinθ+Zwcosθ+tz)

4. 这种简化带来了什么？

这种约束带来了三个非常重要的几何特性，常用于车道线检测或地平面估计：

简化：地平面的投影 (Ground Plane Homography)------鸟瞰图的计算

即由 u , v u,v u,v求 X c , Z c X_c,Z_c Xc,Zc

对于地面上的点（假设地面为 Y w = H Y_w = H Yw=H，例如相机安装高度为 H H H，且向下为正），此时 Y w Y_w Yw 是常数。

那么 v v v 坐标和深度 Z c Z_c Zc 形成了一一对应的关系： v = f y H Z c + c y v = f_y \frac{H}{Z_c} + c_y v=fyZcH+cy

而 X c X_c Xc只与 u u u和 Z c Z_c Zc有关： u = f x X c Z c + c x u = f_x \frac{X_c}{Z_c} + c_x u=fxZcXc+cx

这意味着：

在平面运动模型下，只要知道一个点在图像里的 v v v 坐标（行号），并且知道相机离地高度 H H H，你就可以直接算出这个点距离你有多远 ( Z c Z_c Zc)然后就可以求出 X c X_c Xc
可以预先计算一张查找表，因为每个像素对应鸟瞰图的坐标是固定的。

总结

如果旋转只有绕 Y 轴，平移只有 X/Z：

几何上：相机在一个固定高度的水平面上滑行并左右转头。
数学上 ： Y c = Y w Y_c = Y_w Yc=Yw。
应用上：可以通过像素的 v 坐标直接反推距离（假设地面平坦），极大地降低了单目测距的难度。

代码示例：

python 复制代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

def get_bev_image(image):
    """
    演示如何从普通透视图生成鸟瞰图 (BEV)
    核心原理：将梯形区域 (ROI) 映射为矩形区域
    """
    h, w = image.shape[:2]

    # ==========================================
    # 1. 定义源点 (Source Points) - 梯形
    # ==========================================
    # 在实际工程中，这些点通常通过标定获得，
    # 或者根据"消失点"和"车头盲区"来硬编码。
    # 这里我们假设相机视野中，路面是一个梯形区域。
    
    # 梯形下底（近处）：通常覆盖整个图像宽度
    src_bottom_left = [0, h]
    src_bottom_right = [w, h]
    
    # 梯形上底（远处）：向图像中心收缩（模拟透视效果）
    # 这里的 0.4 和 0.6 是调节视野远处的宽度，越小说明看得越远（消失点附近）
    # 这里的 0.6 * h 是地平线以下的某个位置（截断天空）
    horizon_h = int(0.6 * h) 
    src_top_left = [int(0.4 * w), horizon_h]
    src_top_right = [int(0.6 * w), horizon_h]

    src_points = np.float32([src_bottom_left, src_bottom_right, src_top_left, src_top_right])

    # ==========================================
    # 2. 定义目标点 (Destination Points) - 矩形
    # ==========================================
    # 在 BEV 空间中，我们希望原来的梯形变成一个直直的矩形。
    # 这体现了"平行线在鸟瞰图中保持平行"的特性。
    
    bev_w = w # 保持宽度一致
    bev_h = h # 保持高度一致
    
    # 为了让车道线变直，我们在目标图中，
    # 让左边的点 x 坐标相同，右边的点 x 坐标相同。
    offset_x = int(0.25 * w) # 预留一些左右边距
    
    dst_bottom_left = [offset_x, bev_h]
    dst_bottom_right = [bev_w - offset_x, bev_h]
    dst_top_left = [offset_x, 0]
    dst_top_right = [bev_w - offset_x, 0]

    dst_points = np.float32([dst_bottom_left, dst_bottom_right, dst_top_left, dst_top_right])

    # ==========================================
    # 3. 计算单应性矩阵 (Homography Matrix)
    # ==========================================
    # M 就是将像素从 透视视图 -> 鸟瞰视图 的变换矩阵
    M = cv2.getPerspectiveTransform(src_points, dst_points)

    # ==========================================
    # 4. 执行变换 (Warp Perspective)
    # ==========================================
    # linear 插值即可
    bev_image = cv2.warpPerspective(image, M, (bev_w, bev_h), flags=cv2.INTER_LINEAR)

    return src_points, bev_image

def create_dummy_road_image(width=800, height=600):
    """创建一个带有透视车道线的模拟图片"""
    img = np.zeros((height, width, 3), dtype=np.uint8)
    
    # 画地平线 (天空)
    cv2.rectangle(img, (0, 0), (width, int(0.5*height)), (50, 50, 50), -1) # 灰色天空
    cv2.rectangle(img, (0, int(0.5*height)), (width, height), (100, 100, 100), -1) # 深灰路面

    # 画车道线 (透视效果：远处汇聚)
    center_x = width // 2
    vanish_y = int(0.5 * height) # 消失点在图像中心高度
    
    # 左车道线
    cv2.line(img, (center_x - 40, vanish_y), (100, height), (255, 255, 255), 10)
    # 右车道线
    cv2.line(img, (center_x + 40, vanish_y), (width - 100, height), (255, 255, 255), 10)
    
    # 画一些横向的路标 (模拟距离感)
    for i in range(1, 10):
        y = vanish_y + i * i * 6 # 越近间隔越大
        if y > height: break
        # 根据相似三角形计算宽度
        scale = (y - vanish_y) / (height - vanish_y)
        w_line = int(600 * scale)
        cv2.line(img, (center_x - w_line//2, y), (center_x + w_line//2, y), (0, 255, 255), 5)

    return img

# ==================== 主程序 ====================

# 1. 创建模拟图
original_img = create_dummy_road_image()

# 2. 生成 BEV
src_pts, bev_img = get_bev_image(original_img)

# 3. 可视化结果
plt.figure(figsize=(12, 6))

# 显示原图 + ROI 框
plt.subplot(1, 2, 1)
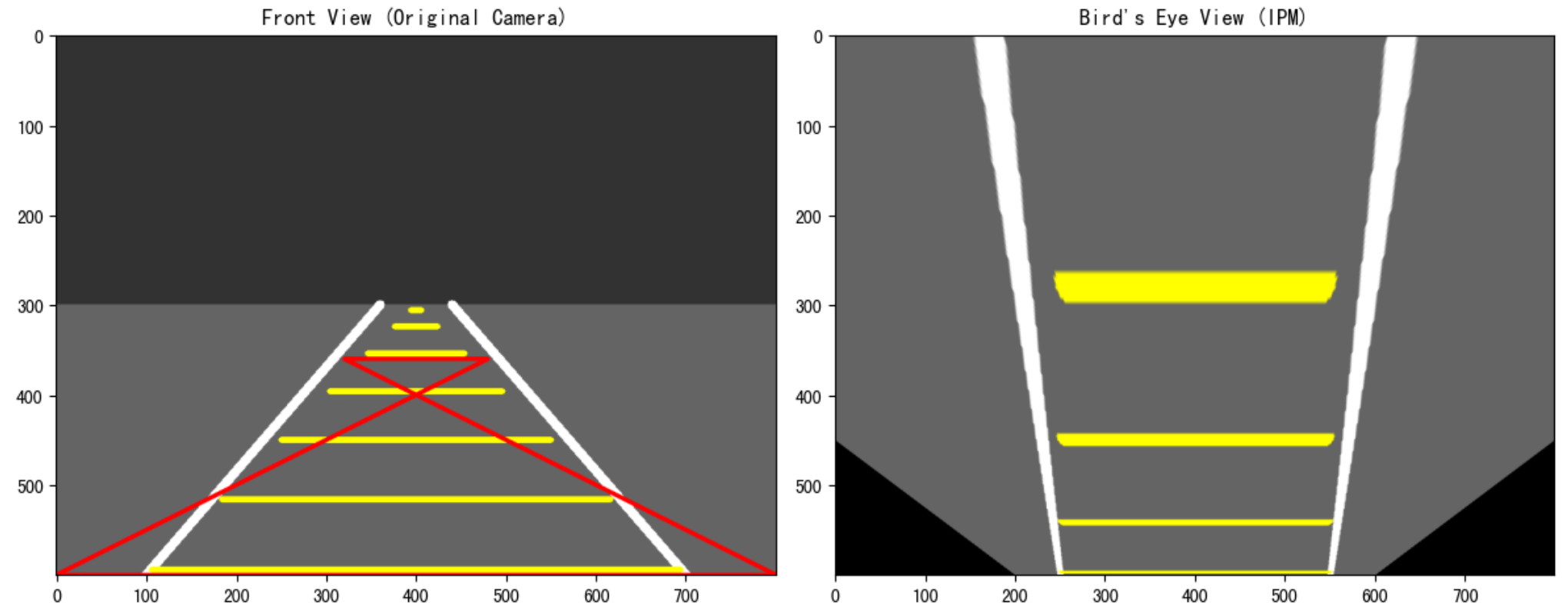
plt.title("Front View (Original Camera)")
plt.imshow(cv2.cvtColor(original_img, cv2.COLOR_BGR2RGB))
# 画出我们选择的变换区域 (梯形)
pts = src_pts.reshape((-1, 1, 2)).astype(np.int32)
cv2.polylines(original_img, [pts], True, (0, 0, 255), 3) # 红色框
plt.imshow(cv2.cvtColor(original_img, cv2.COLOR_BGR2RGB))

# 显示鸟瞰图
plt.subplot(1, 2, 2)
plt.title("Bird's Eye View (IPM)")
plt.imshow(cv2.cvtColor(bev_img, cv2.COLOR_BGR2RGB))
# 可以在这里看到，车道线变平行了，路标间隔变均匀了

plt.tight_layout()
plt.show()