数据结构 之 【模拟实现哈希表】

zl_dfq2025-09-08 10:11

目录

1.闭散列实现

1.1前提准备

[1.2 find](#1.2 find)

[1.3 insert函数](#1.3 insert函数)

插入

扩容

[1.4 erase函数](#1.4 erase函数)

2.开散列实现

2.1前提准备

[2.2 默认成员函数](#2.2 默认成员函数)

[2.3 find](#2.3 find)

[2.4 insert函数](#2.4 insert函数)

插入

扩容

[2.5 erase函数](#2.5 erase函数)

1.闭散列实现

使用除留余数法计算哈希地址，线性探测解决哈希冲突

1.1前提准备

复制代码 
namespace open_address
{
	//使用状态标记，便于插入、删除、查找
	enum STATE
	{
		EXIST,
		DELETE,
		EMPTY
	};

	template<class K, class V>
	struct HashData
	{
		pair<K, V> _kv;
		STATE _state = EMPTY;
	};

	template<class K, class V>
	class HashTable
	{
    public：

	private:
		vector<HashData<K, V>> _table;
		size_t _n; //存储的有效数据的个数
	};


}

(1)为防止与后续的开散列实现发生命名冲突，创建一个命名空间

(2)枚举出元素的状态供后续使用

(3)HashData这个类定义了哈希表所存储的数据(这里使用的是KV模型)

将HashData初始状态值为EMPTY

(4)hashTable这个类用来实现HashData的插入、删除、查找等功能

1.2 find

查找某一个元素时，我们先通过除留余数法找到对应的哈希地址，但是由于哈希冲突与线性探测解决方式的可能，如果当前位置找不到，我们就会从冲突位置开始向后寻找该元素

因为要插入的值会存放在从冲突位置开始向后的第一个EMPTY 位置，那么查找时一定是遇到第一个EMPTY位置就停止

复制代码 
HashData<const K, V>* find(const K& key)
{
	int hashi = key % _table.size();
	//由于哈希冲突的可能，所以可能需要向后找，遇到空停止
	//遇到删除继续寻找
	while (_table[hashi]._state != EMPTY)
	{
		if (_table[hashi]._state == EXIST
			&& _table[hashi]._kv.first == key)
			return (HashData<const K, V>*) & _table[hashi];
					//这里指针类型不一致，显示转换一下
		++hashi;
		hashi %= _table.size();
	}

	return nullptr;
}

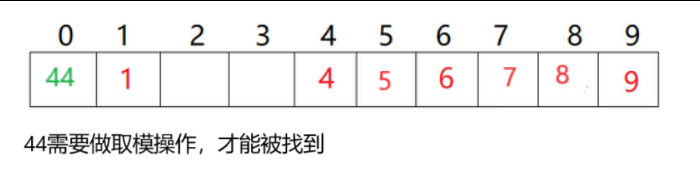
(1)并不是所有的键值key都是整型，能够做取模操作

解决方法：使用仿函数将其转换为整型

复制代码 
template<class K, class V, class HashFunc = DefaultHashFunc<K>>
class HashTable;

HashFunc hf;
int hashi = hf(key) % _table.size();

  • 默认仿函数肯定是将数值(负数，整型等)显示转换为整型

  • 但是如果键值key是字符串，我们就需要想办法将其转换为整型

    template<class K>
    struct DefaultHashFunc
    {
    size_t operator()(const K& key)
    {
    return (size_t)key;
    }
    };

    template<>
    struct DefaultHashFunc<string>
    {
    size_t operator()(const string& str)
    {
    size_t hash = 0;
    for (auto ch : str)
    hash = hash * 131 + ch;//字符串哈希算法

    复制代码 
    	return hash;
}

    };

使用模板的特化，将字符串转化为整型

处理字符串的过程中，如果只是转换字符串的首字符为整型，哈希冲突的概率极大

如果将字符串中所有字符的ASCII值相加，类似"abbc""acbb""abad"的几个字符串又会冲突

所以大佬们针对性的研究出了字符串哈希算法(小编能力有限，大家参考各种字符串Hash函数 - clq - 博客园)
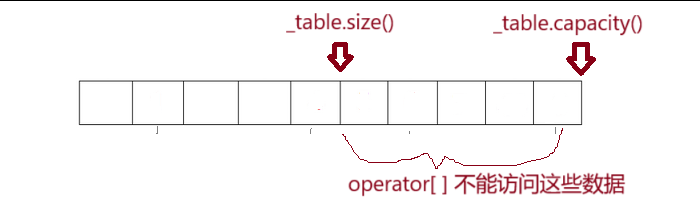
(2)int hashi = hf(key) % _table.size() 中模的是_table.size()

这是因为后续要通过 hashi 调用 _table的 operator[ ] 函数，operator[ ] 函数会对相应下标进行检测，如果越界就会直接报错

为了避免越界访问，我们在初始化时，将size与capacity 的大小设为一致

复制代码 
	HashTable()
	{
		_n = 0;
		_table.resize(10);//调用hashData的默认构造
	}

(3)while循环中，根据哈希表中数据的状态以及键值的比较判断数据是否存在，

返回时需要显示类型转换，因为指针类型不同(HashData<const K,V>*、HashData<K,V>*)

使用const修饰参数K是为了防止外界修改键值
(4)从后往前找，最后一个元素的下一个位置就是首元素位置，处理方法：

复制代码 
++hashi;
hashi %= _table.size();

1.3 insert函数

复制代码 
bool insert(const pair<K, V>& kv)
{
	if (find(kv.first))
		return false;
	//扩容逻辑：哈希表不能太满，太满会使查找、插入的效率下降
	
	//插入
	
	return true;
}

如果哈希表中已经有了该数据，就不再存储

插入

复制代码 
//插入
HashFunc hf;
int hashi = hf(kv.first) % _table.size();
//可能存在哈希冲突，向后寻找空或被删除的位置
while (_table[hashi]._state == EXIST)
{
	++hashi;
	hashi %= _table.size();//从后往前找
}
//修改状态，改值
_table[hashi]._state = EXIST;
_table[hashi]._kv = kv;
++_n;

return true;

(1)同样注意仿函数、取模的使用，潜在的哈希冲突问题通过线性探测找到空位置

(2)找到空位置后，修改该位置的元素及其状态

(2)最后注意 ++_n

扩容

复制代码 
			//扩容逻辑：哈希表不能太满，太满会使查找、插入的效率下降
			if ((double)_n / _table.size() >= 0.7)
			{
				int newSize = _table.size() * 2;
				//不能将原表直接扩容，因为
				//扩容可能会导致值存放的位置发生改变
				HashTable<K, V> newHt;
				newHt._table.resize(newSize);
				//复用insert函数
				for(int i = 0; i < _table.size(); ++i)
				{
					if(_table[i]._state == EXIST)
						newHt.insert(_table[i]._kv);
				}
				//两个vector进行交换
				_table.swap(newHt._table);
			}

(1)当载荷因子大于等于0.7时就扩容，判断条件注意类型转换

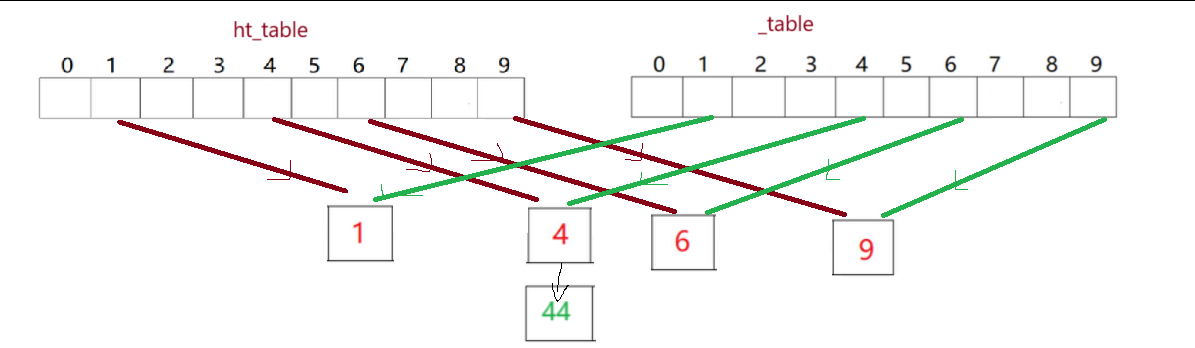
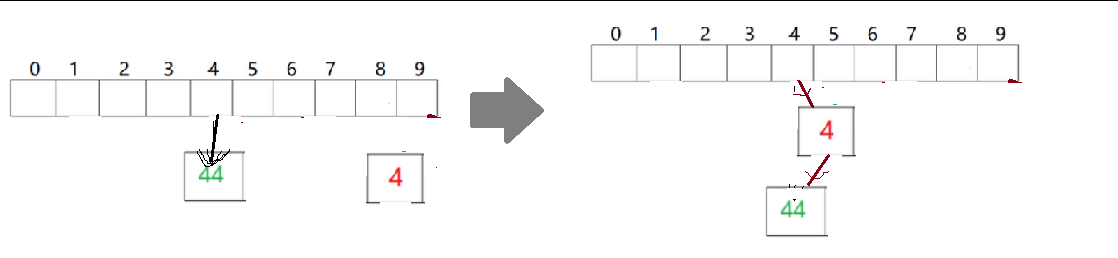
(2)不能 _table.resize(newSize); 进行扩容操作，这是因为

扩容可能会导致原来冲突的哈希值不冲突，原来不冲突的哈希值冲突，所以需要重新计算

(3)解决方法：

建立一张新的哈希表，遍历旧表，复用insert函数完成新表的插入，最后完成表的交换即可

1.4 erase函数

复制代码 
bool erase(const K& key)
{
    auto ret = find(key);
    if (!ret)
	    return false;
    else
    {
	    ret->_state = DELETE;
	    --_n;
	    return true;
    }
}

复用find函数，找到该元素后，修改元素状态和哈希表的有效数据个数

程序结束会自动调用HashData的析构函数清理资源

2.开散列实现

使用除留余数法计算哈希地址，链地址法解决哈希冲突

2.1前提准备

复制代码 
namespace hash_bucket
{
	template<class K, class V>
	struct HashNode
	{
		pair<K, V> _kv;
		HashNode<K, V>* _next;
		HashNode(const pair<K, V>& kv)
			:_kv(kv), _next(nullptr)
		{}
	};

	template<class K, class V, class HashFunc = DefaultHashFunc<K>>
	class HashTable
	{
		typedef HashNode<K, V> Node;
    public:
        
	private:
		vector<Node*> _table;
		size_t _n;
	};
}

(1)对于每一个哈希桶，使用的是单链表存储数据， HashNode就是数据节点

(2)这里仍需仿函数来完成字符串的整型转换操作

(3)_table 存储的就是每一个单链表的头节点，_n指的是有效数据的个数

(4)HashTable完成数据的增删查改工作

2.2 默认成员函数

  • 构造函数

    HashTable()
    {
    _n = 0;
    _table.resize(10, nullptr);//这里不会去调用HashNode的构造函数
    }

  • 析构函数

    ~HashTable()
    {
    for (int i = 0; i < _table.size(); ++i)
    {
    Node* cur = _table[i];
    while (cur)
    {
    Node* next = cur->_next;
    delete cur;
    cur = next;
    }
    _table[i] = nullptr;
    }
    }

析构函数的思路就是，从哈希表的第一个有效位置(指针不为空)开始，依次清理节点

因为节点 是我们手动创造的，需要我们手动释放，前面的闭散列实现方法中我们并没有手动创建资源

  • 拷贝构造函数

    HashTable(const HashTable<K, V>& ht)
    {
    _n = ht._n;
    _table.resize(ht._table.size());
    for (int i = 0; i < ht._table.size(); ++i)
    {
    Node* cur = ht._table[i];
    while (cur)
    {
    Node* newnode = new Node(cur->_kv);
    newnode->_next = _table[i];
    _table[i] = newnode;

    复制代码 
      		cur = cur->_next;
  	}
  }

    }

拷贝构造的重点是防止浅拷贝（不同哈希表指向相同的节点，导致最终资源二次释放）

拷贝构造的思路同样是遍历旧表，创建新节点存储对应的数据

注意新表的有效数据个数和大小与旧表一致

  • 赋值重载函数

    HashTable<K, V>& operator=(HashTable<K, V> ht)
    {
    _n = ht._n;
    _table.swap(ht._table);

    复制代码 
      return *this;

    }

形参 ht 完成对传入哈希表的深拷贝，这里只需要交换 _table ，修改有效值个数即可

2.3 find

复制代码 
HashNode<const K, V>* find(const K& key)
{
	HashFunc hf;
	int hashi = hf(key) % _table.size();
	Node* cur = _table[hashi];
	while (cur)
	{
		if (cur->_kv.first == key)
			return (HashNode<const K, V>*)cur;//指针类型不匹配需要显示转换

		cur = cur->_next;
	}

	return nullptr;
}

(1)对于仿函数、取模、类型转换的解释参考 闭散列实现的find函数

(2)开散列中，查找的思路是，通过取模找到对应的哈希地址，然后遍历链表进行查找

2.4 insert函数

复制代码 
bool insert(const pair<K, V>& kv)
{
	//去重
	if (find(kv.first))
		return false;

	//扩容：尽量使每一个桶只有一个数据，这样效率就非常高了

	//插入
	
	return true;
}

哈希表中有相同值就不再进行插入

插入

复制代码 
//插入
HashFunc hf;
int hashi = hf(kv.first) % _table.size();
Node* newnode = new Node(kv);
//头插
newnode->_next = _table[hashi];
_table[hashi] = newnode;
++_n;

对于仿函数、取模、的解释参考 闭散列实现的find函数

这里的插入方式实际上是单链表的插入方式：

对于单链表，头插的效率极高，实现方式：

当前节点成员单链表的头节点，当前节点的next指针指向原来的头节点

注意修改有效值_n

扩容

复制代码 
if (_n == _table.size())
{
	int newSize = _table.size() * 2;
	vector<Node*> newTable;
	newTable.resize(newSize);
	//遍历旧表，顺手牵羊
	for (int i = 0; i < _table.size(); ++i)
	{
		Node* cur = _table[i];
		while (cur)
		{
			Node* next = cur->_next;
			//映射关系要发生改变
			HashFunc hf;
			int hashi = hf(cur->_kv.first) % newSize;
			cur->_next = newTable[hashi];
			newTable[hashi] = cur;

			cur = next;
		}
		_table[i] = nullptr;
	}
	_table.swap(newTable);
}

(1)在元素个数刚好等于桶的个数时，可以给哈希表增容，这样查找的效率极高

(2)不能让旧表直接扩容，应该创建新表，重新映射插入数据后进行交换操作

(3)这里的重点是，我们不选择复用insert函数，因为旧表中的节点都是我们手动创建的，如果我们选择复用insert函数的话，我们需要在复用完成之后交换哈希表之前完成节点的资源释放，否则就会造成资源泄露，

创新方法：遍历旧表，从有效位置(节点指针不为空)开始，将节点"摘"到新的哈希表中(这里需要更新哈希地址同时注意头插及cur指针的移动)，最后完成交换操作即可

2.5 erase函数

复制代码 
bool erase(const K& key)
{
	HashFunc hf;
	int hashi = hf(key) % _table.size();
	Node* prev = nullptr;
	Node* cur = _table[hashi];
	while (cur)
	{
		if (cur->_kv.first == key)
		{
			if (!prev)
			{
				_table[hashi] = cur->_next;
			}
			else
			{
				prev->_next = cur->_next;
			}

			--_n;
			delete cur;
			return true;
		}
		//注意移动，不然内存泄漏
		prev = cur;
		cur = cur->_next;
	}

	return false;
}

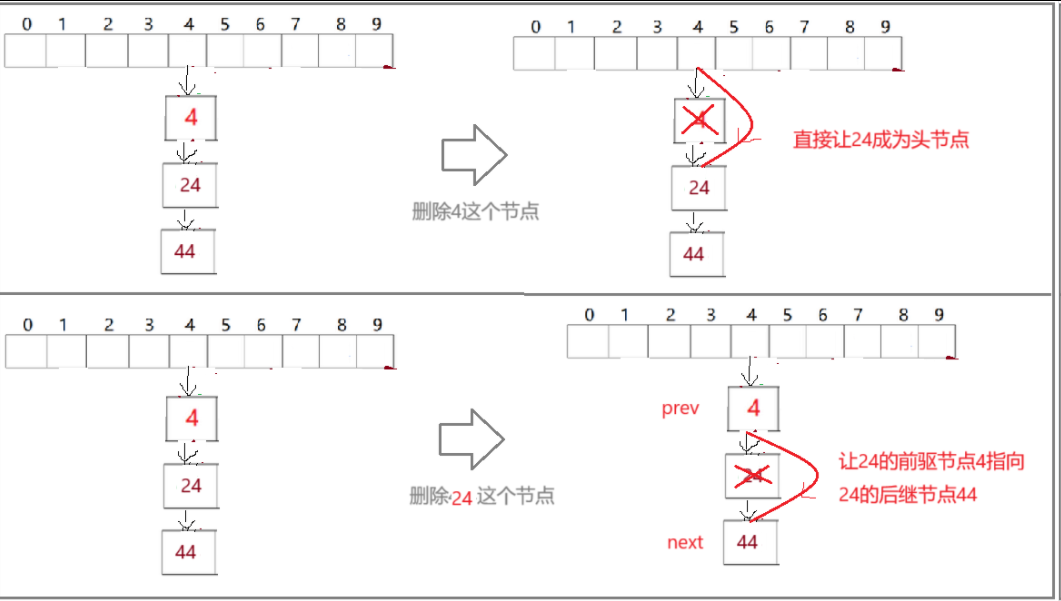
(1)这里不选择复用 find函数而只是复用查找的逻辑，是因为单链表的头删和中间删除有区别

2.6 Print函数

复制代码 
void Print()
{
	for (int i = 0; i < _table.size(); ++i)
	{
		printf("[%d]->", i);
		Node* cur = _table[i];
		while (cur)
		{
			cout << cur->_kv.first << ":" << cur->_kv.second << "->";
			cur = cur->_next;
		}
		printf("NULL\n");
	}
	cout << endl;
}

可以使用该函数打印开散列方法实现的哈希表

相关推荐
坚持编程的菜鸟1 小时前
LeetCode每日一题——重复的子字符串
数据结构·算法·leetcode
williamdsy6 小时前
【MoonBit初探】：从一个“陷阱”到深入理解数据结构*
数据结构·map·moonbit
无敌最俊朗@10 小时前
C++ 序列容器深度解析：vector、deque 与 list
开发语言·数据结构·数据库·c++·qt·list
Da Da 泓10 小时前
LinkedList模拟实现
java·开发语言·数据结构·学习·算法
jinmo_C++15 小时前
数据结构_ 二叉树线索化：从原理到手撕实现
数据结构
钮钴禄·爱因斯晨17 小时前
数据结构|图论：从数据结构到工程实践的核心引擎
c语言·数据结构·图论
向前阿、18 小时前
数据结构从入门到实战————栈
c语言·开发语言·数据结构·程序人生
洲覆19 小时前
Redis 64字节分界线与跳表实现原理
数据结构·数据库·redis·缓存
im_AMBER19 小时前
数据结构 02 线性表
数据结构·算法
-雷阵雨-19 小时前
数据结构——包装类&&泛型
java·开发语言·数据结构·intellij-idea
热门推荐
01UV安装并设置国内源02GitHub 镜像站点03UV 工具安装与国内镜像源配置指南04OpenSpeedy简介05在国行 macOS 下用 DeepSeek 补齐 Xcode 26 的 AI 能力：问题、原因与 mitmproxy 解决方案（含可用脚本与安装教程）06Spec-Kit 使用指南07阿里最新开源Wan2.2-Animate-14B 本地部署教程：统一双模态框架，MoE架构赋能电影级角色动画与替换08VsCode远程Copilot无法使用Claude Agent问题09KGG转MP3工具|非KGM文件|解密音频10Linux下V2Ray安装配置指南