"算法" 是计算机科学、数学及日常生活中都广泛存在的核心概念,本质是解决特定问题的、有限的、可重复执行的步骤集合 。它并非仅存在于代码或机器中,而是一种 "高效解决问题的逻辑框架"------ 小到每天规划通勤路线,大到人工智能识别图像,背后都依赖算法的支撑。
一、算法的核心定义与关键特征
要理解算法,需先明确其必须满足的 5 个核心特征,缺一不可:
- 有穷性:算法必须在 "有限步骤" 内结束。例如,计算 "1+2+3+...+100" 的算法(如高斯求和公式),无论用哪种方法,都能在固定步骤内得出结果;若步骤无限循环(如 "一直加 1 不停止"),则不构成算法。
- 确定性:每一步操作都必须 "唯一且明确",不存在歧义。例如,"将数字 x 乘以 2" 是确定的,但 "随便处理一下 x" 因无明确规则,不属于算法步骤。
- 可行性:算法的每一步都能通过 "实际可执行的操作" 实现。例如,"让计算机计算 10^100" 是可行的(计算机可处理大整数),但 "让计算机瞬间遍历无限个数字" 则不可行。
- 输入:算法可以有 0 个或多个 "明确的初始数据"。例如,"计算圆的面积" 需要输入 "半径"(1 个输入);"输出'Hello'" 则不需要输入(0 个输入)。
- 输出:算法必须有 1 个或多个 "明确的结果"。若执行后无任何结果(如 "仅定义步骤但不输出答案"),则不满足算法的核心目的。
二、算法的常见分类(按应用场景)
算法根据解决的问题类型,可分为多个领域,以下是最典型的几类:
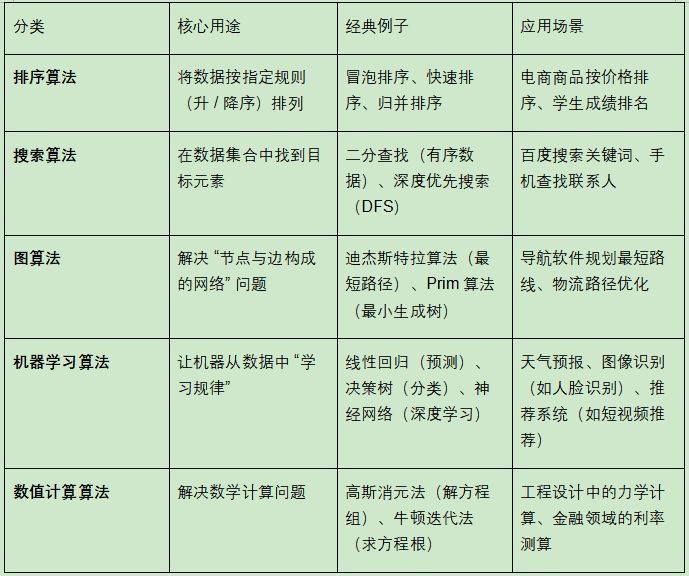
三、算法的 "好坏" 如何衡量?(效率指标)
同样的问题可能有多种算法(如 "排序 1000 个数字",可用冒泡排序或快速排序),但不同算法的 "效率" 天差地别,核心衡量指标有两个:
- 时间复杂度 :算法执行所需的 "时间成本",通常用 "步骤数随输入数据量增长的趋势" 表示(而非具体耗时,因耗时受硬件影响)。
- 例:排序 1000 个数字时,冒泡排序 的时间复杂度是 O (n²)(步骤数随数据量的平方增长,1000 个数据需约 100 万步);快速排序的时间复杂度是 O (n log n)(1000 个数据仅需约 1 万步)------ 显然快速排序更高效。
- 空间复杂度 :算法执行所需的 "内存成本",即存储中间数据占用的空间随输入数据量增长的趋势。
- 例:某些排序算法(如归并排序)需要额外存储一份数据副本(空间复杂度 O (n)),而原地排序算法(如堆排序)无需额外空间(空间复杂度 O (1)),更适合内存有限的设备(如嵌入式设备)。
四、算法的核心价值
算法是 "将抽象需求转化为可执行方案" 的桥梁:
- 对计算机而言:算法是代码的 "灵魂"------ 没有算法,代码只是无意义的指令;有了算法,计算机才能实现 "自动计算、识别、决策"。
- 对人类而言:算法是 "高效思维的工具"------ 它强迫我们将问题拆解为明确、可执行的步骤,避免混乱和遗漏,无论是解决数学问题还是规划人生,本质都是在设计 "属于自己的算法"。