金融量化指标--2Alpha 阿尔法

Alpha阿尔法的计算原理

添加图片注释，不超过 140 字（可选）

一、Alpha 的核心定义：它是什么？

在最基本的层面上，Alpha（α）是一个用于衡量投资策略超额回报的指标。它表示一项投资相对于市场整体表现（通常以某个基准指数，如沪深300、S&P 500等代表）所获得的超出或低于预期的收益。

通俗的理解：

市场平均收益 (Beta收益)：就像坐电梯，市场涨你大概率也涨，市场跌你大概率也跌。这部分收益是"被动"的，源于承担了系统风险。
超额收益 (Alpha收益)：就像在电梯里自己跳一跳，比别人更高。这部分收益是"主动"的，源于投资者的技能（如选股、择时、套利等），而非市场整体的恩赐。

因此，Alpha衡量的是基金经理或交易策略"跑赢大盘"的能力。

二、Alpha的计算与来源模型：资本资产定价模型 (CAPM)

Alpha的概念源于资本资产定价模型 (CAPM)。该模型描述了资产的预期收益率与其风险（Beta）之间的关系。

CAPM公式： E(Ri) = Rf + βi * [E(Rm) - Rf]

E(Ri)：资产 i 的预期收益率（根据模型计算出的"应得"回报）。
Rf：无风险利率（如国债收益率）。
βi (Beta)：资产 i 相对于市场的系统性风险系数。Beta=1表示波动与市场同步；>1更激进；<1更保守。
E(Rm)：市场的预期收益率。
$E(Rm) - Rf\]：市场风险溢价，即因承担市场风险而获得的额外补偿。$
Ri：资产 i 的实际实现收益率。
E(Ri)：由CAPM模型计算出的预期收益率。

所以： α = 实际收益 - (无风险收益 + Beta * 市场风险溢价)

结果解读：

α > 0：正Alpha。表示策略表现优异，成功获得了超越市场风险调整后的超额收益。这是所有主动管理者追求的目标。
α = 0：策略表现与市场一致，获得的收益恰好补偿了所承担的风险。买指数ETF的效果大致如此。
α < 0：负Alpha。表示策略表现不佳，即使考虑了风险因素，其收益也低于市场水平。

三、为什么Alpha如此重要？------意义与用途

衡量投资技能的核心指标： Alpha剥离了市场波动（Beta）带来的影响，直接拷问基金经理的真实选股和择时能力。一个持续产生正Alpha的基金经理被认为是有真本事的。
基金业绩评估和比较：投资者可以用Alpha来比较不同基金的表现。两只收益相同的基金，Alpha更高的那只意味着基金经理在更低的风险（或同样的风险下创造了更多收益）下取得了同样的成绩，显然更具吸引力。
量化策略的"圣杯"：在量化投资领域，开发和回测策略的终极目标就是寻找能持续产生显著正Alpha的因子或模型。Alpha是量化模型价值的直接体现。
资产定价的基准： Alpha帮助判断一项资产是否被错误定价。正Alpha可能意味着资产被低估，负Alpha则可能意味着被高估。

四、Alpha的进阶理解与局限性

虽然Alpha很强大，但它并非完美无缺，需要正确理解其局限性：

对基准的依赖性极强： Alpha的计算结果严重依赖于所选择的市场基准指数。如果用错了基准，Alpha就失去了意义。例如，评价一个创业板股票策略，如果用上证50作基准，可能会计算出巨大的正Alpha，但这显然是错误的。选择合适的基准是计算Alpha的前提。
依赖CAPM模型的假设： CAPM模型本身有其假设（如市场有效、投资者理性等），现实世界往往不完全符合这些假设。因此，Alpha可能包含了模型未捕捉到的其他风险因素。
多因子模型的演进：由于CAPM的单因子（市场因子）解释力有限，学术界和业界发展出了多因子模型（如Fama-French三因子、五因子模型）。在这些模型中，Alpha的含义变成了剥离了所有已知风险因子（如市值、估值、动量等）暴露后剩余的"纯净"超额收益。此时的Alpha更难获得，也更能体现真正的选股能力。 α = 实际收益 - (无风险收益 + β1*因子1溢价 + β2*因子2溢价 + ...)
统计显著性与可持续性：计算出的Alpha是否在统计上显著（例如，t-statistic > 2）？它是不是只是运气好（偶然性）的结果？一个策略短期内有正Alpha很容易，难的是长期、持续地产生显著的正Alpha。
数据挖掘陷阱：在量化领域，过度回测和优化（过拟合）可能会在历史数据上产生漂亮的Alpha，但这个Alpha在未来无法重现（"在样本内表现完美，在样本外表现糟糕"）。

五、Alpha在实战中的应用示例

假设：

无风险利率 Rf = 2%
市场基准收益率 Rm = 10%
某基金的实际收益率 Ri = 18%
该基金的Beta值 β = 1.2

步骤1：计算预期收益率 E(Ri) E(Ri) = 2% + 1.2 * (10% - 2%) = 2% + 1.2 * 8% = 2% + 9.6% = 11.6%

步骤2：计算Alpha α α = 18% - 11.6% = +6.4%

结论：该基金获得了6.4%的正Alpha。这意味着基金经理通过其出色的管理能力，带来了远超其承担风险（Beta=1.2）所应得回报的超额收益。

总结

特性	描述
本质	风险调整后的超额收益，衡量主动管理技能。
核心思想	将收益分解为市场带来的 (Beta) 和技能带来的 (Alpha) 两部分。
计算公式	α = 实际收益 - [无风险收益 + Beta * (市场收益 - 无风险收益)]
理想状态	显著且持续的正Alpha。
关键局限性	高度依赖基准选择；模型假设可能不成立；可能包含未知风险；需警惕数据挖掘和过拟合。
进阶应用	在多因子模型中，Alpha是剥离所有已知风险因子后的"纯净"收益，是更高阶的阿尔法。

总而言之，Alpha是金融世界里衡量"增值价值"的黄金标准。它迫使投资者超越简单的收益率比较，深入到风险调整后的绩效评估层面。无论是评价一只基金，还是开发一个量化策略，对Alpha的深刻理解和正确运用都是至关重要的。

下面是计算模型的输出结果

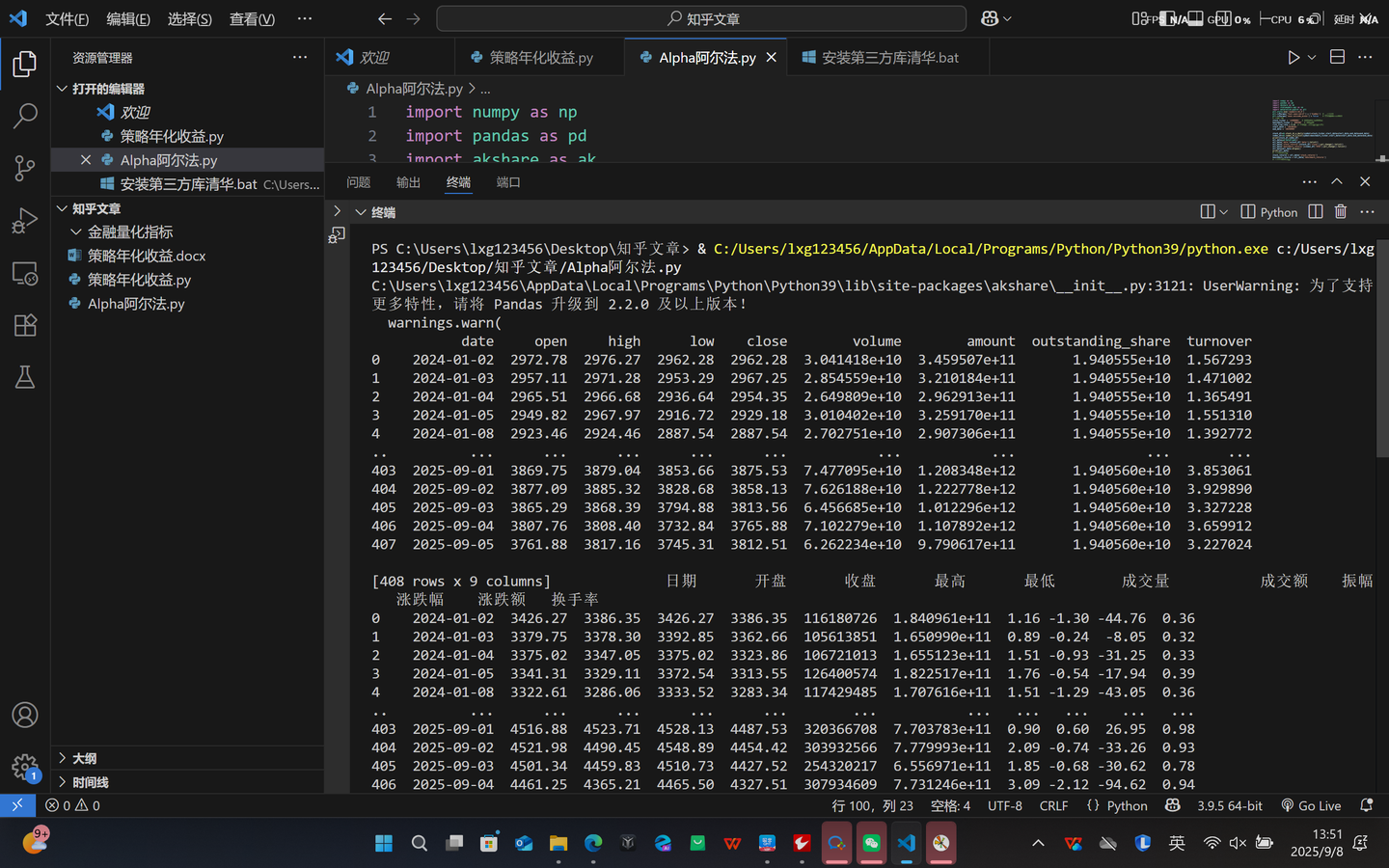
添加图片注释，不超过 140 字（可选）

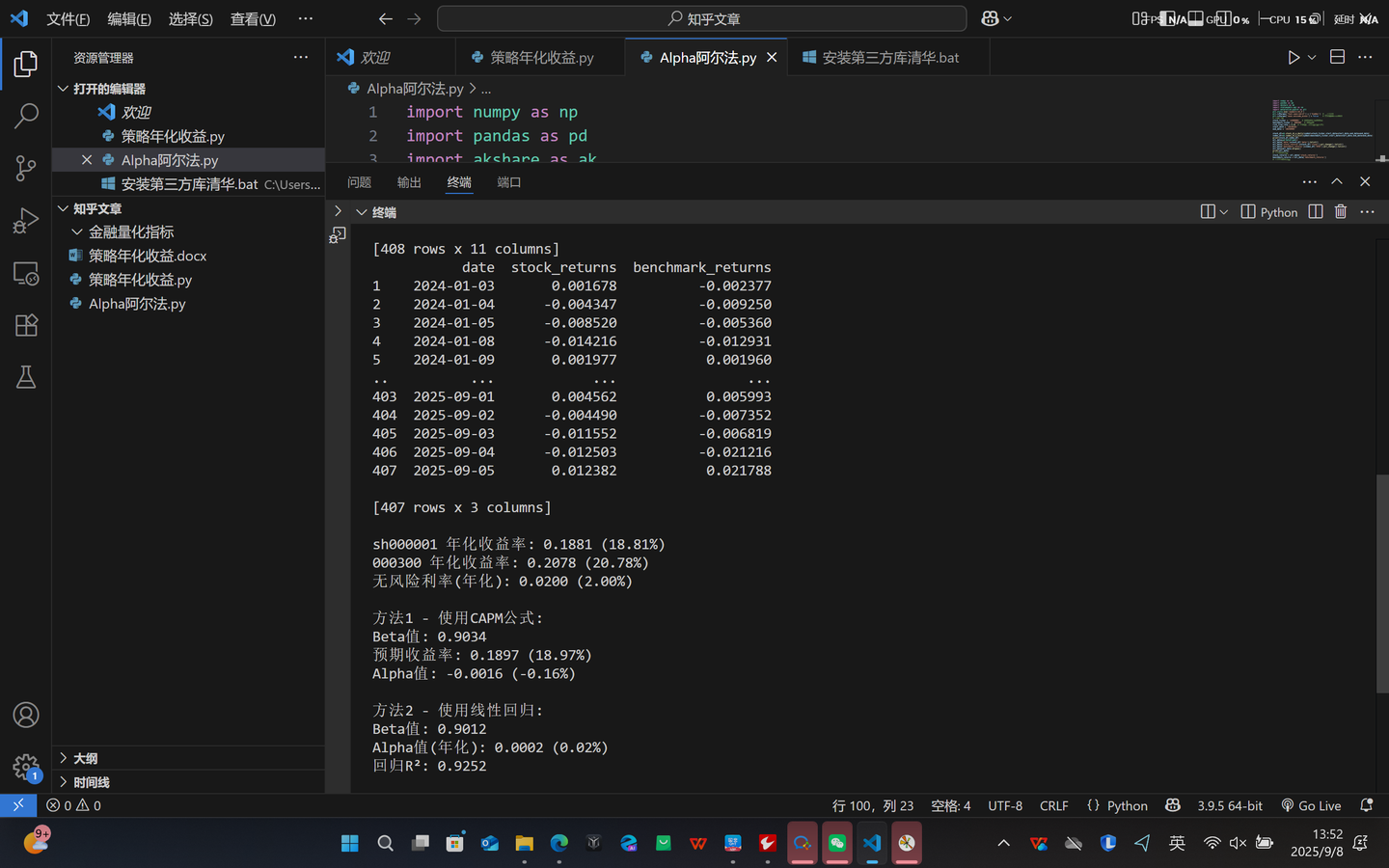
添加图片注释，不超过 140 字（可选）

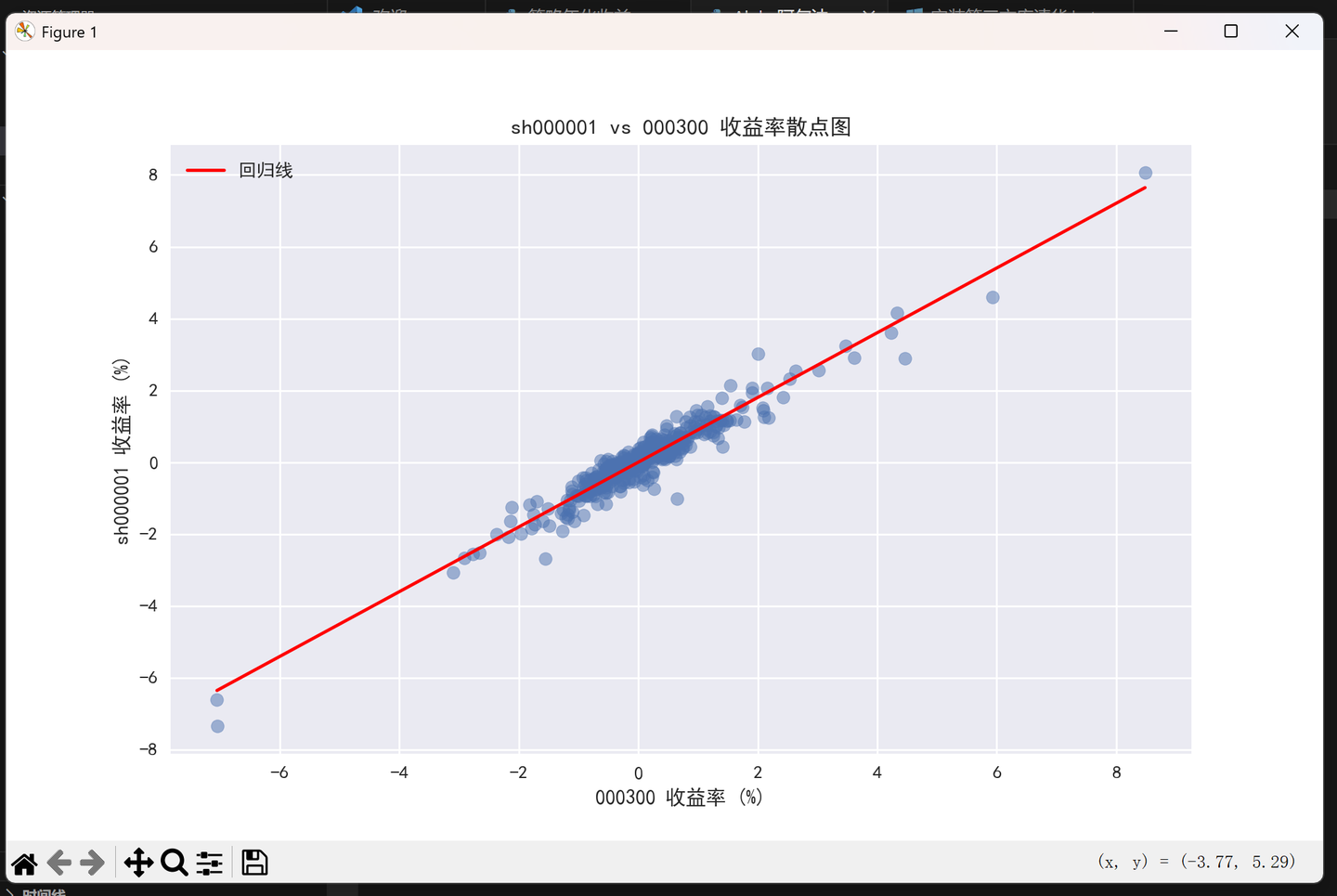
添加图片注释，不超过 140 字（可选）

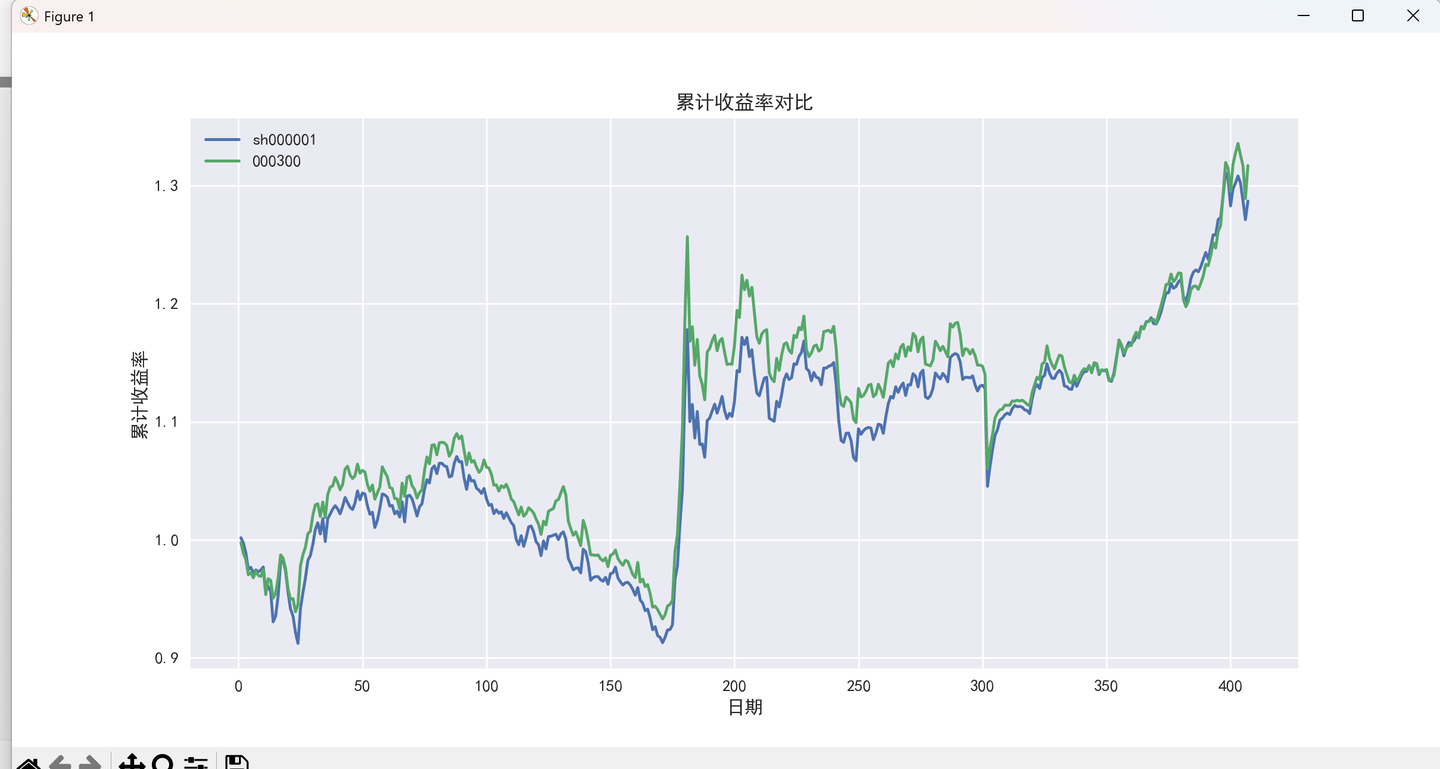
添加图片注释，不超过 140 字（可选）

计算源代码

python 复制代码

import numpy as np
import pandas as pd
import akshare as ak
import statsmodels.api as sm
import matplotlib.pyplot as plt
plt.style.use('seaborn-v0_8')
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题
# 设置参数
stock_ticker = 'sh000001'  # 投资组合/股票代码
benchmark_ticker = '000300'  # 300指数
risk_free_rate = 0.02  # 年化无风险利率(假设2%)
start_date = '20240101'
end_date = '20250905'

stock_df=ak.stock_zh_a_daily(symbol=stock_ticker,start_date=start_date,end_date=end_date)
index_df=ak.index_zh_a_hist(symbol=benchmark_ticker,start_date=start_date,end_date=end_date)
print(stock_df,index_df)
all_data=pd.DataFrame()
all_data['date']=stock_df['date'].tolist()
all_data['stock_returns']=stock_df['close'].pct_change().tolist()
all_data['benchmark_returns']=index_df['收盘'].pct_change().tolist()
all_data=all_data.dropna()
print(all_data)
# 计算日收益率
stock_returns = all_data['stock_returns']
benchmark_returns = all_data['benchmark_returns']
# 计算年化收益率
days_per_year = 252
stock_annual_return = (1 + stock_returns.mean()) ** days_per_year - 1
benchmark_annual_return = (1 + benchmark_returns.mean()) ** days_per_year - 1
risk_free_daily = (1 + risk_free_rate) ** (1/days_per_year) - 1

print(f"\n{stock_ticker} 年化收益率: {stock_annual_return:.4f} ({stock_annual_return*100:.2f}%)")
print(f"{benchmark_ticker} 年化收益率: {benchmark_annual_return:.4f} ({benchmark_annual_return*100:.2f}%)")
print(f"无风险利率(年化): {risk_free_rate:.4f} ({risk_free_rate*100:.2f}%)")

# 方法1: 使用CAPM公式计算Alpha
# 首先计算Beta值
covariance = np.cov(stock_returns, benchmark_returns)[0, 1]
benchmark_variance = np.var(benchmark_returns)
beta = covariance / benchmark_variance

# 计算Alpha
expected_return = risk_free_rate + beta * (benchmark_annual_return - risk_free_rate)
alpha = stock_annual_return - expected_return

print(f"\n方法1 - 使用CAPM公式:")
print(f"Beta值: {beta:.4f}")
print(f"预期收益率: {expected_return:.4f} ({expected_return*100:.2f}%)")
print(f"Alpha值: {alpha:.4f} ({alpha*100:.2f}%)")

# 方法2: 使用线性回归计算Alpha和Beta
# 添加常数项(Alpha)到自变量
X = sm.add_constant(benchmark_returns - risk_free_daily)
y = stock_returns - risk_free_daily

# 执行回归
model = sm.OLS(y, X).fit()
alpha_reg = model.params[0] * days_per_year  # 将日Alpha年化
beta_reg = model.params[1]

print(f"\n方法2 - 使用线性回归:")
print(f"Beta值: {beta_reg:.4f}")
print(f"Alpha值(年化): {alpha_reg:.4f} ({alpha_reg*100:.2f}%)")
print(f"回归R²: {model.rsquared:.4f}")

# 绘制散点图和回归线
plt.figure(figsize=(10, 6))
plt.scatter(benchmark_returns * 100, stock_returns * 100, alpha=0.5)
plt.xlabel(f'{benchmark_ticker} 收益率 (%)')
plt.ylabel(f'{stock_ticker} 收益率 (%)')
plt.title(f'{stock_ticker} vs {benchmark_ticker} 收益率散点图')

# 添加回归线
x_range = np.linspace(benchmark_returns.min() * 100, benchmark_returns.max() * 100, 100)
plt.plot(x_range, (risk_free_daily + model.params[0] + model.params[1] * (x_range/100 - risk_free_daily)) * 100, 
         color='red', label='回归线')

plt.legend()
plt.grid(True)
plt.show()

# 绘制累计收益率对比
cumulative_stock = (1 + stock_returns).cumprod()
cumulative_benchmark = (1 + benchmark_returns).cumprod()

plt.figure(figsize=(12, 6))
plt.plot(cumulative_stock, label=stock_ticker)
plt.plot(cumulative_benchmark, label=benchmark_ticker)
plt.title('累计收益率对比')
plt.xlabel('日期')
plt.ylabel('累计收益率')
plt.legend()
plt.grid(True)
plt.show()

# 输出回归摘要
print("\n回归模型摘要:")
print(model.summary())