CNNMNIST

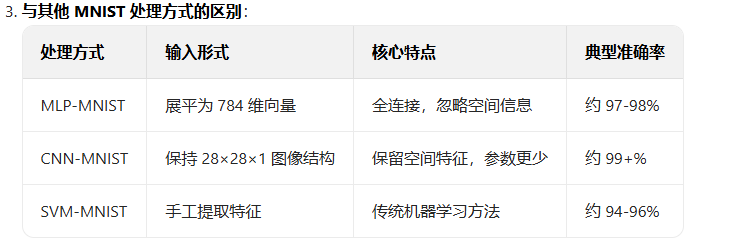
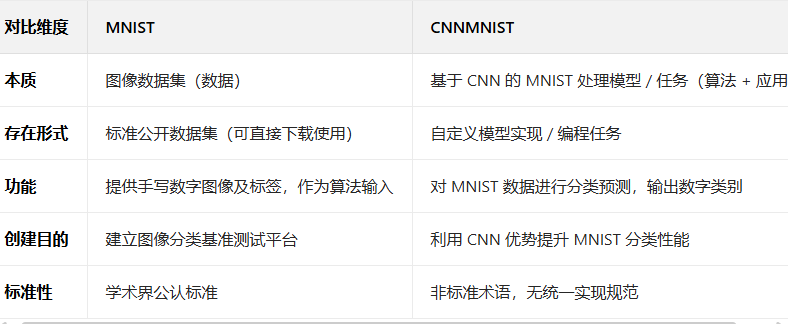
CNNMNIST 通常指用卷积神经网络 (CNN) 处理 MNIST 数据集的任务 / 模型

代码

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt

# 设置随机种子以确保结果可复现
torch.manual_seed(42)

# 定义数据转换
transform = transforms.Compose([
    transforms.ToTensor(),  # 转换为张量
    transforms.Normalize((0.1307,), (0.3081,))  # 标准化，使用MNIST数据集的均值和标准差
])

# 加载MNIST数据集
def load_data(batch_size=64):
    print("正在加载MNIST数据集...")
    # 训练数据集
    train_dataset = datasets.MNIST(
        root='./data',
        train=True,
        download=True,
        transform=transform
    )
    
    # 测试数据集
    test_dataset = datasets.MNIST(
        root='./data',
        train=False,
        download=True,
        transform=transform
    )
    
    # 创建数据加载器
    train_loader = torch.utils.data.DataLoader(
        train_dataset,
        batch_size=batch_size,
        shuffle=True
    )
    
    test_loader = torch.utils.data.DataLoader(
        test_dataset,
        batch_size=batch_size,
        shuffle=False
    )
    
    print(f"数据集加载完成: 训练集{len(train_dataset)}张图像, 测试集{len(test_dataset)}张图像")
    return train_loader, test_loader

# 定义卷积神经网络模型
class CNNMNIST(nn.Module):
    def __init__(self):
        super(CNNMNIST, self).__init__()
        # 第一个卷积层：输入通道1，输出通道16，卷积核大小3x3，步长1， padding=1
        self.conv1 = nn.Conv2d(1, 16, kernel_size=3, stride=1, padding=1)
        # 第二个卷积层：输入通道16，输出通道32，卷积核大小3x3，步长1， padding=1
        self.conv2 = nn.Conv2d(16, 32, kernel_size=3, stride=1, padding=1)
        # 最大池化层：池化核大小2x2，步长2
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
        
        # 三个全连接层
        # 卷积后的特征图大小: (28 -> 14 -> 7) 经过两次池化
        # 输入特征数: 32 * 7 * 7 = 1568
        self.fc1 = nn.Linear(32 * 7 * 7, 128)
        self.fc2 = nn.Linear(128, 64)
        self.fc3 = nn.Linear(64, 10)
        
        # Dropout层防止过拟合
        self.dropout = nn.Dropout(0.25)
    
    def forward(self, x):
        # 第一个卷积层 + ReLU激活 + 池化
        x = self.pool(F.relu(self.conv1(x)))
        # 第二个卷积层 + ReLU激活 + 池化
        x = self.pool(F.relu(self.conv2(x)))
        # 展平特征图
        x = x.view(-1, 32 * 7 * 7)
        # 第一个全连接层 + ReLU激活
        x = F.relu(self.fc1(x))
        x = self.dropout(x)
        # 第二个全连接层 + ReLU激活
        x = F.relu(self.fc2(x))
        x = self.dropout(x)
        # 第三个全连接层（输出层）
        x = self.fc3(x)
        return x

# 训练模型
def train_model(model, train_loader, epochs=5, learning_rate=0.001):
    # 定义损失函数
    criterion = nn.CrossEntropyLoss()
    # 定义优化器
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)
    
    # 确保模型在训练模式
    model.train()
    
    train_losses = []
    train_accuracies = []
    
    print(f"开始训练模型，共{epochs}个epoch")
    
    for epoch in range(epochs):
        running_loss = 0.0
        correct = 0
        total = 0
        
        for i, (images, labels) in enumerate(train_loader):
            # 梯度清零
            optimizer.zero_grad()
            
            # 前向传播
            outputs = model(images)
            
            # 计算损失
            loss = criterion(outputs, labels)
            
            # 反向传播
            loss.backward()
            
            # 更新参数
            optimizer.step()
            
            # 统计损失
            running_loss += loss.item()
            
            # 计算准确率
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
            
            # 每100个batch打印一次训练状态
            if (i + 1) % 100 == 0:
                print(f'Epoch [{epoch + 1}/{epochs}], Step [{i + 1}/{len(train_loader)}], '\
                      f'Loss: {running_loss / (i + 1):.4f}, Accuracy: {100 * correct / total:.2f}%')
        
        # 记录每个epoch的平均损失和准确率
        epoch_loss = running_loss / len(train_loader)
        epoch_acc = 100 * correct / total
        train_losses.append(epoch_loss)
        train_accuracies.append(epoch_acc)
        
        print(f'Epoch [{epoch + 1}/{epochs}] 完成 - 平均损失: {epoch_loss:.4f}, 准确率: {epoch_acc:.2f}%')
    
    print("训练完成！")
    return train_losses, train_accuracies

# 测试模型
def test_model(model, test_loader):
    # 设置模型为评估模式
    model.eval()
    
    correct = 0
    total = 0
    
    # 不计算梯度
    with torch.no_grad():
        for images, labels in test_loader:
            # 前向传播
            outputs = model(images)
            
            # 预测结果
            _, predicted = torch.max(outputs.data, 1)
            
            # 统计
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    
    # 计算准确率
    accuracy = 100 * correct / total
    print(f'测试集准确率: {accuracy:.2f}%')
    return accuracy

# 保存模型
def save_model(model, filepath='mnist_cnn_model.pth'):
    torch.save(model.state_dict(), filepath)
    print(f"模型已保存到 {filepath}")

# 可视化训练结果
def visualize_training(train_losses, train_accuracies, test_accuracy):
    plt.figure(figsize=(12, 5))
    
    # 绘制损失曲线
    plt.subplot(1, 2, 1)
    plt.plot(range(1, len(train_losses) + 1), train_losses, 'b-', marker='o')
    plt.title('Training Loss')
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.grid(True)
    
    # 绘制准确率曲线
    plt.subplot(1, 2, 2)
    plt.plot(range(1, len(train_accuracies) + 1), train_accuracies, 'r-', marker='o')
    plt.axhline(y=test_accuracy, color='g', linestyle='--', label=f'Test Accuracy: {test_accuracy:.2f}%')
    plt.title('Training Accuracy')
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy (%)')
    plt.legend()
    plt.grid(True)
    
    plt.tight_layout()
    plt.show()

# 可视化预测结果
def visualize_predictions(model, test_loader):
    model.eval()
    # 获取一批测试数据
    images, labels = next(iter(test_loader))
    
    # 预测
    with torch.no_grad():
        outputs = model(images)
        _, predictions = torch.max(outputs, 1)
    
    # 显示一些测试图像及其预测结果
    plt.figure(figsize=(10, 4))
    for i in range(min(5, len(images))):
        plt.subplot(1, 5, i + 1)
        # 转换为numpy数组并恢复原始形状
        img = images[i].numpy().squeeze()
        plt.imshow(img, cmap='gray')
        plt.title(f'Pred: {predictions[i]}\nActual: {labels[i]}')
        plt.axis('off')
    plt.tight_layout()
    plt.show()

# 主函数
def main():
    # 设置训练参数
    batch_size = 64
    epochs = 5
    learning_rate = 0.001
    model_save_path = 'mnist_cnn_model.pth'
    
    # 加载数据
    train_loader, test_loader = load_data(batch_size)
    
    # 创建模型实例
    print("创建卷积神经网络模型...")
    model = CNNMNIST()
    print(model)
    
    # 训练模型
    train_losses, train_accuracies = train_model(model, train_loader, epochs, learning_rate)
    
    # 测试模型
    test_accuracy = test_model(model, test_loader)
    
    # 保存模型
    save_model(model, model_save_path)
    
    # 可视化训练结果
    print("显示训练结果图表...")
    visualize_training(train_losses, train_accuracies, test_accuracy)
    
    # 可视化预测结果
    print("显示预测结果示例...")
    visualize_predictions(model, test_loader)

if __name__ == "__main__":
    main()

---

CNNMNIST

通常指使用卷积神经网络 (CNN) 对 MNIST 数据集进行分类的任务或模型实现

• 针对 MNIST 图像的空间结构特点，采用 CNN 的局部连接、权值共享、池化操作等特性
• 典型架构：输入层 (28×28×1)→卷积层→池化层→全连接层→输出层 (10 分类)
• 经典实现：LeNet-5（最早用于 MNIST 的 CNN 架构，1998 年提出

self.conv1 = nn.Conv2d(1, 16, kernel_size=3, stride=1, padding=1)

out_channels的输出通道数是16，就意味着要有16个卷积和

特征图的空间尺寸公式： (W - F + 2P) / S + 1

|--------|-------------------|-------------------|------------------------------|
| 符号 | 含义 | 原代码 conv1 的取值 | 补充说明 |
| W | 输入特征图的宽度 / 高度 | 28 | MNIST 原始图像尺寸是 28×28，单通道 |
| F | 卷积核（kernel）的尺寸 | 3 | 原代码kernel_size=3，即 3×3 卷积核 |
| P | 边界填充（padding）的像素数 | 1 | 原代码padding=1，图像周围补 1 圈 0 |
| S | 卷积核的滑动步长（stride） | 1 | 原代码stride=1，每次滑动 1 个像素 |
| 输出 | 卷积后特征图的宽度 / 高度 | 28 | 代入公式计算结果，和输入尺寸一致 |

二、公式的核心作用：精准计算卷积后的特征图大小

为什么需要这个公式？------ 卷积层会改变特征图的空间尺寸（宽 / 高），而后续层（比如池化层、全连接层）的输入依赖这个尺寸，一旦算错，就会报 "维度不匹配" 错误。

用原代码 conv1 验证公式：输入 W=28，F=3，P=1，S=1代入公式：(28 - 3 + 2×1) / 1 + 1 = (28-3+2) +1 = 27 +1 = 28结果和预期一致：conv1 后特征图尺寸还是 28×28，没有缩小，这也是原代码设计padding=1的目的 ------ 避免边缘信息丢失，同时保持尺寸稳定。

问题

针对1通道数 3*3的卷积核 那也就是这个卷积核有9个参数， 该输出特征图的尺寸是多少？

假设还是 MNIST 的输入（28×28），卷积核参数 kernel_size=3, stride=1, padding=1（和原代码一致），代入公式：H_out = W_out = (28 - 3 + 2×1)/1 + 1 = 28

所以这层卷积的最终输出是：(batch_size, 16, 28, 28) → 每个批次有 16 张 28×28 的特征图（16 种不同的基础特征）。

16 个卷积核总共要学多少参数？

单个 3×3 卷积核有 9 个参数（完全正确！3×3=9），但实际每个卷积核还要加 1 个「偏置项」（bias，用于调整特征图的整体亮度，让模型更灵活），所以：

1. 单个卷积核的参数数

= 卷积核尺寸（3×3）× 输入通道数（1） + 偏置项（1）= 3×3×1 + 1 = 10 个参数

2. 16 个卷积核的总参数数

= 单个卷积核参数数 × 输出通道数（16）= 10 × 16 = 160 个参数