上一章: 机器学习03------线性模型
下一章: 机器学习05------多分类学习与类别不平衡
机器学习实战项目: 【从 0 到 1 落地】机器学习实操项目目录:覆盖入门到进阶,大学生就业 / 竞赛必备
文章目录
一、决策树的基本流程
决策树是一种基于"分而治之"思想的监督学习模型,通过递归划分样本构建树状结构,每个节点对应一个属性测试,叶节点对应决策结果。
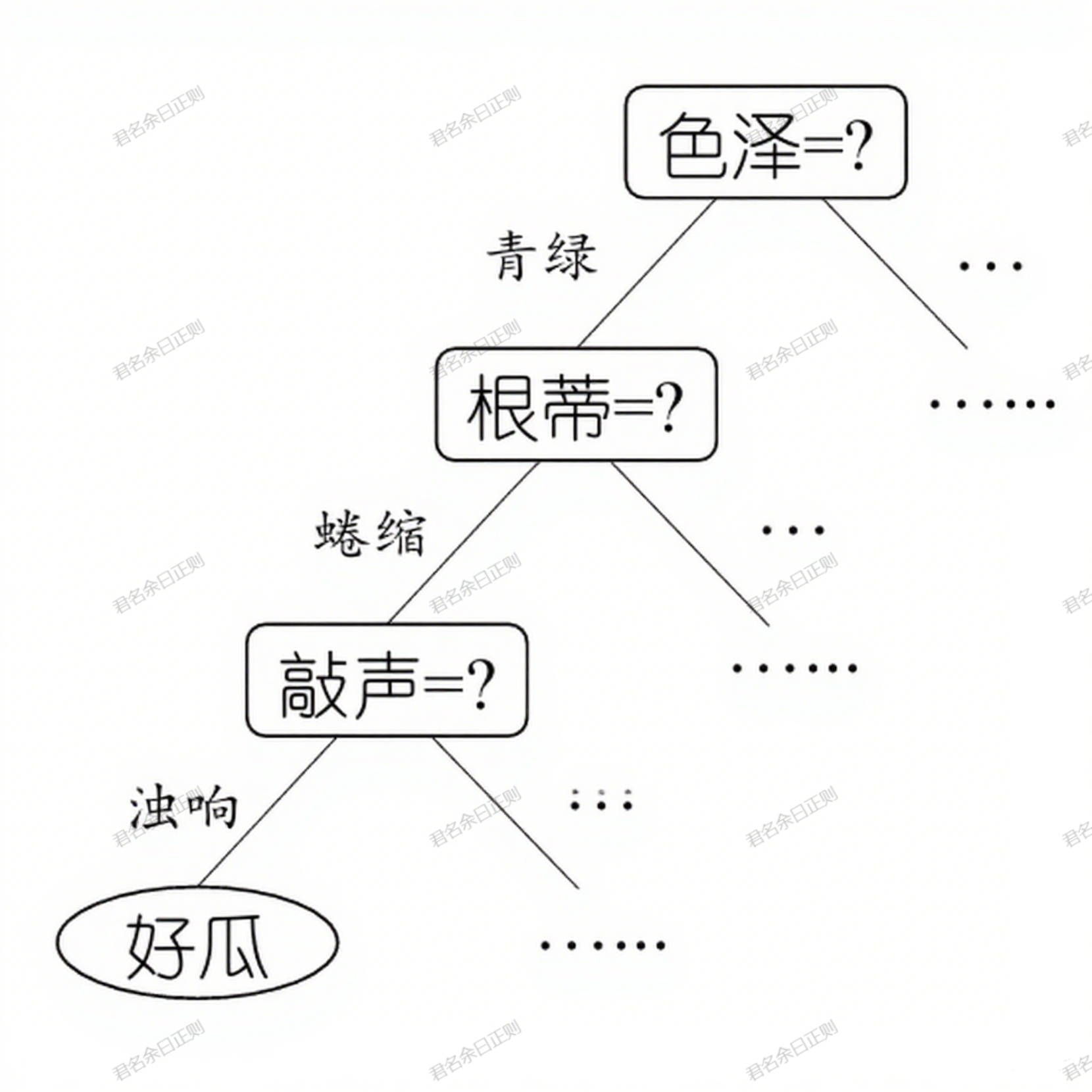
(一)核心原理
- 决策过程:从根节点开始,对样本的某个属性进行测试,根据测试结果进入相应子节点,重复此过程直至叶节点,得到决策结果。从根节点到叶节点的路径对应一个判定规则序列。
- 终止条件:当满足以下任一条件时,停止划分并将当前节点标记为叶节点:
- 当前节点的所有样本属于同一类别;
- 属性集为空,或所有样本在剩余属性上取值相同(此时标记为样本数最多的类别);
- 当前节点包含的样本集为空(此时标记为父节点样本数最多的类别)。

(二)生成算法
- 输入:训练集 D = { ( x 1 , y 1 ) , . . . , ( x m , y m ) } D=\{(x_1,y_1),..., (x_m,y_m)\} D={(x1,y1),...,(xm,ym)}和属性集 A = { a 1 , . . . , a d } A=\{a_1,...,a_d\} A={a1,...,ad};
- 递归过程(函数TreeGenerate(D,A)):
- 生成当前节点,检查是否满足终止条件,若满足则标记为叶节点并返回;
- 否则从属性集A中选择最优划分属性 a ∗ a^* a∗;
- 对 a ∗ a^* a∗的每个取值 a v ∗ a^*_v av∗,生成子节点,将D中取值为 a v ∗ a^*_v av∗的样本子集 D v D_v Dv传入子节点,递归调用TreeGenerate ( D v , A − { a ∗ } ) (D_v, A-\{a^*\}) (Dv,A−{a∗})。
二、划分选择(最优属性的判定)
决策树学习的关键是选择最优划分属性,目标是使划分后各子节点的样本纯度尽可能高。经典方法包括信息增益、增益率和基尼指数。
(一)信息增益(ID3算法)
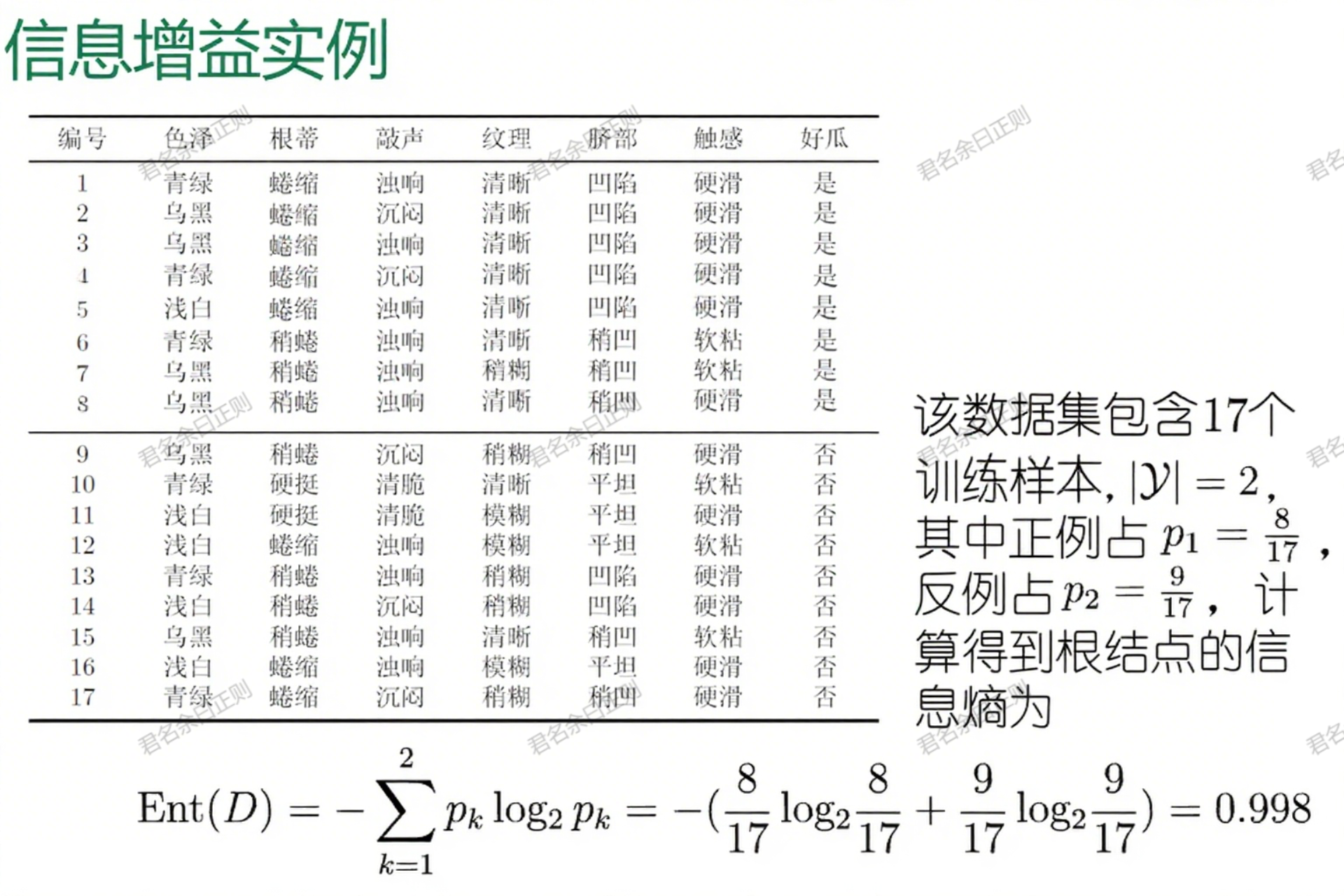
- 信息熵 :衡量样本集纯度的指标,对于包含 ∣ Y ∣ |\mathcal{Y}| ∣Y∣类样本的集合D,第k类样本占比为 p k p_k pk,则信息熵为:
E n t ( D ) = − ∑ k = 1 ∣ Y ∣ p k log 2 p k Ent(D)=-\sum_{k=1}^{|\mathcal{Y}|} p_k \log_2 p_k Ent(D)=−k=1∑∣Y∣pklog2pk
Ent(D)值越小,样本集纯度越高(如全为同一类时Ent(D)=0)。 - 信息增益 :属性a对D的划分所带来的信息熵减少量,计算公式为:
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^V \frac{|D^v|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
其中 D v D^v Dv是D中在属性a上取值为 a v a^v av的样本子集,V是属性a的取值数。信息增益越大,说明该属性划分后样本纯度提升越明显。 - 示例:在"好瓜"识别中,属性"纹理"的信息增益(0.381)高于其他属性,因此被选为根节点的划分属性。
- 局限 :对取值数目多的属性有偏好(如"编号"这类唯一标识属性,信息增益通常极高,但无泛化意义)。


(二)增益率(C4.5算法)
为修正信息增益的偏好,引入增益率,定义为:
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} Gain_ratio(D,a)=IV(a)Gain(D,a)
其中 I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ log 2 ∣ D v ∣ ∣ D ∣ IV(a)=-\sum_{v=1}^V \frac{|D^v|}{|D|}\log_2 \frac{|D^v|}{|D|} IV(a)=−∑v=1V∣D∣∣Dv∣log2∣D∣∣Dv∣为属性a的"固有值",取值越多的属性,IV(a)越大,从而抑制高取值属性的优势。
- 启发式策略:C4.5算法先筛选出信息增益高于平均水平的属性,再从中选择增益率最高的,平衡偏好问题。
(三)基尼指数(CART算法)
基尼指数衡量从样本集中随机抽取两个样本,其类别标记不同的概率,计算公式为:
G i n i ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ Y ∣ p k 2 Gini(D)=\sum_{k=1}^{|\mathcal{Y}|}\sum_{k'\neq k} p_k p_{k'}=1-\sum_{k=1}^{|\mathcal{Y}|} p_k^2 Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=1−k=1∑∣Y∣pk2
Gini(D)越小,样本集纯度越高。属性a的基尼指数为划分后各子节点基尼指数的加权和,选择基尼指数最小的属性作为划分属性。
三、剪枝处理(避免过拟合)
剪枝是决策树对抗过拟合的核心手段,通过移除冗余分支,提升模型泛化能力。分为预剪枝和后剪枝。
(一)预剪枝
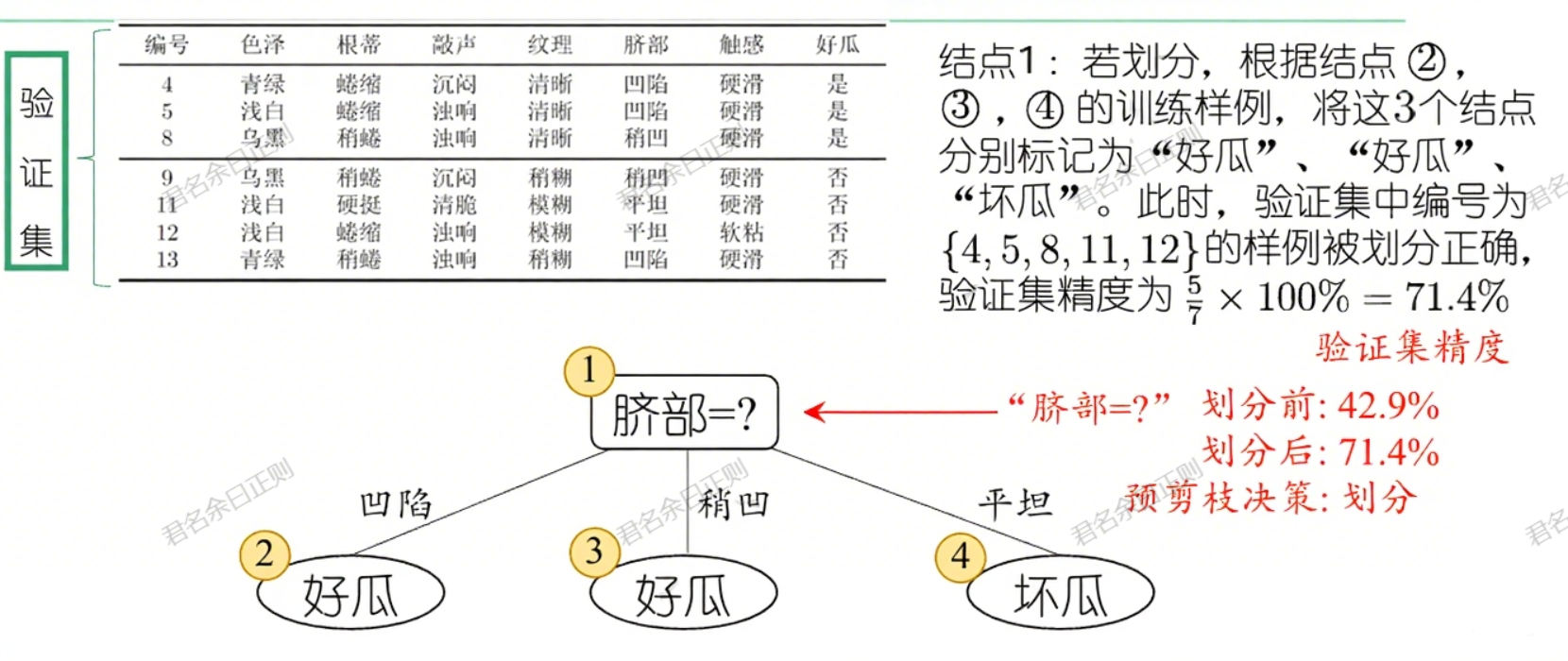
- 策略:在决策树生成过程中,对每个节点先判断划分是否能提升泛化性能(通过验证集精度评估),若不能则停止划分,将当前节点标记为叶节点。
- 示例:对"好瓜"数据集的根节点,若不划分(标记为"好瓜"),验证集精度为42.9%;若用"脐部"划分,精度提升至71.4%,则进行划分;后续子节点若划分不能提升精度,则停止。
- 优缺点 :
- 优点:减少训练和测试时间开销;
- 缺点:可能因"贪心"策略错过后续有效划分,导致欠拟合。
(二)后剪枝
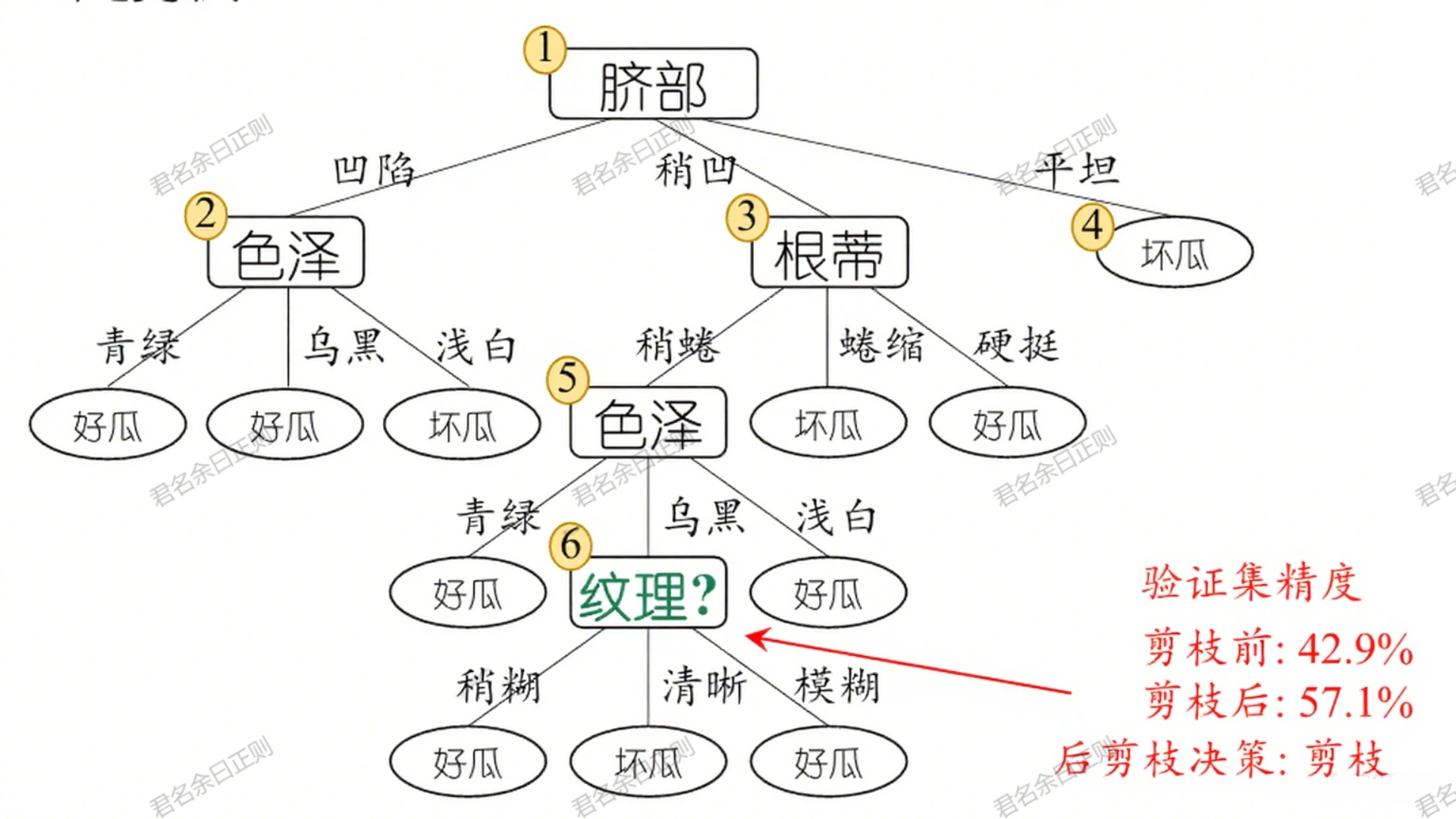
- 策略:先生成完整决策树,再自底向上考察非叶节点,若将其子树替换为叶节点能提升泛化性能,则剪枝。
- 示例:对完整决策树的子节点,若替换为叶节点后验证集精度从42.9%提升至更高,则剪枝;最终保留更多有效分支。
- 优缺点 :
- 优点:泛化性能通常优于预剪枝,保留更多有效分支;
- 缺点:需生成完整树后逐一考察,计算开销大。
四、连续值与缺失值的处理
实际数据中常包含连续属性(如"密度""含糖率")或缺失值,需特殊处理。
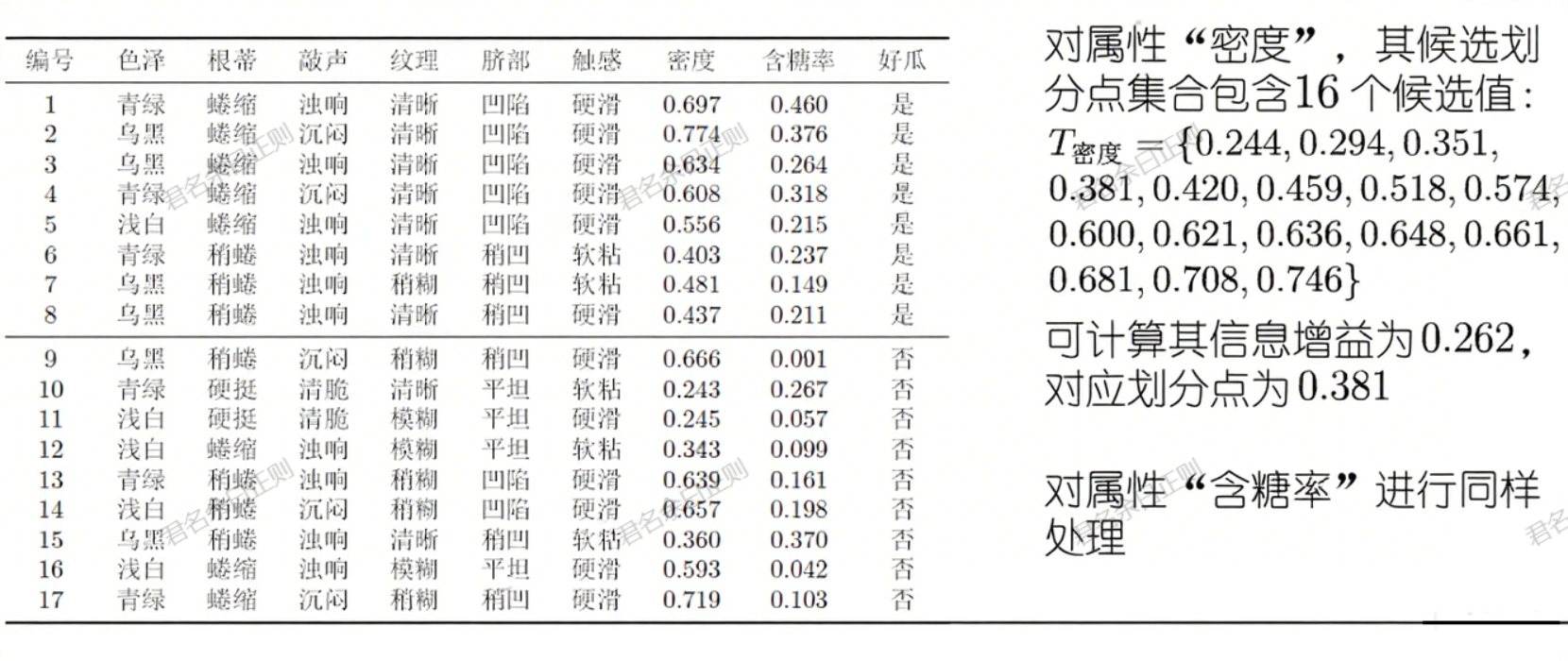
(一)连续值处理(二分法)
- 候选划分点 :将连续属性a的取值从小到大排序为 a 1 , . . . , a n a^1,...,a^n a1,...,an,取相邻值的中位点作为候选划分点:
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } T_a=\left\{\frac{a^i+a^{i+1}}{2} \mid 1\leq i \leq n-1\right\} Ta={2ai+ai+1∣1≤i≤n−1} - 最优划分点:计算每个候选点的信息增益,选择增益最大的点作为划分点,将样本分为"≤t"和">t"两类。
- 示例 :属性"密度"的候选划分点包括0.244、0.294等,通过计算信息增益选择最优划分点。
(二)缺失值处理
需解决两个问题:如何选择划分属性,以及如何划分含缺失值的样本。
-
划分属性选择:
- 定义无缺失值样本子集 D ~ \tilde{D} D~,计算其占总样本的比例 ρ \rho ρ、各类别占比 p ~ k \tilde{p}_k p~k、属性a各取值占比 r ~ v \tilde{r}_v r~v;
- 信息增益修正为: G a i n ( D , a ) = ρ × [ E n t ( D ~ ) − ∑ v = 1 V r ~ v E n t ( D ~ v ) ] Gain(D,a)=\rho \times [Ent(\tilde{D})-\sum_{v=1}^V \tilde{r}_v Ent(\tilde{D}^v)] Gain(D,a)=ρ×[Ent(D~)−∑v=1Vr~vEnt(D~v)],其中 E n t ( D ~ ) = − ∑ k p ~ k log 2 p ~ k Ent(\tilde{D})=-\sum_k \tilde{p}_k \log_2 \tilde{p}_k Ent(D~)=−∑kp~klog2p~k。
-
样本划分:
- 若样本在属性a上取值已知,划入对应子节点,权重不变;
- 若取值缺失,按 r ~ v \tilde{r}_v r~v(属性a取值 a v a^v av的比例)将样本权重分配到各子节点(即 w x × r ~ v w_x \times \tilde{r}_v wx×r~v)。
五、多变量决策树
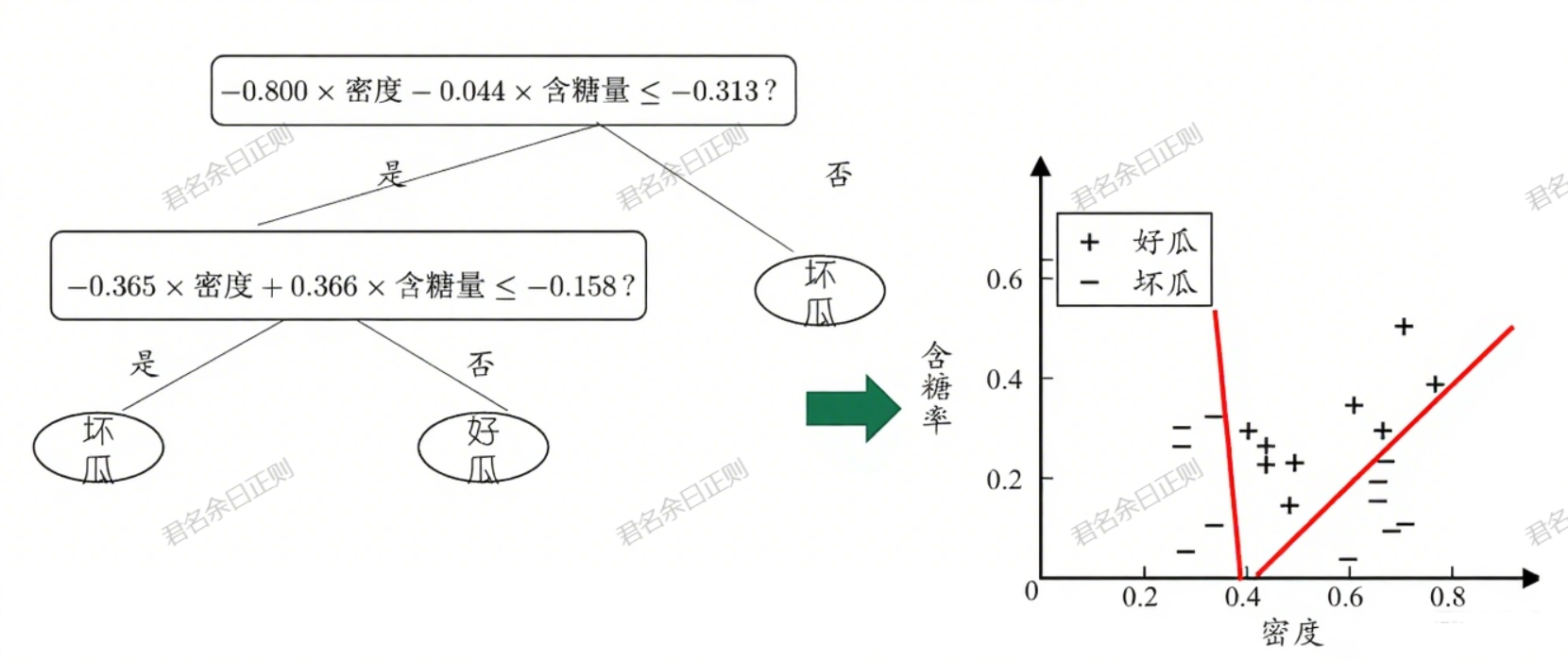
传统决策树(单变量)的非叶节点仅测试单个属性,分类边界与坐标轴平行;多变量决策树的非叶节点是多个属性的线性组合,分类边界更灵活。
(一)核心特点
- 每个非叶节点对应一个线性分类器: ∑ i = 1 d w i a i = t \sum_{i=1}^d w_i a_i = t ∑i=1dwiai=t,其中 w i w_i wi是属性 a i a_i ai的权重,t是阈值,两者通过样本集学习得到。
- 优势:能拟合复杂的分类边界,减少决策树深度,提升泛化能力。
- 示例:通过"-0.800×密度 -0.044×含糖量 < -0.313"这样的线性组合划分样本,比单属性划分更精准。
六、经典决策树算法与工具
- 算法:ID3(信息增益)、C4.5(增益率,支持连续值和缺失值)、C5.0(C4.5的改进版,效率更高)、CART(基尼指数,可用于分类和回归);
- 工具:J48(WEKA中C4.5的实现)等。
上一章: 机器学习03------线性模型
下一章: 机器学习05------多分类学习与类别不平衡
机器学习实战项目: 【从 0 到 1 落地】机器学习实操项目目录:覆盖入门到进阶,大学生就业 / 竞赛必备