上一章: 机器学习05------多分类学习与类别不平衡
下一章: 机器学习07------贝叶斯分类器
机器学习实战项目: 【从 0 到 1 落地】机器学习实操项目目录:覆盖入门到进阶,大学生就业 / 竞赛必备
文章目录
一、间隔与支持向量(SVM的核心思想)
支持向量机(SVM)的核心是在样本空间中寻找最优超平面,实现对不同类别样本的分隔,其关键在于最大化间隔以提升泛化能力。
(一)超平面与间隔
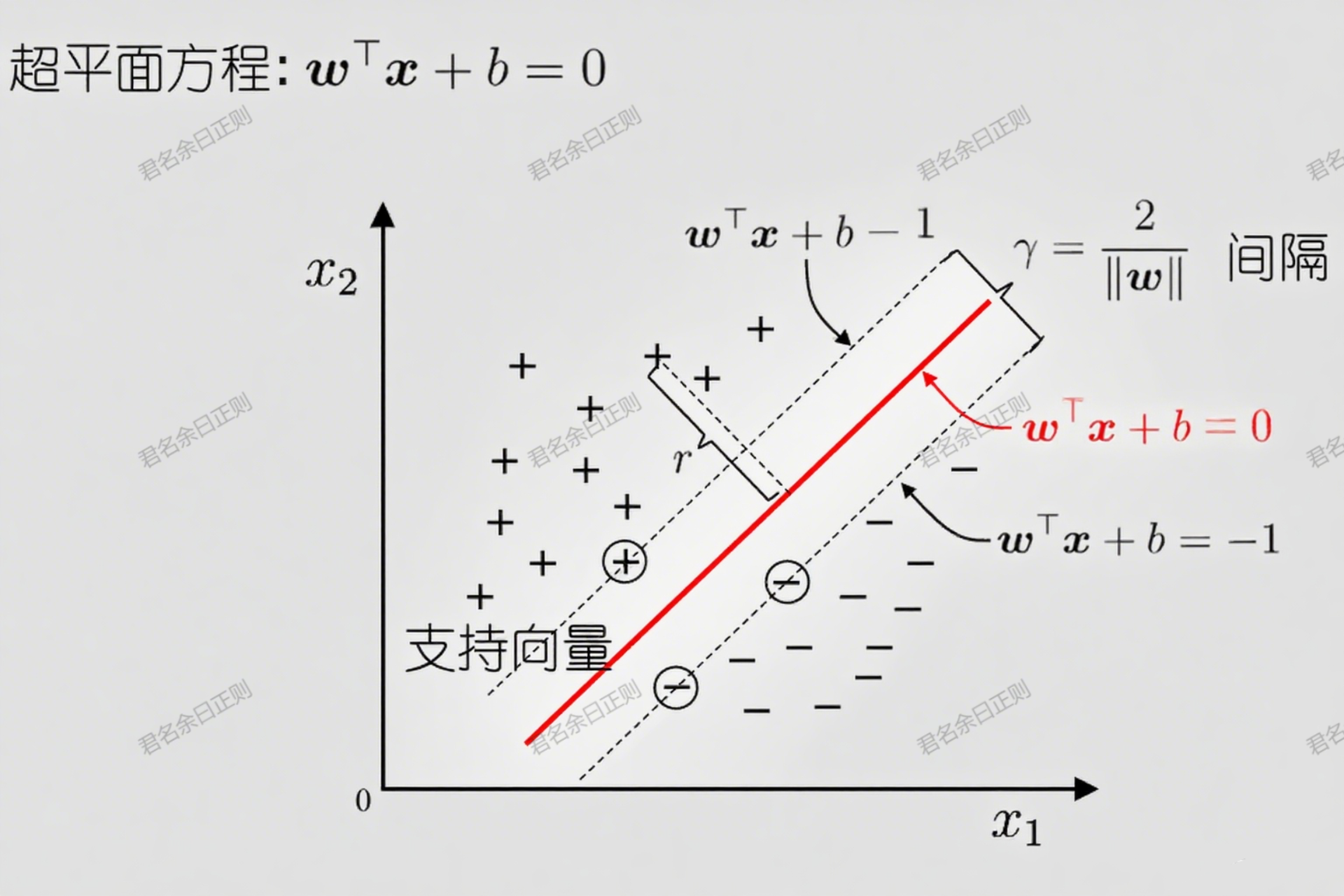
- 超平面方程 :在d维样本空间中,超平面可表示为 w ⊤ x + b = 0 w^\top x + b = 0 w⊤x+b=0,其中 w w w为法向量(决定超平面方向), b b b为偏置项(决定超平面位置)。
- 间隔定义 :样本到超平面的距离称为间隔。对于两类样本,需同时考虑正例和反例到超平面的距离,其中支持向量 (离超平面最近的样本)决定了"最大间隔"------即超平面与两侧支持向量的距离之和( 2 / ∥ w ∥ 2/\|w\| 2/∥w∥)。
- 最优超平面 :目标是找到参数 w w w和 b b b,使间隔最大,即:
a r g m a x w , b 2 ∥ w ∥ s . t . y i ( w ⊤ x i + b ) ≥ 1 , i = 1 , 2 , . . . , m \underset{w, b}{arg max} \frac{2}{\|w\|} \quad s.t. \quad y_i(w^\top x_i + b) \geq 1, \, i=1,2,...,m w,bargmax∥w∥2s.t.yi(w⊤xi+b)≥1,i=1,2,...,m
(约束条件确保所有样本都在间隔外侧, y i y_i yi为样本标签,+1或-1)。
该问题可等价转化为最小化 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^2 21∥w∥2(简化计算)。
二、对偶问题(SVM的求解转化)
为简化最优超平面的求解,SVM通过拉格朗日乘子法将原始问题转化为对偶问题,便于引入核函数并利用解的稀疏性。
(一)对偶问题的推导
- 拉格朗日函数 :引入拉格朗日乘子 α i ≥ 0 \alpha_i \geq 0 αi≥0,构造函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 m α i ( y i ( w ⊤ x i + b ) − 1 ) L(w, b, \alpha) = \frac{1}{2}\|w\|^2 - \sum_{i=1}^m \alpha_i\left(y_i(w^\top x_i + b) - 1\right) L(w,b,α)=21∥w∥2−i=1∑mαi(yi(w⊤xi+b)−1) - 偏导为零条件 :对 w w w和 b b b求偏导并令其为零,得到:
w = ∑ i = 1 m α i y i x i , ∑ i = 1 m α i y i = 0 w = \sum_{i=1}^m \alpha_i y_i x_i, \quad \sum_{i=1}^m \alpha_i y_i = 0 w=i=1∑mαiyixi,i=1∑mαiyi=0 - 对偶问题 :将上述结果回代,原始问题转化为最大化:
∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i ⊤ x j \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j x_i^\top x_j i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxi⊤xj
约束为 ∑ i = 1 m α i y i = 0 \sum_{i=1}^m \alpha_i y_i = 0 ∑i=1mαiyi=0且 α i ≥ 0 \alpha_i \geq 0 αi≥0。
(二)解的稀疏性
根据KKT条件,仅支持向量对应的 α i > 0 \alpha_i > 0 αi>0(非支持向量的 α i = 0 \alpha_i = 0 αi=0),因此最终模型仅依赖支持向量:
f ( x ) = w ⊤ x + b = ∑ i = 1 m α i y i x i ⊤ x + b f(x) = w^\top x + b = \sum_{i=1}^m \alpha_i y_i x_i^\top x + b f(x)=w⊤x+b=i=1∑mαiyixi⊤x+b
这种稀疏性使SVM在预测时仅需计算与支持向量的内积,提升效率。
三、核函数(处理线性不可分问题)
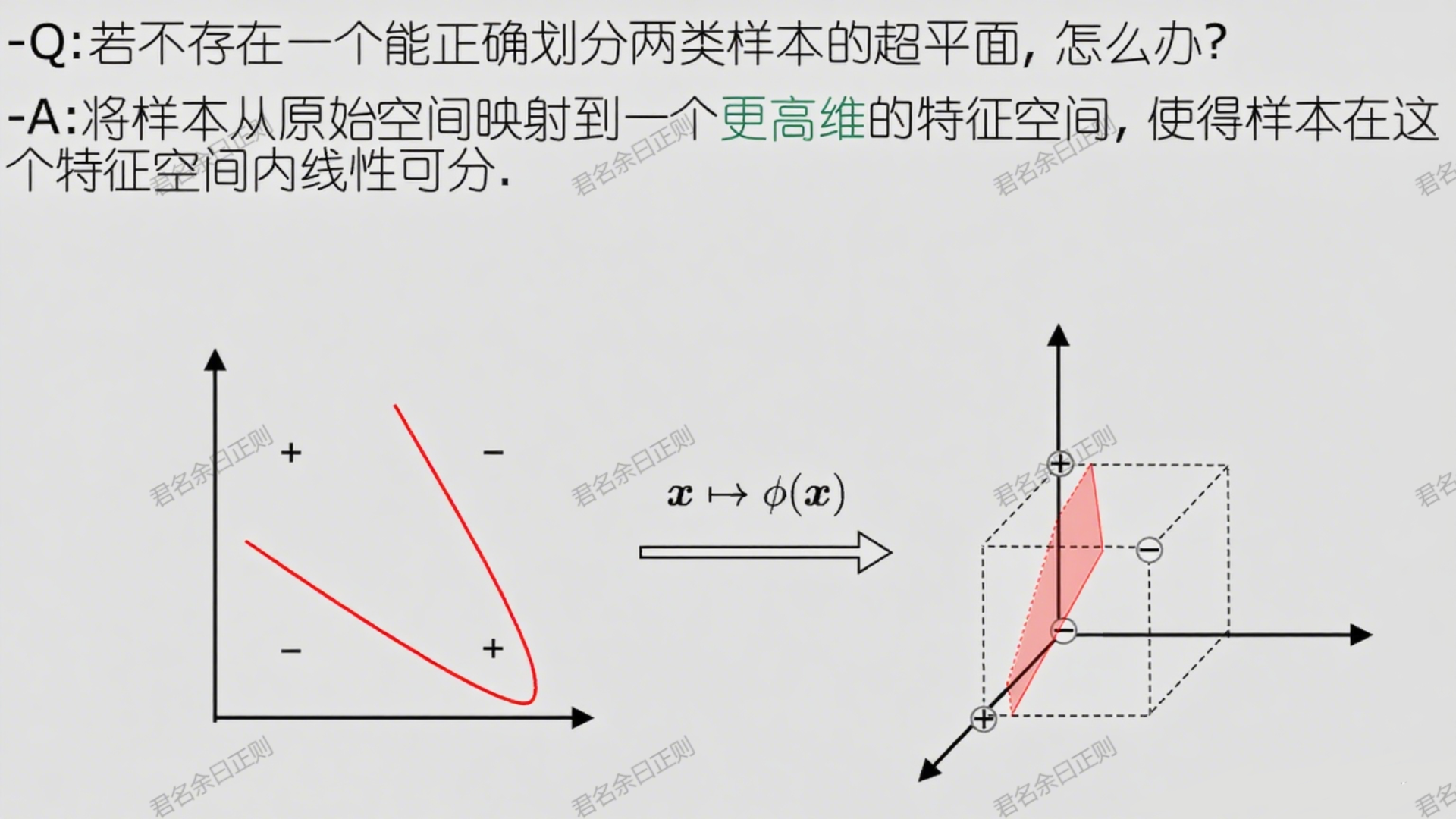
当样本在原始空间线性不可分时,SVM通过核函数将样本映射到高维特征空间,使其线性可分,同时避免显式计算高维映射。
(一)核函数的作用
- 映射与内积 :设样本 x x x在高维空间的映射为 ϕ ( x ) \phi(x) ϕ(x),则超平面可表示为 f ( x ) = w ⊤ ϕ ( x ) + b f(x) = w^\top \phi(x) + b f(x)=w⊤ϕ(x)+b。核函数 κ ( x i , x j ) = ϕ ( x i ) ⊤ ϕ ( x j ) \kappa(x_i, x_j) = \phi(x_i)^\top \phi(x_j) κ(xi,xj)=ϕ(xi)⊤ϕ(xj)直接计算高维空间内积,避免维度灾难。
- Mercer定理:若一个对称函数对应的核矩阵半正定,则它可作为核函数使用(保证映射存在)。
(二)常用核函数
| 名称 | 表达式 | 参数说明 |
|---|---|---|
| 线性核 | κ ( x i , x j ) = x i ⊤ x j \kappa(x_i, x_j) = x_i^\top x_j κ(xi,xj)=xi⊤xj | 适用于线性可分数据 |
| 多项式核 | κ ( x i , x j ) = ( x i ⊤ x j + 1 ) d \kappa(x_i, x_j) = (x_i^\top x_j + 1)^d κ(xi,xj)=(xi⊤xj+1)d | d ≥ 1 d \geq 1 d≥1为多项式次数 |
| 高斯核 | κ ( x i , x j ) = exp ( − ∣ x i − x j ∣ 2 2 δ 2 ) \kappa(x_i, x_j) = \exp(-\frac{|x_i - x_j|^2}{2\delta^2}) κ(xi,xj)=exp(−2δ2∣xi−xj∣2) | δ > 0 \delta > 0 δ>0为带宽(控制平滑度) |
| 拉普拉斯核 | κ ( x i , x j ) = exp ( − ∣ x i − x j ∣ δ ) \kappa(x_i, x_j) = \exp(-\frac{|x_i - x_j|}{\delta}) κ(xi,xj)=exp(−δ∣xi−xj∣) | δ > 0 \delta > 0 δ>0,类似高斯核但更鲁棒 |
| Sigmoid核 | κ ( x i , x j ) = tanh ( β x i ⊤ x j + θ ) \kappa(x_i, x_j) = \tanh(\beta x_i^\top x_j + \theta) κ(xi,xj)=tanh(βxi⊤xj+θ) | β > 0 , θ < 0 \beta > 0, \theta < 0 β>0,θ<0,模拟神经网络 |
四、软间隔与正则化(应对现实数据)
现实中数据常存在噪声或非线性,难以完全线性可分,因此引入"软间隔",允许部分样本不满足间隔约束,通过正则化平衡间隔最大化与错误样本数量。
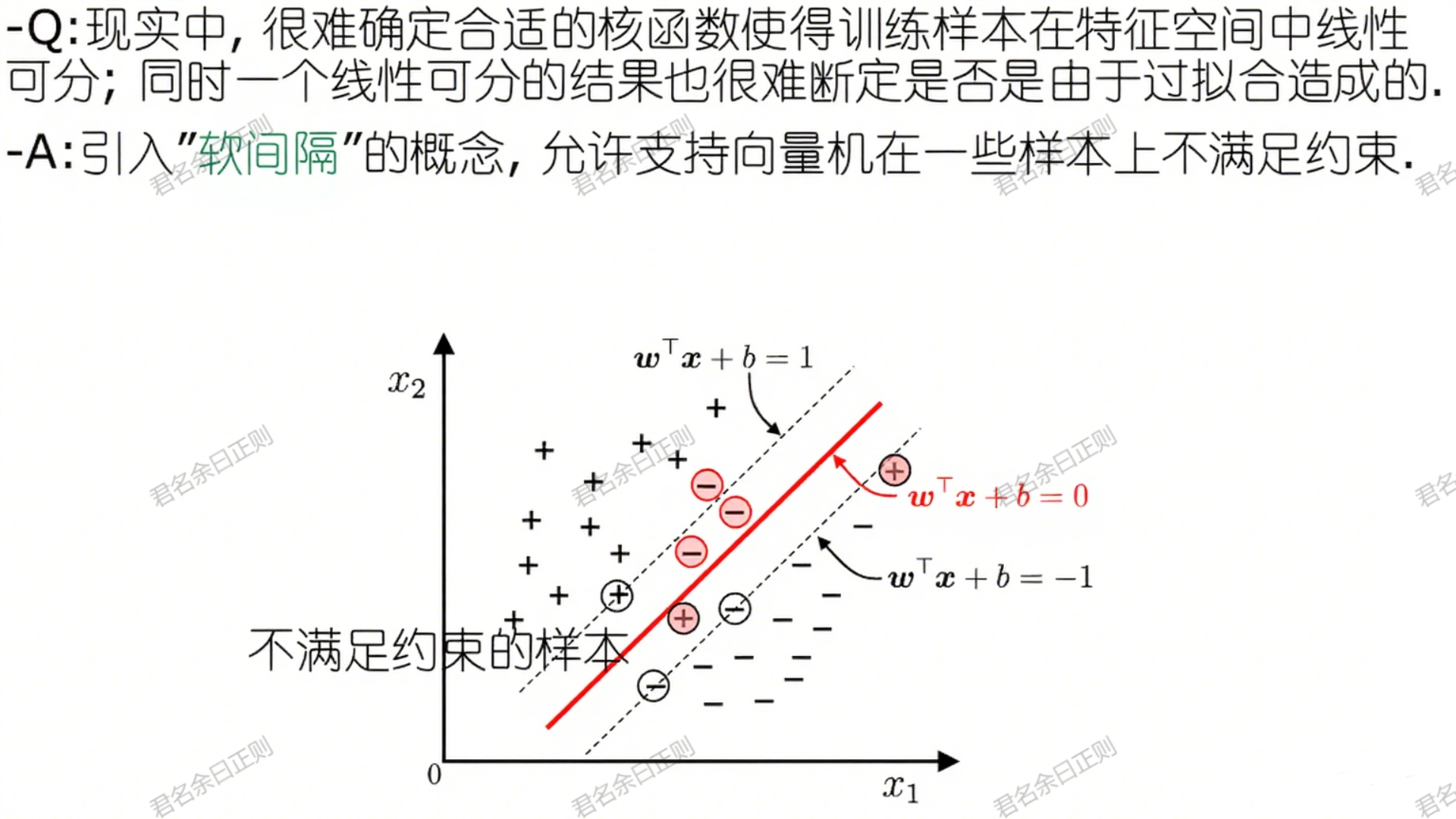
(一)软间隔的原始问题
目标是最小化
1 2 ∥ w ∥ 2 + C ∑ i = 1 m l 0 / 1 ( y i ( w ⊤ ϕ ( x i ) + b ) − 1 ) \frac{1}{2}\|w\|^2 + C\sum_{i=1}^m l_{0/1}(y_i(w^\top \phi(x_i) + b) - 1) 21∥w∥2+Ci=1∑ml0/1(yi(w⊤ϕ(xi)+b)−1)
其中:
- l 0 / 1 l_{0/1} l0/1为0/1损失函数(样本不满足约束时为1,否则为0);
- C > 0 C > 0 C>0为正则化参数,控制对错误样本的惩罚力度( C C C越大,对错误的容忍度越低)。
由于0/1损失函数非凸,实际使用hinge损失 ( l ( z ) = max ( 0 , 1 − z ) l(z) = \max(0, 1 - z) l(z)=max(0,1−z))替代,其数学性质更优且是0/1损失的上界。

(二)对偶问题与正则化
软间隔的对偶问题与硬间隔类似,但 α i \alpha_i αi需满足 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C。正则化项 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^2 21∥w∥2控制模型复杂度,经验风险项 ∑ l ( ⋅ ) \sum l(\cdot) ∑l(⋅)控制训练误差,形成结构风险最小化框架,可推广至其他模型(如LASSO、逻辑回归)。
五、支持向量回归(SVR)
SVM不仅用于分类,还可扩展为回归模型(SVR),允许预测值与真实值存在一定偏差( ϵ \epsilon ϵ间隔带),以保持稀疏性。
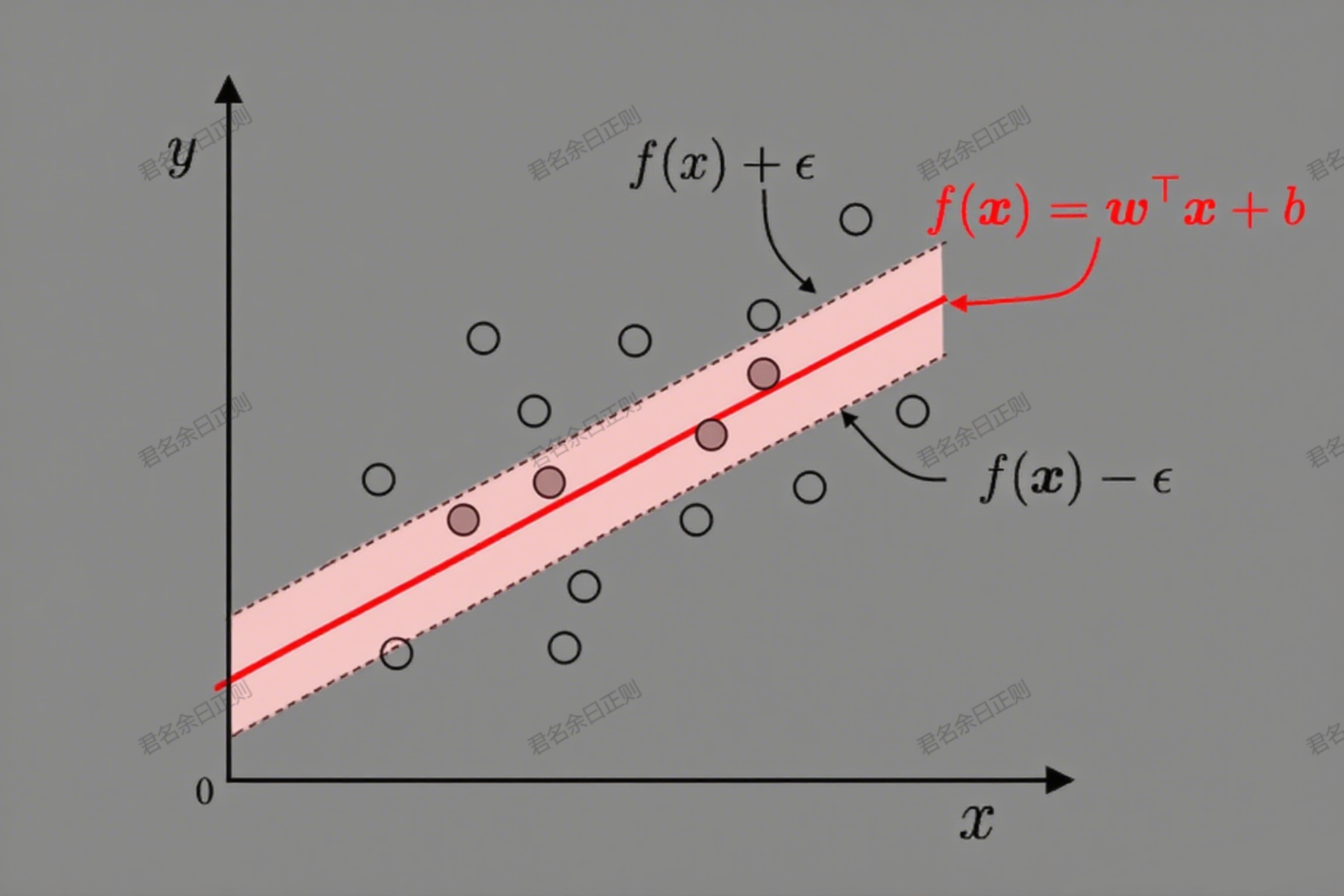
(一)核心思想
- 间隔带 :当预测值 f ( x i ) f(x_i) f(xi)与真实值 y i y_i yi的偏差在 ϵ \epsilon ϵ以内时,损失为0;超出则计算损失( ξ i + ξ ^ i \xi_i + \hat{\xi}_i ξi+ξ^i,分别对应高估和低估)。
- 原始问题 :
min w , b , ξ i , ξ ^ i 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ( ξ i + ξ ^ i ) \min_{w, b, \xi_i, \hat{\xi}i} \frac{1}{2}\|w\|^2 + C\sum{i=1}^m (\xi_i + \hat{\xi}_i) w,b,ξi,ξ^imin21∥w∥2+Ci=1∑m(ξi+ξ^i)
约束为 y i − f ( x i ) ≤ ϵ + ξ i y_i - f(x_i) \leq \epsilon + \xi_i yi−f(xi)≤ϵ+ξi, f ( x i ) − y i ≤ ϵ + ξ ^ i f(x_i) - y_i \leq \epsilon + \hat{\xi}_i f(xi)−yi≤ϵ+ξ^i, ξ i , ξ ^ i ≥ 0 \xi_i, \hat{\xi}_i \geq 0 ξi,ξ^i≥0。
(二)对偶与预测
SVR的对偶问题通过引入 α i \alpha_i αi和 α ^ i \hat{\alpha}i α^i求解,最终模型为:
f ( x ) = ∑ i = 1 m ( α ^ i − α i ) κ ( x i , x ) + b f(x) = \sum{i=1}^m (\hat{\alpha}_i - \alpha_i) \kappa(x_i, x) + b f(x)=i=1∑m(α^i−αi)κ(xi,x)+b
仅与支持向量(偏差超出 ϵ \epsilon ϵ的样本)有关,保持稀疏性。
六、核方法(扩展与推广)
核函数的思想可推广至其他线性模型,形成"核化"模型,通过高维映射提升非线性拟合能力。
(一)表示定理
任何基于核函数的学习模型,其最优解均可表示为训练样本核函数的线性组合,即 h ∗ ( x ) = ∑ i = 1 m α i κ ( x i , x ) + b h^*(x) = \sum_{i=1}^m \alpha_i \kappa(x_i, x) + b h∗(x)=∑i=1mαiκ(xi,x)+b。这为核方法的通用性提供了理论基础。
(二)常见核化模型
- 核LDA:将样本映射到高维空间后做线性判别分析,提升分类效果;
- 核PCA:在高维空间进行主成分分析,更好地提取非线性特征。
七、实用工具与软件包
成熟的SVM工具包包括LIBSVM、SVMlight等,支持分类、回归及多种核函数,广泛应用于实际任务(如文档分类、图像识别)。
上一章: 机器学习05------多分类学习与类别不平衡
下一章: 机器学习07------贝叶斯分类器
机器学习实战项目: 【从 0 到 1 落地】机器学习实操项目目录:覆盖入门到进阶,大学生就业 / 竞赛必备