目录
[5）环形队列的实现 leecode622](#5）环形队列的实现 leecode622)
视频链接
【算法讲解013【入门】队列和栈-链表、数组实现】
1）队列的介绍
先进先出。进了从尾进，从头出。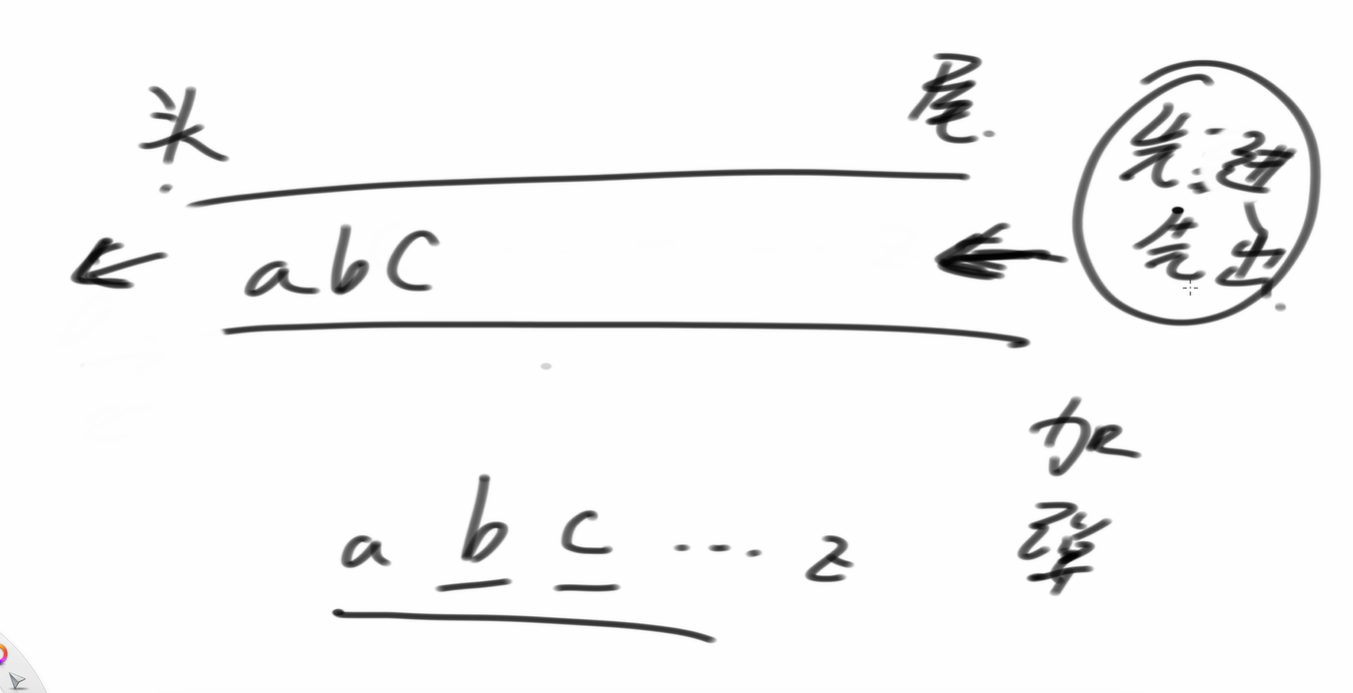
队列我们认为范围是左闭右开的。范围是[L，R），因此如果L<R,就说明有元素，如果L==R，说明队列里没有元素。
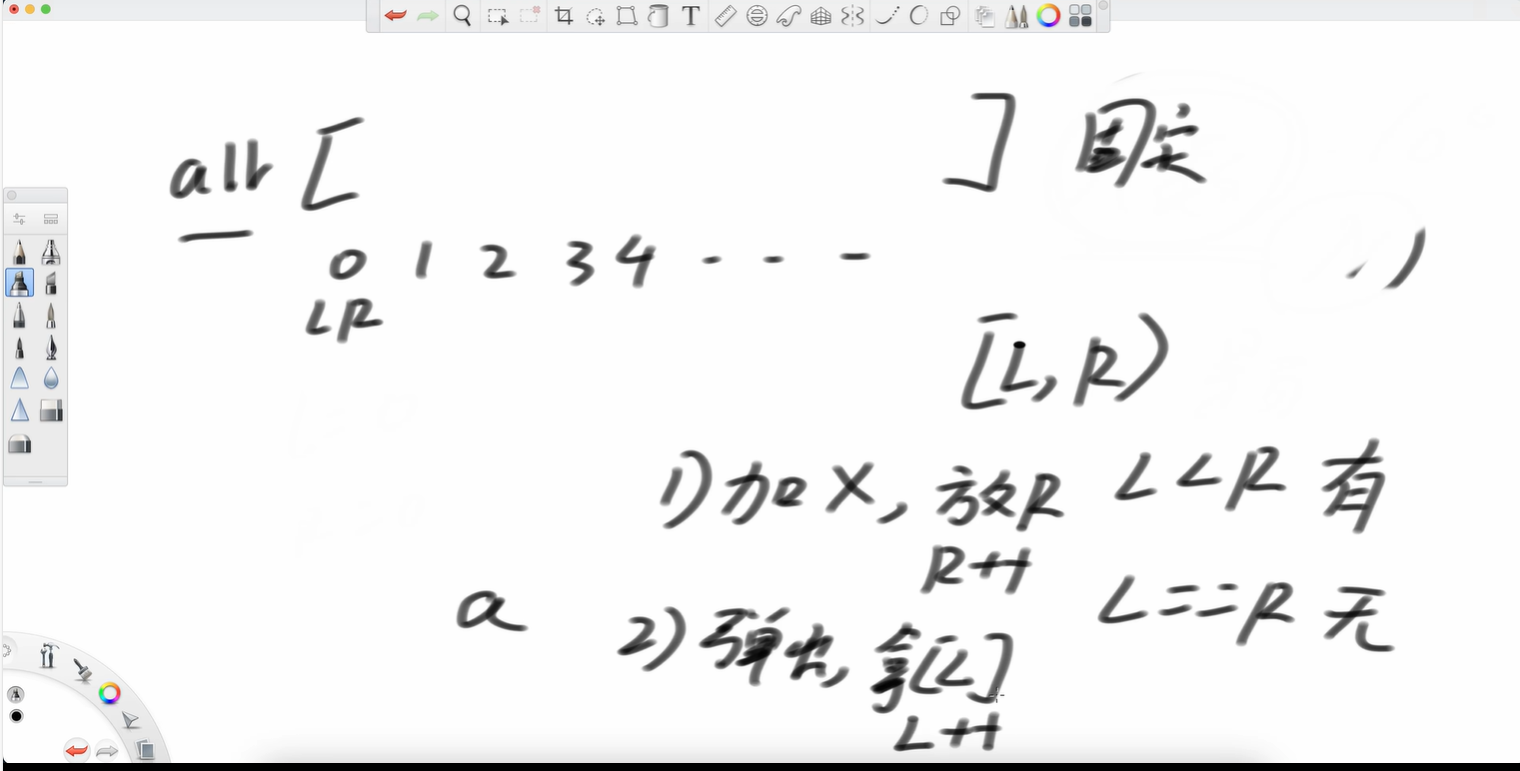
如果我们想加b到R位置，那么我们R++；（原来R在1位置）
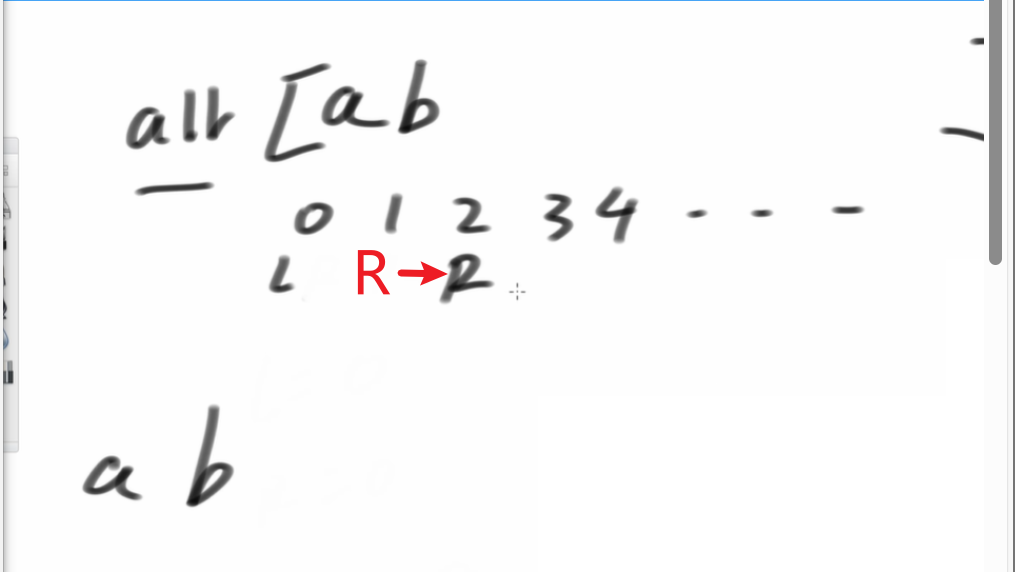
如果我们想让数弹出，那么我们拿L位置的数，让L++
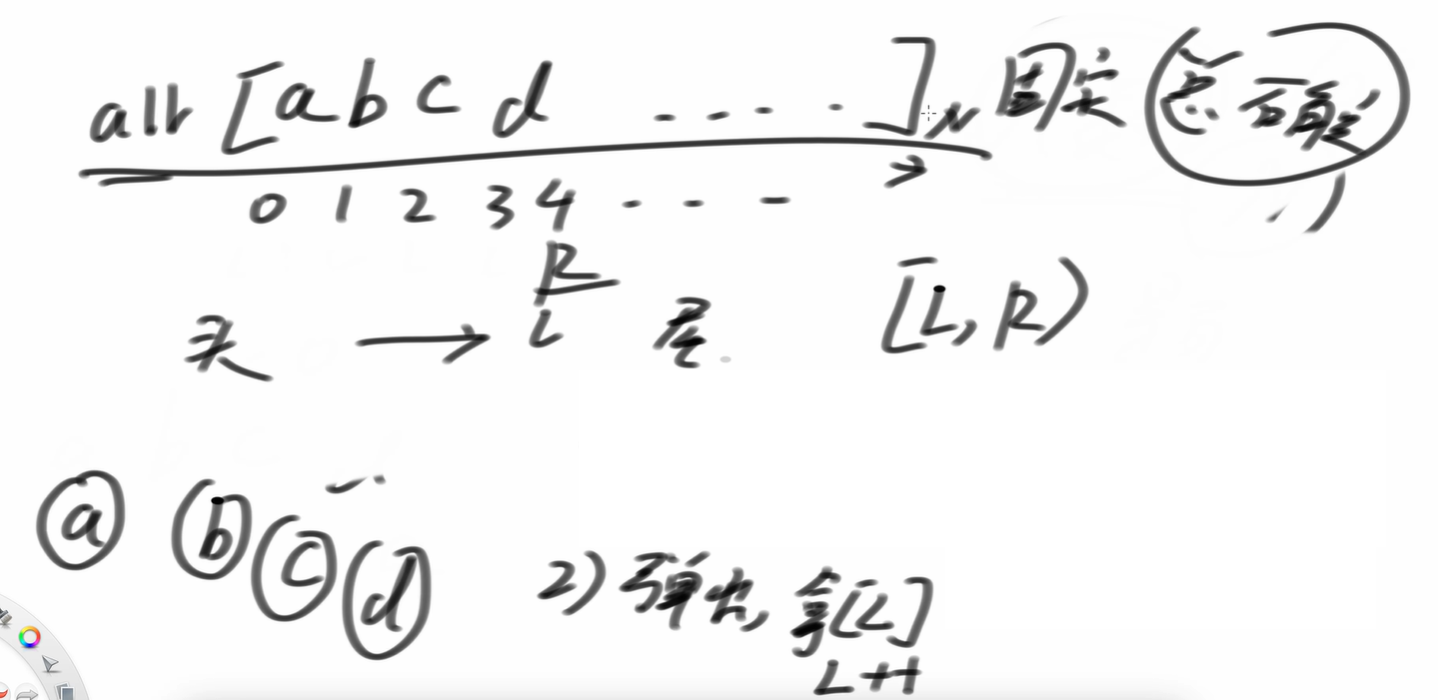
队列是一种遵循 先进先出 (First-In, First-Out, FIFO) 原则的线性数据结构。
可以把它想象成现实生活中的排队：最早来排队的人，最先获得服务并离开。在数据结构中，最早被放入（入队）的元素，也最先被取出（出队）。
核心操作
一个基本的队列通常支持以下几种操作：
-
offer(value) (或 enqueue): 将一个元素添加到队尾。
-
poll() (或 dequeue): 从队头取出一个元素，并将其从队列中移除。
-
peek() (或 head): 查看队头的元素，但不移除它。
-
isEmpty(): 判断队列是否为空。
-
size()：返回队列中元素的个数。
3）队列的链表实现和数组实现
在很多语言中，都有现成的、基于链表实现的队列结构。例如在 Java 中，LinkedList 类就实现了 Queue 接口。
java
// 直接用Java内部的实现
// 其实内部就是双向链表，常数操作
public static class Queue1 {
// java中的双向链表LinkedList就足够了
public Queue<Integer> queue = new LinkedList<>();
// 调用任何方法之前，先调用这个方法来判断队内是否有东西
public boolean isEmpty() {
return queue.isEmpty();
}
// 向队内加入num, 加到队尾
public void offer(int num) {
queue.offer(num);
}
// 从队头拿，从头拿
public int poll() {
return queue.poll();
}
}使用现成的 LinkedList 来实现队列非常简单，因为其双向链表的结构天然支持在头部和尾部进行 O(1) 复杂度的增删操作，完美契合队列的需求。
使用数组实现队列
在笔试和面试中，更常见的要求是让我们手动用数组来实现一个队列。这更能考察我们对数据结构底层实现的理解。
这是一个基础版的数组队列实现：
java
// 实际刷题时更常见的写法，常数时间好
// 如果可以确定加入操作的总次数不超过n，那么可以用
// 一般笔试、面试都会有一个明确数据量，所以这是最常用的方式
public static class Queue2 {
public int[] queue;
public int l; // 头指针
public int r; // 尾指针
// 加入操作的总次数上限是多少，一定要明确
public Queue2(int n) {
queue = new int[n];
l = 0;
r = 0;
}
// 调用任何方法之前，先调用这个方法来判断队内是否有东西
public boolean isEmpty() {
return l == r;
}
// 入队操作
public void offer(int num) {
queue[r++] = num;
}
// 出队操作
public int poll() {
return queue[l++];
}
// 查看队头
public int head() {
return queue[l];
}
// 查看队尾
public int tail() {
return queue[r - 1];
}
// 查看大小
public int size() {
return r - l;
}
}代码解析：
-
结构：我们用一个固定大小的数组 queue 作为容器，并设置两个指针：
-
l (left): 指向队头。下一个要被 poll 的元素就是 queue[l]。
-
r (right): 指向下一个可以插入元素的位置。下一个 offer 的元素将被放入 queue[r]。
-
-
isEmpty(): 当 l 和 r 指针相遇时 (l == r)，说明队列中没有任何元素，队列为空。
-
offer(num): 将元素 num 放入 r 指向的位置，然后将 r 指针后移 (r++)。
-
poll(): 返回 l 指向的元素，然后将 l 指针后移 (l++)。
这种实现的局限性 ：
这个基础版的数组队列有一个明显的问题：指针 l 和 r 只能单向地向右移动。这意味着，即使我们 poll 了很多元素，数组前面空出来的空间也无法被重新利用。当 r 到达数组末尾时，即使队列实际大小很小，我们也无法再 offer 新的元素了。
2）栈的介绍
像弹匣一样，装的时候放在上一个的上面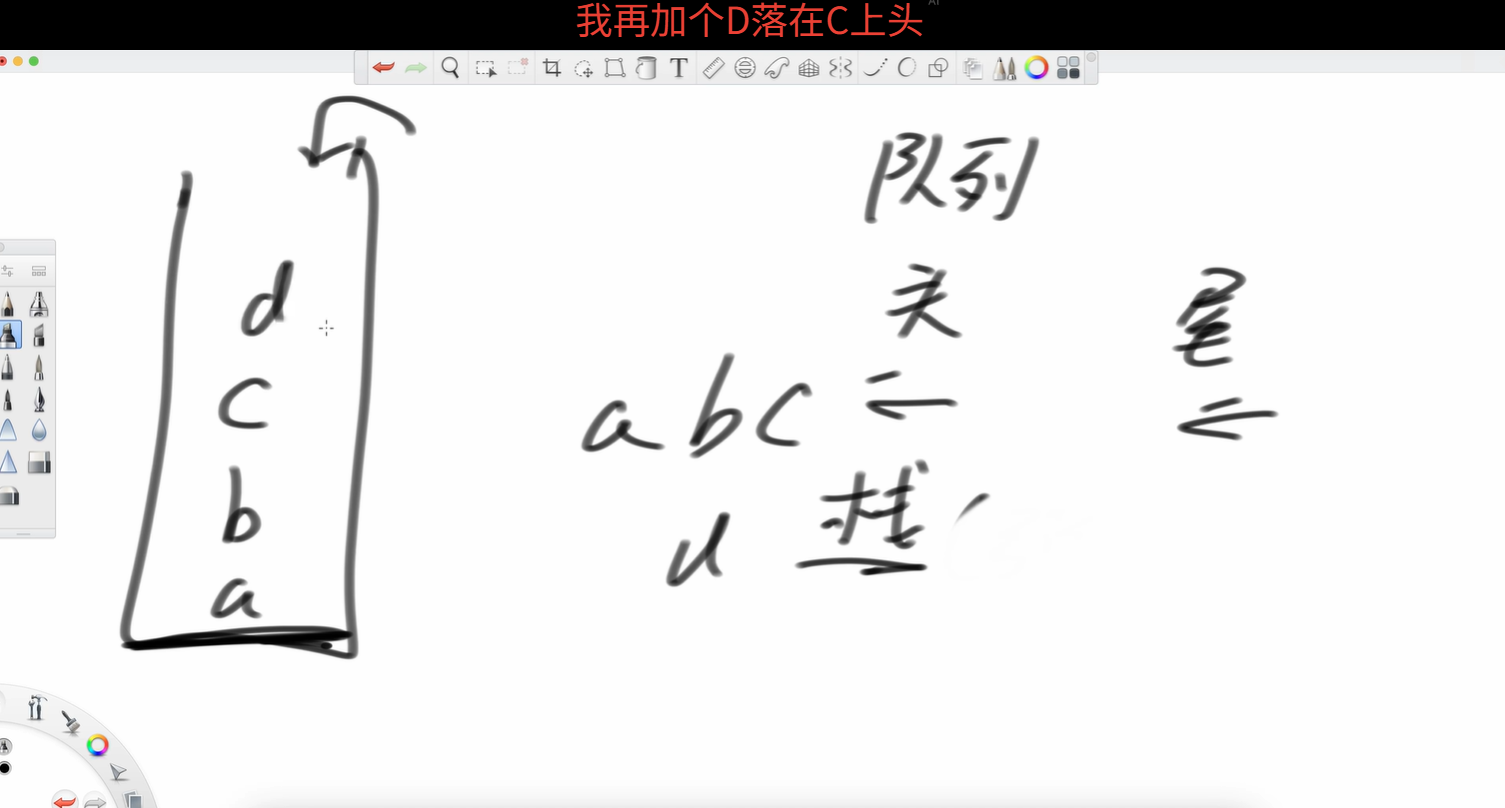
弹出的时候也是上面的先弹出。先d再c等等。
和上面的队类似。
与队列的"先进先出"相反，栈是一种遵循 后进先出 (Last-In, First-Out, LIFO) 原则的线性数据结构。
它最经典的类比就是一摞盘子：我们总是把新盘子放在最上面，而取盘子时，也总是从最上面拿。最后放上去的盘子，最先被取走。
核心操作
一个基本的栈通常支持以下几种操作：
-
push(value): 将一个元素压入栈顶。
-
pop(): 从栈顶弹出一个元素，并将其从栈中移除。
-
peek(): 查看栈顶的元素，但不移除它。
-
isEmpty(): 判断栈是否为空。
-
size()：返回栈中元素的个数。
4）栈的数组实现
使用语言内置的实现
Java 提供了 java.util.Stack 类，可以直接使用。它的底层是动态数组 (Vector)。
java
// 直接用Java内部的实现
// 其实就是动态数组，不过常数时间并不好
public static class Stack1 {
public Stack<Integer> stack = new Stack<>();
// 调用任何方法之前，先调用这个方法来判断栈内是否有东西
public boolean isEmpty() {
return stack.isEmpty();
}
public void push(int num) {
stack.push(num);
}
public int pop() {
return stack.pop();
}
public int peek() {
return stack.peek();
}
public int size() {
return stack.size();
}
}使用数组手动实现栈
这是在笔试、面试中考察的重点。我们通过一个数组和一个指针（或索引）来模拟栈的行为。
java
// 实际刷题时更常见的写法，常数时间好
// 如果可以保证同时在栈里的元素个数不超过n，那么可以用
// 也就是发生弹出操作之后，空间可以复用
// 一般笔试、面试都会有一个明确数据量，所以这是最常用的方式
public static class Stack2 {
public int[] stack;
public int size; // 指针，指向下一个可插入的位置
// 同时在栈里的元素个数不超过n
public Stack2(int n) {
stack = new int[n];
size = 0;
}
// 调用任何方法之前，先调用这个方法来判断栈内是否有东西
public boolean isEmpty() {
return size == 0;
}
// 入栈
public void push(int num) {
stack[size++] = num;
}
// 出栈
public int pop() {
return stack[--size];
}
// 查看栈顶元素
public int peek() {
return stack[size - 1];
}
// 返回栈中元素数量
public int size() {
return size;
}
}代码解析：
-
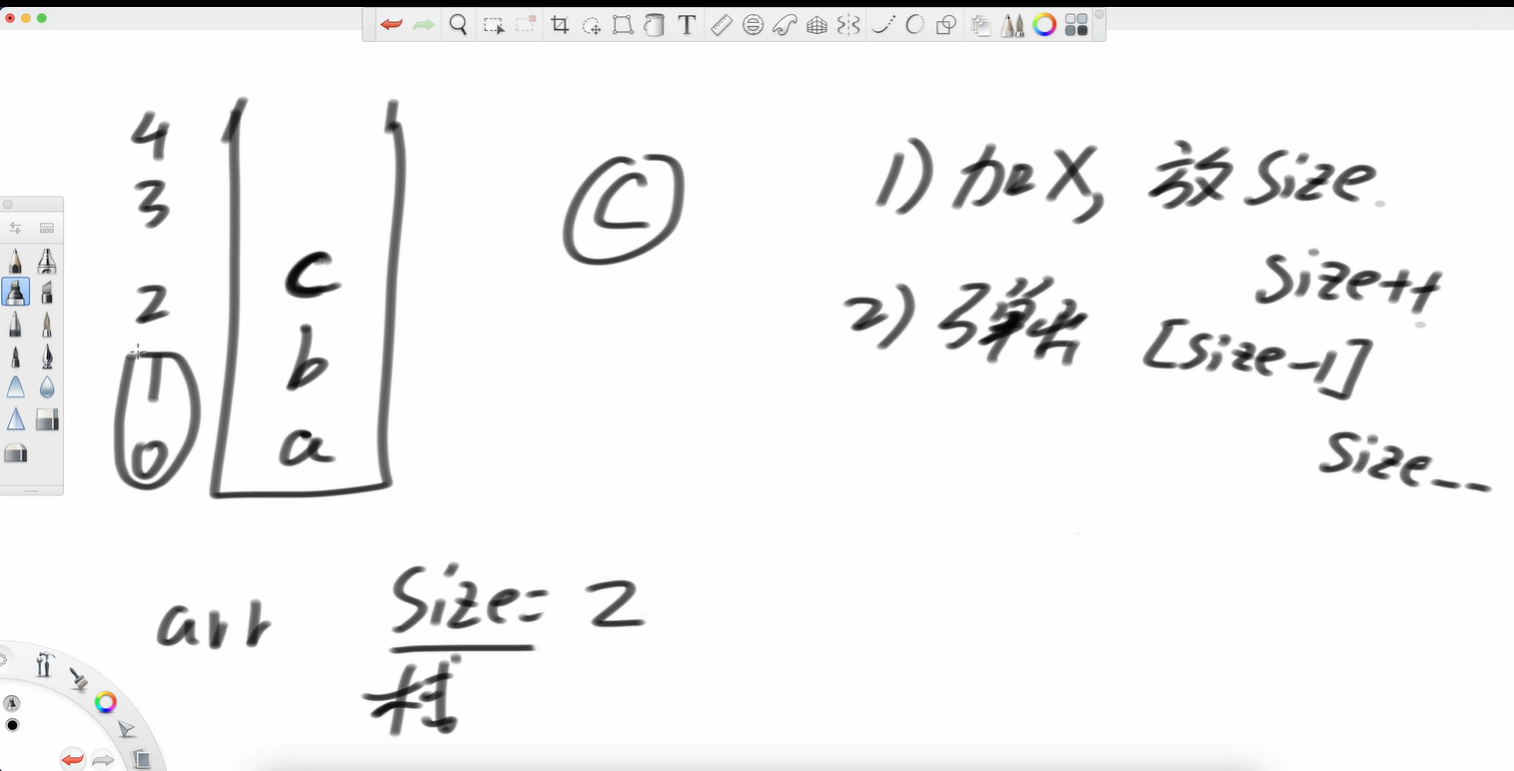
结构 ：我们使用一个固定大小的数组 stack 和一个整型变量 size。这里的 size 非常巧妙，它既表示了栈中当前的元素数量 ，也同时扮演了栈顶指针的角色，指向下一个新元素应该被插入的位置。
-
isEmpty(): 当 size 为 0 时，栈为空。
-
push(num): 将新元素 num 放入 stack[size] 的位置，然后将 size 加一 (size++)。
-
pop(): 先将 size 减一 (--size)，使其指向当前的栈顶元素，然后返回 stack[size]。注意，数据并没有从数组中被"清除"，但它已经变得不可访问，后续的 push 操作会覆盖它。这就是"空间复用"的体现。
-
peek(): 直接返回 stack[size - 1] 的值，因为 size - 1 正是当前栈顶元素的索引。
这种数组实现方式，所有操作的平均时间复杂度都是 O(1)，性能非常好。
5）环形队列的实现 leecode622
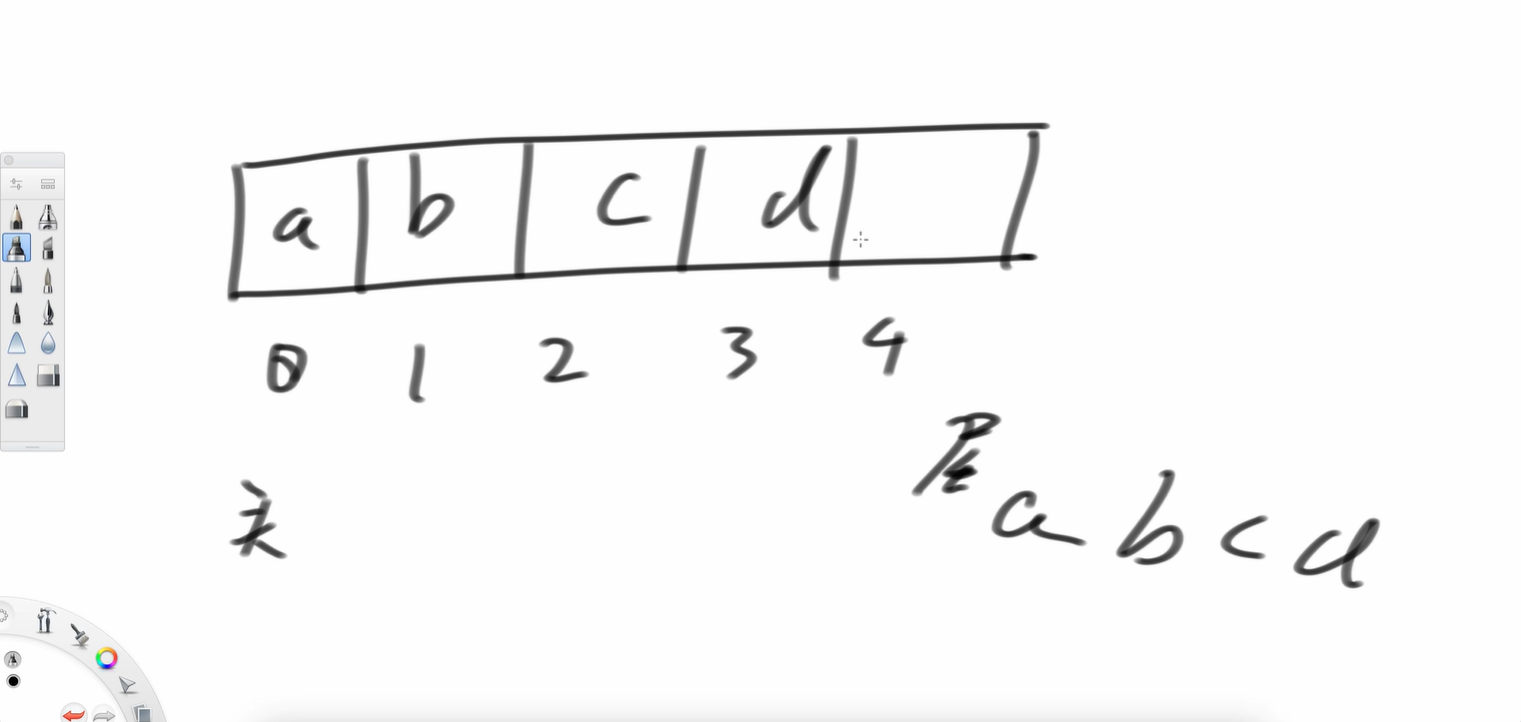
举个例子，一共有五个位置，abcd依次放进去，a位置是头，d位置是尾，此时我想把a弹出，就像上文中的队列弹出，空间释放。头往后去。我再弹出个b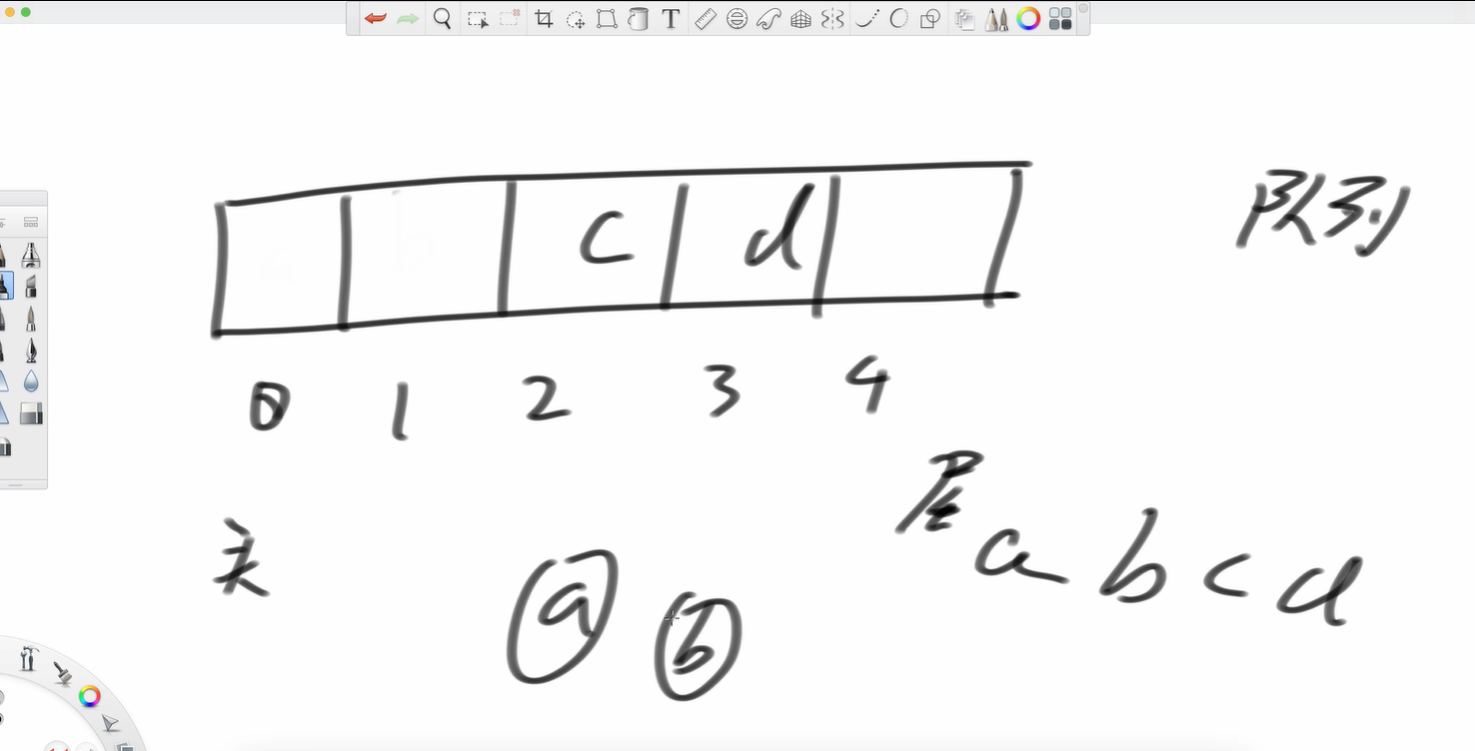
接着我再加个e呢？
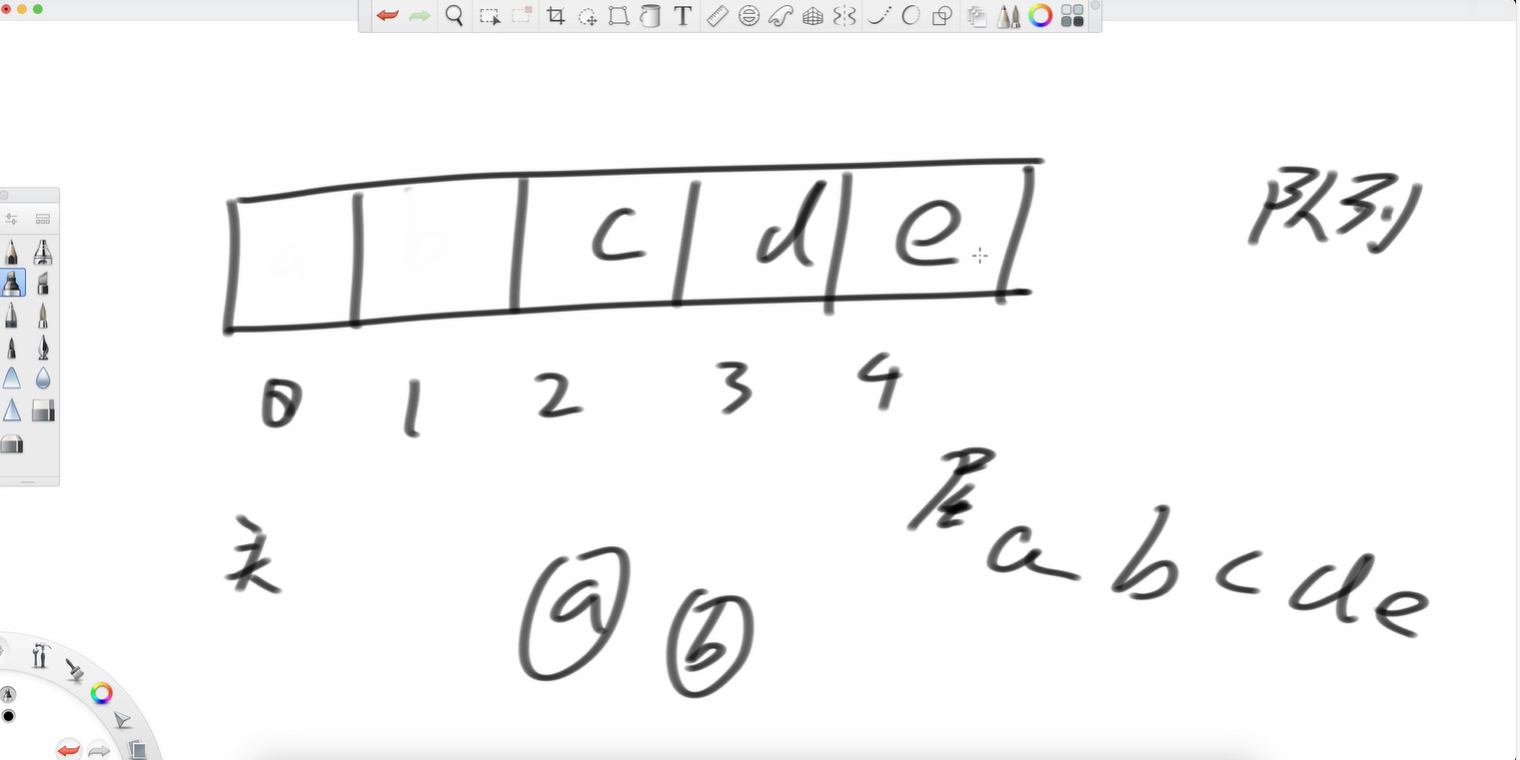
我要是再加个f呢？
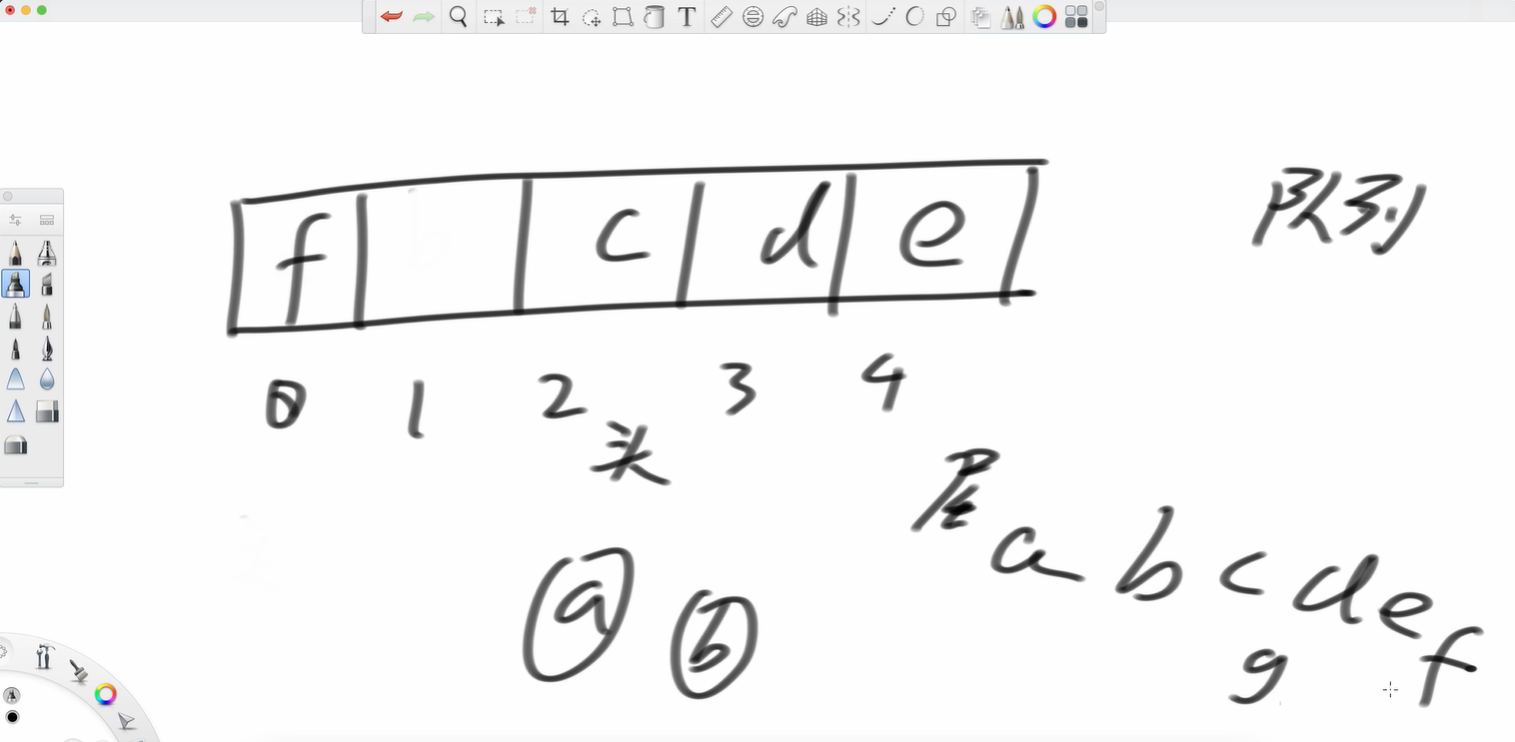
但注意，c位置是头。
再加个g呢？
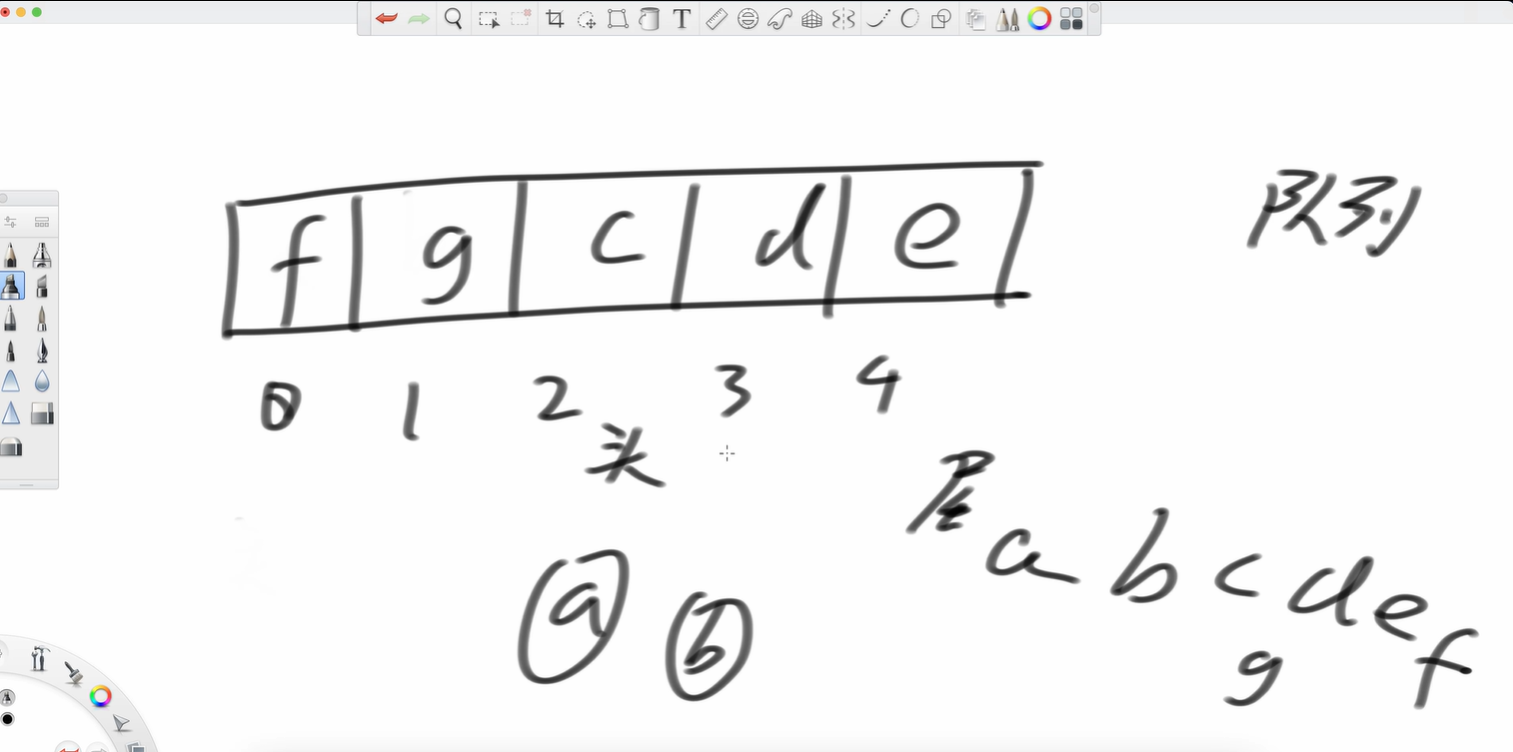
所以这就是个环形结构
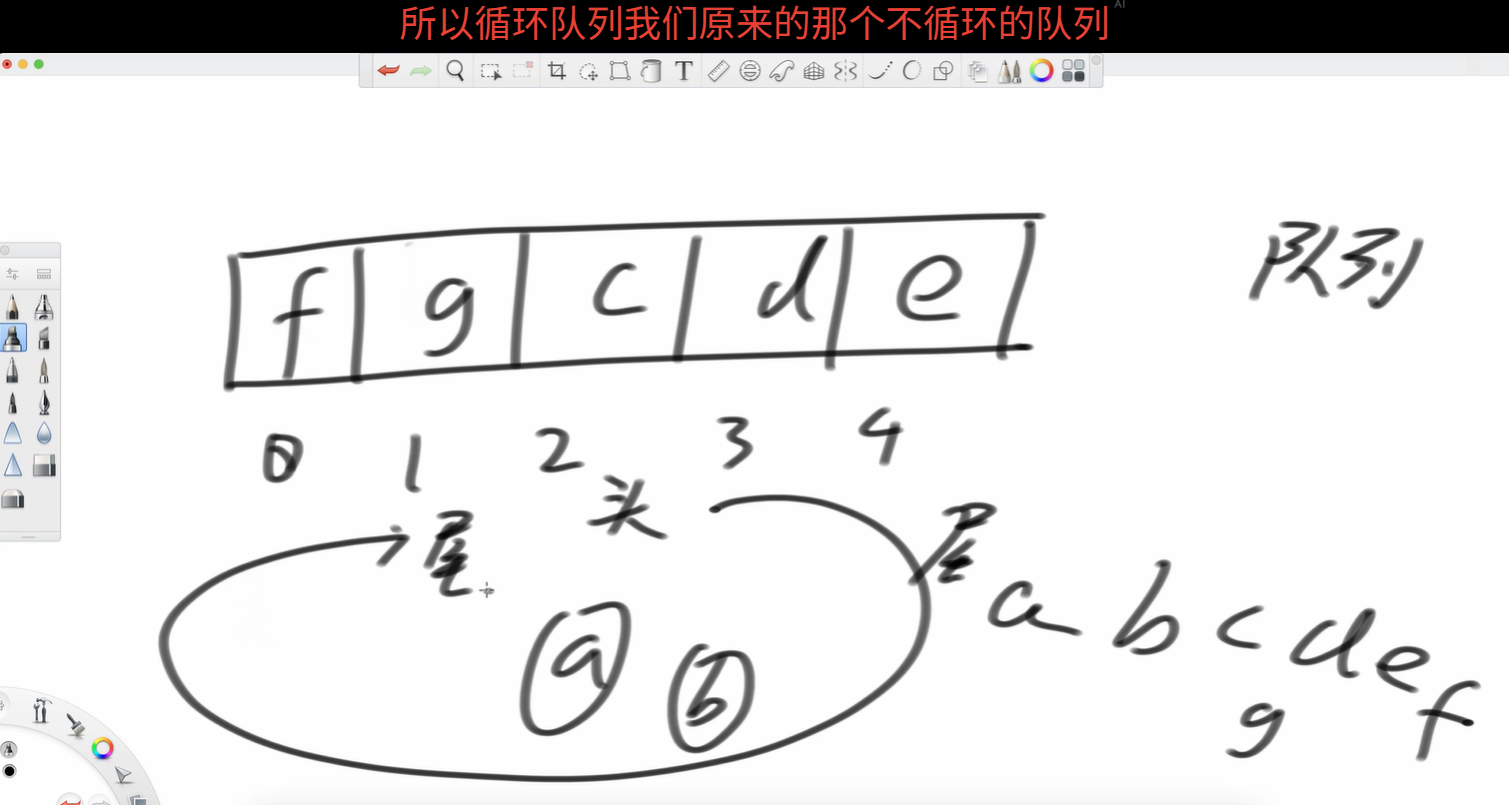所以只要你不同时多于5个在这个队列里，就能一直保持着环形队列继续下去。
那怎么写代码呢？
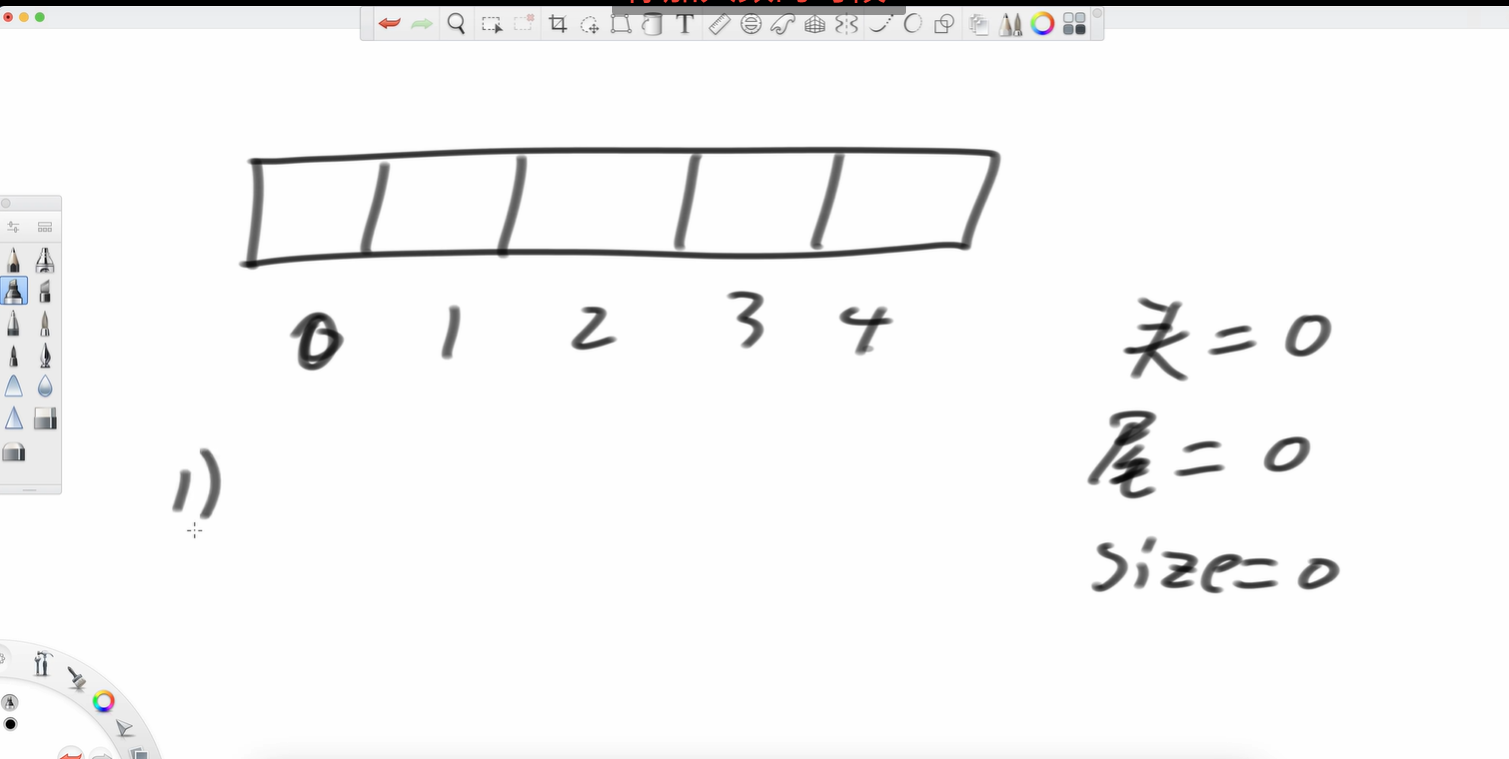
前提：size允许才能做操作一和操作二
这道题limit就是5
我现在要加入a
我再加个b，再加个c
弹出a
再加个d呢
再弹出b
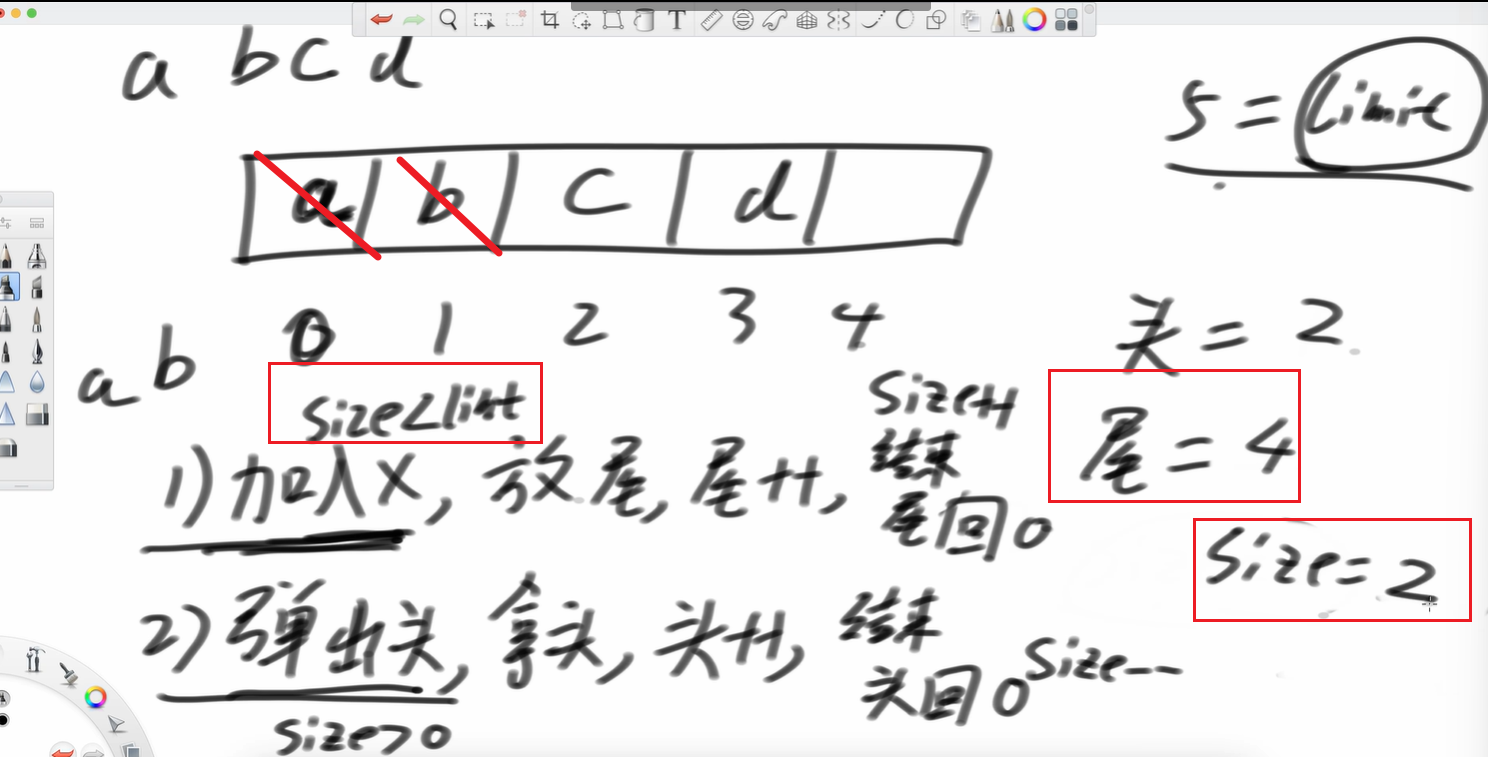
再加个e
再加个f 放到尾巴的位置，这不就复用了吗？
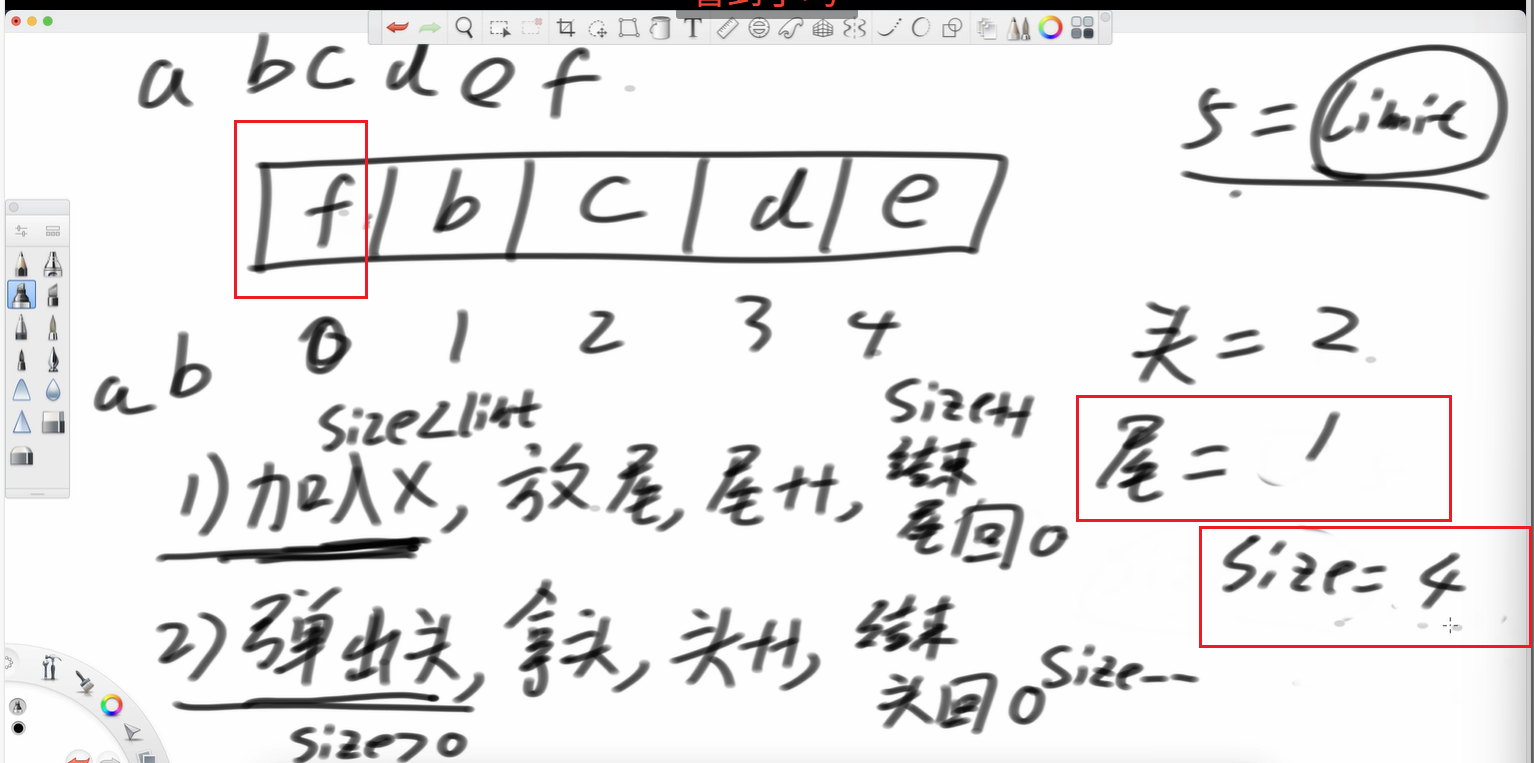https://leetcode.cn/problems/design-circular-queue/
java
// 设计循环队列
// 测试链接 : https://leetcode.cn/problems/design-circular-queue/
class MyCircularQueue {
public int[] queue;
public int l; // 头指针
public int r; // 尾指针
public int size; // 当前队列大小
public int limit; // 队列容量
// 构造器，设置队列长度为 k
public MyCircularQueue(int k) {
queue = new int[k];
l = r = size = 0;
limit = k;
}
// 向循环队列插入一个元素。如果成功插入则返回真
public boolean enQueue(int value) {
if (isFull()) {
return false;
} else {
queue[r] = value;
// r++, 结束了，跳回0
r = r == limit - 1 ? 0 : (r + 1);
size++;
return true;
}
}
// 从循环队列中删除一个元素。如果成功删除则返回真
public boolean deQueue() {
if (isEmpty()) {
return false;
} else {
// l++, 结束了，跳回0
l = l == limit - 1 ? 0 : (l + 1);
size--;
return true;
}
}
// 从队首获取元素。如果队列为空，返回 -1
public int Front() {
if (isEmpty()) {
return -1;
} else {
return queue[l];
}
}
// 获取队尾元素。如果队列为空，返回 -1
public int Rear() {
if (isEmpty()) {
return -1;
} else {
// r 指向的是下一个要插入的位置，所以队尾元素在 r 的前一个位置
// 需要计算 r 的前一个位置，同样要考虑循环
int last = r == 0 ? (limit - 1) : (r - 1);
return queue[last];
}
}
// 检查循环队列是否为空
public boolean isEmpty() {
return size == 0;
}
// 检查循环队列是否已满
public boolean isFull() {
return size == limit;
}
}代码解析
-
成员变量：
-
l 和 r：与之前一样，分别是头指针和尾指针。
-
limit：数组的总容量，即队列的容量上限。
-
size：核心变量。我们引入一个 size 变量来实时记录队列中元素的个数。这使得判断队列是"空"还是"满"变得极其简单，避免了复杂的指针位置判断。
-
-
enQueue(value) 入队：
-
首先通过 isFull() 判断队列是否已满。
-
queue[r] = value;：在尾指针 r 的位置放入新元素。
-
r = r == limit - 1 ? 0 : (r + 1);：环形逻辑的关键 。更新尾指针 r。如果 r 已经到达数组的最后一个位置 (limit - 1)，则下一步就让它跳回到 0；否则，就正常 +1。
-
size++：队列大小加一。
-
-
deQueue() 出队：
-
首先通过 isEmpty() 判断队列是否为空。
-
l = l == limit - 1 ? 0 : (l + 1);：环形逻辑的关键。更新头指针 l。与 r 的逻辑完全相同，如果 l 到达末尾，就跳回 0。
-
size--：队列大小减一。
-
-
Front() 查看队头：
- 如果队列不为空，队头元素就是 l 指针指向的位置 queue[l]。
-
Rear() 查看队尾：
-
这是最需要注意的地方。因为 r 指向的是下一个将要插入的位置 ，所以真正的队尾元素在 r 的前一个位置。
-
int last = r == 0 ? (limit - 1) : (r - 1);：计算 r 的前一个位置，同样需要考虑环形。如果 r 当前在 0，那么它的前一个位置就是数组的末尾 limit - 1；否则，就是 r - 1。
-
返回 queue[last] 即可。
-
-
isEmpty() 和 isFull()：
- 有了 size 变量，这两个判断变得无比清晰：size == 0 即为空，size == limit 即为满。