1141. 环形链表1 题目
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
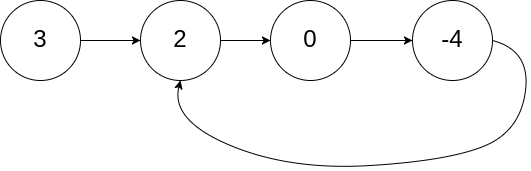
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
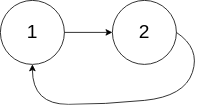
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。示例 3:

输入:head = [1], pos = -1
输出:false
解释:链表中没有环。提示:
- 链表中节点的数目范围是
[0, 104] -105 <= Node.val <= 105pos为-1或者链表中的一个 有效索引 。
进阶: 你能用 O(1)(即,常量)内存解决此问题吗?
2 我的想法
判断环的思想就是,用一个追踪指针从头遍历到尾指针,存在环的意思是:如果在pos所指示的位置有追踪指针,那么追踪指针和尾指针会交汇。
也就是说:
1.如果有环,尾指针指向pos所在节点
2.如果没有环,第一种情况是单个元素,第二种情况是尾指针一定不指向pos所在节点
java
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
}
}难道写一个尾指针.next是否与pos节点一致的判断就好了吗?
具体要怎么实现呢,其实链表对应节点所在val值要是一样的呢?我怎么表示pos节点,我这样的想法可行吗,如何写出合适的java代码?如果是用遍历的话,空间复杂度是O(1),时间复杂度是O(n)对吗?写一个for循环加断?
3 实现
关于你的想法的分析
你提到 "写一个尾指针.next 是否与 pos 节点一致的判断",这个思路存在几个问题:
- pos 不可用 :题目明确说明 pos 是系统内部使用的,不会作为参数传递给我们的函数,所以我们无法直接获取和使用 pos 值
- 尾指针不存在 :在有环的链表中,不存在传统意义上的 "尾指针"(因为链表会循环,没有终点)
- val 值可能重复:如你所担心的,不同节点可能有相同的 val 值,无法通过 val 来判断是否是同一个节点
所以我们需要一种不依赖 pos、不依赖节点值、且空间效率高的方法。
详细解题思路
最经典的解法是 "快慢指针法",也叫 "龟兔赛跑算法",思路如下:
-
指针初始化:
- 定义两个指针,都从链表头部出发
- 慢指针 (slow) 每次只移动 1 步
- 快指针 (fast) 每次移动 2 步
-
核心逻辑:
- 如果链表中没有环:快指针会先到达链表末尾(指向 null)
- 如果链表中有环:两个指针最终一定会在环中相遇
- 因为快指针比慢指针移动得快,进入环后会逐渐追上慢指针
-
终止条件:
- 若快指针到达 null,返回 false(无环)
- 若快慢指针相遇,返回 true(有环)
算法为什么有效?
假设链表存在环,当慢指针刚进入环时,快指针已经在环内某个位置。此时可以看作快指针在追赶慢指针:
- 快指针每次比慢指针多走 1 步
- 相当于慢指针静止,快指针以每秒 1 步的速度追赶
- 只要在环内,快指针最终一定会追上慢指针
java
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
// 处理边界情况:空链表一定没有环
if (head == null) {
return false;
}
// 初始化快慢指针
ListNode slow = head; // 慢指针,每次走1步
ListNode fast = head.next; // 快指针,每次走2步
// 当快慢指针不相等时继续循环
while (slow != fast) {
// 快指针到达末尾,说明没有环
// 注意要先判断fast是否为null,再判断fast.next
if (fast == null || fast.next == null) {
return false;
}
// 慢指针移动1步
slow = slow.next;
// 快指针移动2步
fast = fast.next.next;
}
// 循环结束,说明快慢指针相遇,存在环
return true;
}
}复杂度分析
-
时间复杂度:O (n),其中 n 是链表中的节点数
- 无环情况:快指针会遍历 n/2 个节点就到达末尾
- 有环情况:最坏情况下,两个指针在环中最多遍历 n 个节点就会相遇
-
空间复杂度:O (1),只使用了两个指针,不随链表长度变化,满足题目进阶要求
其他可能的解法(但不满足 O (1) 空间)
-
哈希表法:
- 遍历链表,将每个节点存入哈希表
- 每次访问节点前先检查哈希表,如果已存在则有环
- 空间复杂度 O (n),不满足进阶要求
-
标记法:
- 遍历链表时给每个访问过的节点做标记
- 如果遇到已标记的节点则有环
- 需要修改节点结构,实际中不常用
综上,快慢指针法是解决这个问题的最优解,既高效又节省空间。
4 两种解法
先回顾核心问题:为什么判断链表有环不能靠 "节点值" 或 "pos"?
在理解方法前,先明确两个关键前提(也是你之前担心的点):
- pos 是 "系统内部标记",我们拿不到 :题目里的 pos 只是用来给我们看 "环接在哪",实际写代码时,函数参数只有
head,根本没有 pos 这个值,所以没法用 "尾指针.next == pos 节点" 这种思路。 - 节点值可能重复,不能作为判断依据 :比如链表是
1→2→1→2(有环),两个 "1" 节点值相同,但却是不同节点,靠值判断会误判;反之,不同节点值也可能组成环,所以 "值" 完全不可靠。
这也是为什么我们需要「哈希表」和「快慢指针」这两种不依赖 "值" 或 "pos" 的方法 ------ 它们判断的是 "节点本身是否被重复访问"。
方法一:哈希表法 ------"给走过的节点拍个照,再遇到就是有环"
核心思路:用 "哈希表" 当 "相册",记录所有走过的节点
就像你逛公园时,每经过一个景点就拍张照存手机里。如果逛着逛着,发现眼前的景点 "手机里早就有照片了",说明你绕回了之前的路(有环);如果一直走到公园出口(链表末尾,head == null),都没重复照片,说明没环。
步骤拆解(对应代码)
我们用 Java 的HashSet(哈希表的一种)来实现 "相册",因为HashSet有个特性:添加重复元素时会返回false,这正好帮我们判断 "是否见过这个节点"。
java
public class Solution {
public boolean hasCycle(ListNode head) {
// 1. 初始化哈希表(相册),存的是"节点本身",不是节点值!
Set<ListNode> seen = new HashSet<ListNode>();
// 2. 遍历链表:只要当前节点不为null(没走到出口),就继续走
while (head != null) {
// 3. 尝试把当前节点加入哈希表:
// - 如果添加失败(返回false),说明之前见过这个节点→有环,返回true
// - 如果添加成功,说明是第一次见,继续往下走
if (!seen.add(head)) {
return true;
}
// 4. 移动到下一个节点(逛下一个景点)
head = head.next;
}
// 5. 走出循环说明head == null(走到出口),没环,返回false
return false;
}
}关键细节:为什么存 "ListNode" 而不是 "val"?
- 存
ListNode(节点对象):每个节点对象在内存中都有唯一的 "地址",哈希表判断重复时,比较的是 "地址",能确保 "同一个节点才会被判定为重复"。 - 存
val(节点值):如之前说的,值可能重复,会导致 "不同节点被误判为重复",比如1→2→1(无环),第二个 "1" 会被误判为重复,返回错误的true。
复杂度理解
- 时间复杂度 O (N):最坏情况是 "链表无环",我们要把所有 N 个节点都遍历一遍,每个节点的 "添加" 和 "判断" 操作在哈希表中是 O (1),所以总时间是 O (N)。
- 空间复杂度 O (N):最坏情况是 "链表无环",我们要把 N 个节点都存进哈希表,所以空间是 O (N)------ 这也是它的缺点,不如快慢指针省空间。
方法二:快慢指针法(Floyd 判圈算法)------"让兔子和乌龟赛跑,追上就是有环"
核心思路:用两个速度不同的指针,模拟 "兔子(快)" 和 "乌龟(慢)" 在链表上跑
- 如果链表没环 :兔子跑得比乌龟快,会先跑到链表末尾(
fast == null或fast.next == null),永远追不上乌龟。 - 如果链表有环:兔子会先进入环,然后在环里绕圈;等乌龟也进入环后,兔子因为速度快,总会在某个时刻追上乌龟(两个指针指向同一个节点)。
步骤拆解(对应代码)
先明确指针规则:
- 慢指针(乌龟):每次走 1 步(
slow = slow.next) - 快指针(兔子):每次走 2 步(
fast = fast.next.next)
java
public class Solution {
public boolean hasCycle(ListNode head) {
// 1. 处理边界:空链表(head==null)或只有1个节点(head.next==null),肯定没环
if (head == null || head.next == null) {
return false;
}
// 2. 初始化指针:慢指针从head出发,快指针从head.next出发(关键细节,后面解释)
ListNode slow = head;
ListNode fast = head.next;
// 3. 循环:只要快慢指针没相遇,就继续跑
while (slow != fast) {
// 4. 检查快指针是否到末尾:如果fast或fast.next是null,说明没环
if (fast == null || fast.next == null) {
return false;
}
// 5. 乌龟走1步,兔子走2步
slow = slow.next;
fast = fast.next.next;
}
// 6. 跳出循环→快慢指针相遇,说明有环,返回true
return true;
}
}关键细节 1:为什么初始时快指针要从head.next出发,而不是和慢指针一起从head出发?
这是为了适配while循环的 "先判断,后执行" 逻辑:
- 如果两个指针都从
head出发:初始时slow == fast,while (slow != fast)的条件直接不满足,循环不执行,直接返回false------ 但此时如果链表有环(比如head自己指向自己),就会误判。 - 快指针从
head.next出发:初始时slow = head,fast = head.next,slow != fast,循环能正常开始;即使链表是head自环(head.next = head),第一次循环时:slow会走到head.next = headfast会走到head.next.next = head.next = head- 此时
slow == fast,跳出循环返回true,判断正确。
如果想用 "两个指针都从head出发",可以把while改成do-while(先执行,后判断),代码如下(逻辑完全等价,只是循环方式不同):
java
public boolean hasCycle(ListNode head) {
if (head == null) return false;
ListNode slow = head, fast = head;
// do-while:先移动,再判断是否相遇
do {
// 快指针到末尾,没环
if (fast == null || fast.next == null) return false;
slow = slow.next;
fast = fast.next.next;
} while (slow != fast);
// 相遇,有环
return true;
}关键细节 2:为什么快指针走 2 步,不是 3 步、4 步?
核心是 "快指针速度比慢指针快",走 2 步是最简洁的选择:
- 走 2 步时,每次循环快慢指针的距离会减少 1(比如初始距离 1,下次距离 0;初始距离 2,下次距离 1,再下次距离 0),必然会相遇。
- 走 3 步、4 步也能实现,但代码会更复杂(比如要多判断
fast.next.next是否为 null),且没有性能优势,所以 2 步是最优选择。
复杂度理解
- 时间复杂度 O (N) :
- 无环情况:快指针走 N/2 步就到末尾(因为每次走 2 步),时间 O (N)。
- 有环情况:最坏是 "环很小,乌龟进环前要走很多步",但总体来看,快指针最多绕环 1 圈就能追上乌龟,总步数还是 O (N)。
- 空间复杂度 O (1) :只用到
slow和fast两个指针,不管链表多长,都只占 2 个指针的空间,完全符合题目 "O (1) 内存" 的进阶要求。
两种方法的对比:怎么选?
| 对比维度 | 哈希表法 | 快慢指针法 |
|---|---|---|
| 核心逻辑 | 记录已访问节点,看是否重复 | 速度差导致相遇 |
| 时间复杂度 | O(N) | O(N) |
| 空间复杂度 | O (N)(需要存节点) | O (1)(只需要两个指针) |
| 代码简洁度 | 较简洁(依赖哈希表 API) | 稍复杂(需处理指针初始化) |
| 适用场景 | 除了判断环,还想记录节点 | 只需要判断环,追求省空间 |
实际面试中,快慢指针法是更优的选择------ 因为它满足 O (1) 空间,也是面试官更想考察的思路(能体现对链表特性的深入理解);哈希表法更偏向 "直观思路",适合作为辅助理解的方法。
通过这两个方法的拆解,你应该能彻底明白 "判断链表有环" 的核心逻辑了~ 下次遇到类似问题,不管是用哈希表还是快慢指针,都能清晰地写出代码啦!
【解释:if (!seen.add(head))】
我们来详细解释一下你看不懂的这行代码:if (!seen.add(head))
这句话的作用
这句话的意思是:尝试把当前节点head添加到哈希表seen中,如果添加失败(说明这个节点已经在哈希表中存在了),就返回true(表示有环)
逐步拆解
-
seen是一个HashSet<ListNode>类型的集合,用来存储我们已经访问过的节点 -
seen.add(head)这个方法的特性:- 当我们往 HashSet 中添加元素时,如果这个元素之前不存在 ,就会添加成功,返回
true - 如果这个元素之前已经存在 ,就会添加失败,返回
false
- 当我们往 HashSet 中添加元素时,如果这个元素之前不存在 ,就会添加成功,返回
-
!是逻辑非运算符,用来取反:- 如果
seen.add(head)返回true(添加成功,是新节点),那么!true就是false,不会进入 if 语句 - 如果
seen.add(head)返回false(添加失败,节点已存在),那么!false就是true,会进入 if 语句,执行return true
- 如果
举个生活化的例子
这就像我们去游乐园玩,每个景点门口有个登记簿:
- 第一次到某个景点,我们在登记簿上写下名字(添加成功),继续游玩
- 如果走到一个景点,发现登记簿上已经有我们的名字了(添加失败),说明我们绕了一圈又回到了曾经去过的地方,这就证明游乐园的路线是环形的
整个代码的逻辑流程
- 从头节点开始遍历链表
- 每到一个节点,就尝试把它加入哈希表
- 如果添加失败(节点已存在),说明有环,返回
true - 如果添加成功,就继续访问下一个节点
- 直到遍历完所有节点(
head == null),说明没有环,返回false
这样通过哈希表记录访问过的节点,就能判断链表是否存在环了,是不是很容易理解呢?