机器学习shap分析案例

    在进行数据分析和机器学习时经常用到shap，本文对shap相关的操作进行演示。波士顿数据集链接在这里。

SHAP Analysis Guide

Set up

导入必要包

import pandas as pd
import numpy as np
import lightgbm as lgb
import matplotlib
import matplotlib.pyplot as plt
import shap
import seaborn as sns
import warnings

plt.style.use("style.mplstyle")

Load Data

数据集原始论文
关于特征B

import pandas as pd

# 读取 txt 文件
file_path = "shap/boston.txt"  # 替换为你的文件路径
with open(file_path, "r") as file:
    lines = file.readlines()

# 初始化空列表存储数据
data = []

# 按两行一组处理数据
for i in range(0, len(lines), 2):
    # 第一行：前 11 个数据点
    row1 = list(map(float, lines[i].strip().split()))
    # 第二行：后 3 个数据点
    row2 = list(map(float, lines[i + 1].strip().split()))
    # 将两行合并为一组完整数据（共 14 个数据点）
    data.append(row1 + row2)

# 定义列名
columns = [
            "crime rate",
            "% residential zone",
            "% industrial zone",
            "Charles River",
            "NOX concentration",
            "number of rooms",
            "% built before 1940",
            "remoteness",
            "connectedness",
            "tax rate",
            "pupil-teacher ratio",
            "B",
            "% working class",
            'target'
]

# 转换为 DataFrame
df = pd.DataFrame(data, columns=columns)

# 查看数据
print(df.head())

可视化部分数据

删除特征B

# 删除 "B" 列
df = df.drop("B", axis=1)

练习修改数据

# 修改数据（例如将 "% working class" 列乘以 2）
df["% working class"] = df["% working class"] * 2
df['target'] = df['target'] * 1000
X = df.drop("target", axis=1).copy()
# 查看处理后的数据
print(df.head())

打印房间预测值

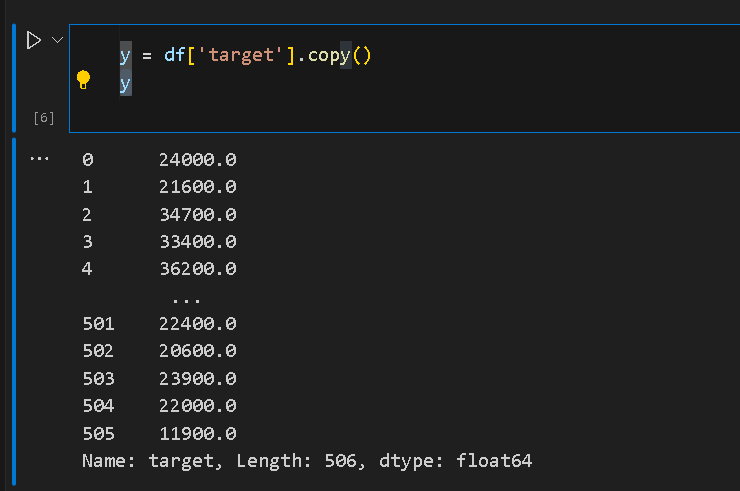
保存经过处理后的数据集

df.to_csv("shap/data.csv", index=False)

打印据相关的数值信息

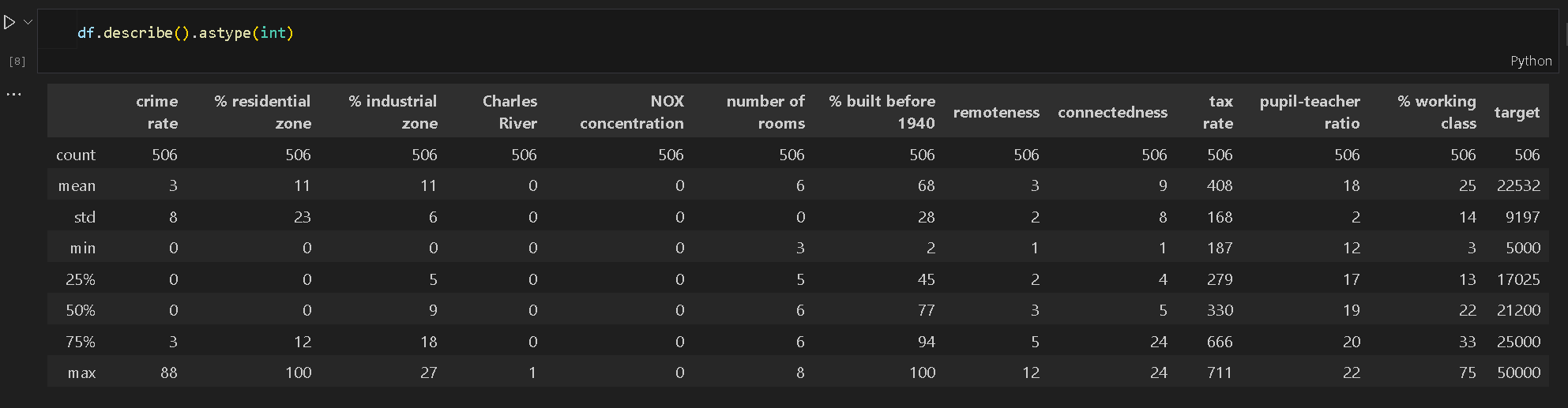
修改字体(可选)

# 设置字体为系统支持的字体
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['Arial', 'DejaVu Sans', 'Liberation Sans', 'Helvetica']

数据分布可视化

fig, axs = plt.subplots(ncols=5, nrows=3, figsize=(14, 9))
gs = axs[1, 2].get_gridspec()
for ax in axs[:, -1]:
    ax.remove()
axbig = fig.add_subplot(gs[:, -1])
axs = axs.flatten()

for col, i in zip(X.columns, [0, 1, 2, 3, 5, 6, 7, 8, 10, 11, 12, 13]):
    axs[i].hist(X[col])
    axs[i].set_xlabel(col, size=16)
    axs[i].grid()
    axs[i].set_ylim(0, 490)

d = df.copy()
d["house price"] = df["target"]
sns.boxplot(y=d["house price"], color="#d45087")
axbig.set_yticklabels(axbig.get_yticks(), rotation=45)
axbig.get_yaxis().set_major_formatter(
    matplotlib.ticker.FuncFormatter(lambda x, p: format(int(x), ","))
)
axbig.set_xlabel("house price ($)")
axbig.set_ylabel("")
axbig.grid(axis="y")

fig.subplots_adjust(hspace=0.5)
fig.text(-0.01, 0.5, "count of instances", va="center", rotation="vertical", size=20)
fig.tight_layout()
fig.show()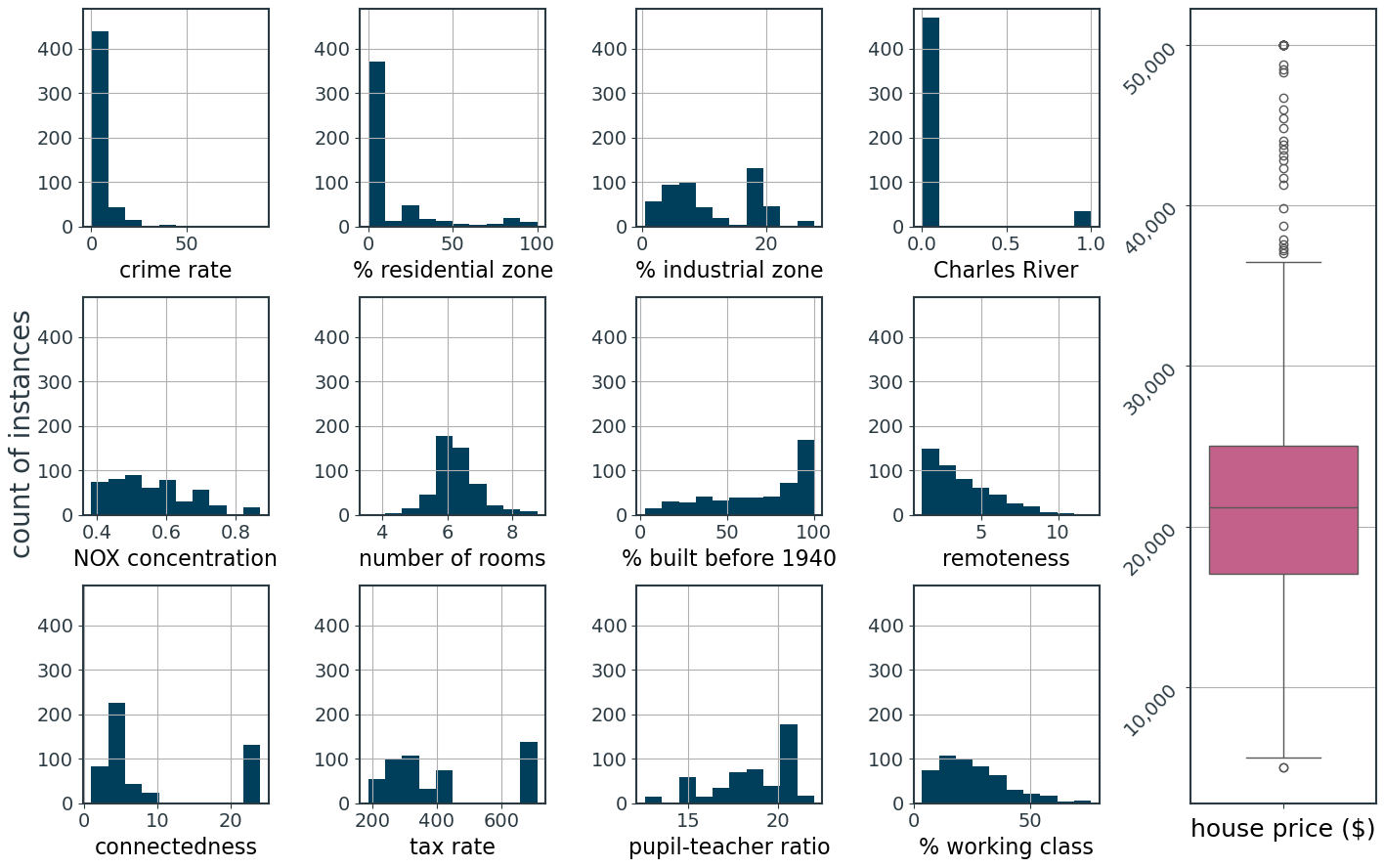

Train Model

训练一个LGBM模型

m = lgb.LGBMRegressor()
m.fit(X, y)

预测并评估模型

Compute SHAP Values

explainer = shap.Explainer(m)
shap_values = explainer(X)

打印数据维度，可以看出shap值的维度与原始数据的维度相同

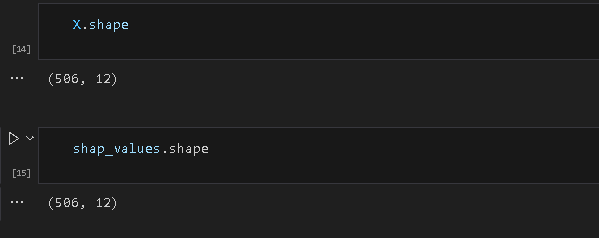
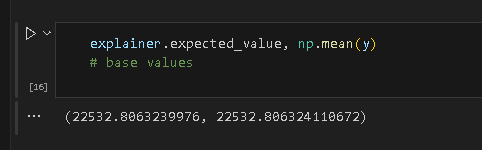
在 SHAP 的回归场景下，base value 等于模型对训练集预测结果的期望

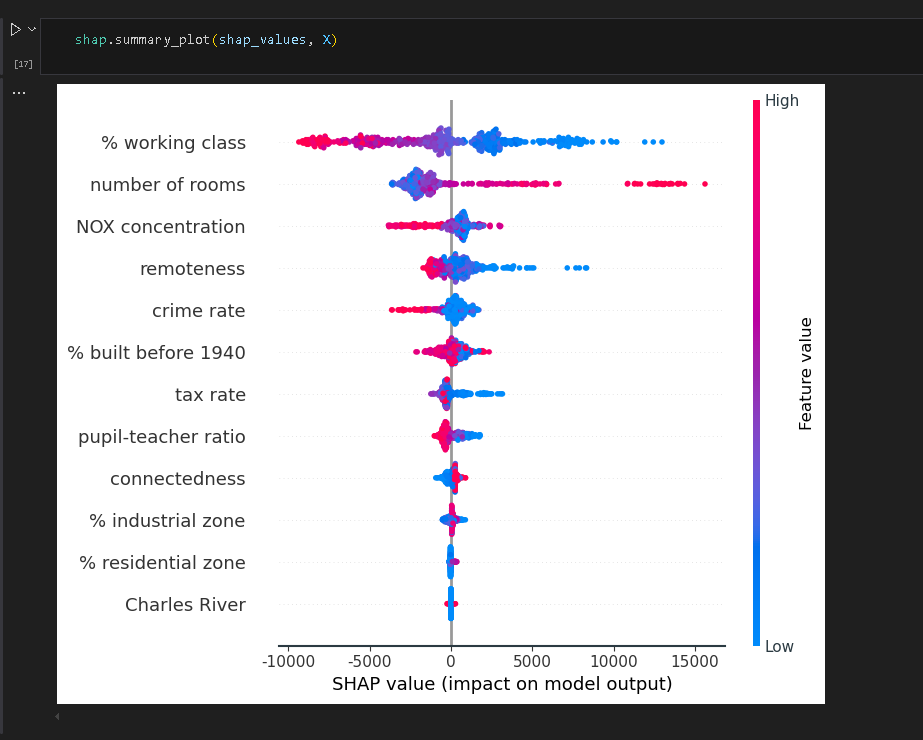
绘制shap分析图

下图是第一种图，蜂巢图也是summary图，信息最多。红色表示数值大，蓝色表示数值小，点的密集程度表示数据的分布。特征的重要性从上到下排序，横轴左侧表示负相关，右侧表示正相关。

计算分位点

i_med = np.argsort(y_pred)[len(y_pred)//2]
i_max = np.argmax(y_pred)
i_80 = np.argsort(y_pred)[int(len(y_pred)*0.8)]
i_60 = np.argsort(y_pred)[int(len(y_pred)*0.6)]
i_40 = np.argsort(y_pred)[int(len(y_pred)*0.4)]
i_20 = np.argsort(y_pred)[int(len(y_pred)*0.2)]
i_min = np.argmin(y_pred)

下面是第二种图，瀑布图，可以展示不同特征对最终预测结果具体的影响。

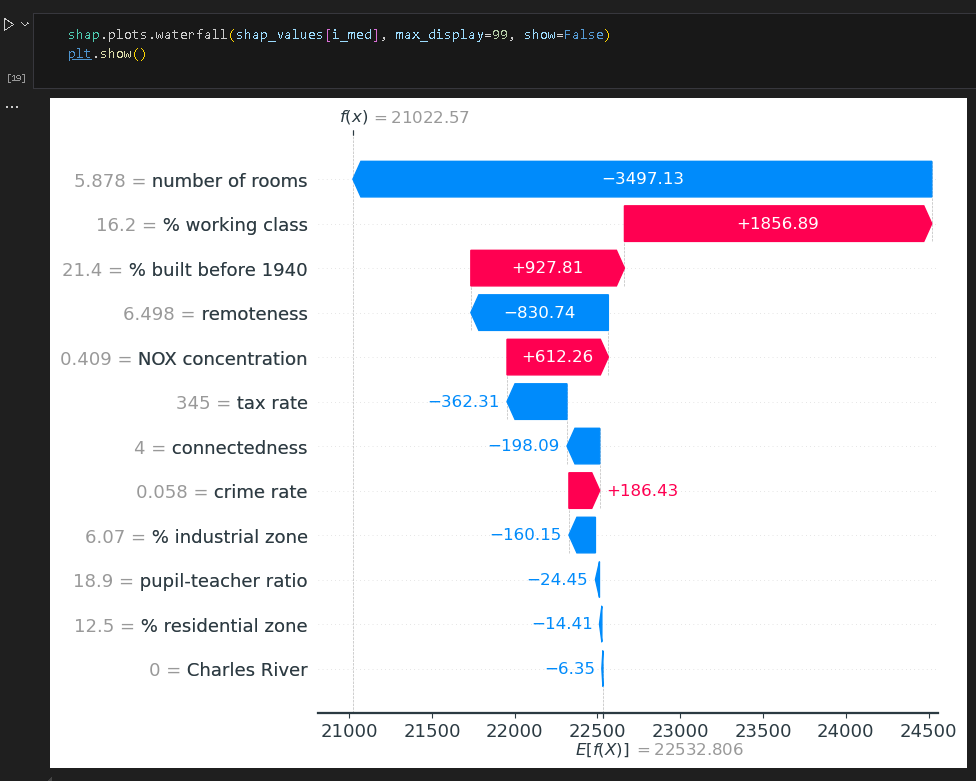
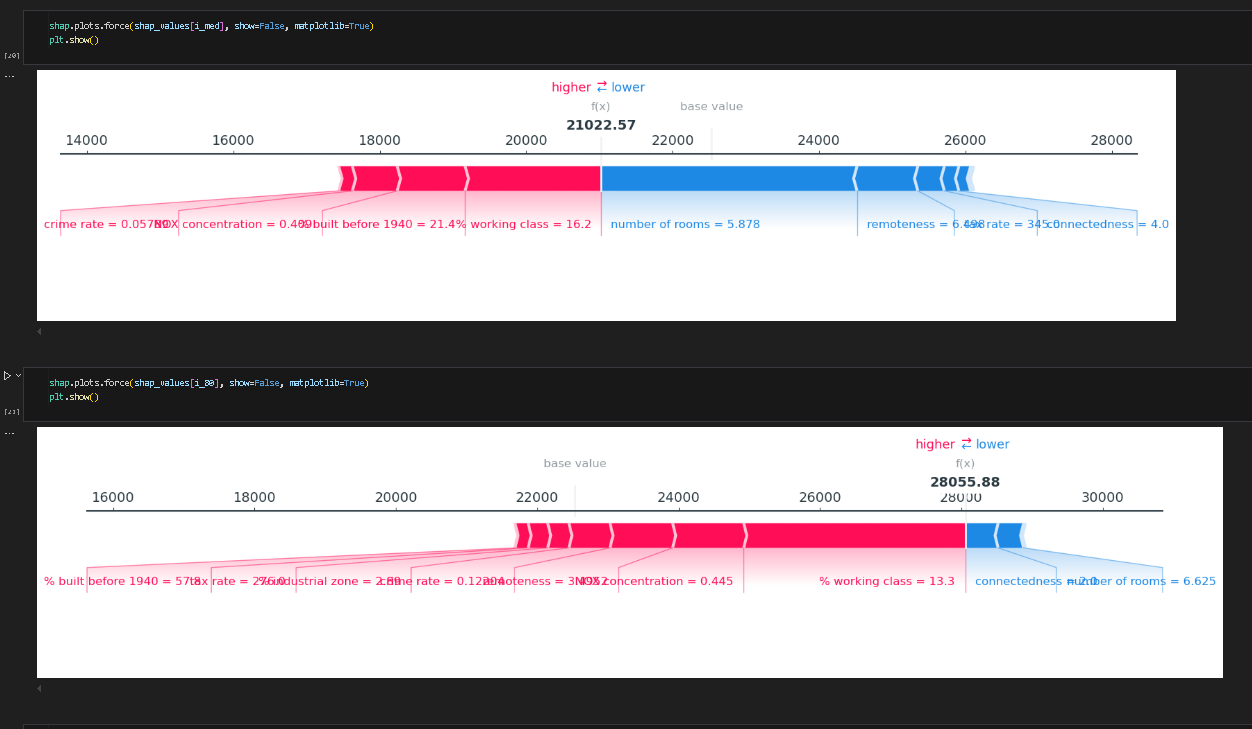
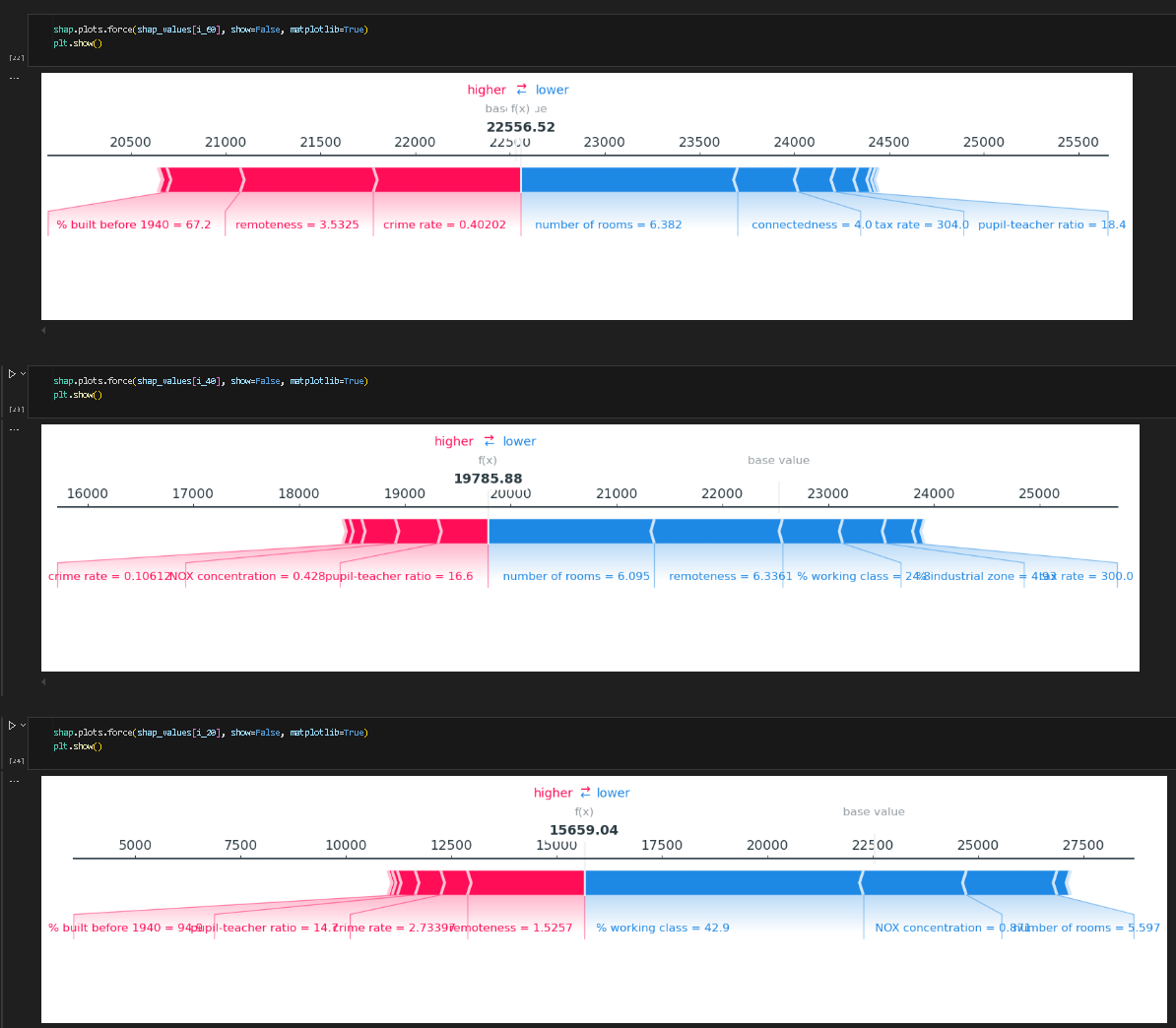
下图展示了力图，红色越长表示正向作用力越强，模型预测越偏大，反之蓝色会让模型预测偏小。

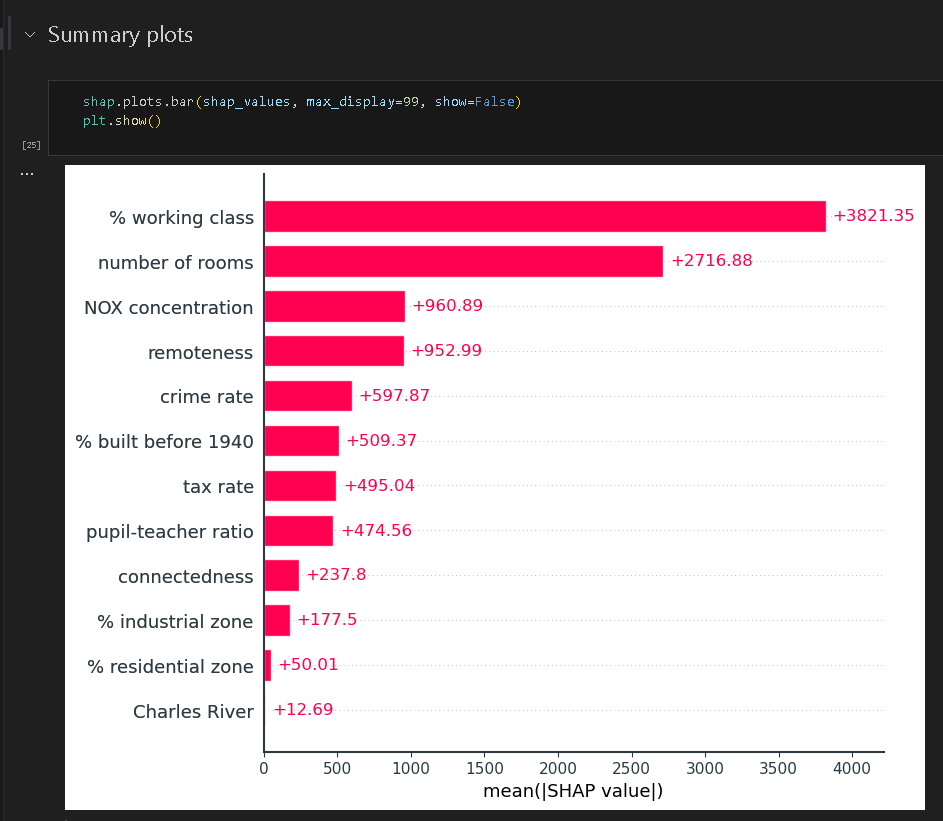
下面是条状图，横轴表示shap值绝对值的平均值，展示了每一种特征对最终结果的影响程度。

值得注意的是，shap相关的api也是可以进行更改的，用户可以按照自己的喜好更改api进行绘图。如下所示，可以人为的绘制出条状图，并可以将蜂巢图的输出转化成绝对值的形式。

plt.subplot(2, 1, 1)
# plt.gcf()
shap.plots.bar(shap_values.abs.max(0), max_display=99, show=False)
plt.subplot(2, 1, 2)
shap.plots.beeswarm(
    shap_values.abs, color="shap_red", max_display=99, show=False, plot_size=None
)
ax = plt.gca()
masv = {}
for feature in ax.get_yticklabels():
    name = feature.get_text()
    col_ind = X.columns.get_loc(name)
    mean_abs_sv = np.mean(np.abs(shap_values.values[:, col_ind]))
    masv[name] = mean_abs_sv
ax.scatter(
    masv.values(),
    [i for i in range(len(X.columns))],
    zorder=99,
    label="Mean Absolute SHAP Value",
    c="k",
    marker="|",
    linewidths=3,
    s=100,
)
ax.legend(frameon=True)
plt.tight_layout()
plt.show()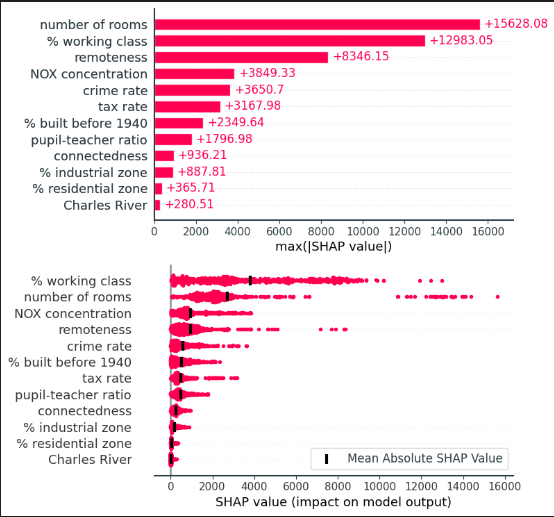

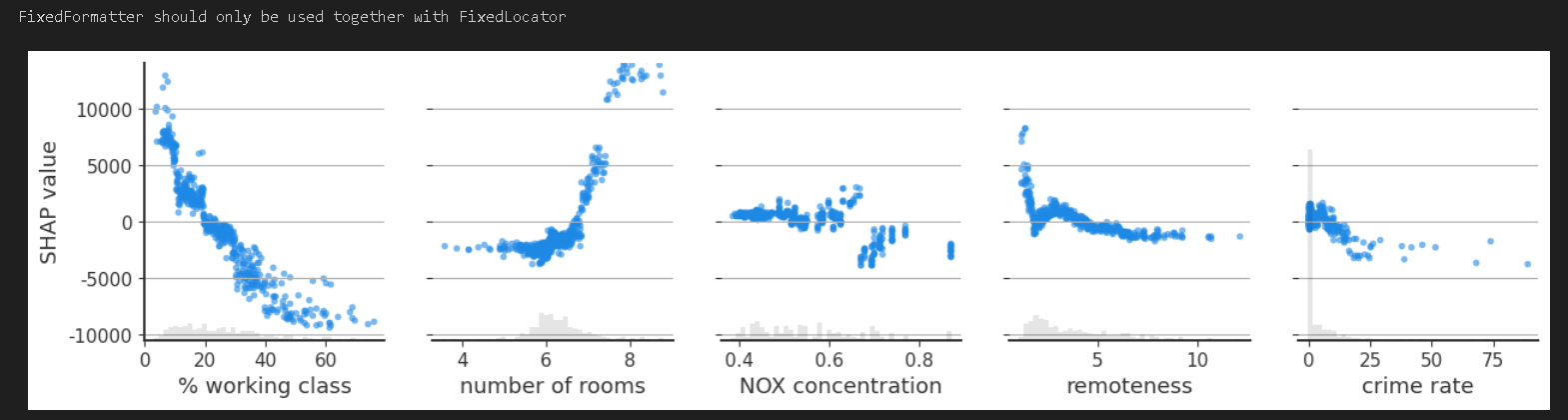
下图展示的是依赖图

n = 5
fig, ax = plt.subplots(1, n, figsize=(15, 3))

for i, (k, v) in enumerate(sorted(masv.items(), key=lambda x: x[1], reverse=True)):
    if i < n:
        shap.plots.scatter(shap_values[:, k], ax=ax[i], show=False, alpha=0.6)
        ax[i].grid(axis="y")
        if i != 0:
            ax[i].set_ylabel("")
            ax[i].spines["left"].set_visible(False)
            ax[i].set_ylim(ax[0].get_ylim())
            ax[i].set_yticklabels(["" for _ in range(len(ax[0].get_yticks()))])
        else:
            ax[i].set_ylabel("SHAP value")
plt.show()

以前5个特征为例，可以看出每个特征和shap值之间的关系，图一图二可以看出比较明显的线性关系。图四表示距离较近时也有一定的线性关系，但是随着距离增加以后就线性无关了。

下面展示最后一种散点图，会自动给出对当前特征(工薪阶级)相互作用强的特征作为颜色依据。可以明显的看出，工薪阶级百分比与自身 SHAP 值呈显著负相关，并且工薪阶级占比越大，NOX的排放浓度也越大，房价也越低；反之，工薪阶级占比少，NOX浓度高，房价也高。

fig, ax = plt.subplots()
shap.plots.scatter(shap_values[:, "% working class"], color=shap_values, ax=ax)
plt.show()