CUDA常规知识点

参考: mp.weixin.qq.com/s/wIiyrMaTJ...

👉 ThreadsPerBlock和Blocks的数量受哪些条件约束？

1. 硬件限制（上限）

(1) 线程与块维度约束

每个 Block 的最大线程数：

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ThreadsPerBlock ≤ maxThreadsPerBlock \text{ThreadsPerBlock} \le \text{maxThreadsPerBlock} </math>ThreadsPerBlock≤maxThreadsPerBlock

（通过 cudaGetDeviceProperties 查询 maxThreadsPerBlock）

Grid 的 Block 维度上限：

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> GridDim x ≤ maxGridSize [ 0 ] , GridDim y ≤ maxGridSize [ 1 ] , GridDim z ≤ maxGridSize [ 2 ] \begin{align*} \text{GridDim}_x &\le \text{maxGridSize}[0], \\ \text{GridDim}_y &\le \text{maxGridSize}[1], \\ \text{GridDim}_z &\le \text{maxGridSize}[2] \end{align*} </math>GridDimxGridDimyGridDimz≤maxGridSize[0],≤maxGridSize[1],≤maxGridSize[2]

(2) SM 资源约束

每个 SM 的最大 Block 数：
<math xmlns="http://www.w3.org/1998/Math/MathML"> BlocksPerSM ≤ maxBlocksPerMultiProcessor \text{BlocksPerSM} \le \text{maxBlocksPerMultiProcessor} </math>BlocksPerSM≤maxBlocksPerMultiProcessor
每个 SM 的最大线程数：
<math xmlns="http://www.w3.org/1998/Math/MathML"> BlocksPerSM × ThreadsPerBlock ≤ maxThreadsPerMultiProcessor \text{BlocksPerSM} \times \text{ThreadsPerBlock} \le \text{maxThreadsPerMultiProcessor} </math>BlocksPerSM×ThreadsPerBlock≤maxThreadsPerMultiProcessor
共享内存限制：
<math xmlns="http://www.w3.org/1998/Math/MathML"> SharedMemUsedPerBlock ≤ sharedMemPerBlock \text{SharedMemUsedPerBlock} \le \text{sharedMemPerBlock} </math>SharedMemUsedPerBlock≤sharedMemPerBlock
寄存器限制：
<math xmlns="http://www.w3.org/1998/Math/MathML"> RegsPerThread × ThreadsPerBlock ≤ maxRegistersPerBlock \text{RegsPerThread} \times \text{ThreadsPerBlock} \le \text{maxRegistersPerBlock} </math>RegsPerThread×ThreadsPerBlock≤maxRegistersPerBlock

可通过编译选项 -maxrregcount 指定线程寄存器数上限）

2. 算法/问题需求（下限与结构）

线程总数要求：

<math xmlns="http://www.w3.org/1998/Math/MathML"> TotalThreads ≥ DataSetSize \text{TotalThreads} \ge \text{DataSetSize} </math>TotalThreads≥DataSetSize （覆盖完整数据集）
Block 数量要求：

<math xmlns="http://www.w3.org/1998/Math/MathML"> GridSize ≥ SMCount × BlocksPerSM \text{GridSize} \ge \text{SMCount} \times \text{BlocksPerSM} </math>GridSize≥SMCount×BlocksPerSM（充分利用所有 SM）
线程组织：

维度结构（1D/2D/3D）需匹配数据访问模式（如合并内存访问）
特殊优化需求：

<math xmlns="http://www.w3.org/1998/Math/MathML"> ThreadsPerBlock \text{ThreadsPerBlock} </math>ThreadsPerBlock 需为 WarpSize的倍数（避免资源浪费）

👉 理论计算占用率公式

占用率（Occupancy） 定义为 SM 中活跃 Warp 数与最大支持 Warp 数的比例：

分量计算

每个 Block 的 Warp 数：
每个 SM 的活跃 Warp 数：
每个 SM 的最大 Warp 数：

关键说明

实际限制：
受线程数、共享内存、寄存器等资源约束。
性能权衡：
100%占用率非绝对最优，有时需降低占用率以换取更高寄存器用量或减少 Bank Conflict。
工具支持：
可通过 cudaOccupancyMaxActiveBlocksPerMultiprocessor 或 Nsight Compute 预测/实测占用率。

公式应用示例

假设：

GPU 的 maxThreadsPerMultiProcessor = 2048，WarpSize = 32
Kernel 配置：ThreadsPerBlock = 256 ，则：
- 若资源允许每个 SM 驻留 8 个 Block（即），则：
  <math xmlns="http://www.w3.org/1998/Math/MathML"> M a x W a r p s P e r S M = 2048 32 = 64 ; W a r p s P e r B l o c k = ⌈ 256 32 ⌉ = 8 MaxWarpsPerSM = \frac{2048}{32} = 64; WarpsPerBlock = \left \lceil \frac{256}{32} \right \rceil = 8 </math>MaxWarpsPerSM=322048=64;WarpsPerBlock=⌈32256⌉=8
- 若资源允许每个 SM 驻留 8 个 Block（即 BlocksPerSM = 8）, 则：
  <math xmlns="http://www.w3.org/1998/Math/MathML"> A c t i v e W a r p s P e r S M = 8 × 8 = 64 ; O c c u p a n c y = 64 64 = 100 % ActiveWarpsPerSM = 8 \times 8 = 64; Occupancy = \frac{64}{64} = 100 \% </math>ActiveWarpsPerSM=8×8=64;Occupancy=6464=100%

👉 CUDA汇编-PTX与SASS

PTX (Parallel Thread eXecution)：
虚拟指令集（类似汇编）
- 跨平台（nvcc -ptx生成）
SASS (Streaming ASSembly)：
真实GPU机器码（架构相关）
- 通过 cuobjdump --dump-sass 反汇编
关系：
CUDA C/C++ → PTX → (JIT编译) → SASS → GPU执行

通常称PTX 是高层次汇编，而SASS是低层次汇编

👉 浮点格式对比

格式	位宽	指数位	应用场景
FP32	32-bit	8-bit	通用计算
TF32	19-bit	8-bit	Ampere矩阵乘法
FP16	16-bit	5-bit	AI训练/推理
BF16	16-bit	8-bit	替代FP32 (范围保留)

👉 CUDA的内存模型

CUDA的内存模型Memory类型

内存类型	位置	延迟	带宽	作用域
寄存器	片内	1 cycle	∞	线程私有
共享内存	片内	~20 cycles	高	Block共享
L1缓存	片内	~30 cycles	高	SM私有
L2缓存	片内	~200 cycles	中	GPU全局
全局内存	片外	200-400 cycles	中高	所有线程
常量内存	片外+缓存	广播:快随机:慢	变	只读
纹理内存	片外+缓存	空间局部性优	中	特殊访问

Global memory的访存合并

定义： Global Memory 访存合并 (Coalesced Access) 是指同一个Warp内的多个线程 对连续的、对齐的Global Memory地址 的访问请求，被硬件合并成一个或少量的内存事务 (Memory Transaction) 来处理的技术。
目的： 最大化Global Memory带宽利用率，减少内存访问次数，隐藏高延迟。
要求 (理想情况)：
- 连续性 (Contiguous): Warp中第T个线程访问地址BaseAddress + T * sizeof(type)。
- 对齐 (Aligned): 合并访问的起始地址通常是32字节、64字节或128字节对齐的 (取决于架构和事务大小)。
- 级别：访问能被合并成32字节、64字节、128字节的事务。访问模式越连续、越对齐，合并效果越好，使用的内存事务越少。
- 未合并访问的后果：一个Warp的访问可能被拆分成多个（最多32个！）独立的小内存事务，极大浪费带宽并显著增加延迟。

如何实现：
- 确保线程访问的数据在Global Memory中是连续存储的 (数组结构体SoA优于结构体数组AoS)。
- 确保线程的索引threadIdx.x对应于访问地址的低位连续部分。
- 使用合适的数据类型和对齐属性 (__align__或cudaMallocPitch/cudaMalloc3D用于2D/3D数据)。

寄存器(Register)与本地内存(Local Memory)的变量分配规则

寄存器分配条件
- 标量局部变量（如 int i）
- 小型数组（索引编译时确定）
- 未超出寄存器限制（通过 --maxrregcount 控制）
Local Memory分配条件：
- 大型数组或动态索引数组
- 寄存器溢出（变量过多/复杂）
- 取地址操作的变量（如 &local_var）
关键区别：寄存器访问延迟≈1 cycle，Local Memory访问延迟≈200~400 cycles（需经L1/L2缓存）

👉 Bank Conflict 的优化方案

Bank Conflict 本质

当同一个Warp内的多个线程访问同一Bank（主要是shared memory）的不同地址。
后果：访问请求被串行化，性能急剧下降
检测指标 ：shared_ld_bank_conflict 和 shared_st_bank_conflict（Nsight Compute）

避免方案（16种专业技巧）

类别	方案	适用场景	示例
布局优化	1. 地址偏移	矩阵访问	`arr[tid][col + 1]`（添加1列padding）
	2. 存储转置	行列访问转换	行列索引交换：`arr[col][row]` → `arr[row][col]`
	3. Z-order曲线	2D/3D数据结构	`index = (row * 32) ^ col`（Morton编码）
数据格式	4. Bank对齐	64位数据访问	使用`__shared__ double`替代两个`float`
	5. 压缩存储	16位数据类型	将两个FP16打包为`uint32_t`存储
访问模式	6. 广播优化	常量/共享值读取	所有线程读取`shared_data[0]`
	7. SIMD向量访问	连续数据加载	`float4 vec = reinterpret_cast<float4>(&data[tid*4])`
	8. 交错存储	多维数据	物理行号 = `(row%4)*32 + row/4`
算法优化	9. 归约树重构	并行归约操作	步长2访问：`sdata[tid2] += sdata[tid2 + stride]`
	10. Bank感知扫描	前缀和计算	奇偶分离扫描算法
动态调整	11. 动态偏移	多Block协作	`index = (tid*4 + blockIdx.x%16) % size`
	12. Warp旋转	Warp间数据交换	`rotated_id = (tid + warp_id) % 32`
高级技术	13. Bank重映射	复杂访问模式	自定义映射表：`remap_table[8] = {0,5,2,7,4,1,6,3}`
	14. 双缓冲隔离	流水线处理	`bufferA[128+2]`使用中间区域`[1..128]`
	15. 比特反转索引	随机访问优化	`index = __brev(tid) >> 27`（5位反转）
终极方案	16. Bank冲突免疫	极端敏感场景	按Bank分组序列化写入

👉 CUDA程序的调度和计算单元

Block在SM上的调度执行机制

资源分配：

SM检查Block所需的资源（线程数/共享内存/寄存器）
资源充足则分配Slot（最大Block数由架构决定，如Ampere为16/SM）

Warp调度：

Block被划分为Warps（32线程组）
Warp Scheduler按周期发射指令（如Volta每SM4个调度器）

延迟隐藏：

当Warp等待内存时，SM立即切换其他就绪Warp
需满足：Active Warps >= 延迟周期 / 切换开销（通常需20+ Warps/SM）

CUDA Core vs Tensor Core

特性	CUDA Core	Tensor Core
计算粒度	标量运算	矩阵乘法累加（MMA）
典型操作	FP32/INT32标量计算	4x4 FP16矩阵乘
吞吐量	1 OP/cycle/core	64 FP16 FMA/cycle/core
架构支持	所有GPU	Volta及更新架构

GPU分支预测与指令级并行

分支预测

GPU 上的分支预测非常有限，不是主要的优化手段；不支持复杂分支预测器。通过Warp内所有线程执行所有分支路径（Divergence开销大）

指令级并行(ILP)

流水线并行：指令分成取指/解码/执行等阶段
多发射机制：Volta+架构支持每周期发射2条独立指令
依赖消除：编译器重排指令避免停顿

🟢 GPU 如何实现 ILP？

GPU 没有传统意义上的单线程乱序执行！

但它有另一种形式的 ILP，称为：

"隐式指令级并行"（Implicit ILP via Multi-Warp Scheduling）

✅ 核心机制：

每个 SM 可以同时驻留多个 warp（几十个）。
当一个 warp 因内存访问、长延迟指令（如除法）而阻塞时，Warp Scheduler 会立即切换到另一个就绪的 warp 执行其下一条指令。
对于 GPU 来说，这种"上下文切换 "发生在一个时钟周期内，几乎无开销。

🫆分支发散（branch divergence）

GPU 中线程以 warp（32 线程） 为单位执行。
同一个 warp 中 的所有线程必须同时执行同一条指令（Single Instruction, Multiple Threads）。
如果 warp 内部线程对某个 if 条件判断结果不同 → 发生分支发散（Branch Divergence）， 由原本的一次并行执行 --> 至少两次以上的串行执行。

有 `if` 的问题示例：

ini 复制代码

__global__ void kernel(float* data, float* result) {
    int idx = blockIdx.x * blockDim.x + threadIdx.x;
    // 假设 warp 中的32个线程 一半 >0，一半 <=0
    if (data[idx] > 0.0f) {
        result[idx] = sqrt(data[idx]);
    } else {
        result[idx] = 0.0f;
    }
}

⚠️ 执行过程

Warp 中有 16 个线程满足 data[idx] > 0，另外 16 个不满足。
GPU 执行引擎：

先执行 if 分支（计算 sqrt），但屏蔽掉那 16 个不满足条件的线程 → 它们空转；
再执行 else 分支（赋值 0），但屏蔽掉那 16 个满足条件的线程 → 它们也空转。

结果：原本可以并行执行的 32 个线程，变成了串行执行两遍 16 个线程 → 性能下降接近 50%！

🔥 这就是分支发散的代价：浪费了 50% 的计算资源！

使用"掩码"用它代替 `if`

🎯 掩码（Mask）的本质：

用布尔运算 + 数学表达式代替条件判断，让所有线程都执行相同路径，只是通过"乘法开关"控制是否生效。

✅ 改写示例（用掩码代替 if）：

cpp 复制代码

__global__ void kernel(float* data, float* result) {
   int idx = blockIdx.x * blockDim.x + threadIdx.x;

   // 生成掩码：满足条件为 1.0，否则为 0.0
   float mask = (data[idx] > 0.0f) ? 1.0f : 0.0f;

   // 用数学方式合并结果：无分支！
   result[idx] = mask * sqrtf(data[idx]) + (1.0f - mask) * 0.0f;
}

💡 效果分析：

所有 32 个线程都执行 sqrtf(data[idx]) 和比较操作；
但那些不满足条件的线程，其结果被乘以 0，最终输出为 0；
没有分支发散！所有线程同步执行相同指令！
性能提升显著：从 50% 利用率 → 100% 利用率！
⚠️ 虽然 line5 使用了三元条件表达式 ?:，看起来像 if...else... ，但是 GPU 编译器会对其进行优化，编译成无分支的纯算术/位操作指令，而不是条件跳转，所以不会产生分支发散。

Float/Int指令周期与融合操作

指令延迟对比（Ampere架构）

指令类型	操作	吞吐量（每SM每周期）	延迟（周期）
FP32 FMA	`a*b + c`	128	4
FP32 ADD	`a + b`	128	4
FP32 MUL	`a * b`	128	4
INT32 ADD	`a + b`	256	1
INT32 MUL	`a * b`	64	10
FP16 FMA	`a*b + c`	512	2
INT8 DP4A	4元素点积	1024	4

融合操作示例

cpp 复制代码

// FP32 乘加融合（单指令）：
float fma = a * b + c;  // 生成FFMA指令（4周期）

// INT32 无融合（多指令）：
int mul_add = a * b + c; // 分解为IMUL(10周期) + IADD(1周期)

// FP16 矩阵乘融合（Tensor Core）：
__hmma_m16n16k16_fma(a, b, c); // 单指令完成16x16x16矩阵乘加

👉 Roofline模型及计算优化

Roofline Model 深度解析

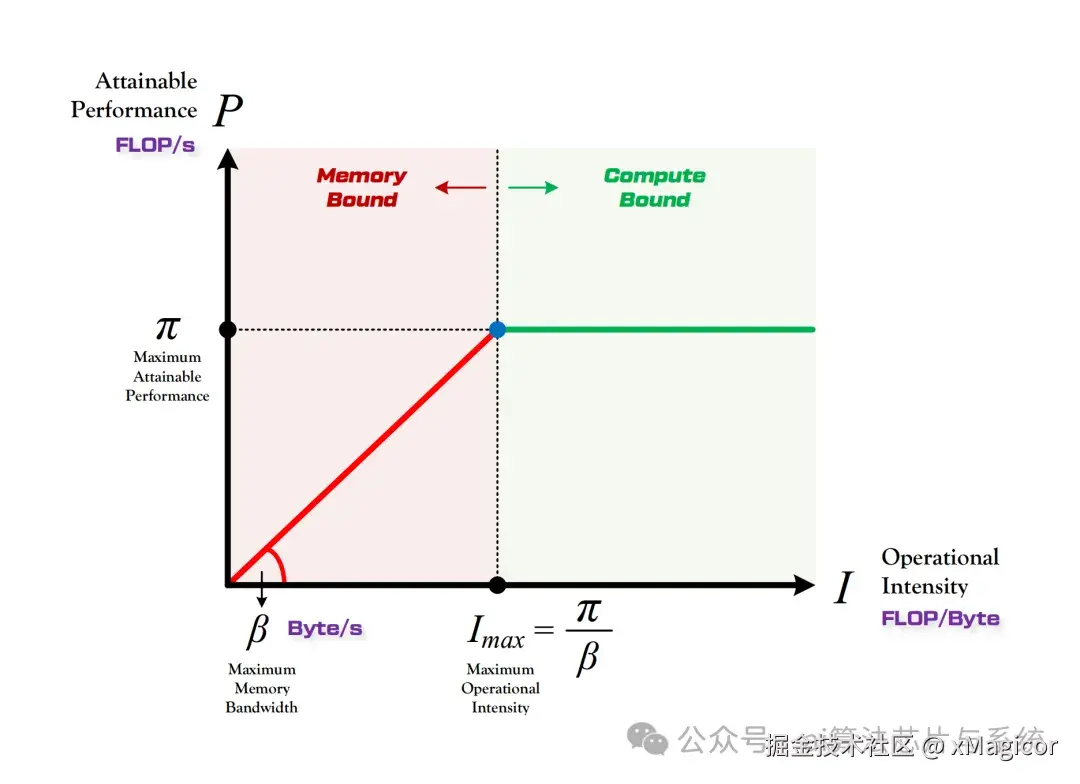Roofline Model

X 轴：计算强度（Arithmetic Intensity，单位：OPs/Byte）。
Y 轴：可达性能（GFLOPs），此可达性能对于不同的数据类型不同，比如float和int的可达性能不同，并且和使用的计算单元相关，比如使用或者不使用simd。
屋顶线：由内存带宽（斜线）和算力峰值（水平线）构成。

模型核心要素

关键参数计算

计算强度 (Arithmetic Intensity) AI = 总操作数（FLOPs）/ 总字节数（Bytes）
理论性能峰值

ini 复制代码

Peak Perf = min(
    内存带宽 × 计算强度,
    硬件算力峰值
)

1. 实际性能测量

bash 复制代码

# 获取FLOPs
ncu --metrics smsp__sass_thread_inst_executed_op_fadd_pred_on,smsp__sass_thread_inst_executed_op_fmul_pred_on,smsp__sass_thread_inst_executed_op_ffma_pred_on ./app

# 获取字节数
ncu --metrics dram__bytes_read.sum,dram__bytes_write.sum ./app

优化决策树

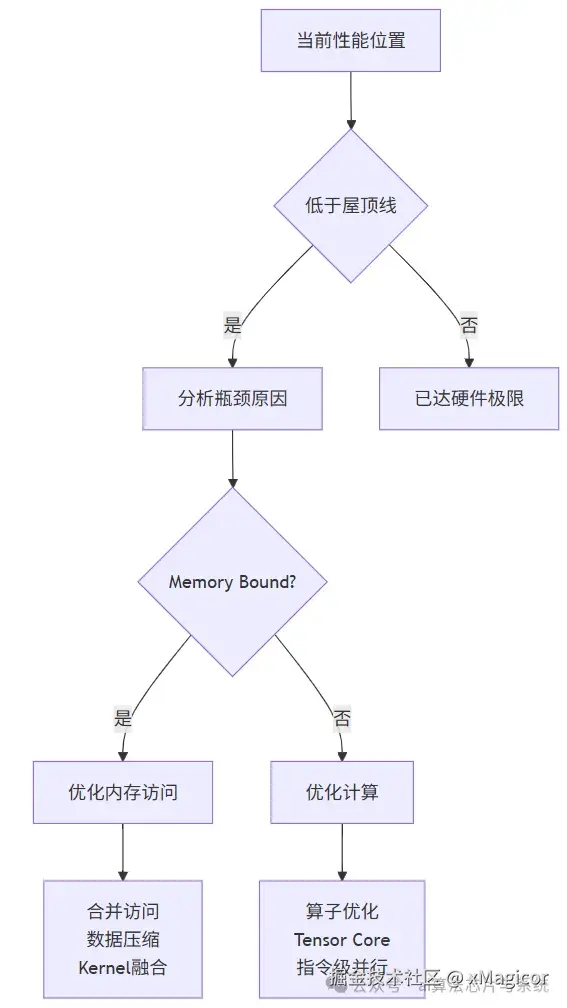
典型场景优化策略

区域	特征	优化策略
内存瓶颈区	低计算强度 (<10 FLOP/Byte)	• Global Memory合并访问 • 共享内存Bank优化 • 数据压缩（FP16/BF16） • Kernel融合减少数据搬运
计算瓶颈区	高计算强度 (>100 FLOP/Byte)	• 算子优化（循环展开/指令选择） • Tensor Core利用 • 增加ILP（指令级并行） • 降低精度（FP32→TF32）
过渡区	中等计算强度 (10-100)	• 双缓冲技术 • 数据分块计算 • 混合精度计算

Kernel Fusion的优势与示例

核心原理与工作机制

传统多Kernel执行的瓶颈
- Kernel Launch开销：每次启动一个CUDA kernel需6--10μs，频繁启动小kernel时，该开销占比显著。
- 全局内存（Global Memory）访问：每个kernel需将中间结果写入全局内存，后续kernel再读取，导致高延迟和带宽压力。
Fusion的优化逻辑
- 合并计算逻辑：将多个操作（如逐元素乘法 + 求和）合并为一个kernel，避免中间结果写回全局内存，改用寄存器或共享内存暂存数据。
- 减少Launch次数：多个操作仅需一次kernel启动。

核心优势

降低延迟与带宽压力

数据在寄存器或共享内存中直接传递，减少全局内存访问次数，提升计算效率。
例如：向量点积中，融合乘法和求和可避免中间结果写回。

隐藏Kernel Launch开销

对执行时间短的kernel（如深度学习中的小算子），融合后性能提升显著（20--50%）。

提升硬件利用率

通过合并无数据依赖的kernel（Horizontal Fusion），并行执行独立任务，提高SM（流多处理器）资源利用率。

技术实现方式

垂直融合（Vertical Fusion）

合并具有数据依赖的连续操作（如 Conv → ReLU），通过共享内存或寄存器传递中间结果。

水平融合（Horizontal Fusion）

合并无数据依赖的独立kernel（如同时执行多个矩阵乘法，将多个shape较小的矩阵乘法合并成一个大的矩阵乘法），需统一线程组织结构（如调整Block/Grid尺寸）。

Double Buffer原理与实现

原理：
使用两块缓冲区交替进行数据加载和计算，隐藏内存传输延迟
CUDA实现：

cpp 复制代码

__shared__ float buffer0[BLOCK_SIZE];
__shared__ float buffer1[BLOCK_SIZE];
float* load_buf = buffer0;
float* compute_buf = buffer1;

for (int i = 0; i < iter; i++) {
    // 异步加载数据到 load_buf
    loadData(load_buf, i);

    __syncthreads();  // 等待加载完成

    // 处理 compute_buf 数据
    compute(compute_buf);

    // 交换缓冲区指针
    float* temp = load_buf;
    load_buf = compute_buf;
    compute_buf = temp;
}

CUDA常规知识点

👉 ThreadsPerBlock和Blocks的数量受哪些条件约束？

1. 硬件限制（上限）

(1) 线程与块维度约束

(2) SM 资源约束

2. 算法/问题需求（下限与结构）

👉 理论计算占用率公式

分量计算

关键说明

公式应用示例

👉 CUDA汇编-PTX与SASS

👉 浮点格式对比

👉 CUDA的内存模型

CUDA的内存模型Memory类型

Global memory的访存合并

寄存器(Register)与本地内存(Local Memory)的变量分配规则

👉 Bank Conflict 的优化方案

Bank Conflict 本质

避免方案（16种专业技巧）

👉 CUDA程序的调度和计算单元

Block在SM上的调度执行机制

CUDA Core vs Tensor Core

GPU分支预测与指令级并行

分支预测

指令级并行(ILP)

🫆分支发散（branch divergence）

有 if 的问题示例：

使用"掩码"用它代替 if

Float/Int指令周期与融合操作

指令延迟对比（Ampere架构）

融合操作示例

👉 Roofline模型及计算优化

Roofline Model 深度解析

模型核心要素

关键参数计算

优化决策树

典型场景优化策略

Kernel Fusion的优势与示例

核心原理与工作机制

核心优势

技术实现方式

Double Buffer原理与实现

有 `if` 的问题示例：

使用"掩码"用它代替 `if`