数据结构系列之链表

CAU界编程小白2025-09-24 15:10

前言

链表和顺序表是经常被拿出来对比的东西，就更要知道这两个的区别和如何使用,链表分为八种,带不带头(哨兵位的头结点),双不双向(C++里的list 和forward_list),循不循环(尾指针指向的是空,还是指向头结点,参考list中的begin和end迭代器)

本次实现双向带头循环和单向不带头不循环链表,这样所有的类型基本上都可以写出来了.

一、单向链表

单向链表没啥说的,一张图介绍一下

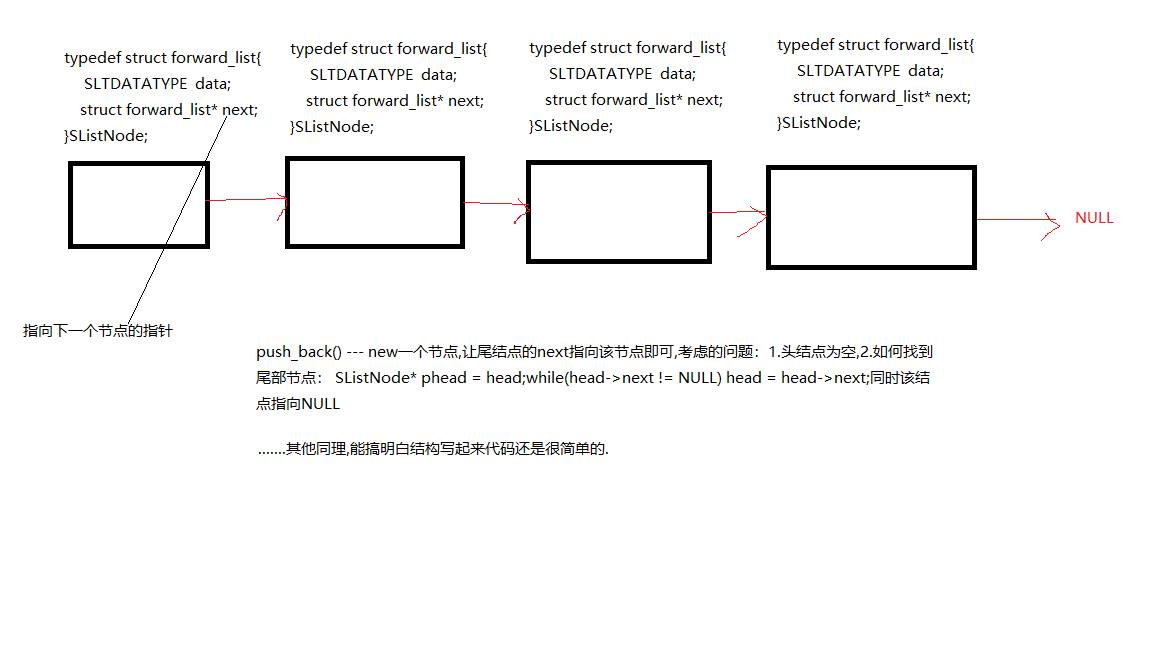
有一个问题关于二级指针的, 比如push_back(SListNode *head,SLTDATATYPE val) 这样对吗？当然不对,你可能会问,这本身就是指针为什么需要二级指针,为什么不对？因为当单链表是空的时候要修改头指针！所以这里要注意：1.使用二级指针，2：使用引用来玩

注意: 在pos后插入和pos前插入不需要二级指针,因为没有对指针本身进行修改,就不需要二级

如果有可能修改原来的指针，一定要用二级指针！！！

这里提到一下C++里的关于形参类型的标准

1.输入型参数 const xxx

2.输出型 * xxx

3.输入输出型 & xxxx

二、单链表的具体实现

c 复制代码 
#include<stdlib.h>
#include<string.h>
#include<assert.h>
#define SLTDATATYPE int
typedef struct SlistNode
{
	SLTDATATYPE data;
	struct SlistNode* next; 
	//SLTNode* next; //这种方式不行 因为得现有下面的名称SLTNode
	//SLT Single list 
}SLTNode;
void Print(SLTNode * pHead);
void SLPushBack(SLTNode** ppHead, SLTDATATYPE x);
void SLTPushFront(SLTNode** ppHead, SLTDATATYPE x);
SLTNode* BuySLTNode(SLTDATATYPE x);
//搞结点用的
void SLPopBack(SLTNode** ppHead);
void SLTPopFront(SLTNode** ppHead);
//查找-----也可以修改
SLTNode* SListFind(SLTNode* phead, SLTDATATYPE x); 
SLTNode* SListFind(SLTNode* phead, SLTDATATYPE x);
//pos之前插入
void SListInsert(SLTNode** ppHead,SLTNode* pos, SLTDATATYPE x);
//pos位置删除
void SListErase(SLTNode** ppHead,SLTNode* pos);
//pos后面插入
void SListInsertAfter(SLTNode* pos, SLTDATATYPE x);
//pos位置后面删除
void SListEraseAfter(SLTNode* pos);
void SLTDestroy(SLTNode** pHead);
void Print(SLTNode* pHead)
{
	//不需要断言 assert 本身就是空
	SLTNode* cur = pHead;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}

void SLTPushFront(SLTNode** ppHead, SLTDATATYPE x)
{
	SLTNode* newnode = BuySLTNode(x);
	newnode->next = *ppHead;
	*ppHead = newnode;
}
void SLPopBack(SLTNode** ppHead)
{
	assert(*ppHead!=NULL);
	if ((*ppHead)->next == NULL)
	{
		free(*ppHead);
		*ppHead = NULL; 
	}
	else
	{
		SLTNode* prev = NULL;
		SLTNode* tail = *ppHead;
		while (tail->next)
		{
			prev = tail;
			tail = tail->next;
		}
		free(tail);
		tail = NULL;
		prev->next = NULL;

	}
}

void SLTPopFront(SLTNode** ppHead)
{
	assert(*ppHead);
	SLTNode* first = *ppHead;
	*ppHead = first->next;
	free(first);
	first = NULL;

}
SLTNode* SListFind(SLTNode* phead, SLTDATATYPE x); 
SLTNode* SListFind(SLTNode* phead, SLTDATATYPE x)
{
	SLTNode* find = phead;
	while (find)
	{
		if (find->data == x)
		{
			return find;
		}
		find = find->next;

	}
	return NULL;
}
void SListInsert(SLTNode** ppHead, SLTNode* pos, SLTDATATYPE x)
{
	assert(ppHead);
	assert(pos);

	SLTNode* cur = *ppHead;
	if (pos == *ppHead)
	{
		SLTPushFront(ppHead, x);
	}
	else
	{
		while (cur->next != pos)
		{
			cur = cur->next;
		}
		SLTNode* newnode = BuySLTNode(x);
		cur->next = newnode;
		newnode->next = pos;
	}


}
//pos位置删除
//             pos 
//0->1->//2//->3->4->5
void SListErase(SLTNode** ppHead, SLTNode* pos)
{
	assert(pos);
	assert(ppHead);
	assert(*ppHead);
	SLTNode* cur = *ppHead;
	if (*ppHead == pos)
	{
		SLTPopFront(ppHead);
	}
	while (cur->next != pos)
	{
		cur = cur->next;
	}
	cur->next = pos->next;
	free(pos);
}
void SListInsertAfter(SLTNode* pos, SLTDATATYPE x)
{
	assert(pos);
	SLTNode* newNode = BuySLTNode(x);
	newNode->next = pos->next;
	pos->next = newNode;
}

//pos位置后面删除
void SListEraseAfter(SLTNode* pos)
{
	assert(pos);
	assert(pos->next);
	//pos->next = pos->next->next;//这样做不行
	SLTNode* del = pos->next;
	pos->next = pos->next->next;
	free(del);
	del = NULL;
     // pos 
} 

void SLPushBack(SLTNode** ppHead, SLTDATATYPE x)
{
	SLTNode * cur=BuySLTNode(x);

	//如果本身为空
	if (*ppHead == NULL)
	{
		*ppHead = cur;
	}
	else
	{
		SLTNode* tail = *ppHead;
		while (tail->next)
		{
			tail = tail->next;
		}
		tail->next = cur;
		cur->next = NULL;
    }
}
SLTNode* BuySLTNode(SLTDATATYPE x)
{
	SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
	if (newnode == NULL)
	{
		perror("malloc");
		return NULL;
	}
	newnode->next = NULL;
	newnode->data = x;
	return newnode;

}
void SLTDestroy(SLTNode** ppHead)
{
	SLTNode* cur = *ppHead;
	while (cur)
	{
		SLTNode* next = cur->next;
		free(cur);
		cur = next;
	}
	*ppHead = NULL;
}

数据结构作业

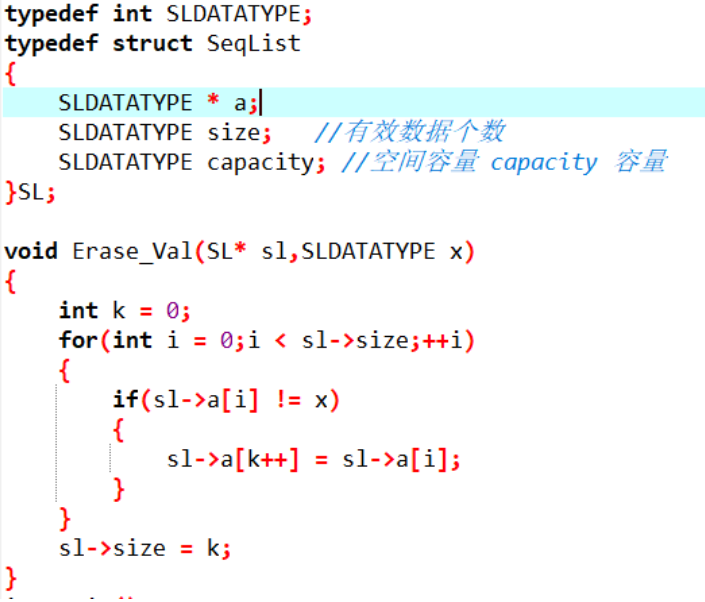
1.正好数据结构留了这个作业,就写一下，思路不是很难，遇到不是x的值直接从开始去覆盖即可.

2、定义三元组(a, b, c)（a、b、c均为正数）的距离D = |a - b| + |b - c| + |c - a|。给定3个非空整数集合S1、S2和S3，按升序分别存储在3个数组中。请设计一个尽可能高效的算法，计算并输出所有可能的三元组(a, b, c)（a ∈ S1, b ∈ S2, c ∈ S3)中的最小距离。例如 S1 = { -1, 0, 9}，S2 = {-25, -10, 10, 11}, S3 = {2, 9, 17, 30, 41}，则最小距离为2，相应的三元组为（9，10，9）。要求：

（1）给出算法的基本设计思想

（2）根据设计思想，采用C语言或C++语言描述算法，关键之处给出注释。

（3）说明你所设计算法的时间复杂度和空间复杂度。

思路和代码如下

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5;
int a[N], b[N], c[N];
// 思路：D = |a - b| + |b - c | + |c - a| -> D = 2 max(a,b,c) - min(a,b,c)

// 算法：用三指针来遍历
// 每次记录一个max和min,如果ans更小就更新,
// 每次移动最小的指针，因为是升序,这样才有可能更小，有一个停止就结束
// 因为要记录三元组,所以需要遍历两次
// 时间复杂度O(posa + posb + posc) 其中posa,posb,posc为三个数组中的长度
// 空间复杂度O(1) 不需要开额外空间
int main()
{
    int na, nb, nc;
    cin >> na >> nb >> nc;
    int posa = 0, posb = 0, posc = 0;
    for (int i = 0; i < na; ++i)
    {
        int x;cin >> x;
        if (x > 0) a[posa++] = x;
    }
    for (int i = 0; i < nb; ++i)
    {
        int x;cin >> x;     
        if (x > 0) b[posb++] = x;
    }
    for (int i = 0; i < nc; ++i)
    {
        int x;cin >> x;
        if (x > 0) c[posc++] = x;
    }
    int maxi = 0, mini = 0, ans = 1e9;
    int i = 0, j = 0, k = 0;
    while (i < posa && j < posb && k < posc)
    {
        int maxi = max(max(a[i], b[j]), c[k]);
        int mini = min(min(a[i], b[j]), c[k]);
        ans = min(ans, (maxi - mini) * 2);
        if (ans == 0)  {  break; }
        if (a[i] == mini) i++;
        else if (b[j] == mini) j++;
        else k++;
    }
    cout << "最小的D为" << ans << '\n';
    //输出三元组
    i = j = k = 0;
    while (i < posa && j < posb && k < posc)
    {
        int maxi = max(max(a[i], b[j]), c[k]);
        int mini = min(min(a[i], b[j]), c[k]);
        if(2 * (maxi - mini) == ans)
        {
            cout << "符合条件的三元组之一为" << a[i] << ',' << b[j] << ',' << c[k] << '\n';
        }
        if (a[i] == mini) i++;
        else if (b[j] == mini) j++;
        else k++;
    }
    return 0;
}

三、双向链表

其实和单向链表的差别不是很大,多了一个prev指针,来指向上一个结点，这里我画图画的是双向不带头循环链表

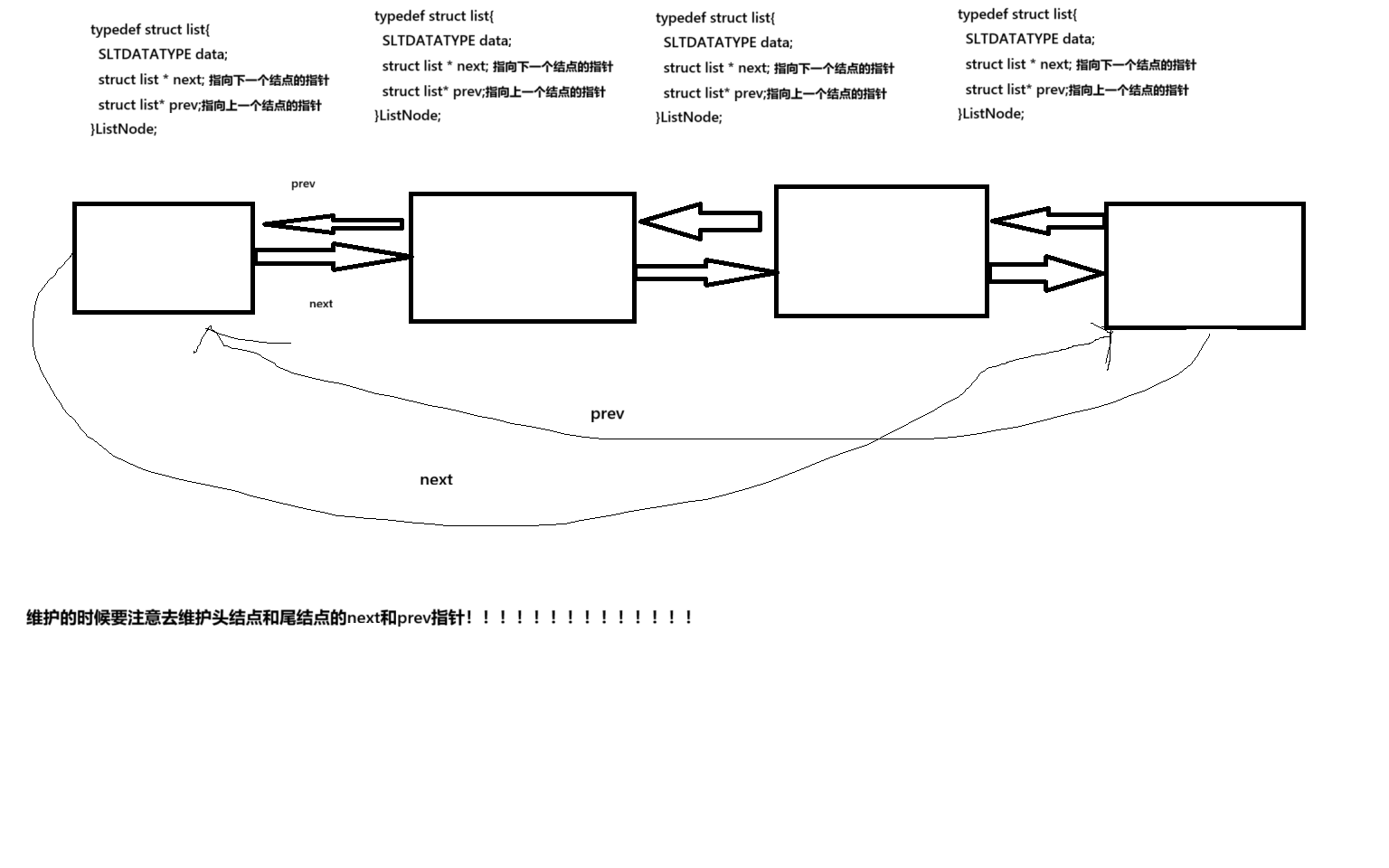
四、代码实现

我实现的是带头双向循环链表，带头的情况下一些函数就不需要传二级指针了。

既然带头了,就要控制好,头结点的next结点实际上才是真正的数据，记住这一点还是比较好维护的。也要记得维护next和prev指针，不要忘了某一个.

cpp 复制代码 
//链表--双向
#include <stdlib.h>//system //qsort //malloc
#include <stdio.h>//return 0
#include <assert.h>//assert 断言
#include<bits/stdc++.h>
typedef int LTDATATYPE;
typedef struct DlistNode
{
	struct DlistNode* next;
	struct DlistNode* prev;
	LTDATATYPE data;
}LTNode;

LTNode* LTInit();
//可以传二级指针，也可以用返回值去接受
void Destory(LTNode* phead);
void LTPushback(LTNode* phead, LTDATATYPE x);
void LTPopback(LTNode* phead, LTDATATYPE x);
LTNode *BuyListnode(LTDATATYPE x);
void LTPrint(LTNode* phead);
bool LTEmpty(LTNode* phead);
void LTPushfront(LTNode* phead, LTDATATYPE x);
void LTPopfront(LTNode* phead);
void LTErase(LTNode* pos);
void LTInsert(LTNode* pos, LTDATATYPE x);
LTNode* find(LTNode* phead, LTDATATYPE x);
LTNode* LTInit()//**ppHead
{
	LTNode * head = BuyListnode(-1);
	head->next = head;
	head->prev = head;
	return head;
}
void LTPrint(LTNode* phead)
{
	assert(phead);
	LTNode* cur = phead->next;
	printf("<=head=>");
	while (cur != phead)
	{
		printf("%d <=>", cur->data);
		cur = cur->next;
	}
}
LTNode *BuyListnode(LTDATATYPE x)
{
	LTNode* node =(LTNode*) malloc(sizeof(LTNode));
	if (node == NULL)
	{
		perror("malloc");
		return NULL;
	}

	node->next = NULL;
	node->prev = NULL;
	node->data = x;
	return node;
}
void Destory(LTNode* phead)
{
	assert(phead);
	LTNode* cur = phead;
	while (cur != phead)
	{
		LTNode* next = cur->next;
		free(cur);
		cur = next;
	}
	free(phead);
	phead = NULL;
}
void LTPushback(LTNode* phead, LTDATATYPE x)
{
	assert(phead);
	LTNode* newnode = BuyListnode(x);
	LTNode* tail = phead->prev;
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next =phead;
	phead->prev = newnode;
}
bool LTEmpty(LTNode* phead)
{
	assert(phead);
	return phead->next == phead;
}
//phead    tailprev  tail 
void LTPopback(LTNode* phead, LTDATATYPE x)
{
	assert(phead);
	assert(!LTEmpty(phead));
	LTNode* tail = phead->prev;
	LTNode* tailprev = tail->prev;
	tailprev->next = phead;
	phead->prev = tailprev;
	free(tail);
	tail = NULL;
}
//phead node p1
void LTPushfront(LTNode* phead, LTDATATYPE x)
{
	assert(phead);
	LTNode* node = BuyListnode(x);
	node->next = phead->next;
	phead->next->prev = node;
	phead->next = node;
	node->prev = phead;
}
//head next
//head  1    2    3    4    5
void LTPopfront(LTNode* phead)
{

	assert(phead);
	assert(!LTEmpty(phead));
	LTNode* next = phead->next;
	phead->next = next->next;
	next->next->prev = phead;
}
      //pos
//head 1 2 3 
void LTErase(LTNode* pos)
{
	assert(pos);
	LTNode* prev = pos->prev;
	LTNode* next = pos->next;
	prev->next = next;
	next->prev = prev;
	free(pos);
	pos = NULL; //形参的改变不影响实参，给pos置空没有意义
}//       pos  
//head 1 2 3 pos 4 5 
 //pos newnode next
//head 1 2 3 4 5
void LTInsert(LTNode* pos, LTDATATYPE x)
{
	LTNode* newnode = BuyListnode(x);
	LTNode * next = pos->next;
 //pos  newnode next 
	pos->next = newnode;
	newnode->prev = pos;
	newnode->next = next;
	next->prev = newnode;
}
LTNode* find(LTNode* phead, LTDATATYPE x)
{

	LTNode *find = phead->next;
	while (find != phead)
	{
		if (find->data == x)
		{
			return find;
		}
		find = find->next;
	}
	return NULL;
}

总结

下次应该是栈和队列

相关推荐
深思慎考6 小时前
LinuxC++项目开发日志——基于正倒排索引的boost搜索引擎（3——通过cppjieba库建立索引模块）
linux·c++·搜索引擎
Onesoft%J1ao6 小时前
C++ 1.STL-vector 2.STL-list 3.数组模拟单向链表 详解配例题 通俗易懂
c++·青少年编程·list
_OP_CHEN6 小时前
数据结构（C语言篇）：（十六）插入排序
c语言·数据结构·排序算法·学习笔记·插入排序·希尔排序·直接插入排序
理论最高的吻7 小时前
108. 将有序数组转换为二叉搜索树【 力扣(LeetCode) 】
c++·算法·leetcode·职场和发展·二分查找·平衡二叉树
感哥1 天前
C++ 三之法则、五之法则和零之法则
c++
感哥2 天前
C++ 迭代器
c++
tkevinjd3 天前
C++线程池学习 Day07
c++
TangHao19873 天前
第一章 基础（Chapter 1 fundentals）
c++
沐怡旸3 天前
【底层机制】std::move 解决的痛点？是什么？如何实现？如何正确用？
c++·面试
热门推荐
01UV 工具安装与国内镜像源配置指南02Spec-Kit 使用指南03GitHub 镜像站点0446个Nano-banana 精选提示词，持续更新中05UV安装并设置国内源06保姆级教程：手把手教你用Dify实现完美多轮对话（附Chatflow和提示词）07解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题08KGG转MP3工具|非KGM文件|解密音频09Linux下V2Ray安装配置指南10jdk21下载、安装（Windows、Linux、macOS）